摩擦系数对滚动接触疲劳裂纹萌生和磨耗影响
2018-11-02韩延彬木东升黄旭炜
周 宇, 韩延彬, 木东升, 黄旭炜
(同济大学 道路与交通工程教育部重点实验室,上海 201804)
钢轨表面的滚动接触疲劳裂纹和磨耗是影响钢轨寿命的主要伤损[1],轮轨间的摩擦系数对轮轨力有明显的影响[2],Li Zili等[3]分析了摩擦系数对钢轨材料塑性变形和压陷型伤损形成的影响.邓铁松等[4]分析了不同摩擦因数对疲劳裂纹萌生寿命、萌生位置和启裂角度的影响.肖乾等[5]分析了摩擦系数对车轮接触斑疲劳指数和车轮伤损分布的影响.更多文献对摩擦系数的研究则是针对裂纹扩展阶段的裂纹尖端应力强度因子[6]、扩展路径变化[7]等开展.而钢轨疲劳裂纹和磨耗是同时存在、共同发展、相互影响的,考虑轮轨间的摩擦系数对钢轨这2种伤损相互作用机制情况下的影响程度,特别是曲线外轨轨距角裂纹和内轨顶面裂纹萌生与两轨磨耗之间的关系,对于调节轮轨摩擦系数、减缓钢轨疲劳伤损,延长钢轨表面疲劳裂纹萌生寿命和磨耗寿命非常重要.
基于临界平面法材料疲劳损伤理论和Archard磨耗理论,建立三维钢轨裂纹萌生和磨耗发展共存预测模型,分析不同轮轨摩擦系数条件下曲线外轨和内轨的钢轨表面疲劳裂纹萌生寿命、萌生位置以及裂纹萌生时的磨耗量、磨耗发展率,量化轮轨摩擦系数对疲劳裂纹萌生和磨耗共存发展的影响,为合理的摩擦系数管理和调节提供依据.
1 裂纹萌生和磨耗共存发展预测模型
1.1 疲劳裂纹萌生与磨耗共存发展离散化过程建模
钢轨疲劳裂纹和磨耗是一个同时存在、共同发展、相互影响的连续过程[1,8],为了将这一连续过程用数学方法描述和建模,首先认为这个疲劳裂纹和磨耗的连续发展过程是大量车轮作用的结果,假设每一个车轮作用在一段钢轨上都会引起该段钢轨材料的疲劳损伤累积、磨耗并引起钢轨型面的变化.那么疲劳裂纹萌生和磨耗的连续发展过程就可以离散成有限个车轮作用在钢轨上引起材料疲劳累积、磨耗和钢轨型面变化、直至疲劳裂纹萌生的过程.
这样,当一个车轮通过某段钢轨时,轮轨接触状态引起钢轨产生应力应变,导致材料疲劳损伤和磨损;该车轮通过后下一个车轮通过前,钢轨材料疲劳损伤发生累积,同时型面因磨耗而发生变化,成为磨耗型面;下一个车轮作用在这个磨耗型面时,发生新的轮轨接触状态,又引起新的钢轨应力应变、材料疲劳损伤和累积、磨损和型面变化.这就将钢轨疲劳裂纹萌生和磨耗共存发展的连续过程离散为每个车轮作用结果的组合,可由图1示意.
从图1可以看出,针对钢轨疲劳裂纹萌生这个阶段,将裂纹萌生和磨耗共存发展的连续过程离散化,每个离散化的阶段由2个主要的子阶段组成,分别是①疲劳-磨耗单独发展子阶段;②磨耗型面替换-疲劳累积子阶段.在疲劳-磨耗单独发展子阶段,钢轨型面不变化,磨耗和疲劳分别单独计算,即一方面根据磨耗模型计算单次车轮通过时引起的轨头接触区的磨耗量,但不替换钢轨型面,另一方面,计算钢轨型面不变情况下钢轨轨头任意点的疲劳损伤寿命,并得到单次车轮作用下的单次疲劳损伤;之后,进入磨耗型面替换-疲劳累积子阶段,将单次车轮引起的磨耗量叠加到钢轨型面上,计算型面接触区的磨耗分布并平滑型面,得到磨耗型面,并替换掉上一阶段的钢轨型面,同时,将疲劳损伤累积;接下来又进入新的疲劳-磨耗单独发展子阶段,但在这个阶段钢轨型面已经替换成了上一子阶段得到的磨耗型面,轮轨接触和由此引起的应力应变、疲劳累积、磨耗位置和磨耗量相应都发生变化,如此循环直到钢轨疲劳累积损伤达到临界值,则钢轨疲劳裂纹萌生.

图1 钢轨疲劳裂纹萌生和磨耗共存发展过程的离散化
Fig.1Discretizationofthecoexistenceprocessoffatiguecrackinitiationandweargrowth
这样,将每个车轮作用下的裂纹萌生-磨耗共存发展过程离散成钢轨疲劳-磨耗单独发展子阶段和磨耗型面替换-疲劳累积子阶段,既可以认为逼近了裂纹萌生-磨耗共存发展的连续过程,又可以实现数学描述和建模.
考虑到离散成每个车轮作用在钢轨上时的仿真过程非常耗时,也可以将上述离散过程按照一定的累积磨耗量(即累积一定通过车轮次数)分段,整个裂纹萌生-磨耗共存的过程仍然分为有限个车轮通过次数积累的磨耗-疲劳单独累积子阶段,以及瞬时完成磨耗型面替换和疲劳累积的磨耗型面替换-疲劳累积子阶段,直至疲劳到限,裂纹萌生.这样,可以在疲劳-磨耗单独累积子阶段分别计算磨耗量和疲劳损伤,当钢轨轨头任意点的最大磨耗量达到设定值时,仿真进入磨耗型面替换-疲劳累积阶段,同时累积车轮通过次数、计算总磨耗量和磨耗型面、替换磨耗型面并进行不同离散阶段间的疲劳累积,如图2所示[9].图2a~2d分别是每个磨耗型面对应的轨头内若干点的疲劳累积情况,其中R0(实线)表示标准型面,Ri(虚线,i=1,2,3,…,i,下同)表示第i次替换的磨耗型面.轨面下的黑色点表示荷载作用下轨头材料中疲劳累积较大的点,其中A点为疲劳累积最快到达临界疲劳损伤的点,该点在每个磨耗型面时对应的萌生寿命为Nfi(即型面不变情况下达到疲劳损伤时车轮通过次数),实际上每个型面发生磨耗被替换时对应的车轮通过次数为ni.因此,每个磨耗型面时A点的疲劳伤损为Di=ni/Nfi.

a n1
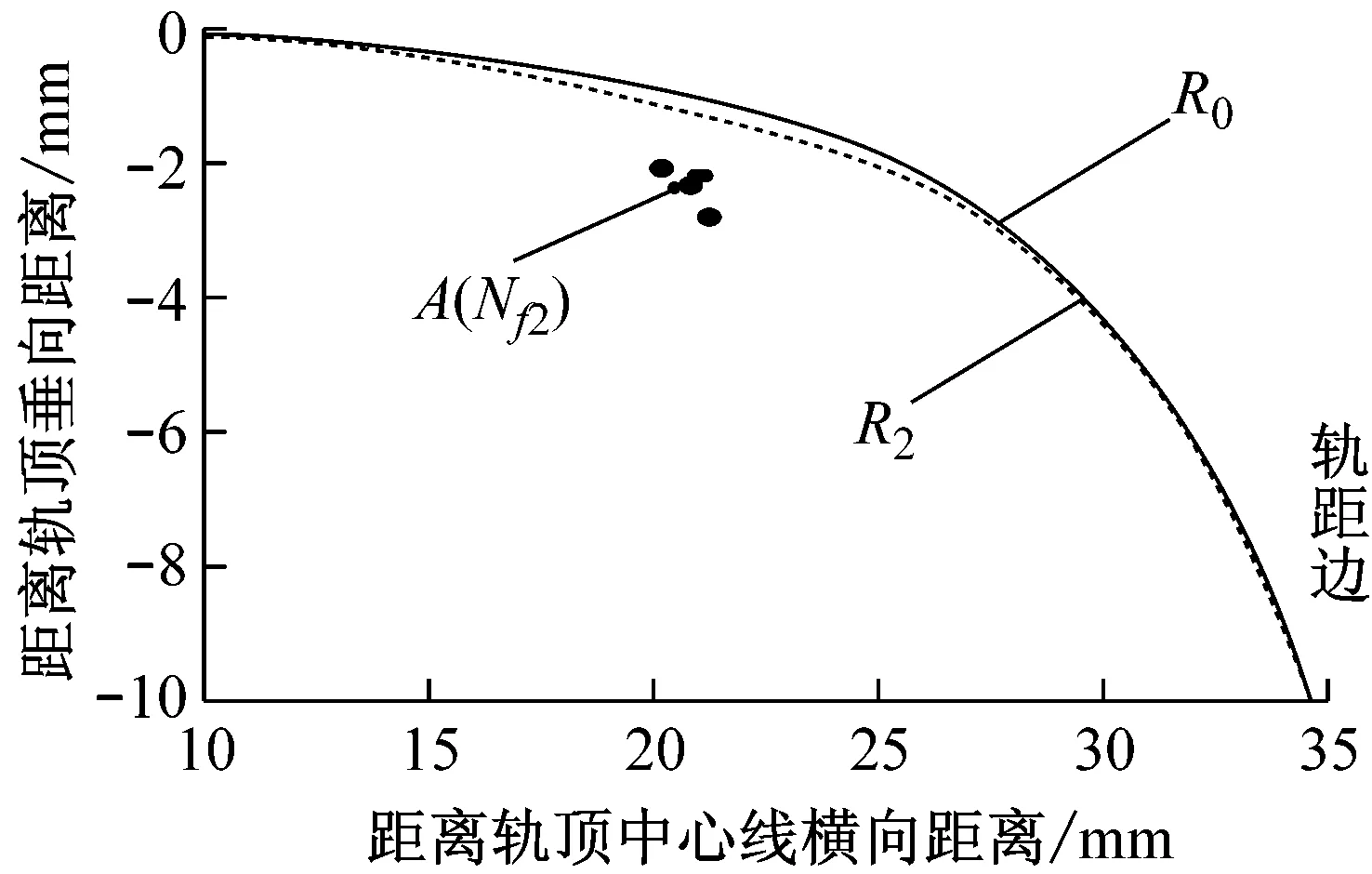
b n2

c n3

d ni
Fig.2Predictionprocedureofthecoexistenceoffatiguecrackinitiationandweargrowth
1.2 疲劳裂纹萌生与磨耗共存发展预测模型
根据疲劳裂纹萌生与磨耗共存发展建模设想,建立疲劳裂纹萌生与磨耗共存发展预测仿真流程如图3所示.图3中zni表示在车轮第n次通过时,第i个磨耗型面时引起的钢轨磨耗深度;Σzni表示车轮通过n次、第i个磨耗型面时的钢轨磨耗累积深度;Fpmax表示钢轨轨头材料的疲劳参量最大值.
从图3可以看出,要实现疲劳裂纹萌生与磨耗共存发展建模设想,2个子阶段分别需要轮轨接触计算、磨耗计算、疲劳损伤计算、磨耗型面替换和疲劳累积等5个关键步骤.
1.2.1疲劳-磨耗单独发展子阶段
(1)轮轨接触计算.轮轨接触斑计算获得钢轨接触斑蠕滑状况和法向力、切向力分布.首先,采用多体动力学软件Simpack计算轮轨力、接触斑形状和位置、蠕滑状况等参数;采用轮轨接触软件CONTACT计算轮轨接触应力和切向应力及其分布;然后,建立长钢轨三维有限元全局模型,计算钢轨位移约束条件;其次,把全局模型中单个车轮作用下的接触斑及其附近一定范围的钢轨细化网格,形成钢轨子模型,在轮轨接触位置施加垂向和切向应力分布,计算轨头内部各节点的应力应变状态.如图4所示.
(2)钢轨磨耗计算.根据Archard磨耗理论,有
(1)
式中:Vm为材料磨耗体积;D为滑动距离;T为轮轨法向力;H为材料的硬度;K为磨耗系数,由滑动距离和法向压力决定[10].K值取各区域磨耗系数平均值[10-11].当考虑接触斑面积及接触斑的黏着区/滑动区分布且认为只有滑动区引起磨耗,式(1)中的N由接触应力代替,则可以计算出接触斑内滑动区任意点的磨耗量,即磨耗深度.
对于一个车轮来说,钢轨表面某点的磨耗是由该车轮在不同时刻碾压该点的所有接触斑滑动区引起,而该车轮在不同时刻的接触斑与该点的相对位置不同,为计算一个车轮滚过某点的等效磨耗效应,假设轮轨接触为稳态形式,即不同时刻接触斑上的接触应力、蠕滑率、蠕滑力、接触斑面积、黏着区/滑动区等保持不变.当一个车轮滚过时,钢轨表面某点的磨耗量等效于该车轮不同时刻的接触斑滑动区前缘向后沿纵向直线方向移动至接触斑滑动区后缘引起的累积磨耗量.例如图5中一个车轮引起的接触斑对轨头某点(通过接触斑中心的O点)的磨耗量为经过该点的接触斑滑动区内纵向黑色条带所引起(图5中阴影单元格为接触斑滑动区范围)[12].
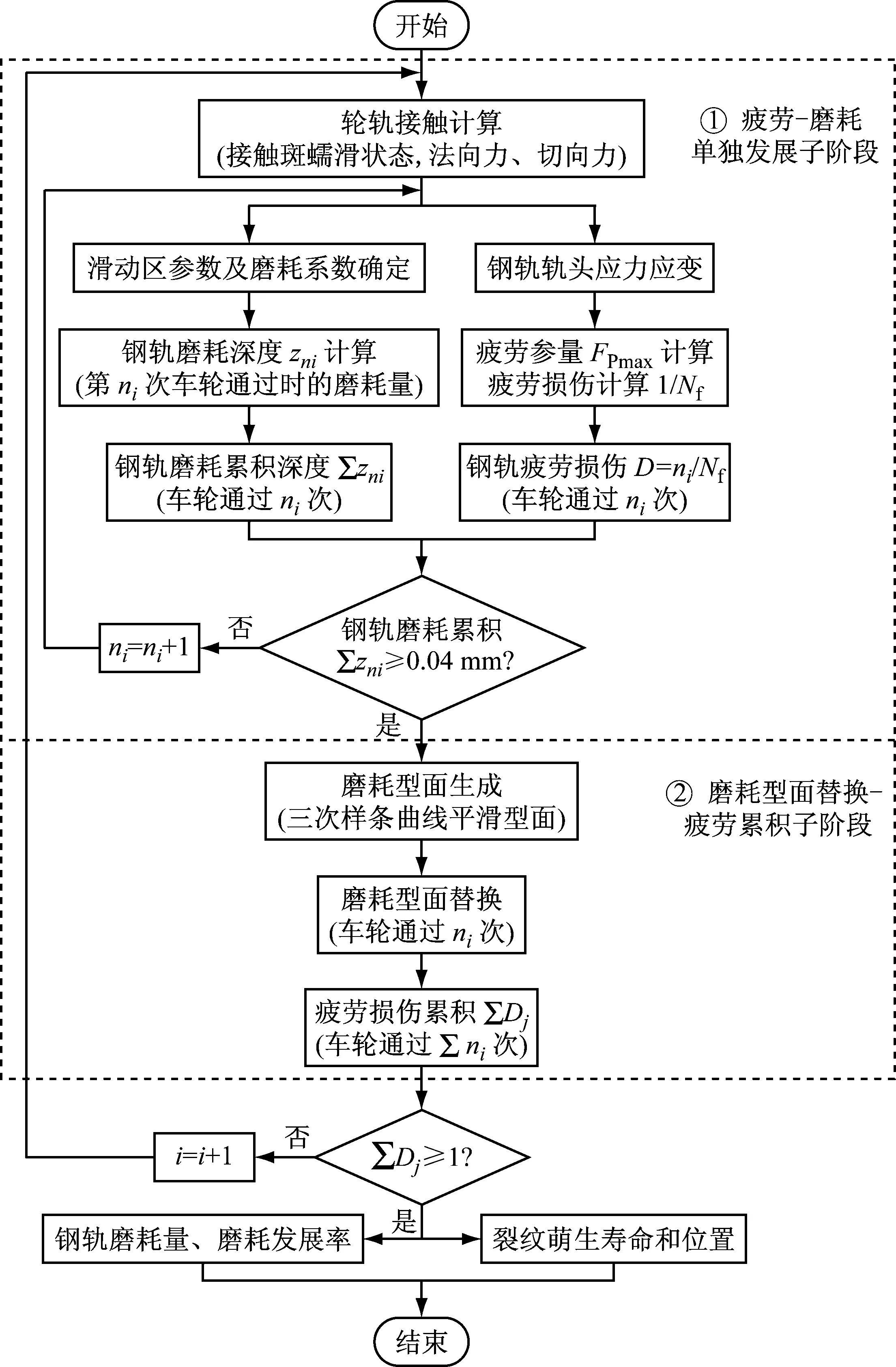
图3 疲劳裂纹萌生与磨耗共存发展离散化仿真计算流程

图4 钢轨有限元模型
因此,当4个车轮通过时,钢轨表面接触斑内任意点的等效磨耗量为
(2)
式中:Δzy为接触斑在横坐标为y时的纵向阴影单元格的磨耗量;Δz(x,y)为单元格(x,y)处的磨耗量;m为接触斑纵向单元格数量;l为接触斑横向单元格数量.

图5 接触斑通过钢轨某点磨耗累积计算
(3)钢轨疲劳损伤计算和裂纹萌生寿命预测.对于每一个型面,其对应的疲劳损伤根据临界平面法和能量密度法得到,其中疲劳参量为[9,12-14]
(3)
式中:〈〉为MacCauley括号,〈σmax〉=0.5(|σmax|+σmax),σmax为裂纹面上的最大正应力;Δε为裂纹面上正应变幅值;Δτ和Δγ分别为裂纹面上剪应力幅值和剪应变幅值;J为材料参数.
将轨头各点的应力应变输入式(3)中,计算得到轨头任意点的疲劳参量,找到最大疲劳参量FPmax及其所在点;由最大疲劳参量,考虑正应力和剪应力的关系,采用式(4)可以计算出每个磨耗型面不变时任意点j对应的裂纹萌生寿命Nfij以及单个车轮作用下的单次疲劳损伤1/Nfij.
(4)
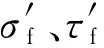
1.2.2磨耗型面替换-疲劳累积子阶段
(1)磨耗型面替换.根据式(2)计算1节车辆分别作用在2股钢轨上的4个车轮的接触斑所引起的钢轨磨耗量.当轨头任意点累积磨耗量达到一定数值时(本文为0.04 mm),将接触斑滑动区范围内的累积磨耗量叠加到钢轨型面上,并用三次插值样条曲线进行型面平滑[11],得到磨耗型面,同时得到型面替换时阶段累积车轮通过次数ni.
(2)疲劳累积.根据ni与Nfi,可得到该磨耗阶段对应的阶段疲劳损伤为
Di=ni/Nfi
(5)
根据Miner法则,当钢轨轨头任意点在不同磨耗阶段的疲劳损伤累积达到临界疲劳损伤,即
∑Di=D1+D2+D3+…+Di=1
(6)
此时认为该点萌生疲劳裂纹.其萌生寿命为
(7)
式中:N为钢轨疲劳裂纹萌生寿命;M为磨耗型面的替换次数,即裂纹萌生-磨耗共存离散化的次数.
2 仿真条件
根据上述疲劳裂纹萌生与磨耗共存发展预测模型,按表1车辆、轨道条件进行仿真,其中摩擦系数为轮轨接触位置的摩擦系数,分别为0.1、0.2、0.3、0.4、0.5、0.6、0.7.对于曲线外轨,轮轨接触主要分布在轨距角-轨肩,对于曲线内轨,轮轨接触主要分布在钢轨顶面.摩擦系数的取值范围从较光滑情况的0.1、0.2至较粗糙情况的0.6、0.7,内外轨摩擦系数相同.

表1 车辆和轨道主要参数
3 结果分析
3.1 摩擦系数对轮轨接触的影响
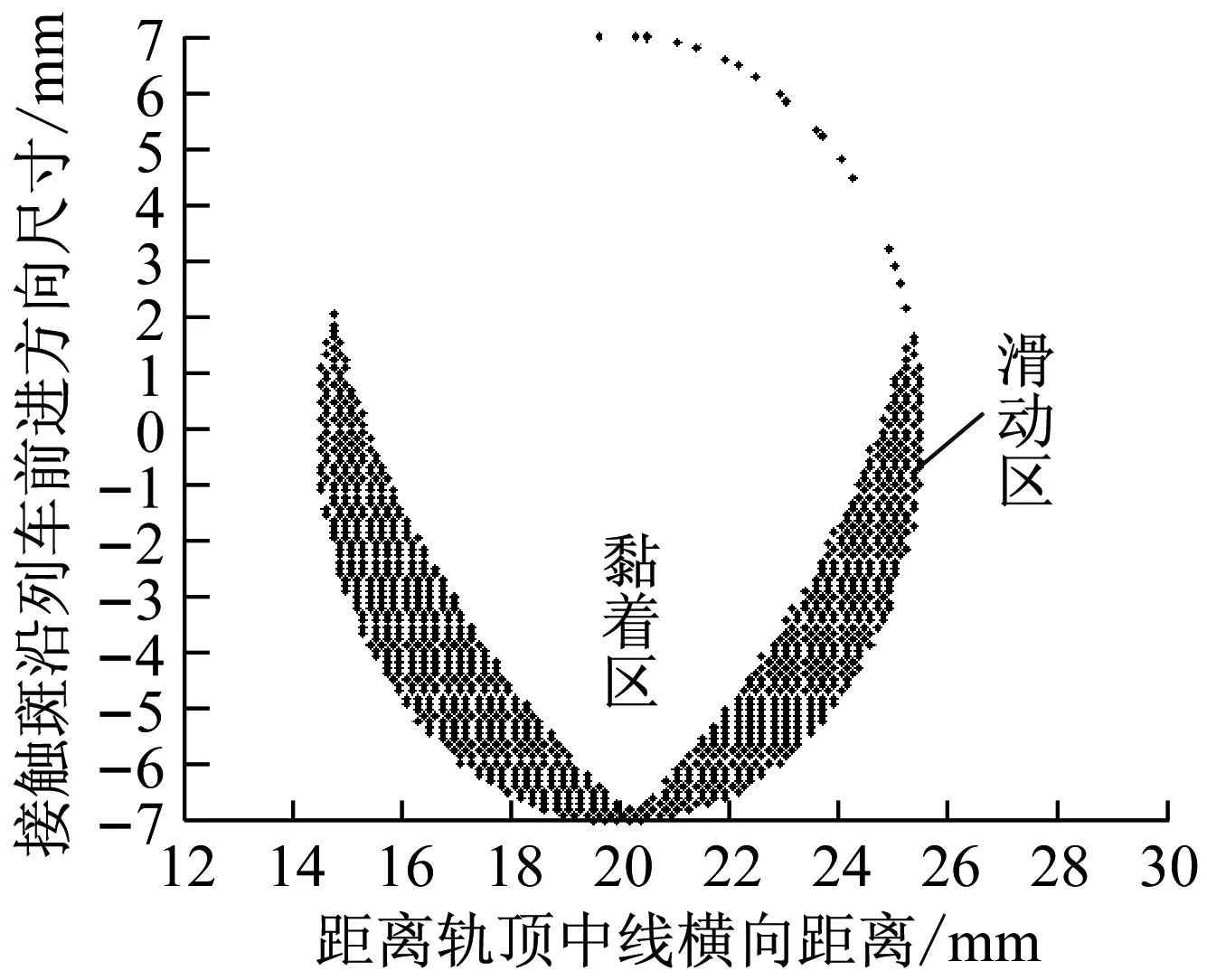
在4种摩擦系数工况下,前转向架第1个轮对外侧车轮所引起的接触斑在钢轨上的位置及黏着区/滑动区分布如图6所示,其中μ为摩擦系数.
从图6可知,4种摩擦系数下前转向架第1个轮对外侧车轮的接触斑形状与接触位置变化微小,但是接触斑黏着区/滑动区的分布有所不同,黏着区面积随着摩擦系数的增大而增加,滑动区的变化趋势则相反.在不同摩擦系数工况下,接触斑上的应力分布情况如图7所示.
由图7可知,随着摩擦系数的增大,作用于钢轨上的法向应力基本保持不变,接触区纵向切应力和横向切应力有增大的趋势.摩擦系数由0.3增大至0.5、0.7时,接触斑内的纵向切应力分别增大约20%、80%,横向切应力均增大约30%.
3.2 摩擦系数对磨耗的影响
阶段磨耗发展率是指在每一个疲劳-磨耗单独发展子阶段,从钢轨第i个磨耗型面上任意点的累积磨耗量达到规定值(本文为0.04 mm)时,每万次车轮通过时产生的磨耗量.平均磨耗发展率为裂纹萌生时所有阶段磨耗发展率平均值.其中,曲线内轨在摩擦系数为0.1时的裂纹萌生寿命无穷大,故内轨在摩擦系数为0.1的工况下不进行分析.不同摩擦系数下曲线外轨从原始型面到裂纹萌生时的阶段磨耗发展率如图8所示.

b μ=0.3

c μ=0.4
d μ=0.5
由图8可知:
(1)在不同摩擦系数下,外轨至裂纹萌生前发生了5次磨耗型面的替换过程,总磨耗量约为0.14~0.18 mm.

a 摩擦系数0.2,法向应力
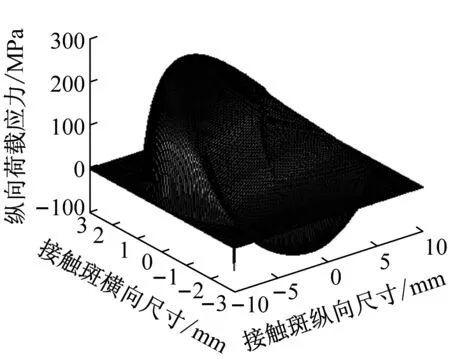
b 摩擦系数0.2,切向应力(纵向)

c 摩擦系数0.2,切向应力(横向)

d 摩擦系数0.3,法向应力

e 摩擦系数0.3,切向应力(纵向)

f 摩擦系数0.3,切向应力(横向)

g 摩擦系数0.4,法向应力

h 摩擦系数0.4,切向应力(纵向)

i 摩擦系数0.4,切向应力(横向)

j 摩擦系数0.5,法向应力

k 摩擦系数0.5,切向应力(纵向)

l 摩擦系数0.5,切向应力(横向)

m 摩擦系数0.7,法向应力

n 摩擦系数0.7,切向应力(纵向)

o 摩擦系数0.7,切向应力(横向)

图8不同摩擦系数下外轨的磨耗发展率随车轮通过次数的发展情况
Fig.8Developmentofweargrowthrateofhighrailbythewheelscycleaccumulationwithdifferentfrictioncoefficient
(2)随着车轮累积通过次数即通过总重的增加,不同摩擦系数下外轨的磨耗发展率整体上均呈现降低的趋势,说明无论在任何摩擦系数下,钢轨的磨耗使得轮轨型面匹配改善,轮轨关系趋向于良好,但是由于磨耗发展率仍为正值,钢轨累积磨耗量仍然不可避免呈现增加趋势.
(3)摩擦系数在0.1~0.2时,磨耗发展率随着车轮通过次数累积呈降低趋势且降速较平缓,2次磨耗型面替换之间的车轮通过次数较多;摩擦系数在0.3~0.7时,磨耗发展率随着车轮通过次数累积呈降低趋势且降速较快,2次磨耗型面替换之间的车轮通过次数较少,即摩擦系数大,磨耗速率变化快、磨耗增加快,车轮通过次数累积就少.
此外,内轨磨耗发展率随车轮通过次数的发展趋势与外轨相同,在裂纹萌生前同样发生了5次磨耗型面的替换,裂纹萌生时的磨耗量约为0.16~0.18 mm,但在同一摩擦系数下,内轨裂纹萌生时的车轮通过次数约为外轨的1.8~2.0倍,即内轨裂纹萌生寿命较外轨长.
在不同摩擦系数下,裂纹萌生时曲线外轨和内轨的平均磨耗发展率如图9所示,其中平均磨耗发展率按二次多项式进行拟合.

图9 不同摩擦系数下的钢轨平均磨耗发展率
Fig.9Averageweargrowthrateofrailswithdifferentfrictioncoefficient
从图9中可以看出,
(1)随着摩擦系数的增大,内轨、外轨的至裂纹萌生时的平均磨耗发展率均呈增大趋势,其中外轨平均磨耗发展率增幅较大.
(2)摩擦系数为0.3时,外轨平均磨耗发展率为2.32 μm·(104次)-1;摩擦系数为0.4时,其平均磨耗发展率为2.72 μm·(104次)-1,比摩擦系数为0.3时增大约17%,摩擦系数为0.5、0.6、0.7时的平均磨耗发展率分别相对摩擦系数为0.3时增大约26%、42%、55%.
(3)摩擦系数为0.3时,内轨平均磨耗发展率为1.92 μm·(104次)-1;摩擦系数为0.4时,其平均磨耗发展率为2.24 μm·(104次)-1,比摩擦系数为0.3时增大约16%,摩擦系数为0.5、0.6、0.7时的平均磨耗发展率分别相对摩擦系数为0.3时增大约29%、38%、42%.
3.3 摩擦系数对裂纹萌生的影响
在不同摩擦系数下,内、外轨的疲劳裂纹萌生寿命如图10所示,其中车轮通过次数按照表1的轴重进一步统计为通过总质量.此外,根据不同摩擦系数下的内、外轨裂纹萌生寿命,按二次多项式进行拟合.
从图10中可以看出:
(1)随着摩擦系数的增大,外轨和内轨的裂纹萌生寿命均减小,且内轨疲劳裂纹萌生寿命减小趋势较外轨明显,说明曲线段内轨裂纹萌生寿命对摩擦系数的变化更为敏感.
(2)摩擦系数为0.3时,外轨的裂纹萌生寿命为3.86×105次车轮通过次数,对应的通过总质量约为6.95×106t;摩擦系数为0.4时,外轨的裂纹萌生寿命为2.94×105次车轮通过次数,对应的通过总质量约为5.29×106t,比摩擦系数为0.3时减小约24%.摩擦系数为0.5、0.6、0.7时的裂纹萌生寿命分别相对摩擦系数为0.3时减小约26%、31%、34%.
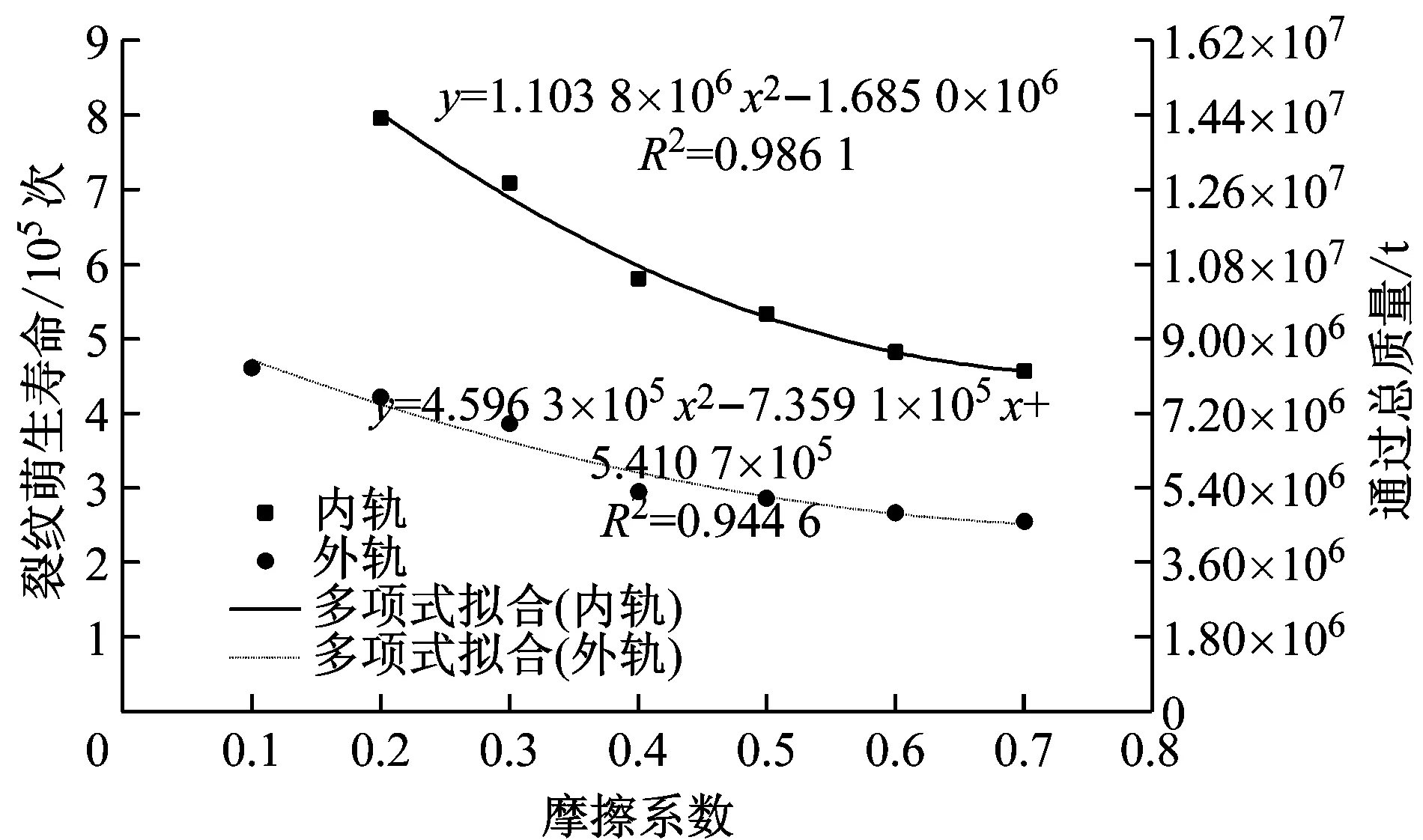
图10 裂纹萌生寿命与摩擦系数的关系
(3)摩擦系数为0.3时,内轨的裂纹萌生寿命为7.09×105次车轮通过次数,对应的通过总质量约为1.28×107t;摩擦系数为0.4时,内轨的裂纹萌生寿命为5.81×105次车轮通过次数,对应的通过总质量约为1.05×107t,比摩擦系数为0.3时减小约18%.摩擦系数为0.5、0.6、0.7时的裂纹萌生寿命分别相对摩擦系数为0.3时减小约25%、32%、35%.
不同摩擦系数下曲线内、外轨疲劳裂纹萌生位置如图11所示.
由图11可知,在同样的车辆和线路条件下,不同摩擦系数下的疲劳裂纹萌生于钢轨表面或亚表面的同一局部范围内,且摩擦系数增大,外轨的裂纹萌生位置向钢轨表面移动.进一步,不同摩擦系数下内轨和外轨的裂纹萌生点分布位置如图12所示.
由图12可知:
(1)在不同摩擦系数情况下,外轨疲劳裂纹萌生位置分布在靠近轨肩-轨距角一侧、距离轨顶中线17~18 mm、轨顶面下0.9~2.5 mm的局部区域.
(2)在不同摩擦系数情况下,内轨疲劳裂纹萌生位置分布在靠近轨肩-轨距角一侧距离轨面中线10~11 mm、轨顶面下2.4~2.6 mm的局部区域.内轨裂纹萌生位置相对于外轨更靠近轨面中线,垂向位置更靠下,这与现场观测情况吻合[8].
(3)当摩擦系数小于0.3时,外轨裂纹萌生点垂向位置在轨面以下2.1~2.4 mm,当摩擦系数大于0.3时,裂纹萌生点垂向位置在轨面以下0.9~1.0 mm,更靠近轨顶面.

a 外轨裂纹萌生位置

b 外轨裂纹萌生位置(二维)

c 外轨裂纹萌生深度(图b局部放大)
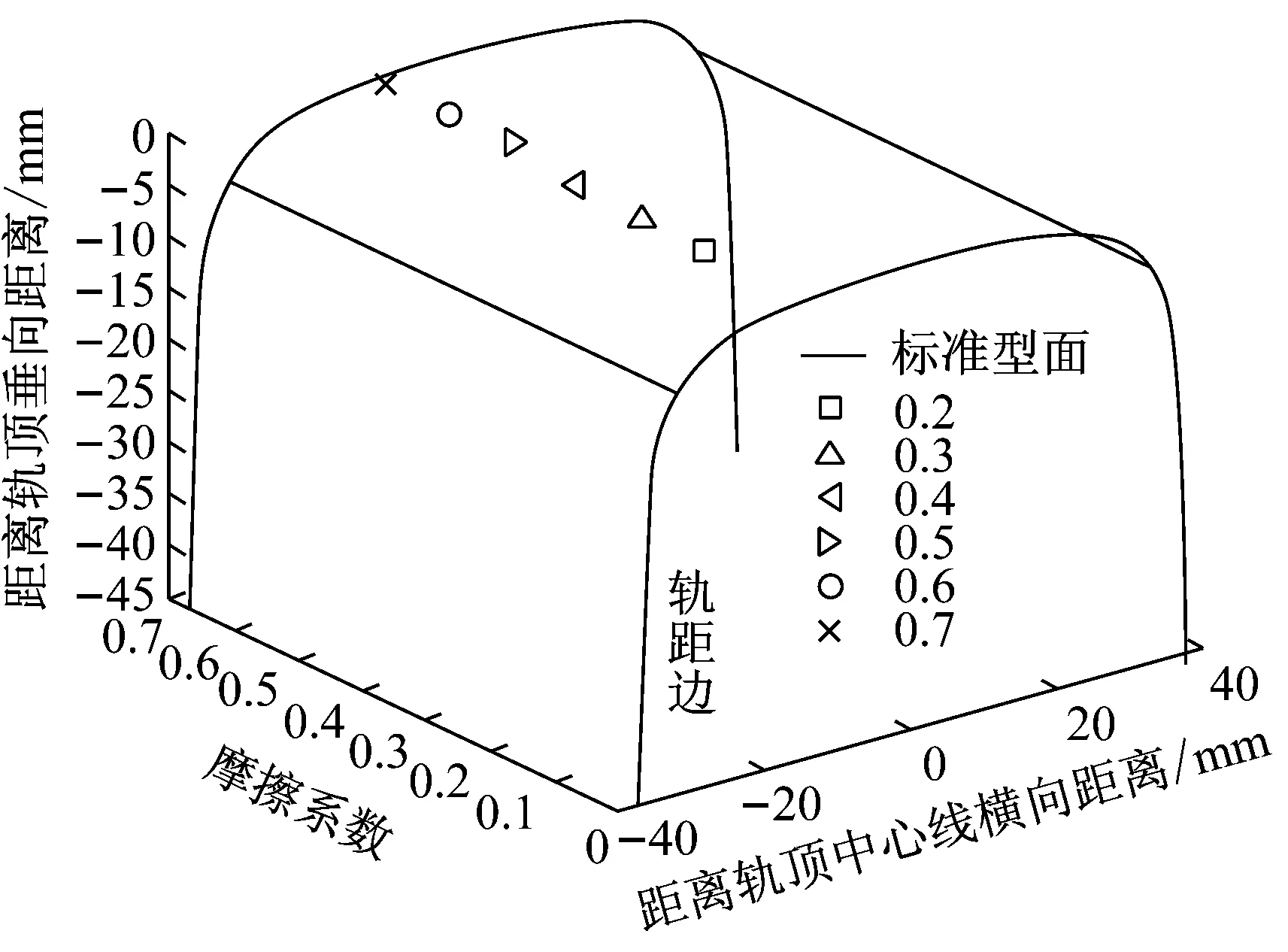
d 内轨裂纹萌生位置

e 内轨裂纹萌生位置(二维)

f 内轨裂纹萌生深度(图e局部放大)
(4)当摩擦系数在0.2~0.7时,内轨裂纹萌生点垂向位置始终在轨面以下2.4~2.6 mm.
3.4 摩擦系数对裂纹萌生和磨耗共存的影响
将图9、图10综合分析,如图13所示.值得注意的是,图13中纵向坐标轴裂纹萌生寿命和平均磨耗发展率并无对应关系,两者单位和含义不同,因此图中趋势线的交点并无含义,将裂纹萌生寿命和磨耗发展率放在同一图表中仅仅是便于直观对比分析.
从图13及前几节分析看出:
(1)当摩擦系数在0.1~0.2之间时,外轨裂纹萌生寿命约为4.22×105~4.61×105次,对应通过总质量约为7.72×106~8.43×106t,平均磨耗发展率约为1.79~2.03 μm·(104次)-1;内轨裂纹萌生寿命约为8.00×105次以上,对应通过总质量约为1.46×107t,平均磨耗发展率约为1.69 μm·(104次)-1.
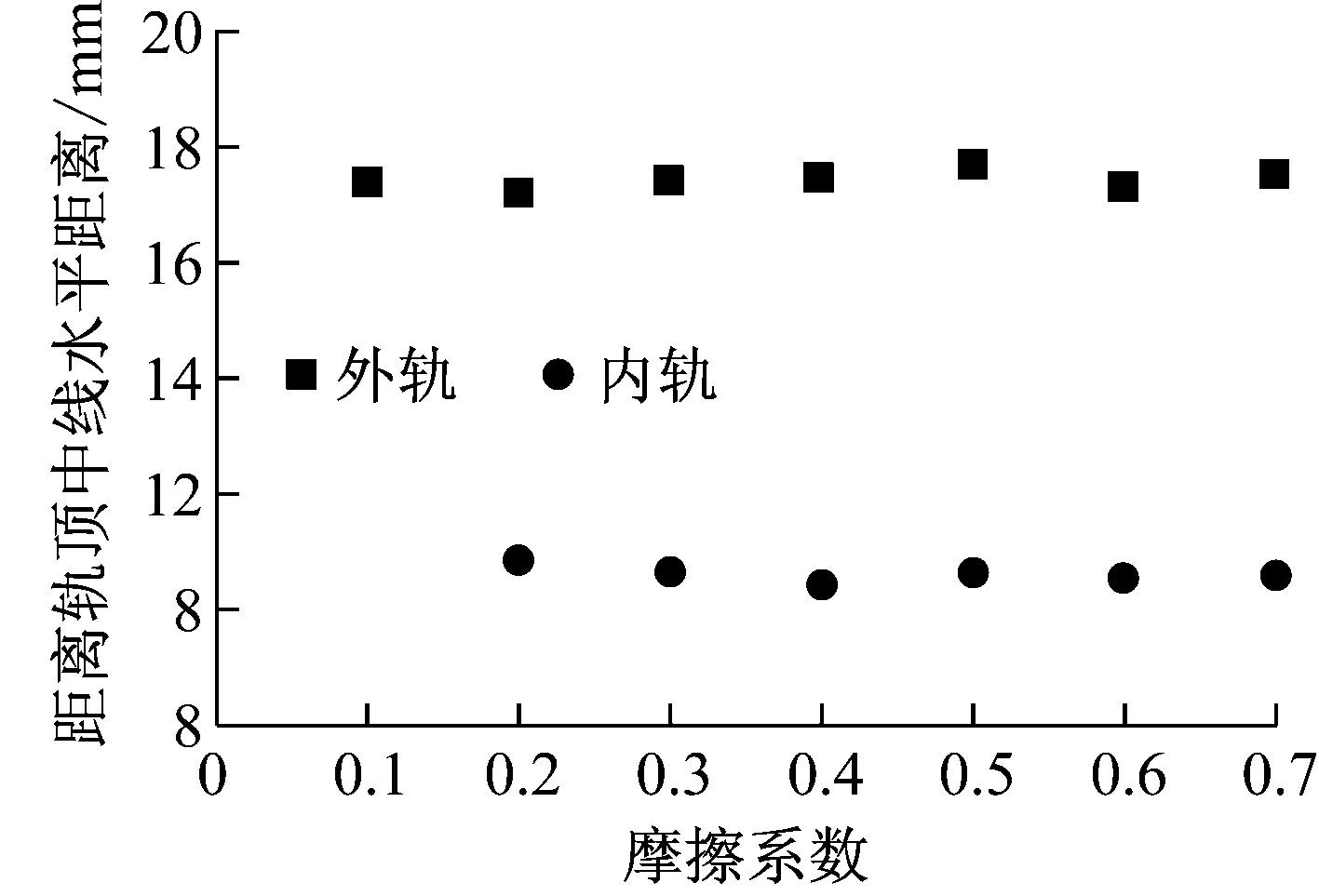
a 裂纹萌生点距离轨顶中线水平位置
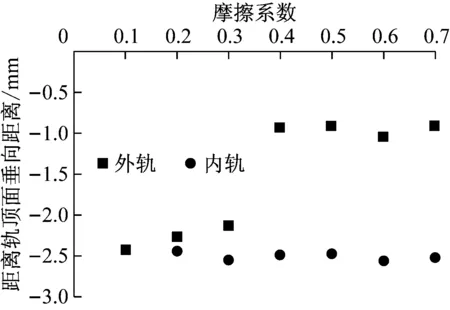
b 裂纹萌生点距离轨顶面垂向位置
Fig.12Crackinitiationpositioninrailswithdifferentfrictioncoefficient
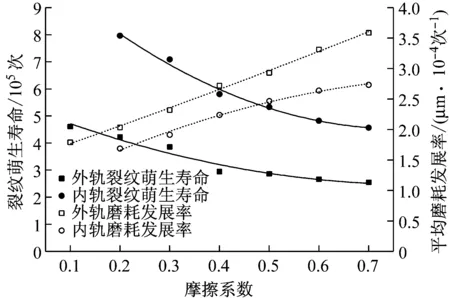
图13 不同摩擦系数下钢轨裂纹萌生寿命与平均
Fig.13Railcrackinitiationlifeandaverageweargrowthratewithdifferentfrictioncoefficient
(2)当摩擦系数在0.3~0.4之间时,外轨裂纹萌生寿命约为2.94×105~3.86×105次,对应通过总质量约为5.29×106~6.95×106t,平均磨耗发展率约为2.32~2.72 μm·(104次)-1;内轨裂纹萌生寿命约为5.81×105~7.09×105次,对应通过总质量约为1.05×106~1.28×107t,平均磨耗发展率约为1.92~2.24 μm·(104次)-1.
(3)当摩擦系数在0.5~0.7之间时,外轨裂纹萌生寿命约为2.55×105~2.86×105次,对应通过总质量约为4.10×106~4.67×106t,平均磨耗发展率约为2.94~3.59 μm·(104次)-1;内轨裂纹萌生寿命约为4.57×105~5.33×105次,对应通过总质量约为8.36×106~9.75×106t,平均磨耗发展率约为2.46~2.73 μm·(104次)-1.
以摩擦系数0.3~0.4时的裂纹萌生寿命和磨耗发展率作为基准,对比其他摩擦系数的相应结果发现,摩擦系数在0.1~0.2时,尽管外轨和内轨的裂纹萌生寿命分别延长了1.1~1.6倍、1.1~1.3倍,外轨和内轨的平均磨耗发展率分别降低了12%~34%、12%~25%,但摩擦系数较小有可能造成轮轨黏着降低、车轮打滑;摩擦系数在0.5~0.7时,外轨和内轨的裂纹萌生寿命分别降低了3%~34%、10%~35%,平均磨耗发展率分别增加了8%~55%和10%~43%,且摩擦系数越大,裂纹萌生寿命降低幅度和平均磨耗发展率增加幅度越大.
再对比摩擦系数0.3、0.4、0.5时的裂纹萌生寿命和平均磨耗发展率,摩擦系数从0.5降低到0.4,外轨和内轨的裂纹萌生寿命分别延长3%和10%,而相应的平均磨耗发展率降低分别为8%和10%;摩擦系数从0.4降低到0.3,外轨和内轨的裂纹萌生寿命分别延长31%和20%,而相应的平均磨耗发展率降低分别为15%和14%,因此,将轮轨摩擦系数控制在0.3~0.4间可以得到较长的裂纹萌生寿命和较小的平均磨耗发展率.
4 结论
(1)根据一定车轮通过次数即一定通过总重下的钢轨磨耗累积和型面变化,考虑轮轨接触、钢轨材料疲劳损伤、磨耗型面形成和替换、疲劳损伤累积等过程,建立了钢轨疲劳裂纹萌生与磨耗共存发展预测模型,可以同时分析裂纹萌生和磨耗发展情况.
(2)改变轮轨接触位置的摩擦系数对接触斑位置、形状和面积无影响,但会影响接触斑黏着区/滑动区的分布状态,从而影响钢轨疲劳裂纹萌生寿命与磨耗.随着摩擦系数的增大,黏着区面积增大,滑动区面积减小,接触斑横向、纵向切应力增大.摩擦系数从0.3增大至0.5、0.7时,接触斑横向、纵向切应力分别增大约20%、80%和30%、30%,但法向应力基本保持不变.
(3)随着摩擦系数的增大,钢轨的平均磨耗发展率增加、磨耗量增大.摩擦系数从0.3增大至0.7时,外轨的平均磨耗发展率增加约17%~55%;内轨的平均磨耗发展率增加约16%~42%.在同一摩擦系数下,在裂纹萌生前,每个磨耗型面替换过程的阶段磨耗发展率随着车轮通过次数的增加呈递减趋势,在裂纹萌生时,外轨和内轨的磨耗量分别约为0.14~0.18 mm、0.16~0.18 mm.
(4)随着摩擦系数的增大,内、外轨的裂纹萌生寿命均减小,摩擦系数从0.3增加至0.7,外轨裂纹萌生寿命降低了约24%~34%,内轨裂纹萌生寿命降低了18%~35%.
(5)摩擦系数对外轨和内轨疲劳裂纹萌生位置的影响不同.各个摩擦系数条件下,外轨和内轨的裂纹萌生位置分别距离轨顶中心为17~18 mm和10~11 mm;随着摩擦系数的增加,外轨的裂纹萌生位置从轨面以下2.0~2.5 mm处向亚表面0.9~1.0 mm移动;内轨的裂纹萌生位置基本处于轨顶面下2.4~2.6 mm.
(6)轮轨接触位置的摩擦系数控制在0.3~0.4的范围,可以既延长相应位置的疲劳裂纹萌生寿命,也减缓磨耗.
