Baarda数据探测法中的粗差误判分析

杨 玲， 喻杨康

(同济大学 测绘与地理信息学院， 上海 200092)

粗差探测与识别是测绘、导航及相关领域的研究热点.在融合卫星定位、视觉导航等技术的多传感器融合导航定位系统中，观测数据量呈指数倍增加，提高了定位精度及可靠性.与此同时，系统冗余度增加导致粗差出现的概率及复杂度也成倍增加，故系统需具备更强的粗差探测与识别能力[1-4].

目前，粗差探测与识别方法主要有两类：一类将粗差纳入函数模型，认为粗差导致该观测值期望平移，由此发展了数据探测法[1-2]；另一类将粗差纳入随机模型，认为粗差与正常观测值等期望，但方差膨胀(变大)，由此发展了抗差估计理论[3-4].基于第一类思想，文献[1]最早提出了针对单粗差的数据探测法，基于已知单位权方差，利用服从正态分布的标准化残差作为统计量(data snooping).在此基础上，文献[5]根据观测值的多余观测分量判断其对粗差的容忍度，提出了一种基于局部分析法的粗差探测法.文献[6]基于真误差与观测值间的解析关系，提出了拟准检定法(QUAD)；文献[7]借鉴拟稳平差思想，附加“拟准观测的真误差范数极小”条件，解决了关于真误差的秩亏方程组求确定解的问题；文献[8-9]提出了多维粗差同时定位定值法(LEGE)，可同时定位并求解多个粗差.有学者证明，当观测值独立时以上3种方法理论等价[10-11].基于第二类思想，发展了适用于最小二乘平差的选权迭代法[3-4].文献[12]比较了数据探测法和选权迭代法抵抗粗差的效果差异；文献[13]构造了适用于相关观测值的等价权函数；文献[14]利用中位数法估计参数初值，提高了选权迭代法的抗差性.以上相关研究也广泛应用于导航定位[15-17]和方差分量估计[18]等平差问题.

不同数据探测法或抗差估计均通过建立观测值函数的统计量来进行粗差探测与定位.由于真误差不完全可知，因此，粗差探测可能发生误警和漏检[19-20].文献[21-23]基于误警和漏检概率提出了单粗差及多粗差影响下的系统内部和外部可靠性指标，但并未考虑粗差误判(错误定位)的可能.当系统中观测值统计量强相关，或存在多个粗差时，粗差误判概率将显著升高，并对参数估计造成更显著的偏差影响.文献[19]分析了粗差误判对摄影测量光束法平差的精度影响；文献[24]仿真计算了2个备选假设下的单个粗差的误判概率；文献[25]初步推导了多个备选假设下发生误警、漏检和误判的概率的近似计算公式，但估计精度有待提高.

虽已有研究对粗差误判的可能和原因进行了分析，但仍难以准确估计其对系统内、外部可靠性参数的影响.因此，详细讨论数据探测法中系统发生误警、漏检和误判的原因，理论推导多维备选假设下误警、漏检和误判概率与统计量间相关性的函数关系.

1 数据探测法

1.1 单个备选假设

Baarda数据探测法基于间接平差模型[9]

Ax+e=y

(1)

式中：y为n×1阶观测值向量;A为n×t阶列满秩设计矩阵;x为t×1阶参数向量;e为n×1阶观测误差.Q为n×n阶表征观测值精度的方差-协方差阵(正定阵)，则式(1)的参数及其方差的最小二乘解为

(2)

观测值残差及其方差的最小二乘解为

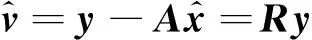
Qv=Q-AQxAT=RQ

(3)

式中：R=I-AQxATQ-1是幂等阵，表征了观测值与其残差间的映射关系，称为可靠性矩阵，与观测值无关，取决于设计矩阵A和协方差阵Q[1].

设平差系统中只存在单个粗差，数据探测法将粗差归入函数模型，认为粗差与正常观测值方差相同而期望不同，进而利用统计假设检验探测并剔除粗差.设观测值yi中含有粗差Δi，按式(1)～(3)平差后得粗差的估值Δi及其方差qΔ，进而可构造统计量wi[1].

(4)

当不存在粗差时，原假设成立，即H0:wi～N(0,1).若存在粗差，则备选假设成立，即H1:wi～N(δ0,1).

对于wi，选定显著水平α0和检验功效1-β0，或选定显著水平α0和非中心化参数δ0进行假设检验.若|wi|≤k0，则认为粗差不存在；若|wi|>k0，则认为存在明显粗差.其中，k0=μ1-α0/2为显著水平对应的标准正态分布的分位值.

一般而言，假设检验认为小概率事件在一次试验中不可能发生.然而事实上，小概率事件发生概率虽小，但仍存在.因而，一次试验中假设检验的结果可能与客观现实矛盾，产生弃真和纳伪错误，致使系统发生误警或漏检，如表1所示[1].

表1 单个备选假设时的检验抉择

表1中显示的是单个备选假设时假设检验的4种检验抉择，括号内为对应的概率值.换言之，在一个显著水平为α0的假设检验中，若原假设H0为真，错误选择备选假设的概率为α0，即P(|wi|>k0)=α0；反之，若备选假设H1为真，错误选择原假设的概率为β0，即P(|wi|≤k0)=β0.由此可推算非中心化参数δ0为

δ0=μ1-α0/2-μβ0

(5)

由式(4)、(5)可得最小可探测粗差MDB为[21]

(6)

1.2 多个备选假设

表2 多个备选假设时的检验抉择

表2为多个备选假设时的检验抉择.

(1) 当客观现实不存在粗差时，1-α00表示检验时若考虑多个备选假设则原假设H0被正确接受的概率为

1-α00=P(∩(|wi|≤k0)|H0)

∀i∈{1,2,…,n}

(7)

式中：P(*)表示事件“*”的概率；∩(*)表示多个事件“*”的并集；“|H0”表示在事件H0发生的条件下；“∀i∈{1,2,…,n}”表示变量i取1至n中的任意值，n为统计量wi的个数.α0i表示错误地放弃原假设而接受备选假设Hi的概率(称为弃真错误)为

α0i=P(|wi|>k0&&|wi|>|wk||H0)

∀k∈{1,2,…,n}&&k≠i

(8)

则，总的弃真概率为

α00=∑α0i

(9)

(2) 当客观现实是第i个观测值中存在粗差时,备选假设Hi被正确接受的概率为

1-βii=P(|wi|>k0&&|wi|>|wk||Hi)

∀k∈{1,2,…,n}

(10)

相应的纳伪概率为

βi0=P(∩(|wk|≤k0)|Hi)

∀k∈{1,2,…,n}

(11)

同时，存在误判概率为

γij=P(|wj|>k0&&|wj|>|wk||Hi)

∀k∈{1,2,…,n}

(12)

式(12)表示第j个观测值被错误判断为粗差的概率，则总的误判概率为

γi=∑γij

∀j∈{1,2,…,n}&&j≠i

(13)

式(7)～(11)表明，若阈值k0和非中心化参数δ0仍由单个备选假设检验的显著水平α0和检验功效1-β0决定，则此时真实的误警和漏检概率分别为α00和βi0，而非α0和β0.

2 多个备选假设下的3类误差分析

文献[25]研究表明，多个备选假设下的误警、漏检和误判概率受检验量间相关系数的影响，以以下2个备选假设为例进行分析.试验步骤如下：

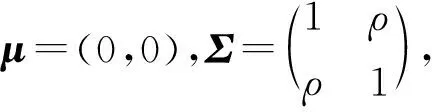
(2) 设显著水平(误警概率)α0=0.1%，统计ρ=0时的实际误警概率α00、α01、α02.

(3) 重复步骤(1)和(2)，取步长0.01，使ρ从0逐渐增加至1；则步骤(2)统计的3个参数α00、α01、α02可表示为相关系数ρ的函数，如图1所示.

(4) 设显著水平(误警概率)α0=0.1%、漏检概率β0=20%，则对应的非中心化参数δ0=4.13.

(6) 统计实际漏检概率β10及误判概率γ12.

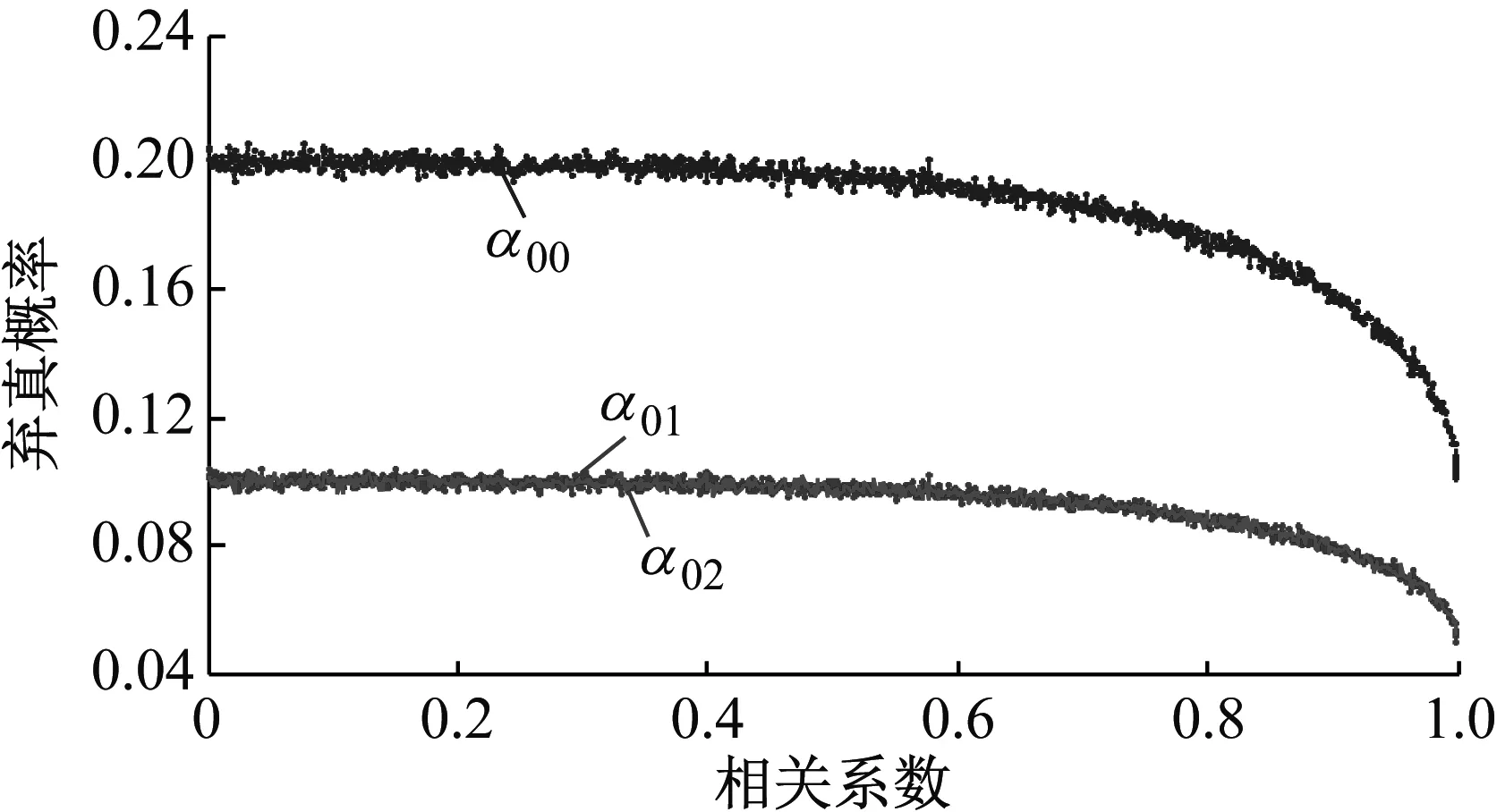
图1 误警概率随相关系数变化曲线

图2 漏检概率随相关系数变化曲线

图1显示，对正常系统(无粗差)进行2个备选假设的统计检验时，误警概率随相关系数ρ的增大逐渐降低，且这几个误警概率之间满足：α00=α01+α02，由对称性原理可得α01=α02，因而α00=2α01.当设α0=0.10%时，相关系数ρ=0对应的误警概率为α00=0.20%=2α0，α01=α02=0.10%=α0；相关系数ρ=1.0对应的误警概率分别为α00=0.10%=α0，α01=α02=0.05%=α0/2.

图2和图3为实际第1个观测值中存在粗差时系统的漏检和误判概率随相关系数的变化曲线.图2显示当两统计量间相关系数为零时，系统真实的纳伪概率β10与β0(20%)相等.而随着相关系数ρ的增加，β10先递减，随后又迅速递增至一个略低于β0的值.图3显示，误判概率随相关系数ρ单调递增，当ρ从0.8增加至1.0时，误判概率从6%增加至40%.可见相关系数越大，数据探测法的误判概率就越高，进而严重影响探测成功率及参数估计的可靠性.当ρ=0和ρ=1时，3类错误概率可直接由式(7)～(11)计算，列于表3.该表显示，其结果与图1至图3的极值情况相符.

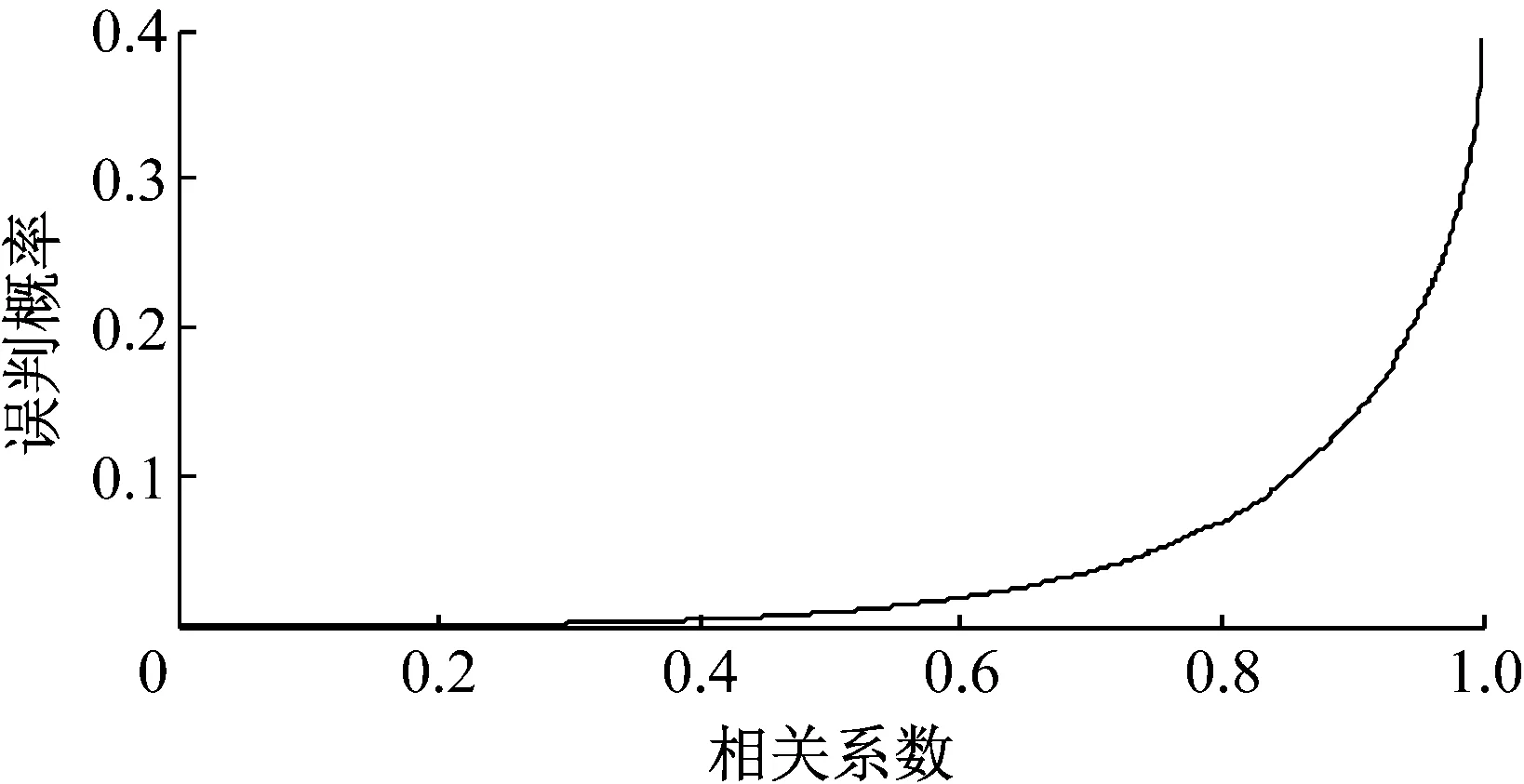
图3 误判概率随相关系数变化曲线

以上分析基于2个备选假设，实际应用于多个备选假设的统计假设检验时，n个观测值对应n个统计量wi，两两统计量的相关系数为ρij，则共有n(n-1)/2个相关系数，且这些相关系数各不相同.因而，误警、漏检和误判的概率计算更为复杂，无法理论推导得解析解，只能通过大量蒙特卡洛仿真模拟进行统计.

表3 ρ=0与ρ=1时2个备选假设下的误警、漏检和误判概率

3 试验分析

为分析统计量间相关性对系统粗差探测能力的影响，以图4水准网为例进行分析，其对应的观测值及其已知信息列于表4(例1).

图4 水准网的示意图

表4给出了观测值l1至l6及待定参数D、E、F三点高程的真值，为排除一次观测中偶然误差的影响，通过构建大量服从已知正态分布的观测误差(期望为零，方差阵Q为权阵P的逆阵)及粗差来统计误警、漏检和误判的概率.

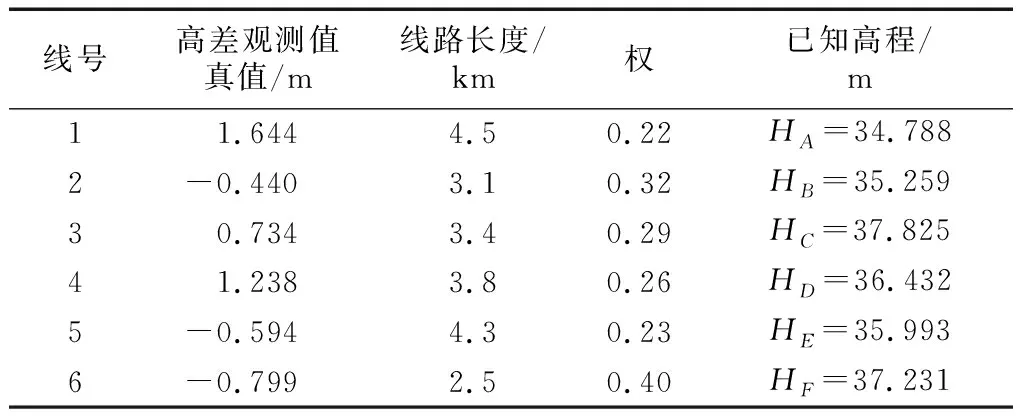
表4 水准网路线观测值

3.1 w检验

首先，为了研究偶然误差对观测值残差的影响，对观测值L=(l1,l2,l3,l4,l5,l6)T加入服从正态分布N(0,Q)的偶然误差，模拟次数为2×106，进行最小二乘平差及w检验.统计假设检验量wi由式(4)求得，检验量之间的相关系数由式(14)求得，并列于表5.

(14)

表6显示了当观测值仅含偶然误差时，统计量|wi|>k0的概率(α0=0.1%).可见，对任意仅含偶然误差的观测值进行单个备选假设的w检验时，其

表5 统计量w的相关系数矩阵

表6 无粗差时|wi|>k0的概率

误警概率即为置信水平α0.

空气热源热泵（即风冷热泵）具有冬季供热、夏季制冷的双重功能，使用它具有以下优势：可以省却锅炉和锅炉房；供热无污染，能量利用系数高；机组可在室外安置，不需专用机房；减少土建工程的投资；不采用冷却塔，免除冷却水系统的投资；运行过程采用自动化控制；机组安装方便；管理和维修简单。目前已在我国长江以南地区得到广泛应用。由于新疆地区冬季严寒期较长且降雪量大，热泵能效比会下降到很低甚至不能正常工作，因此，在新疆地区仍停留在探索阶段，不能普遍使用。

表7显示了分别在各观测值中加入1倍中误差大小的粗差时统计量|wi|>k0的概率.可见，各观测值统计量对粗差的敏感程度不同，且粗差不仅使其对应的统计量变大，也不同程度地影响了其他观测值统计量，从而导致粗差可能错误定位.例如，在l4上加入粗差，将导致|w6|>k0的概率为0.22%.

Tab.7Possibilityof|wi|>k0withanoutlier%

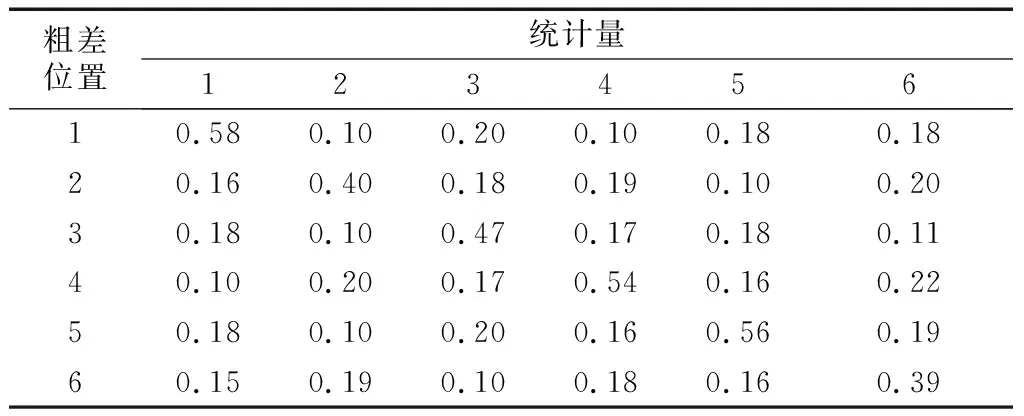
表8显示了当在各观测值中加入3倍中误差大小的粗差时，统计量|wi|>k0的概率.与表7对比可知，粗差越大，其被成功探测的概率也越高.但各观测值对粗差的敏感程度存在差异，这是由式(3)中R阵对角元素Rii决定的.此外，第i个观测值上的粗差除了影响其自身统计量，也影响其他观测值统计量.当某一观测值li存在粗差时，其他统计量|wj|>k0的概率亦随之增加，且增幅与其之间的相关系数正相关.

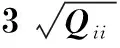
Tab.8Possibilityof|wi|>k0withanoutlier%

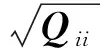
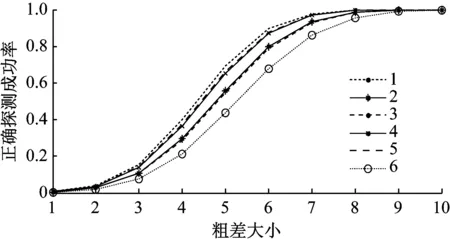
图5 各观测值上加入粗差时成功检测的概率

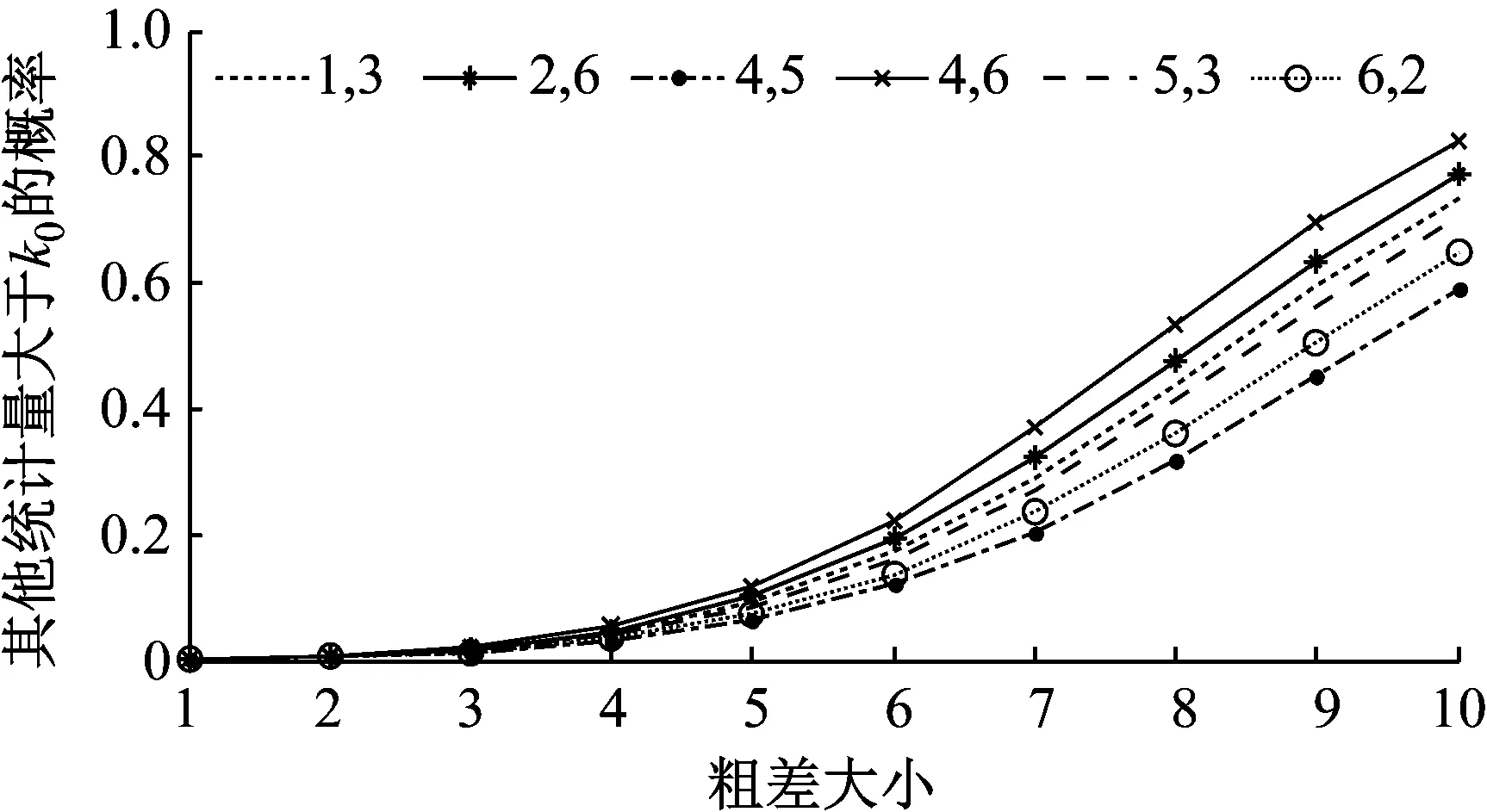
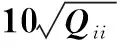
Fig.6Possibility of |wj|>k0with the outlier onli

3.2 MDB的计算与检验

Baarda数据探测法中定义了最小可探测粗差(MDB，minimal detectable bias)，其数学含义是当粗差大小为MDB时，以分位值k0=μ1-α0/2作为阈值，则|wi|≤k0的概率即为漏检概率β0.

取α0=0.1%、β0=20%，表9为水准网中各观测值的MDB值.依次在各观测值上加入其MDB大小的粗差，统计各观测值统计量超限的概率，列于表10.该表中，对角元素为各观测值上粗差被成功探测的概率，均接近其理论值80%；非对角元素表示某观测值上的粗差被错误定位到其他观测值的概率.对比表5可知，统计量间的相关系数越大，对应位置上的误判概率就越大.

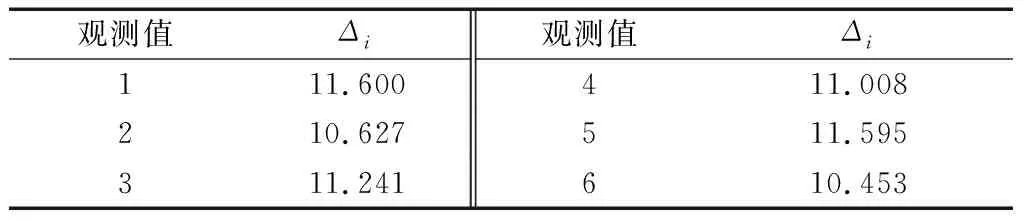
表9 各观测值的MDB

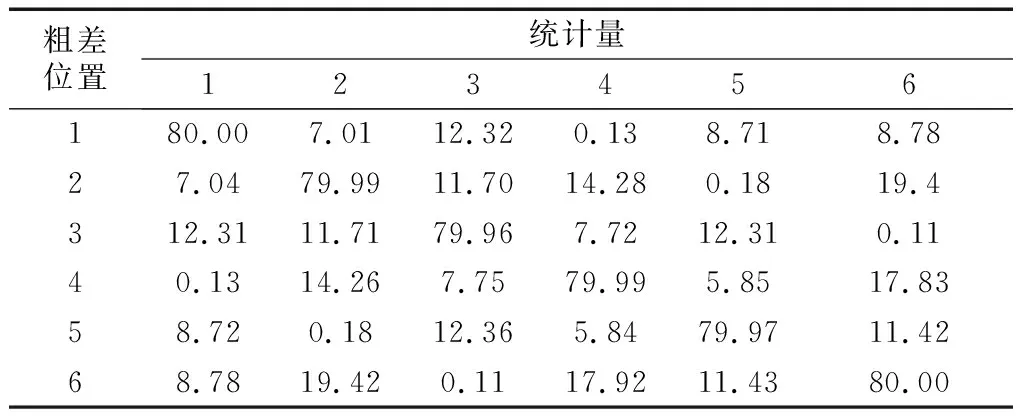
表10 粗差大小为MDB时|wi|≤k0的概率

3.3 数据探测法中的粗差误判分析

在实际应用中，即便只存在单个粗差，由于统计量之间的相关性，该粗差可能导致多个检验量均大于阈值k0.然而，数据探测法的实际过程是每次仅剔除最大统计量对应的观测值而利用剩余的观测值重新平差，直到所有的统计检验量均小于k0.因此，数据探测法的实际检验条件为仅当

|wi|>k0&&|wi|>|wk||Hi

∀k∈{1,2,…,n}&&k≠i

(15)

时认为第i个观测值存在粗差.针对这一条件进行统计分析，对于图4所示水准网，将大小为其MDB值的粗差依次加入各观测值中，将式(15)成立的概率列于表11.

表11例1中粗差大小为MDB时数据探测法的成功率、误判率及漏检率

Tab.11 Possibility of successful identification, wrong exclusion and missed detection while outlier size is MDB (example 1) %

注：黑体为成功率.

表11中，对角线数值表示粗差正确定位的概率，非对角线数值表示粗差被误判到其他观测值上的概率，最后一列数值表示漏检概率.如第1行数据显示，l1上的粗差被误判到l3的概率是1.02%，而被误判到l4上的概率仅为0.01%.这一误判错误是由检验量间的相关性导致的，这也是数据探测法的主要问题及重点讨论内容.对比表5可知，误判概率与两统计量之间的相关系数呈正相关.

3.4 另一网型下的第3类错误分析

为对比不同网形中相关系数对误判概率的影响，采用一组单历元GPS伪距观测数据进行实验分析.对原始观测方程进行线性化后得到最小二乘的函数模型和随机模型如下(例2).

原始观测值矩阵L=(2.070 0.800 -2.5811.818 -0.880 0.174 2.081 0.171)T.

系数矩阵A=

观测值权阵Q=diag(145.055 85.807 67.511 31.461 176.927 9.590 199.721 10.372).

得其观测值对应统计量之间的相关系数矩阵为

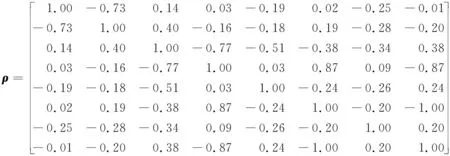
统计分析结果列于表12，其加入的粗差大小是取α0=0.1%、β0=20%时各观测值的MDB值.对角线数值为依次在各观测值中加入其MDB大小的粗差时该粗差被正确探测的概率，非对角线数值为误判概率，最后一列为漏检概率.对比各行数值可知，当l7含粗差时漏检概率最高，为19.36%；而l4含粗差时，漏检概率最低，为17.44%.然而，在实际应用中，由于误判错误的影响，漏检概率并不能完全反映数据探测法的成功率.检验量间相关系数越大，误判概率就越高，相应的粗差探测成功率就越低.例如该例中，相关系数|ρ68|高达1，所以当l6含粗差时，其被正确探测的概率只有34.68%，而被误判到l8上的概率却高达35.35%.因此，当观测值检验量间的相关系数很大时，误判错误可能是影响粗差探测正确率的重要因素.

对比表11和表12可知，在不同网形中，MDB的有效性差异很大.例1网形中各统计量间的相关系数分布较均匀，最大值为0.587 3.对应的误判概率最大不超过2%，因而并未对系统粗差探测成功率造成显著影响，此时MDB仍可有效表征系统的内部可靠性.在例2网形中，某些统计量间的相关性很强，如|ρ68|达到1.00，其他如|ρ46|、|ρ48|也都高达0.87.相应的，表12中各观测值上的粗差探测成功率都显著降低.

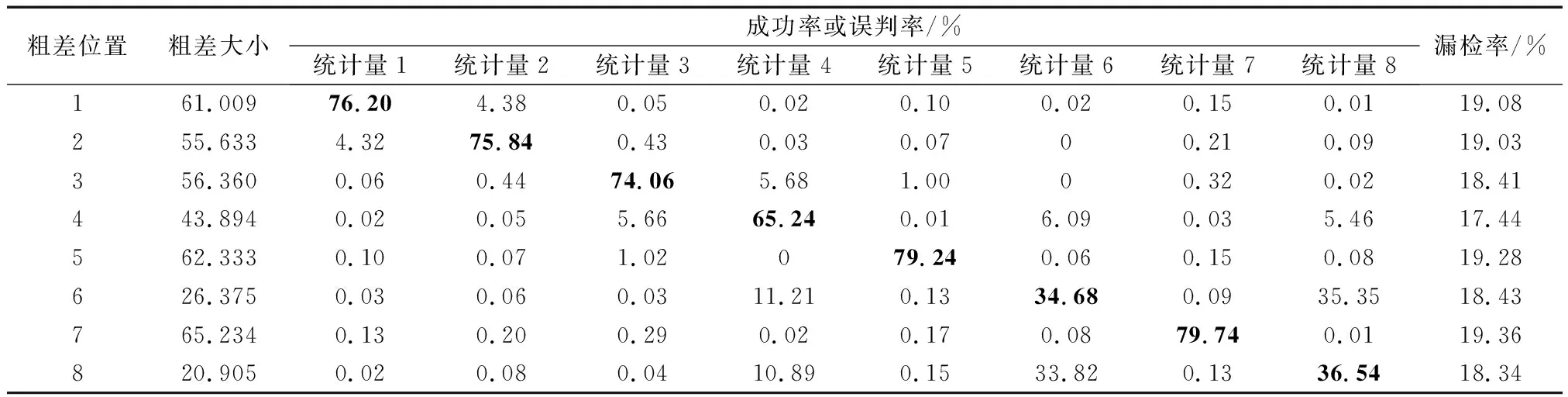
表12 例2中粗差大小为MDB时数据探测法的成功率、误判率及漏检率

注：黑体为成功率.

4 结论

理论和算例分析表明，数据探测法的误警、漏检和误判概率与统计量间相关系数相关，尤其当统计量间强相关性时，误判概率显著增加.传统的数据探测法仅考虑了误警和漏检，而忽略了系统误判的可能，从而导致真实的粗差探测成功率低于其理论值.为削弱这一影响，应尽量使平差系统中各观测值检验量间的相关系数较小.式(14)显示相关系数由可靠性矩阵R和观测值方差阵Q决定，而可靠性矩阵R取决于设计矩阵A和权阵P，因此需设计科学合理的网形，才能使得系统粗差探测的效果更优.而对于很多测量问题，初始网形一经采用，无法更改，此时，必须考虑该网形中观测值统计量间的相关系数，计算真实的误警、漏检和误判概率作为粗差探测及系统可靠性评估的指标之一.