帽型钢板桩挡墙土压力分布离心模型试验

刘 芳， 刘春影， 郑 实， 蒋明镜

(1.同济大学 土木工程防灾国家重点实验室，上海 200092；2.同济大学 岩土及地下工程教育部重点实验室，上海 200092)

钢板桩挡墙具有可重复利用、减少开挖量和节约材料等优点.随着低碳环保理念的提升，近年来钢板桩被广泛用于临时或永久基坑、堤坝和码头等工程的挡土挡水结构中.在进行钢板桩挡墙设计时，土压力计算一般沿用传统的平面挡墙分析方法，不考虑钢板桩挡墙与土体接触界面起伏所引起的土压力变化(即形状效应).

文献[1]最早述及基坑现场监测到的钢板桩挡墙土压力的形状效应，指出在基坑开挖过程中钢板桩挡墙凹凸处的土压力将逐渐产生差异，建议在类似支护工程土压力监测中考虑测点布置的影响.Tan等[2]和Nakayama等[3]分别在现场监测和现场足尺试验中证实了钢板桩挡墙横向土压力的不均匀分布，但未对产生机理进行定量分析.为了定量研究由于钢板桩截面形状所造成的土压力差异，笔者[4-5]采用有限元方法分析了不同指定位移模式下的钢板桩挡墙土压力分布规律，试图解释钢板桩挡墙土压力形状效应的物理机制和影响因素；Tong等[6]采用离心模型试验，模拟了非平面刚性挡墙的土压力变化规律.但上述定量研究或简化挡墙位移边界[4-5]，或将挡墙近似为刚性结构[6]，未能全面考虑钢板桩作为柔性挡墙的位移模式特点，钢板桩挡墙土压力形状效应的定量研究还有待深入.

鉴于此，采用离心模型试验，对缩尺帽型钢板桩(亦称U型钢板桩)挡墙支护基坑开挖过程进行了模型试验，考虑开挖条件下帽型钢板桩挡墙的变形过程以及所引起的土压力空间分布规律.

1 试验介绍

1.1 试验设备

采用同济大学TLJ-150土工离心机，该设备最大承载能力是150g·t，最大离心加速度为200g，最大荷重为2 t，有效旋转半径为3 m.所选择的模型箱长600.0 mm、宽400.0 mm、高500.0 mm.

1.2 模型设计

进行2组平行试验：帽型钢板桩挡墙试验(T-H)和平板挡墙试验(T-P)，图1为T-H试验的模型示意图，离心模型比为36.T-P试验将钢板桩挡墙置换成截面刚度相同的平面挡墙，其余试验条件不变.

如图1a所示，模型箱一侧预留宽50.0 mm的排水槽以便加快固结时间.挡墙宽度为350.0 mm，包含14节帽型钢板桩，帽型桩原型为日本新日制铁公司的帽型钢板桩(产品型号HS-SP-10H)，钢板桩的模型尺寸见图1a内的详图，截面宽度为25.0 mm.钢板桩搭接锁扣的加工尚难达到精度要求，为避免锁扣加工误差所带来的不确定因素，在模型中未考虑锁扣，模型挡墙采用厚0.3 mm的铁板，通过预制模具轧制而成，墙体材料的弹性模量约为210 GPa，泊松比为0.3.由于忽略了锁扣，墙体整体抗弯刚度将有所增加，同样开挖条件下墙体位移会有所减小，但土压力的形状效应不会有本质改变.平行试验的平板挡墙采用相同材料，墙厚为3.0 mm，原型截面刚度与帽型钢板桩相等(即9.43×107mm4).

如图1b所示，模型地基的厚度为460.0 mm，分为2层.上层为厚210.0 mm的黏土层，采用上海地区典型4号土.表1给出了该黏土的物理和力学指标，其中，剪切强度指标通过固结不排水三轴压缩试验测得，所测试样为离心模型试验后所切取的土样.模型地基下层为厚250.0 mm的砂层，采用上海长兴岛的吹填砂，平均粒径为0.13 mm，级配曲线的不均匀系数为1.5.基坑开挖深度为150.0 mm，分4层开挖，开挖深度依次为40.0 mm、50.0 mm、40.0 mm和20.0 mm.挡墙总高度为400.0 mm，出露土层表面40.0 mm，用以布设激光位移传感器测点，开挖全部完成后的挡墙嵌入深度为210.0 mm，与墙体总有效墙高(即开挖前墙体的初始入土深度H=360.0 mm)的比值为0.58，与文献[3]的现场试验条件一致.

b 立面

表1 试验黏土的物理力学指标

1.3 测量元件布设方案

试验过程中测量了墙顶位移、墙体应变、土压力以及土中孔隙水压力等，受试验条件所限，未能监测土体位移.墙顶位移通过激光位移传感器进行量测.在挡土侧土体中埋深85.0 mm和243.0 mm处各布设了1组微型孔隙水压力计(见图1b)，以监测固结过程中孔隙水压力消散情况.如图2所示，墙后(填土侧)距填土表面埋深85.0 mm、160.0 mm、243.0 mm处布设了微型土压力计，埋深85.0 mm和243.0 mm处布设了应变片；墙前(开挖侧)土压力计布设在埋深243.0 mm处，应变片分别布设在埋深85.0 mm和243.0 mm处.为减小传感器的尺寸影响，选择了尺寸尽可能小的测量元件，孔压传感器外径8.0 mm、厚3.0 mm，土压力计外径8.0 mm、厚2.0 mm，应变片尺寸为1.0 mm×1.0 mm.

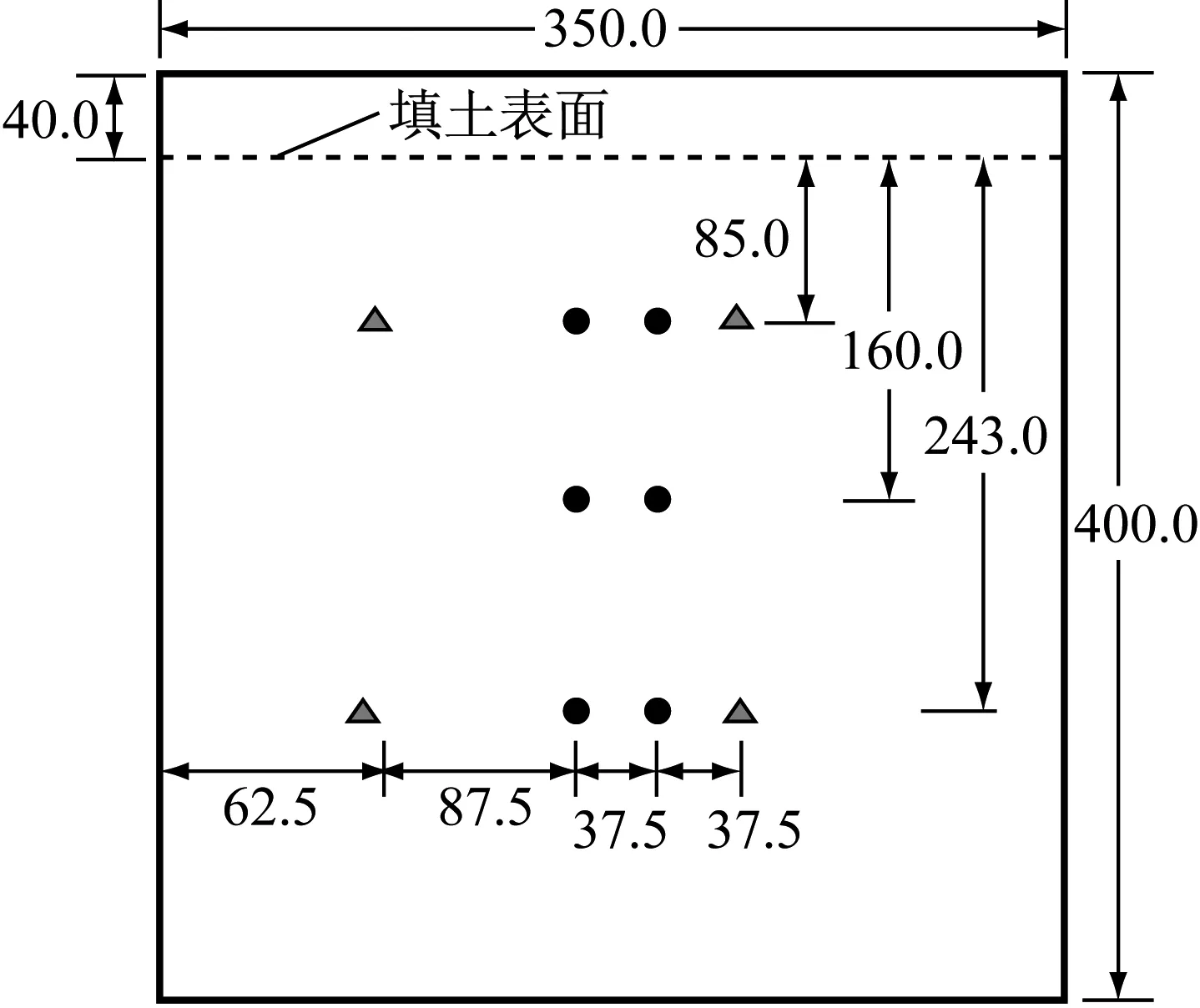
a 填土侧

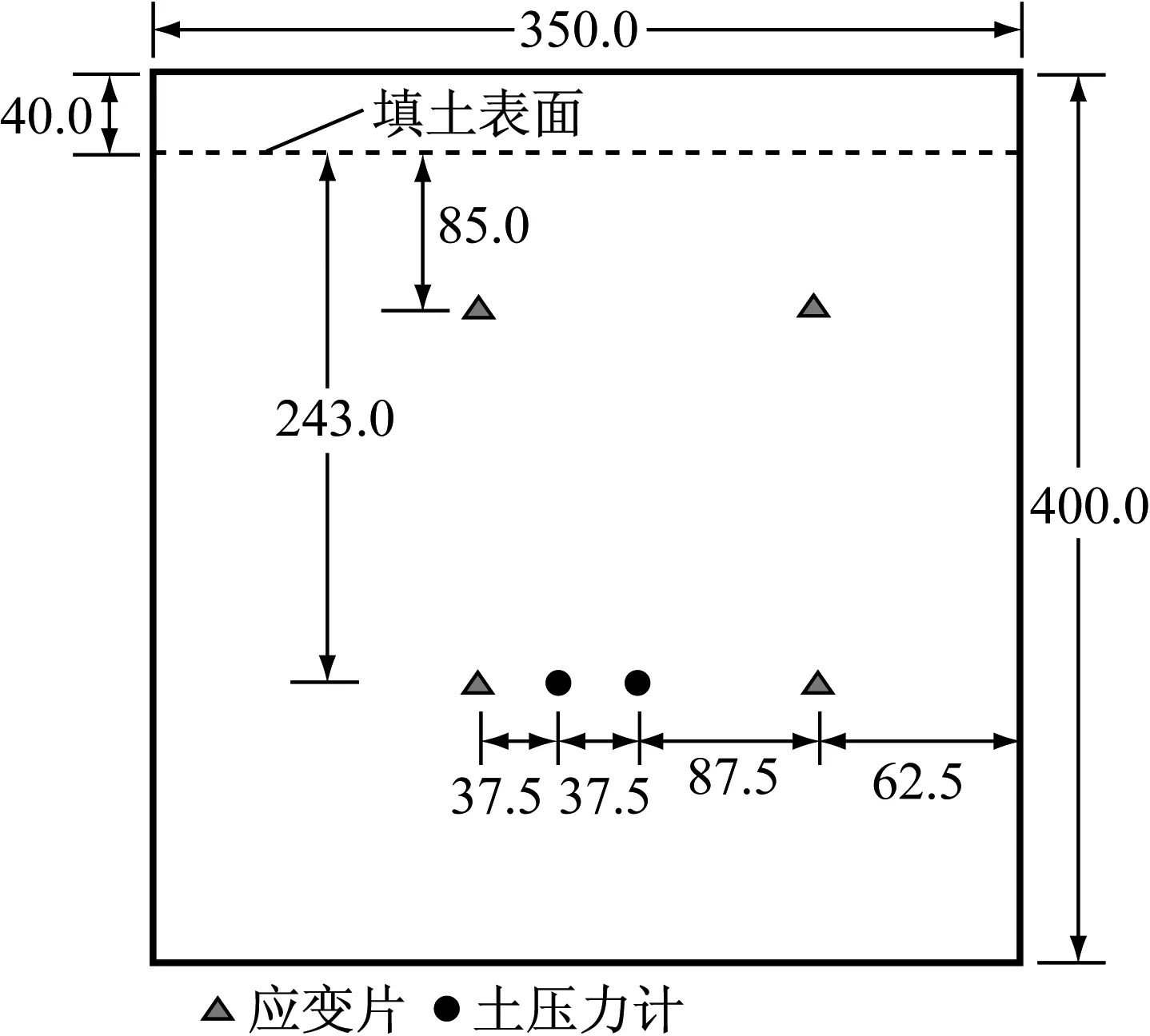
b 开挖侧

Fig.2Illustrationoftheinstrumentationonthesheetpilewall(unit:mm)

1.4 试验步骤

试验步骤分4个阶段：模型准备/制备、地基固结、模拟开挖和拆样.

(1) 模型准备/制备.标定土压力计和孔压计，并布设在模型墙预设位置.模型箱侧壁涂抹硅油以减少摩擦.烘干、粉碎黏土，用0.5 mm筛子过筛后放入真空搅拌机，加水搅拌并进行真空饱和.将干砂分为5层填筑，每层厚度50.0 mm，击实至目标孔隙比0.8(相对密实度约47%，密度约1.94 g·cm-3).随后将饱和后的黏土分层填在砂层之上直至与模型箱表面相平.将帽型钢板桩挡墙插入土中至指定深度.为了保持土体处于饱和状态，在排水槽内注水直至与土层表面齐平.将模型箱吊入离心机准备固结试验.

(2) 地基固结.上海地区4号土一般略微超固结[7]，平均固结比约1.08，因此固结时离心加速度设置为40g，稍大于开挖阶段的离心加速度.当孔隙水压力在1 h内的孔压变化为总变化量的3%时，认为固结基本完成.图3为钢板桩挡墙试验中不同深度处孔隙水压力消散情况，固结试验分3天完成(因安全原因晚上停机)，累计固结时间大致在18～20 h.固结结束后，停机，安装T-bar微型贯入仪.重启离心机，在36g离心加速度下运行直至孔压基本稳定，进行贯入试验，检测试样制备情况.不同模型试验的贯入数据大体一致，在黏土和砂土界面处有清晰分界.

图3 固结过程的孔压消散(TH试验)

(3) 模拟开挖.停机进行基坑第1层开挖.随后离心机重启至36g加速度，保持运行状态直至孔压和土压力测值基本保持稳定.停机进行下一层开挖，重复试验直至基坑开挖全部完成.

(4) 拆样.停机，分别测量墙体两侧5个不同深度处的土壤孔隙比e和含水量ω，表2为各深度处的平均测值.黏土层孔隙比在1.03至1.18之间，随深度略有降低，饱和度超过97%，2组试验在相同深度处的测量结果比较接近，平板墙试验的黏土层孔隙比高于钢板桩试验，推测前者的固结度稍低于后者.砂层的饱和度较低，因为砂层渗透系数高，拆样后水分流失较快.

表2试验后模型土样物性测定结果

Tab.2Voidratioandwatercontentofthesoilsafterthecentrifugetests

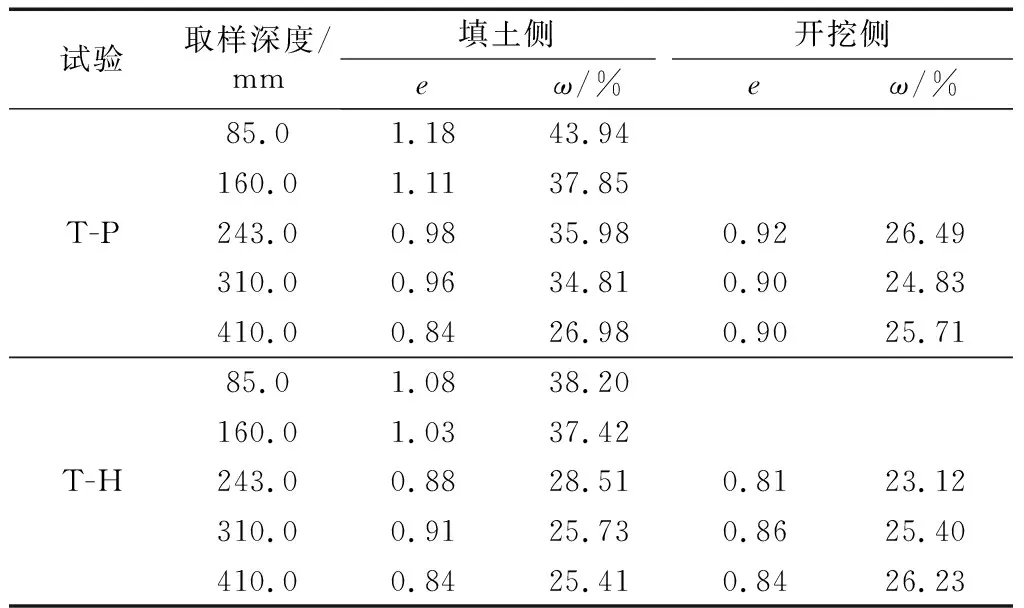
试验取样深度/mm填土侧开挖侧eω/%eω/%85.01.1843.94160.01.1137.85T-P243.00.9835.980.9226.49310.00.9634.810.9024.83410.00.8426.980.9025.7185.01.0838.20160.01.0337.42T-H243.00.8828.510.8123.12310.00.9125.730.8625.40410.00.8425.410.8426.23

2 试验结果

2.1 墙体变形

2组试验的墙顶水平位移测量结果如图4所示，各开挖深度所对应的水平位移值为离心机运行过程中位移测值稳定段的平均值，由于第3次开挖之后，位移计已超过量程，因此没有获得测值，图4仅给出了前2次开挖的测量结果.位移值δ和开挖深度x均采用有效墙高H进行量纲一化.如图所示，墙顶位移随开挖深度增加而增加；在相同开挖深度下，平板墙的位移大于钢板桩，这与2组试验的地基性质差异有关，拆样后平板墙地基的孔隙比量测结果大于钢板桩地基相应结果，因此前者墙体位移也较大.

图4 墙顶水平位移随x/H的变化曲线

Fig.4Horizontaldisplacementatthetopofthewallsatdifferentnormalizedexcavationdepthsx/H

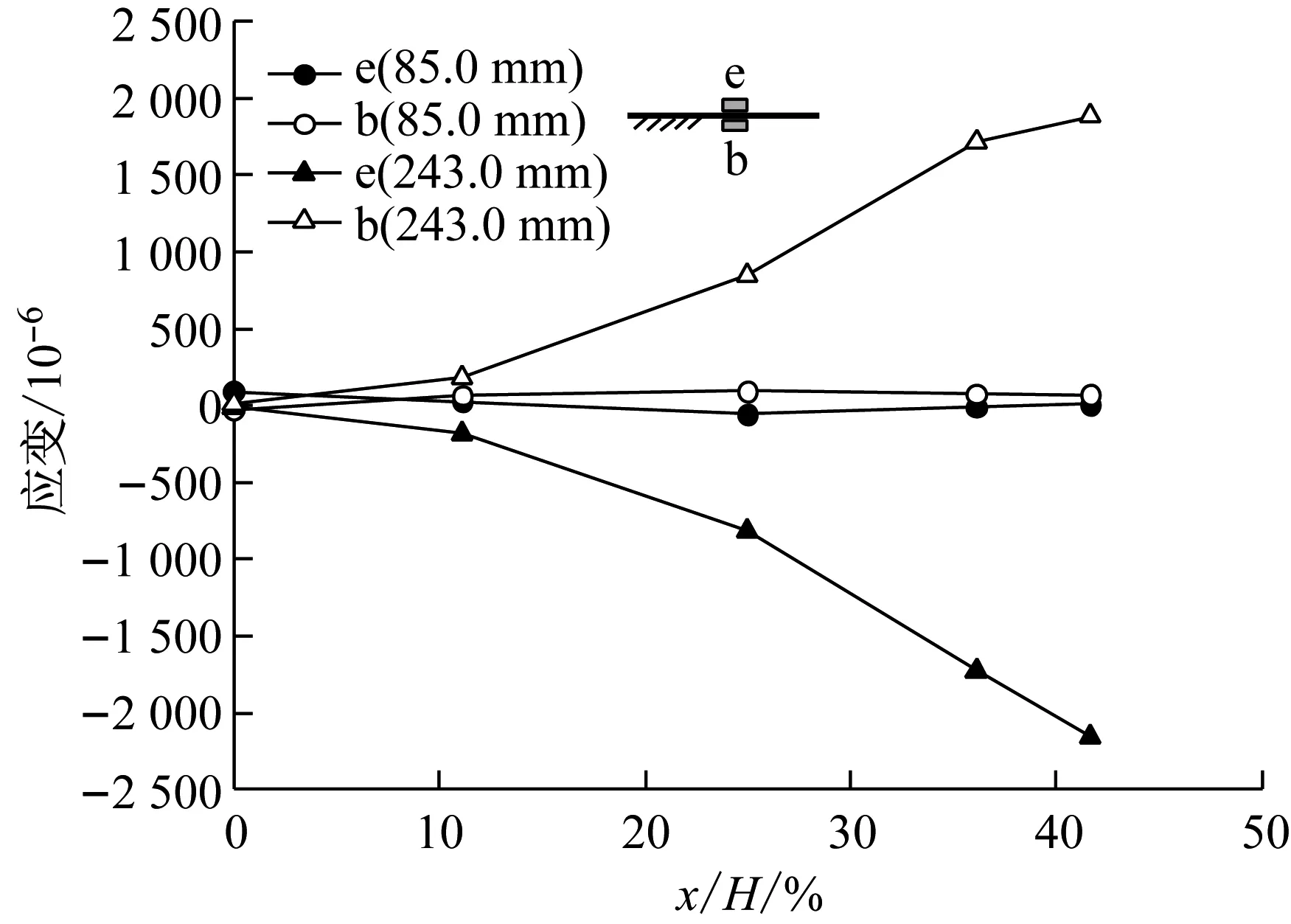
图5为2组试验测得的墙体两侧的竖向应变与开挖深度的关系曲线，其中拉为正、压为负.测点编码中的A、B分别代表同一高层不同位置，e代表开挖侧，b为填土侧.结果表明，平板桩和钢板桩填土侧的墙体受拉，开挖侧受压，说明桩身整体向开挖侧弯曲，应变绝对值均随埋深增加而增加.

2.2 土压力竖向分布

图6a和6b分别为不同埋深(d)填土侧钢板桩挡墙迎土面凹处(Ab)和凸处(Bb)土压力在开挖过程的变化.由于Bb位置埋深85.0 mm处的土压力传感器在试验过程中出故障，未能得到测试数据.如图所示，开挖前，土压力分布接近静止土压力理论曲线；随着开挖深度增加，除凸处埋深160.0 mm的土压力在第4层开挖时土压力略有增加，其余测点土压力逐渐减小并趋近朗肯主动土压力分布曲线；土压力在前2层开挖时变化较大，后2层开挖时变化较小.当开挖完成时，砂土层土压力小于朗肯主动土压力理论值，由于朗肯理论忽略墙土摩擦，主动土压力估计值可能偏大.平板挡墙土压力沿深度分布规律与钢板桩挡墙类似，不再赘述.

a 平板墙

b 钢板桩挡墙

2.3 钢板桩挡墙横向土压力分布特征

2.3.1开挖侧

图7为开挖侧埋深243.0 mm处钢板桩挡墙不同部位的土压力在开挖过程的变化情况.当开挖深度小于30%H时，开挖侧迎土面凸处(即Ae测点)土压力大于凹处(即Be测点)；当开挖深度继续增加时，Ae处土压力急剧下降，开挖完成时该处土压力值小于Be处相应测值.

2.3.2填土侧

图8为填土侧不同埋深处钢板桩挡墙不同部位土压力在开挖过程的变化情况.在埋深160.0 mm处，当开挖深度较小时，Ab处土压力大于Bb处相应值，随着开挖深度增加，二者大小关系产生反转.埋深243.0 mm处Ab和Bb测点的土压力变化规律与埋深160.0 mm处规律类似，开挖较浅时Ab处土压力大于Bb，随着开挖深度增加，Ab处土压力减小幅度大于Bb，二者大小关系呈现反转趋势.

a 迎土面凹处测点

b 迎土面凸处测点

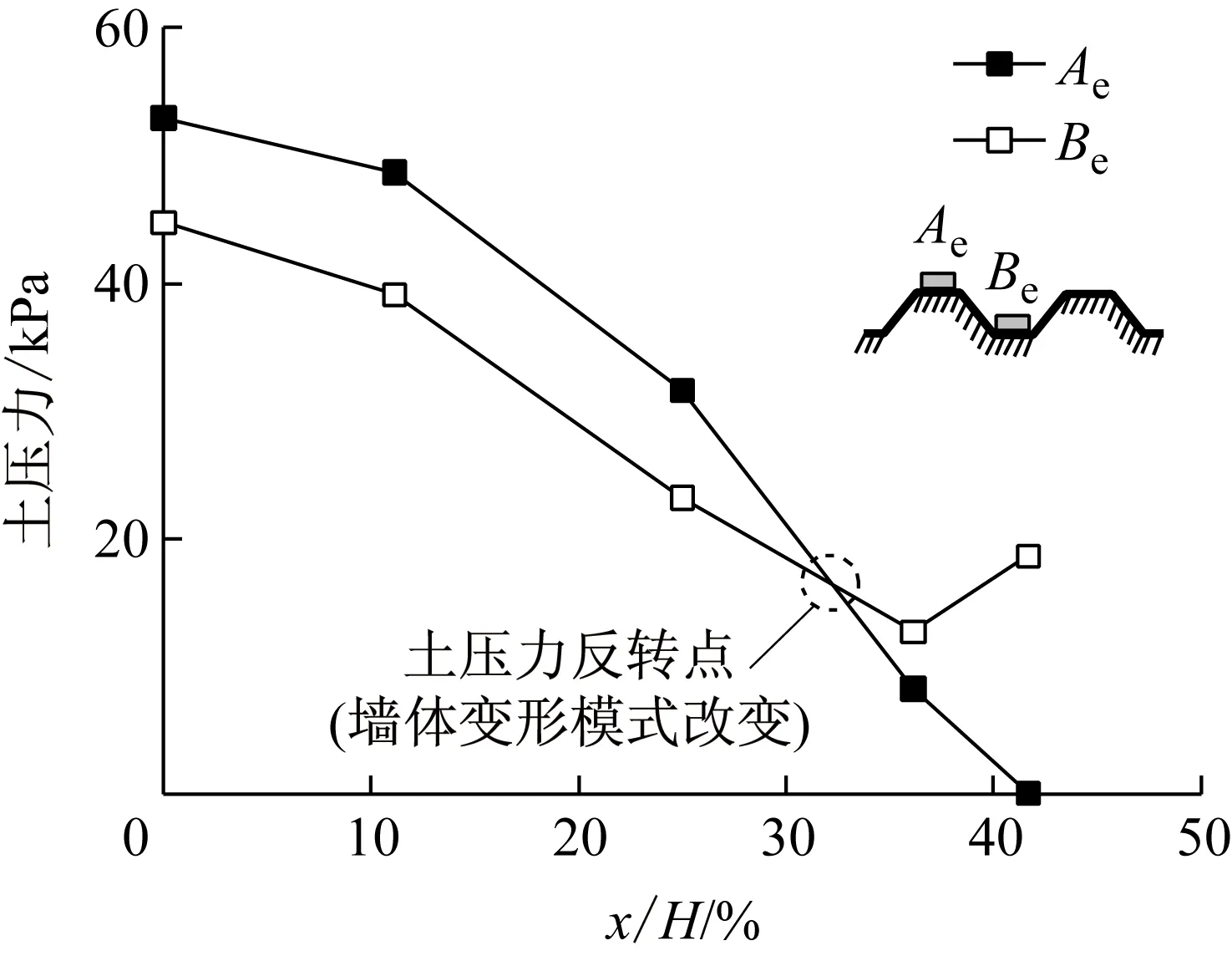
图7 埋深243.0 mm处开挖侧横向土压力分布

2.3.3与平板挡墙土压力对比

图9为相同高程处填土侧钢板桩挡墙土压力平均测值与平板挡墙的结果对比.埋深243.0 mm处，前者测值远小于后者，这可能是由于挡墙埋设方式不同引起的.钢板桩是固结后插入土体，平板墙由于厚度较大，采用了黏土固结前预埋.墙体埋设方式的区别对初始土压力影响较大，但随着开挖深度增加，墙体和土体变形协调之后，墙体埋设方式的影响逐渐减小，2组试验在相同高程处所测得土压力测值大致趋近主动土压力.埋深160.0 mm和85.0 mm处，钢板桩挡墙土压力的初始平均测值与平板桩比较接近，因为黏土层较软，钢板桩挡墙的插入阻力远小于砂土层，对软土层的土体扰动不如砂层明显；在整个开挖过程中，钢板桩挡墙的土压力变化曲线和平板墙土压力变化曲线大致平行，前者略低；这与前文述及的T-H试验的地基孔隙比较小、固结度较高的结论是一致的.

图8 填土侧横向土压力分布

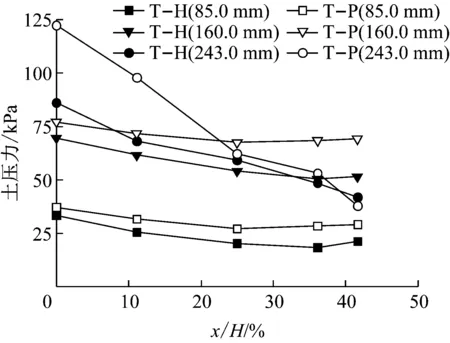
图9 不同试验中填土侧平均土压力对比

Fig.9Averagedearthpressuresmeasuredontheretainingsideofthewallsfromtwodifferenttests

3 关于形状效应机理的讨论

由上述分析可见，即使高程相同，钢板桩挡墙凹凸处的土压力值也不尽相同，这种差异的产生机理如图10所示.当墙体远离土体运动时(见图10a)，由于墙体与土体的刚度差异，墙体迎土面凸出部位的土体(2区)变形较大，其相对速率vr指向墙体，因此受到临近1区土体对它的剪力f(方向远离墙体)，导致2区墙后土压力减小；相反地，墙体迎土面凹陷部位后面的土体(1区)墙后土压力增加.因此，当墙体远离土体运动时，墙体迎土面凹处土压力大于凸处，即pa1>pa2；反之(见图10b),凹处墙体土压力小于凸处，即pa1

a 墙体远离土体运动

b 墙体靠近土体运动

图11给出了钢板桩模型挡墙在开挖过程中可能的变形示意图.当开挖深度较小时，墙体上部产生向坑内的弯曲变形，下部向坑内有细微位移.在开挖侧的测点处(埋深243.0 mm)，墙体靠近开挖侧土体运动，开挖侧迎土面凹处土压力测值小于凸处，如图7所示，当开挖深度小于30%H时，Be测点土压力曲线在Ae测点的曲线下方.但随着开挖深度增加，上部墙体向坑内变形显著增加(见图3)，墙体产生绕接近墙底某点的转动，导致墙体下部向坑外产生变形.此时，在开挖侧测点处(埋深243.0 mm)，墙体远离开挖侧土体运动，开挖侧迎土面凹凸处的土压力大小关系发生反转(见图7虚线所示的反转点).如图8所示，钢板桩挡墙填土侧的土压力值变化规律也大体一致，反映了墙体变形模式变化对墙后土压力大小关系的影响.

Fig.11Variationofdeformationmodesofthesheetpilewallduringexcavation

4 结论

通过离心模型试验研究了帽型钢板桩挡墙和平板挡墙在基坑开挖过程中的土压力变化情况，着重分析了在开挖过程中钢板桩挡墙迎土面不同部位土压力差异及变化规律，探讨了钢板桩挡墙土压力分布的形状效应产生机理.主要结论如下：

(1) 平板挡墙和钢板桩挡墙土压力在基坑未开挖时接近静止土压力分布，随着开挖进行，填土侧土压力逐渐减小并靠近主动土压力值.

(2) 由于挡墙埋设方法的差异，砂土层中平板挡墙和钢板桩挡墙后的初始土压力有所差异，这种差异随开挖深度增加而减小；当开挖深度较大时，在相同高程情况下，钢板桩墙体的平均土压力值与平板墙的土压力值大致相近.

(3) 相同高程处钢板桩挡墙凹凸部分的土压力不相等，大小关系与钢板桩位移模式有关.当墙体远离土体运动时，迎土面凹处土压力大于凸处；反之凹处土压力小于凸处.

(4) 钢板桩挡墙的墙顶变形随着开挖深度增加而增加，当开挖深度较小时，墙体整体向坑内变形；当开挖深度继续增加时，墙体产生转动，墙体上部向坑内变形，下部向坑外变形.墙体变形模式的变化引起钢板桩挡墙土压力在相同高程处的横向分布也产生变化.

致谢

感谢日本新日铁住金公司(Nippon Steel & Sumitomo Metal Corporation)的Nakayama Hiroaki博士、Taenaka Shinji博士和Kato Atsushi工程师对试验方案和数据分析的有益建议.清华大学张嘎教授、同济大学马险峰副教授、吴晓峰工程师、孙长安试验技师和曹培工程师对本研究给予了试验指导，康奇和刘宇泰同学协助完成了离心模型试验.