桥梁拉索金属面积损失的磁通检测信号特征

2018-11-02辛荣亚张启伟李元兵

同济大学学报（自然科学版） 2018年10期

辛荣亚，张启伟，李元兵

(同济大学土木工程学院，上海 200092)

拉索是桥梁中的承重构件，也是易损构件.文献[1]在对世界范围内多座斜拉桥考察后认为，除非桥梁拉索的腐蚀得以阻止，否则，许多斜拉桥有突然垮塌的危险.拱桥中的吊杆、系杆以及悬索桥主缆[2]同样面临着拉索钢丝的锈蚀与断丝问题，因钢丝锈蚀或断丝引发的桥梁断索事故也屡有报道[3].无损检测技术对于及时发现索体内的钢丝损伤并据此制定科学合理的维修管养策略至关重要.

磁性检测是目前最具潜力的桥梁拉索无损检测技术[4-5]，在索支承桥梁的现场检测中，可检出吊杆中的断丝与锈蚀病害[6].在磁性检测中，钢构件的缺陷可根据构造特点与检测方法的不同分为两类：①局部缺陷(local fault,LF型)，主要包括钢丝断丝、坑蚀和局部形状异常等，采用漏磁法进行检测；②金属截面积损失(loss of metallic cross-section area,LMA型)，指造成索体钢丝横截面积减小的损伤，如磨损与整体锈蚀，采用磁通法进行检测.现代化的磁检测设备中通常会同时集成漏磁检测元件与磁通检测元件[7-8].

由于漏磁信号与断丝截面积、断口宽度、位置、和断口形状之间呈非线性关系[9]，目前绳索类构件的漏磁检测主要可实现损伤的定性判别与定位[10-13].文献[7]认为漏磁信号反映的是钢丝有效横截面积沿轴向的变化速率，难以用作损伤定量识别，损伤的定量识别应采用磁通量信号.文献[9]指出当断口宽度大于某一临界值时，断丝缺陷可以在磁通量信号中显示出来.因此，磁通检测对于索体中锈蚀与断丝病害的定量识别有重要作用.

磁通检测的原理为：测试时使用永磁体或通电线圈进行励磁，永磁体或线圈与磁轭、钢丝构成磁回路，将钢丝磁化至饱和，通过测试磁回路中的磁通量来判定磁回路范围内钢丝的锈蚀情况，随着设备沿索体的行走和扫描完成全部钢丝的检测.钢材属于铁磁性物质，其磁导率远高于拉索中的其他材料，钢材发生锈蚀后，其磁导率急剧降低，锈蚀物对于回路磁通量几乎没有贡献[14].由于索体中的锈蚀、断丝、缺丝病害引起的磁通量信号相似，钢丝的锈蚀率也可称为更具广泛意义的钢丝截面损失率.对于较长范围内的钢材截面损失，文献[5]基于磁路分析指出回路磁通量变化量与截面损失率呈线性关系，并设计试验进行了验证.钢丝的截面损失率可通过回路磁通量进行定量识别.文献[15]在钢丝绳的检测中发现，磁通量信号的幅值不仅与截面损失率有关，还会受到钢丝锈蚀范围的影响；在锈蚀范围较小时，磁通量信号幅值偏小.为简便计，磁通量信号幅值受缺陷长度的干扰而削弱的规律可称作缺陷长度效应.在拉索的磁性检测中，拉索因护套破损引起的钢丝锈蚀常集中在破损区域，锈蚀范围对于磁通量信号量值的影响很可能会造成钢丝锈蚀率的误判.由此可知，研究短缺陷引起的磁通量信号的特征对于LF型缺陷和LMA型缺陷的定量评估均有重要意义.

针对桥梁拉索中锈蚀与断丝病害引起的金属面积损失，对磁通检测信号随缺陷参数的变化规律尤其是缺陷长度对于磁通检测信号的影响进行研究.基于磁路分析理论论证缺陷长度效应的存在机理及主要影响因素，采用模型试验研究磁通信号特征、验证理论分析的结论，并基于三维电磁有限元模型分析缺陷长度效应对于缺陷形态、截面损失率、索径、检测设备尺寸等参数的敏感性.

1 磁通检测的理论分析

1.1 磁回路的简化分析

磁通检测的简化分析可采用等效磁路法[5,13]进行.检测时磁感线的传播路径可简化为图1所示，其中路径①为有效磁通，其余为漏磁通.由于钢丝与磁轭的磁导率远大于空气磁导率，而且在一个设计合理的磁检测设备中，磁轭不会在钢丝之前达到磁化饱和，因此路径⑥中的磁通量很小，与其他路径相比可忽略不计.将图1中的磁回路等效为图2中的电路图，对此进行分析，由磁路中的欧姆定律可知

(1)

由方程组可解得

φ2=F/(Ra1+ARy+ABRc)

(2)

式中：Ra1为磁头与索体间空气隙的磁阻；Ra2为路径②～④的等效磁阻；Ra3为路径⑤中与索体平行段的空气磁阻；Rc为拉索的磁阻；Ry为磁轭的磁阻.φ1，φ2，φ3，φ4和φ5分别为通过永磁体、磁轭、拉索、Ra2和Ra3的磁通量；F为永磁体的磁动势.令A=1+Ra1/Ra2，B=Ra3/(Ra3+Rc)，由于钢丝的磁导率远大于空气，Ra3>>Rc，B≈1，式(2)可简化为

φ2≈F/[Ra1+A(Rc+Ry)]

(3)

钢丝的截面损失率与磁轭中的磁通密度呈线性正相关[5]，因此磁轭中磁通量的变化值与钢丝的截面损失率成正比.式(3)表明，截面损失率与缺陷长度对磁通量的影响主要通过索体磁阻Rc体现.

Fig.1Magneticinductionlineinthemagneticfluxexaminationsystem

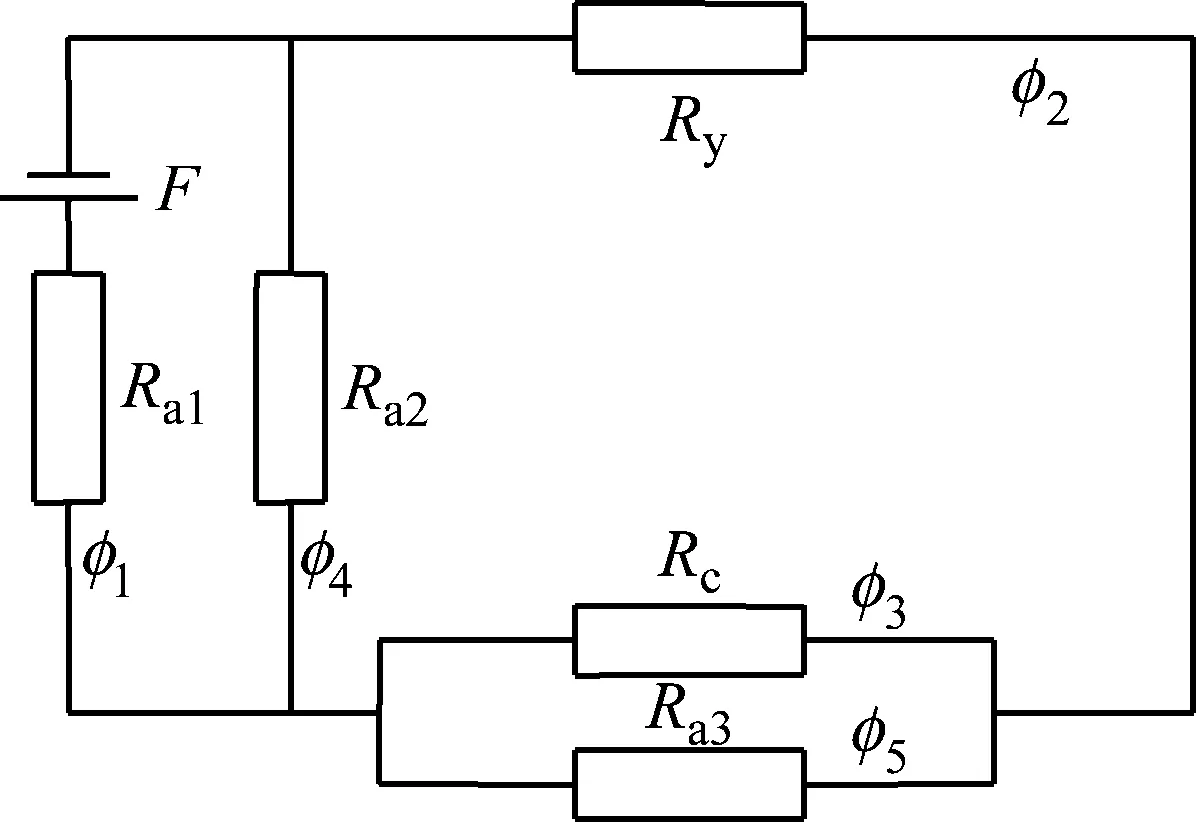
图2 等效磁路

1.2 缺陷长度的影响

式(3)中索体的磁阻与缺陷长度有关，为方便量化分析，将磁通路径①划分为4部分(见图3)：磁轭区、空气缝隙(Ⅰ区)、过渡区(Ⅱ区)、索体均匀磁化区(Ⅲ区).图3中，L0为磁轭长度，Lmag为永磁体长度，Lcr为永磁体间的净距，L为缺陷长度，g为永磁体与索体钢丝间的缝隙厚度.假定：

(1) 无缺陷时，Ⅲ区磁感应强度为均匀分布.

(2) 在缺陷较小时，Ⅱ区的磁阻为常数.

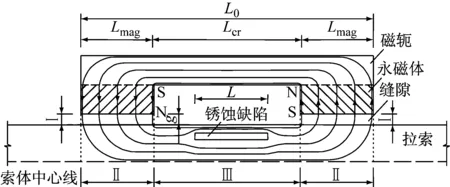
图3 检测系统磁回路示意

根据缺陷长度的不同，式(3)中Rc的计算可按以下4种情形考虑：

(1) 索体钢丝完好.记μc为拉索钢丝的相对磁导率，Sc0为钢丝的横截面积，则索体磁阻为

(4)

(2) 缺陷长度L≤Lcr.根据前述假定，仅索体磁阻发生变化，记钢丝的截面损失率为α，则索体磁阻为

(5)

(3) 缺陷长度L≥L0.若缺陷发生在内层钢丝上，可近似按式(5)计算索体磁阻，但取L=Lcr.通常情况下拉索钢丝的锈蚀程度由护套向索体中心逐渐减轻[16]，若假定锈蚀全部发生在外层钢丝上，此时索体的磁阻仍可按缺陷在内层钢丝上计算，但由于钢丝锈蚀后磁导率接近空气，磁头与钢丝间的缝隙磁阻增大，式(3)中Ra1与A均增大.即，缺陷在外层钢丝上时，磁回路中的总磁阻大于缺陷在内层时的总磁阻.

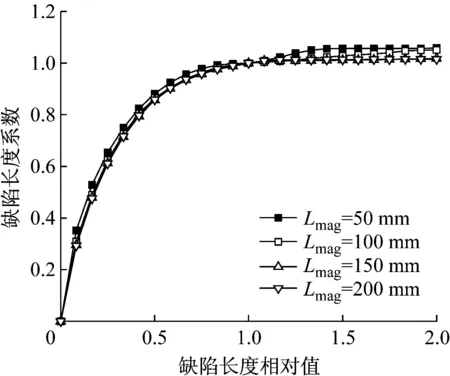
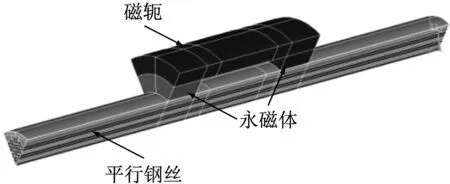
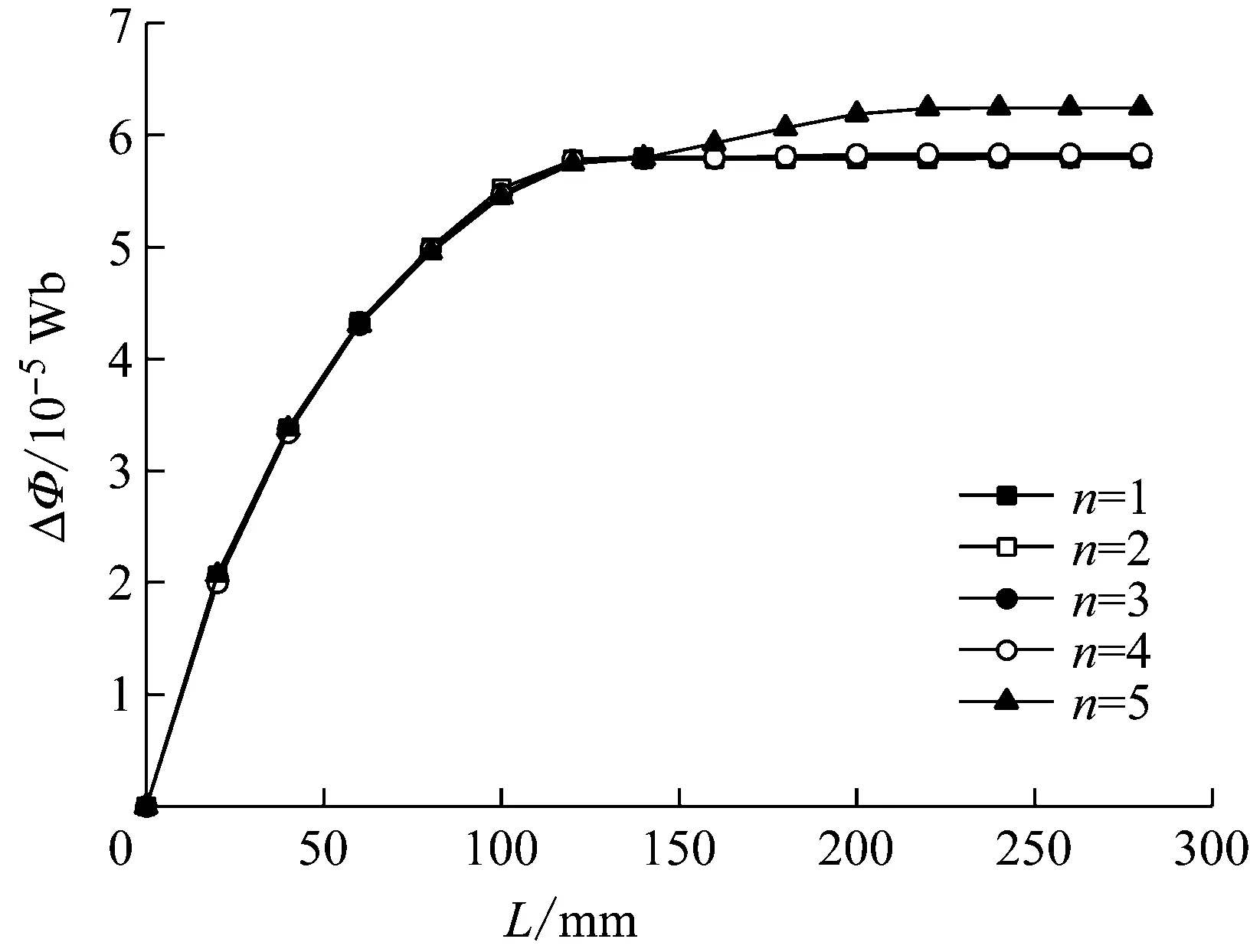
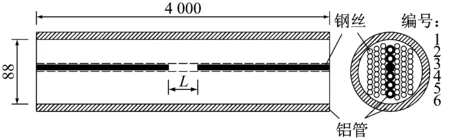
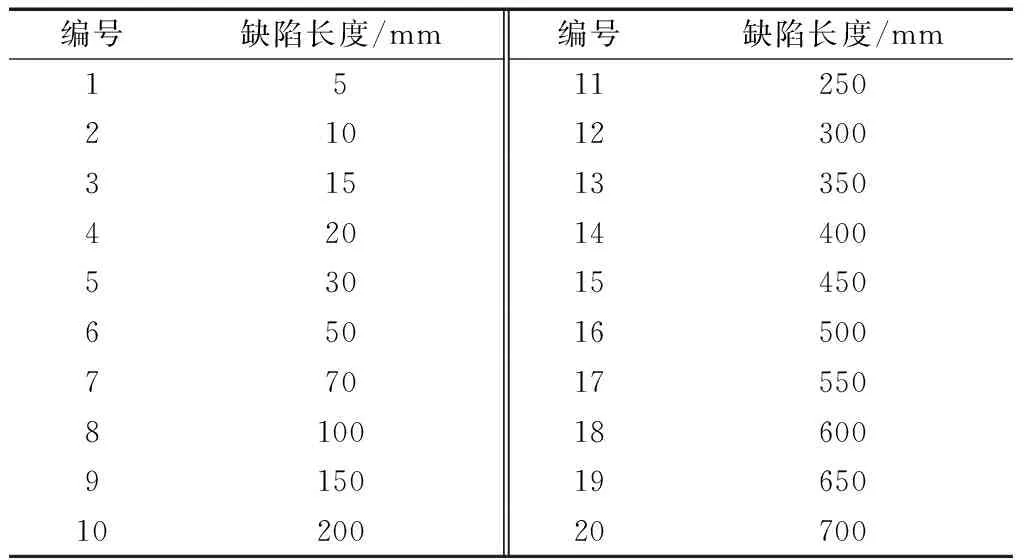
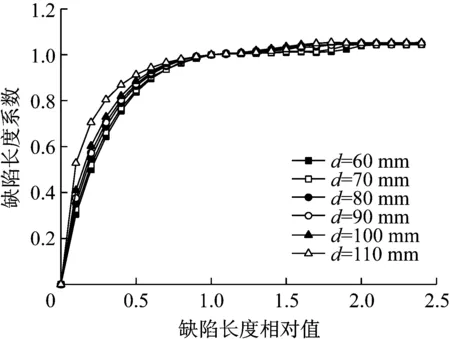
(4) 缺陷长度满足Lcr

记缺陷长为L时回路中的总磁阻为RL，RL=Ra1+A(Rc+Ry)，假定缺陷位于外层钢丝上，则RL随L先由R0=RL(L=0)线性增加至Rcr=RL(L=Lcr)，再增加至RL0=Rcr+ΔR，之后保持不变.其中ΔR为Ra1增大引起的总磁阻增加，显然ΔR与α有关，且随α的增大而增大.

1.3 缺陷长度系数

拉索的磁通检测中最值得关注的是截面损失率，其与磁轭中的磁通量变化近似成正比.为便于表述磁轭中磁通量随钢丝缺陷长度的变化规律，选取缺陷长度为Lcr时引起的磁通量变化为基准，通过磁通量变化的相对大小来揭示缺陷长度的影响规律.把长L的缺陷引起的磁通量变化与长Lcr的缺陷引起的磁通量变化的比值记作f(x)，称为缺陷长度系数.f(x)可写作下式：

(6)

式中:x=L/Lcr，为缺陷长度相对值；ΔΦL，ΔΦcr分别为长度为L的缺陷和长度为Lcr的缺陷引起的磁通量变化值；R0为无缺陷时磁回路中的总磁阻.由式(6)和分析可知，当L≤Lcr时，RL随L线性增加；f(x)随L非线性增加，曲线f(L)的线型可近似看作双曲线.Lcr

2 短缺陷的磁通量信号特征

由于钢丝的磁化过程为非线性，基于理论公式仅能对缺陷长度的影响做定性分析.有限元方法经济成本低而计算精度高，被广泛用于无损检测中电磁场的模拟与检测设备的优化设计[17-18]，所以采用有限元模拟和模型试验对理论分析的结果进行检验和补充.

2.1 有限元模型的建立

使用通用有限元程序ANSYS对拉索的磁性检测过程进行非线性分析，采用SOLID96单元建立1/6三维有限元模型(图4)，模拟φ7-61拉索钢丝中的LMA缺陷.钢丝磁化曲线采用1670-φ7 mm镀锌钢丝的实测值，永磁体采用钕铁硼N35材料，磁轭采用相对磁导率为1 000的纯铁.由于钢丝锈蚀后化学成分发生变化，且碎屑的形态会产生较强的退磁效应，锈蚀物的宏观磁导率远小于钢丝的磁导率且与空气接近[14].此外，拉索护套与防护油脂等属于非铁磁性材料，因其磁导率与空气接近(约为钢材的1/500～1/300)，所以对磁通检测信号无影响.模型中对护套与钢丝缺陷赋予空气的材料属性，即它们的相对磁导率取为1.

图4 平行钢丝电磁有限元模型

模型中永磁体内侧直径为75 mm、厚20 mm、长40 mm；磁轭厚20 mm、长200 mm；钢丝建模长度取800 mm.电磁分析中采用差分标量势法求解，模型边界采用自然边界条件.考虑到磁场耗散的影响，为确保计算精度，模型外围设置约7倍索体直径的空气单元(为便于观察，图4中未显示外围空气).

2.2 磁通量信号沿索体纵向的变化规律

基于图4中的有限元模型，模拟仪器对索体的扫描过程.设定有1根钢丝发生锈蚀或断丝(α=9.84%)，以磁轭中心的磁通量代表检测信号，模拟多组长度的缺陷，信号波形见图5.由图可知：沿索体纵向扫描得到的磁通量信号在缺陷的中心位置形成波谷；随着缺陷长度增加，信号谷值降低并在波谷形成平台后保持不变；信号宽度随缺陷长度的增加呈线性增加.

图5 钢丝缺陷的磁通量信号

在定量评估中通常依据LMA型缺陷引起的磁通量变化量(ΔФ)的最大值进行截面损失率计算，为此将ΔФ的峰值列于图6.图中，短缺陷(LLcr)的情况.显然，损伤评估时若不考虑缺陷长度对于磁通量信号的影响，截面损失率将被低估.拉索钢丝共5层，图6中，n=1～5分别代表中心层钢丝至最外层钢丝的序号.由于有限元模型为1/6模型，图6中n=1时的数据已放大6倍再与其余组进行对比.n=1～4时，各层钢丝的锈蚀缺陷引起的ΔФ随L的增加先沿上凸曲线增加，在L达到一个临界值Lcr(此处为120 mm)后达到最大值ΔФcr并保持不变.对于n=5，ΔФ进一步增加，并在L达到磁轭长度后保持不变.磁通量变化量随缺陷长度的变化规律与理论分析中得出的结论相吻合.n=1～4时数据的高度一致性说明：无论缺陷长短，磁通量变化值均与截面损失率成正比；除表层缺陷外，缺陷径向部位对磁通量信号几乎无影响.表层缺陷的特殊性在于，当缺陷长度介于Lcr和L0之间时，内层钢丝锈蚀引起的磁阻不发生变化；而表层钢丝锈蚀会使得式(3)中的Ra1与A增大，进而增大磁回路中的总磁阻.

图6 磁通量信号变化值

2.3 模型试验布置

为对磁通量随缺陷长度的变化规律作进一步验证，制作拉索模型进行磁通检测.拉索模型示意见图7，模型中使用了66根直径为7 mm的高强钢丝，钢丝放置在内径为88 mm、厚为10 mm的铝管中.铝为顺磁性物质，相对磁导率约为1.000 02[19]，接近空气；而钢丝为铁磁性物质，相对磁导率约为铝的500倍，因此铝管既可作为钢丝的支撑框架又不会干扰磁性检测信号.铝管中另设6根内径为8 mm的小铝管作为高强钢丝自由滑动的轨道，通过钢丝的滑动和拼接可模拟各种长度的LMA缺陷.

图7 拉索模型示意(单位: mm)

拉索模型的磁通检测采用波兰LRM-MH120钢丝绳诊断系统，设备中磁轭长L0=300 mm，磁头长Lmag=50 mm，相应地，Lcr=200 mm.拉索模型的面积损失率设定为3.03%(即为2/66)，使用2根钢丝进行模拟,改变钢丝在小铝管中的位置来模拟不同长度或部位的缺陷,共计60种.对每种缺陷进行1次扫描测试，共计60次测试.缺陷按照部位的不同分为3组：第1组位于铝管1和铝管6中，模拟外层缺陷；第2组位于铝管2和5中，模拟中层缺陷；第3组位于铝管3和4中，模拟内层缺陷.对于每组缺陷，缺陷长度均有20种，见表1.考虑到设备自身长度，设备在拉索模型上可自由行走的距离约为2 m.

表1 各组LMA缺陷的长度

2.4 模型试验结果

磁通量测试信号按照0.25 cm的间隔进行等空间采样，信号的横坐标与扫描过的索体长度一一对应.通过对比拉索模型中有缺陷时的磁通检测信号和无缺陷时的检测信号可得缺陷引起的磁通量变化信号，对信号进行小波降噪后可提取其幅值ΔФ进行截面损失率评估.无缺陷时磁通信号在零值附近(受噪声影响会有轻微波动)，有LMA缺陷时磁通信号在缺陷位置出现凹陷，凹陷长度略大于缺陷长度且随其增加而等量增加(见图8a、图5).磁通信号在时域上直接反映了钢丝横截面积的变化，而信号在频域无明确物理意义，在损伤评估中仅关注其时域特征，并根据信号凹陷的最大量值判定损伤程度.缺陷较长时，信号凹陷的量值一般认为与截面损失率成正比[5].

测试结果表明，对于长度L>Lcr(200 mm)的长缺陷，缺陷引起的磁通量变化值与L无关(见图8a、8b)，图8b中各层长缺陷的ΔФ的离散性由随机误差引起.通过对各层缺陷的ΔФ分别计算平均值发现，缺陷引起的ΔФ受缺陷径向位置的影响，其数值从外层到内层近似按线性变化递减至84.6%左右.

a 典型磁通量信号波形(外层缺陷)

b 磁通量信号幅值(L>Lcr)

c 缺陷长度系数(L≤2Lcr)

Fig.8Measuredmagneticfluxsignalandthedefect-lengthfactor

这说明外层钢丝对内层钢丝有磁屏蔽作用，使得钢丝的磁化强度沿拉索径向近似按线性衰减，衰减的比例约为15.4%.

图8b中给出了所有长缺陷的ΔФ，由前文的理论分析可知，对于较短的缺陷，其引起的ΔФ将受到缺陷长度的影响.为了更清晰地观察这一影响，对短缺陷的ΔФ作如下处理：①按式(6)计算实测的缺陷长度系数(见图8c)，以便于和理论分析对比；②计算时，内层、中层和外层缺陷分开进行，以剔除外层钢丝磁屏蔽的影响；③计算中的ΔФcr取长缺陷(L>Lcr)的ΔФ的平均值，以减小随机测试误差的影响.为便于观察短缺陷的缺陷长度系数，图8c中仅显示L≤2Lcr的结果.实测数据表明：缺陷长度系数与缺陷部位无关，在内层、中层与外层的数值基本相同；缺陷引起的ΔФ在L

缺陷长度系数f(x)随缺陷长度L的变化规律可采用如下函数对实测数据进行拟合：

(7)

边界条件设为f(1)=1，根据试验数据拟合得到a=1.286 6，b=-0.405 1，c=0.413 7.图8c中拟合效果良好，说明f(x)的线型可看作双曲线，与理论公式(6)推演出的结论相符.对于特定的检测设备，可取几组不同长度的缺陷进行磁通量测试后使用双曲线拟合得到完整的f(x)曲线.

3 基于有限元的参数敏感性分析

前文揭示了缺陷长度对磁通量信号的影响规律，其影响的程度还可能和缺陷分布形态、截面损失率、待检测索体的直径、检测设备尺寸等因素有关，需要进一步研究各参数的敏感性.采用模型试验对这些因素开展研究在实际中很难实施，因此，基于有限元法进行参数敏感性分析.为节省模型求解时间，将图4有限元模型中的平行钢丝简化为同等横截面积的圆棒进行计算(见图9).计算中分别针对各个参数作敏感性分析，各参数的缺省值为：角度取60°，截面损失率α=10%，拉索直径d=80 mm，Lcr=300 mm，Lmag=100 mm.此外，计算中取永磁体内径D=120 mm.

图9 等效钢棒模型横断面示意

Fig.9Cross-sectionlayoutoftheequivalentsteel-barFEmodel

3.1 缺陷分布形态的影响

等效圆棒模型中缺陷形态的设定见图9.保持缺陷总面积不变，改变缺陷在横断面上分布的角度范围，计算缺陷引起的磁通量变化.图10中结果表明，在截面损失率相等的情况下，角度取10°～60°时磁通量的变化值相等，缺陷分布的形态对磁通量信号无影响.因此，在索体断面上，相同截面损失率的均匀锈蚀、非均匀锈蚀、断丝以及缺丝损伤引起的磁通量信号变化幅度是相同的.同时也在侧面印证了：将平行钢丝模型简化为圆柱体模型产生的误差可以忽略不计.

图10 各类缺陷形态下的磁通量变化

Fig.10Variationofthemagneticfluxfromdefectsofvariousmorphologies

3.2 截面损失率的影响

图11a中f(x)随α的增加而增大，与理论分析的结论相吻合，说明α越大，磁通量信号受缺陷长度的影响越小.不过，α对f(x)的影响整体较小，在L≥0.6Lcr时，不同α对应的f(x)值差异很小.此外，fmax通常不大于1.05，说明外层钢丝锈蚀与内层钢丝锈蚀引起的磁通量差异较小，在实际检测中可忽略不计.

需要注意的是，若将缺陷长度效应看作是线性的(如文献[8]中使用的简化处理)，则相同体积的短缺陷(Lx(01)，则缺陷长度减小为1/m,此时磁通量变化值与原来的比值为m·f(1/m)>m/m=1.因此，截面损失率对于磁通量变化值的影响程度总是大于缺陷长度对于磁通量变化值的影响程度，无论缺陷长度取值如何，缺陷体积相同时截面损失率越大缺陷引起的磁通量变化值越大这一规律总是成立.

a 截面损失率固定时的缺陷长度系数

b 缺陷体积固定时的磁通量变化

Fig.11Influenceonthedefect-lengtheffectfromthepercentLMA

3.3 索体直径的影响

将索体内的钢丝等效为具有相同横截面积的圆柱体，圆柱体的直径d对于缺陷长度效应的影响见图12.由图可知，随着d的增大，f(x)的数值逐渐增加；当索体等效直径逼近检测设备内径时，缺陷长度效应明显削弱.此外，f(x)的最大值fmax随索体等效直径的增加轻微增加.文献[15]认为在钢丝绳检测中，当锈蚀率超过10%时，缺陷长度对磁通量信号的影响可忽略不计.图11中结果与这一观点不符，但可通过图12的结果分析造成差异的原因.钢丝绳的横断面接近圆形且无防护层，在实际检测中可采用内径与钢丝绳直径接近的检测设备；而且裸露的钢丝绳其锈蚀范围一般较大，缺陷长度效应较弱，因此，文献[15]中的观点对于钢丝绳的磁性检测是可以接受的.同理，在圆形钢棒的检测中缺陷长度效应更弱.而在桥梁检测中，拉索有防护层，且平行钢丝的排列方式接近正六边形，钢丝的等效直径显著小于索体的外径与磁头内径.由图12可知，当钢丝的等效直径较小时，拉索磁通检测中的缺陷长度效应随截面损失率增大而减弱的趋势轻微，缺陷长度效应显著，在缺陷定量识别中不可忽略.

图12 索体直径对缺陷长度效应的影响

Fig.12Influenceonthedefect-lengtheffectfromthecablediameter

3.4 检测设备尺寸的影响

对缺陷长度效应有影响的设备尺寸主要包括磁头内径、磁头间净距Lcr和磁头长度Lmag.由拉索的磁化过程可知，磁头内径的影响主要体现在与钢丝表面之间的缝隙上，其影响特点与索体直径相反.Lcr和Lmag对缺陷长度效应的影响见图13.图13a中，Lcr增加时缺陷长度系数f(x)随缺陷长度L变化的规律呈现显著波动，但不具有统一的波动规律.图13b中，Lmag增加时f(x)几乎不变，磁头长度对缺陷长度效应的影响较小，可忽略不计.因此，对于Lcr彼此不同的检测设备，需分别建立各自的缺陷长度系数曲线.进而可基于此曲线对拉索金属面积损失的评估结果进行修正[20].例如，当测得的截面损失率为αt时，可取修正值为α=αt/f(L).结合前文可知，对于特定的设备，选择其适用范围内索径最小的拉索建立有限元模型并设定较小的截面损失率可得到一条数值最小的f(L)曲线，在后续的修正中得到略偏安全的评估结果.

4 结论

(1) 桥梁拉索的磁通检测信号波动值与截面损失率成正比，同时还可能受到缺陷长度的干扰.决定缺陷长度L是否对磁通检测信号产生影响的临界值主要为磁头间净距Lcr：当L≤Lcr时，缺陷引起的磁通量变化值随L的增加沿上凸曲线增加，且线型可近似看作双曲线；当L>Lcr时，内部缺陷引起的磁通量变化值不再变化，而外部缺陷引起的磁通量变化值略有增加，并在L超过磁轭长度后保持为常数.