二氧化碳扩散系数的实验研究和模型计算

赵光华

(长城钻探工程技术研究院，辽宁 盘锦 124001)

二氧化碳(CO2)吞吐可以用于多种条件的油藏[1]，如粘度不太高的稠油油藏，水驱油藏(稀油)高含水时期，油层连通性差、非均质严重、无法形成注采系统的小断块，块状、具有顶部剩余油的倾斜油层等。中原油田胡12块属于非均质严重的中高渗透油藏[2]，注水效果差，现场试注N2驱油效果不好，目前已进入高含水阶段，急待推广应用CO2吞吐采油技术。大量研究表明，分子扩散是CO2提高原油采收率的一个重要机理[3-4]。因此，在高压和不同温度下，CO2在原油中的扩散系数是决定CO2在原油传质速率的一个很重要的参数。由于地层基岩很复杂 ，注入的CO2很难与油藏中原油完全混合好[5]。多数情况下，CO2通过分子扩散溶于原油，当水相将油相与CO2气相隔开时，水相阻碍了CO2分子的扩散，并且完全抑制了轻质烃类化合物释放到CO2中。然而，当CO2气体连续注入时，CO2的分子扩散能够通过水层将残余油驱替，从而提高原油采收率。

气体在原油中扩散系数的实验测定方法可大体归纳为传统方法和非传统方法。传统方法主要是测定气体在不同时间的组成(气相色谱[6]或核磁共振[7])，得到扩散系数。非传统方法建立在测定由分子扩散造成的气-液体系某一性质的改变，包括溶质的挥发速率[8]、气体体积[9]、折射率[10]、毛细管内原油-气体的界面位置[11]、气体包围下悬油滴的形状[12]及体积[13]等。本文采用动态界面张力法测定CO2在原油中的扩散系数，相对于其他实验方法，该方法具有操作时间短、恒压恒温下通过测定的动态界面张力值就能同时计算出扩散系数和界面传质系数等优点。本文的研究对象为中原油田胡12块轻质原油。

1 模型基础

图1(a)描述了在某一温度、压力下一个形状完整的悬油滴。图1(b)为周围分布CO2的轴对称悬油滴示意。注射探针的内径用rn表示，注射探针壁厚用εn表示，注射探针高度用hn表示，悬油滴包括探针内部的油相用ω表示，注射探针顶部的切平面和探针及原油形成的界面用φn表示。

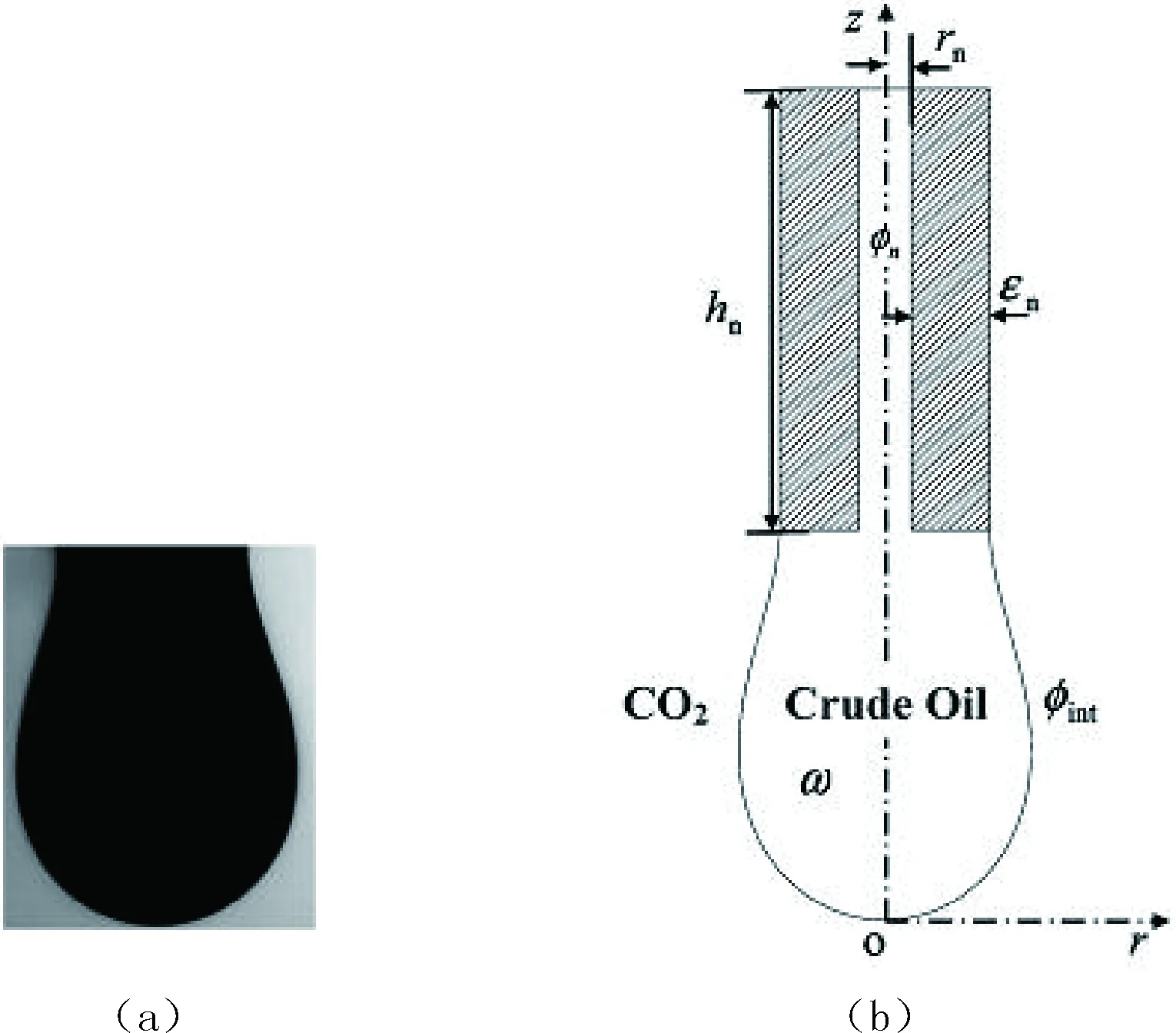
图1 (a)一个完整悬油滴的数码图像；(b)圆柱坐标体系(r，z)下轴对称悬油滴在CO2相中示意

本次研究中，悬油滴形状和体积的改变对扩散过程带来的影响可以忽略。假设扩散过程中悬油滴是静止的，根据Ghez的气体扩散理论[14]，用于描述CO2在悬油滴内部(包括注射探针内部油相)的浓度转移扩散公式可以表示成:

(1)

式中，D为CO2在原油中的扩散系数，m2/s，假设它与CO2的浓度无关。

在传质过程的开始阶段，悬油滴内部CO2的浓度为0，因此，公式(1)的初始条件为[14]：

c(r,z,t)|t=0=0,(r,z)∈ω

(2)

注射针壁及切平面对于CO2来说是不可渗透的，相应的非渗透边界条件为：

(3)

式中，nr和nz为方向余弦，即注射探针和原油以及切平面形成界面的单位矢量在r轴和z轴形成的分量。

本次研究考虑CO2通过原油-CO2界面的界面阻力，因此，非平衡边界条件应用于界面得到[14]：

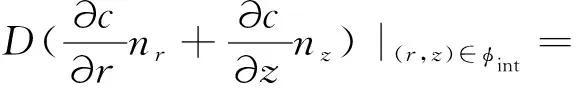
(4)

式中，k为界面传质系数，m/s，ceq为CO2在指定压力和温度下在原油中的平衡浓度，mol/m3。

公式(1)～(4)可以通过引进4个无量纲变量和1个无量纲参数将其无量纲化：

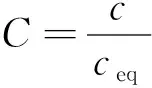
(5)

式中，C为CO2的无量纲浓度；R和Z为无量纲的径向和轴向坐标；rn为注射探针的内径；τ为无量纲时间；kD为传质Biot数；实际上，传质Biot数表示本体阻力rn/D与界面阻力1/k的比值[15]。

本次研究应用半离散Galerkin有限元素法来解决上述无量纲公式,具体的数学处理过程可以参照文献[16]。

悬滴在t=0的第一个数码图像用来定义每个压力下的传质模型的物理范围ω，如图1(b)所示。然后，扩散公式(1)连同公式(2)～(5)是通过采用半离散Galerkin有限元素法得到CO2在计算域Ω下的无量纲浓度转移C(R,Z,τ)和CO2在界面处的平衡浓度Cint(τ)。CO2的平均无量纲界面浓度能够转换成真实时间t下浓度Cint(t)。本次研究中，假设动态界面浓度和动态界面张力的关系遵循平衡界面浓度和平衡界面张力的关系[17]，CO2在原油中的平衡浓度(溶解度)可通过Simon-Graue关系式[18]计算出。那么，动态界面张力就能够通过计算的动态界面浓度Cint(τ)计算出来。

用目标函数表示数学计算的动态界面张力和实验测得数据的偏差。令ti和γm(ti)，i=1,2,3,…,N是一组时间和实验测得的动态界面张力，tj和γc(tj)，j=1,2,3,…,K是另一组时间和理论计算的动态界面张力。这里，目标函数被定义为：

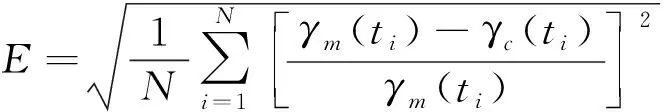
(6)

从公式(6)可以看出目标函数是计算和测得的动态界面张力的均方根相对误差。计算的动态界面张力随着计算的CO2界面浓度Cint(t)的变化而改变，而CO2在界面的浓度是由传质Biot数kD和扩散系数D共同决定的。因此，目标函数值是由传质Biot数kD和扩散系数D共同决定的。

E=E(kD,D)

(7)

一旦全局目标函数能够最小化，kD和D就作为真实的传质Biot数和真实的扩散系数。

本次研究采用一个参数同时查找方法，计算传质Biot数kD和D扩散系数的数学过程如下：

(1)周围分布CO2的悬油滴的连续数码图像能够得到，动态界面张力γm(ti)能够测得。

(2)悬油滴在t=0的第一个数码图像定义为传质模型的物理范围ω，如图1(b)所示。

(3)在一个给定的温度压力下，传质Biot数的11个测试点选为kD,i，i=0,1,2,…10。

(4)对于一个给定的kD,i，扩散公式(1)连同公式(2)-(5)是通过半离散Galerkin有限元素法得到CO2在计算域Ω中的无量纲浓度转移C(R,Z,τ)。

(5)对于一个给定的kD,i，扩散系数D有上下限[D0,D10]。

(6)D的初始不确定时间间隔被11个节点Dj,j=0,1,2,…10划分为10个等同的子区间。

(7)对于一个给定的Dj，无量纲时间τ能够转换为真实时间t。应用测得的平衡界面张力和计算的CO2平衡浓度的关系曲线，任何时间t下的动态界面张力就能够计算出来。利用测得和计算的动态界面张力，通过公式(6)得到相应的目标函数E(kD,i,Dj),j=0,1,2,…10。

(8)通过对比不同的E(kD,i,Dj),j=0,1,2,…10，局部最小目标函数就得到了Emin(kD,i,Dj)，1≤j≤9。然后，D的不确定间隔变为[Dj-1，Dj+1]。

(9)如果新的不确定间隔[Dj-1，Dj+1]足够小，能够满足扩散系数的代数精度要求，那么，Dj就作为给定kD,i的局部最佳值。否则，新的不确定区间[Dj-1，Dj+1]将作为D的初始区间重复步骤(6)～(9)，直到满足终止条件。

(10)对于所有的kD,i，i=0,1,2,…10，步骤(4)～(9)将重复进行。通过对比不同的E(kD,i,Dj),j=0,1,2, … 10，可得到局部最小函数Emin(kD,m,Dn)，1≤m≤9，kD,m和Dn就作为传质Biot数和扩散系数的最佳值。

(11)如果m=0或m=10，则kD,i，i=0,1,2,…10将重新被选取。对于一个新值kD,i，步骤(4)之后的数学最小化过程将重复进行直到满足1≤m≤9。

对于原油-CO2体系kD和D的查找范围为0.3～8.8和(0.01～10)×10-9m2/s。D的终止条件是︱Dn+1-Dn-1︱≤0.005×10-9m2/s。

2 实验部分

实验采用加拿大ROBINSON D B公司生产的JEFFRI高压界面张力仪，该实验装置如文献[19]所述，实验用CO2由北京氦普北分气体有限公司生产，纯度为99.95%。油样采用中原油田胡12块轻质原油，原油在300.15 K、常压下的密度和黏度分别为0.837 g/cm3和13.0 mPa·s。该原油的组成分析结果见表1。

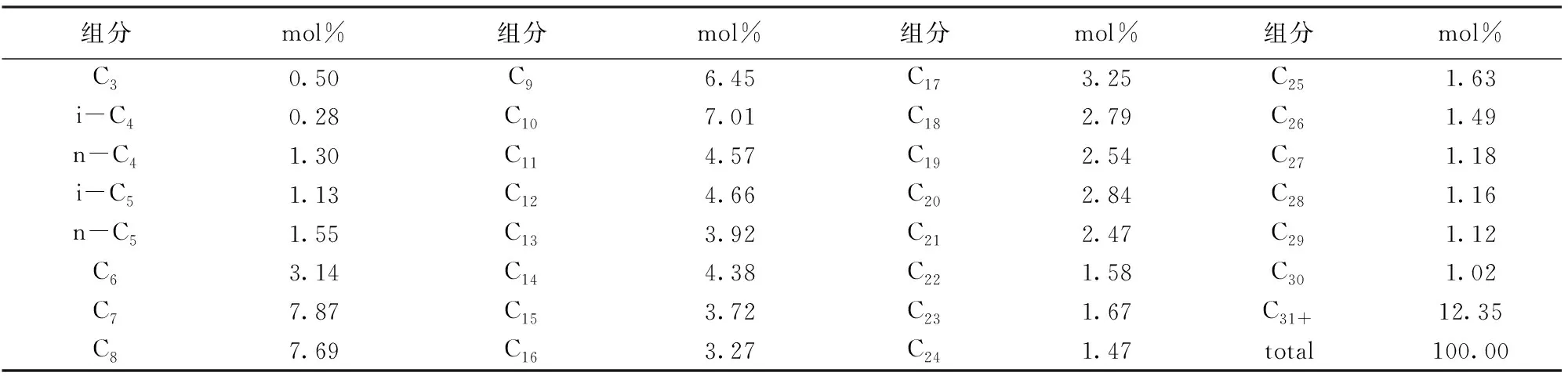
表1 中原油田胡12块轻质原油组成分析

C1～C6:7.90,C7+:92.10

本实验采用悬滴法进行界面张力测定。应用ANDREAS等提出的选面法[20]计算界面张力，实验方法在文献[19]中已作详细阐述。记录300.15 K，0.5～4.1 MPa下CO2在原油中不同时间下的悬滴图像并计算动态界面张力。

3 结果与讨论

3.1 动态界面张力与平衡界面张力

在300.15 K下，不同压力下动态界面张力随时间的变化如图2所示，动态界面张力随着时间的增大逐渐趋于一个稳定值，这个稳定值就定义为平衡界面张力。从图2可以看出动态界面张力随着压力的升高而降低，这是由于在高压下CO2在原油中的平衡浓度更高，能够有效降低原油的界面张力。

图2 300.15 K，不同压力下测得的动态界面张力(点)与计算的动态界面张力(线)随时间的变化

动态界面张力在高压下能够更快地达到平衡界面张力，5个不同压力下的平衡界面张力如图3所示。从图3可以看出平衡界面张力随着压力的升高而降低。通过Simon-Graue关系式[11]得出CO2在原油中的平衡浓度与压力的关系，见图3。

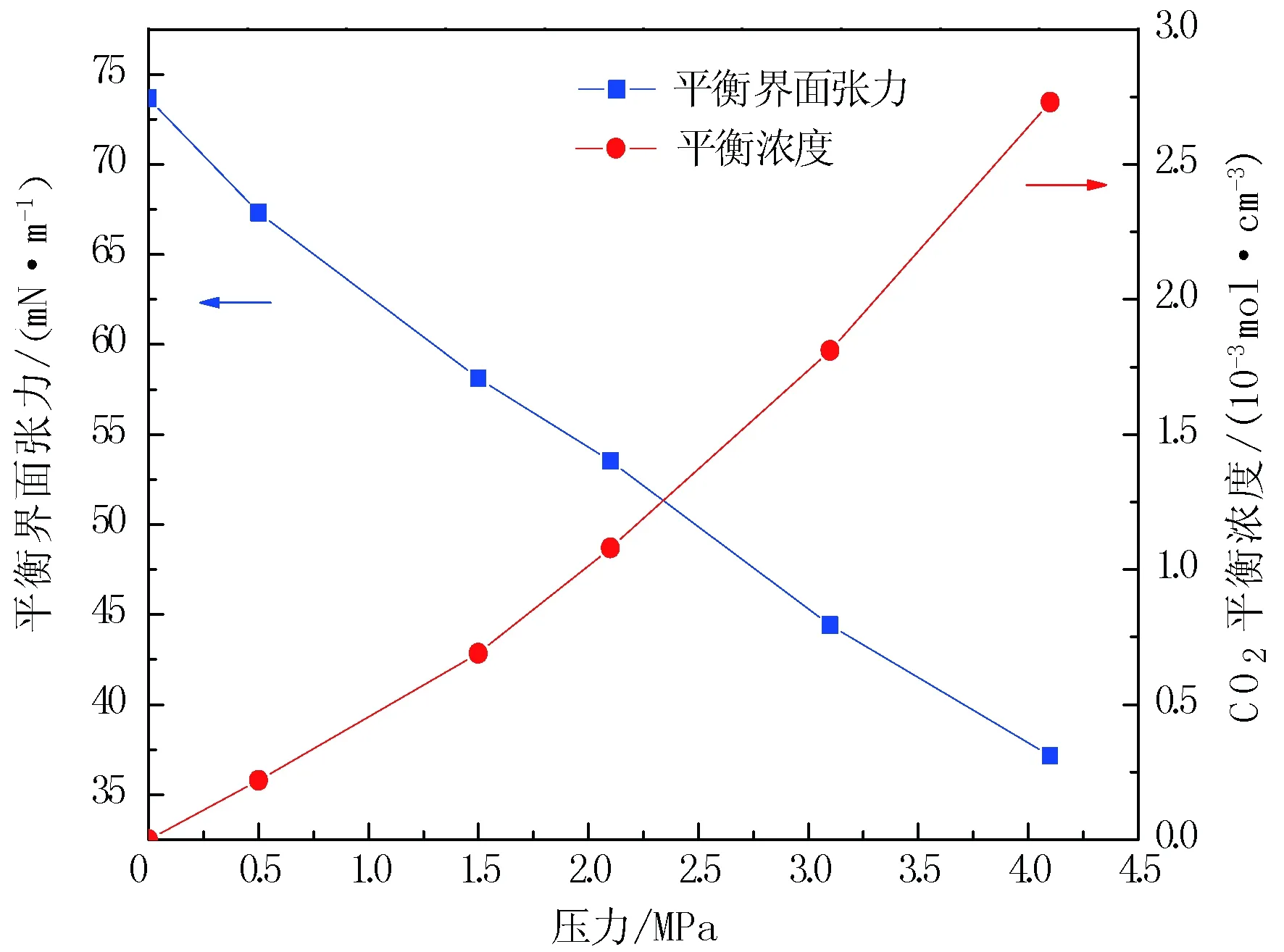
图3 300.15 K下，CO2在原油中的平衡界面张力、平衡浓度与压力的关系曲线

从图3可以看出CO2的平衡浓度随着压力的升高而增大。在300.15 K下，CO2在原油中的平衡界面张力与平衡浓度的关系见图4。图4就作为300.15 K下测得的平衡界面张力与CO2在原油中平衡浓度的关系曲线。

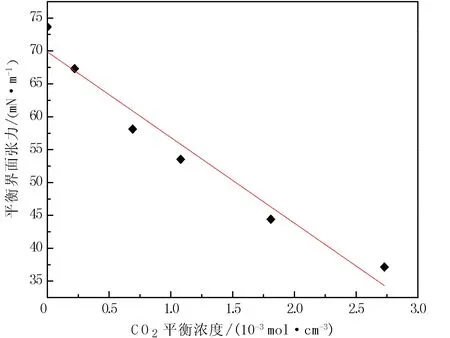
图4 300.15 K下，CO2在原油中的平衡界面张力与平衡浓度关系曲线

3.2 扩散系数和传质Biot数

通过测得的动态界面张力数值，目标函数E(D,kD)通过计算能够最小化，这样能够确定CO2在原油中每个压力下的扩散系数D和传质Biot数kD。在300.15 K，p=0.5 MPa下，原油-CO2体系在不同传质Biot数下的扩散系数D如图5所示，从图5可以看出，对于一个给定的传质Biot数，存在一个最佳扩散系数D使全局目标函数最小化。对于不同的传质Biot数，存在一对扩散系数D和传质Biot数kD最优值，能够使目标函数最小化。在300.15 K、p=0.5 MPa下，原油-CO2体系的最优扩散系数D=0.48×10-9m2/s，最优传质Biot数kD=4.0。

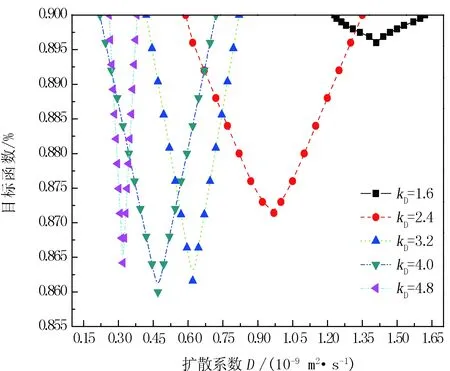
图5 300.15 K,0.5 MPa下不同传质Biot数下目标函数与扩散系数的关系曲线

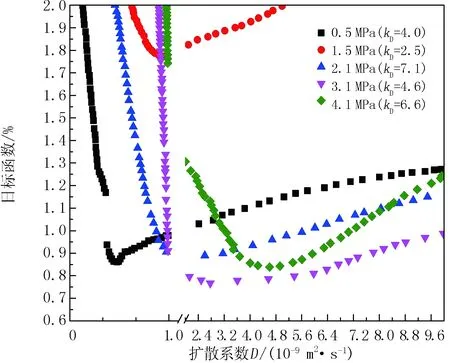
图6 300.15 K,0.5 MPa下不同压力下的全局最优传质Biot数下的目标函数与扩散系数的关系曲线

图6表示在p=0.5,1.5,2.1,3.1,4.1 MPa下，CO2的扩散系数D在全局最优传质Biot数下不同的目标函数E(D,kD)。从图6可以看出，每一条目标函数曲线都对应一个最佳扩散系数D，能够使目标函数最小化。此时，扩散系数D和传质Biot数kD就作为真实值。本次研究中，300.15 K，0.5～4.1 MPa下，扩散系数D的计算结果为(0.45～4.61)×10-9m2/s，传质Biot数为2.5～7.1，界面传质系数为(0.85～8.33)×10-5m/s。

300.15 K，p=0.5,1.5,2.1,3.1,4.1 MPa下计算出的CO2在原油中的平衡浓度、扩散系数、传质Biot数、界面传质系数以及全局最小目标函数Emin(D,kD)值见表2。

从表2可以看出，理论计算与实验测得的界面张力均方根相对误差低于1.81%。

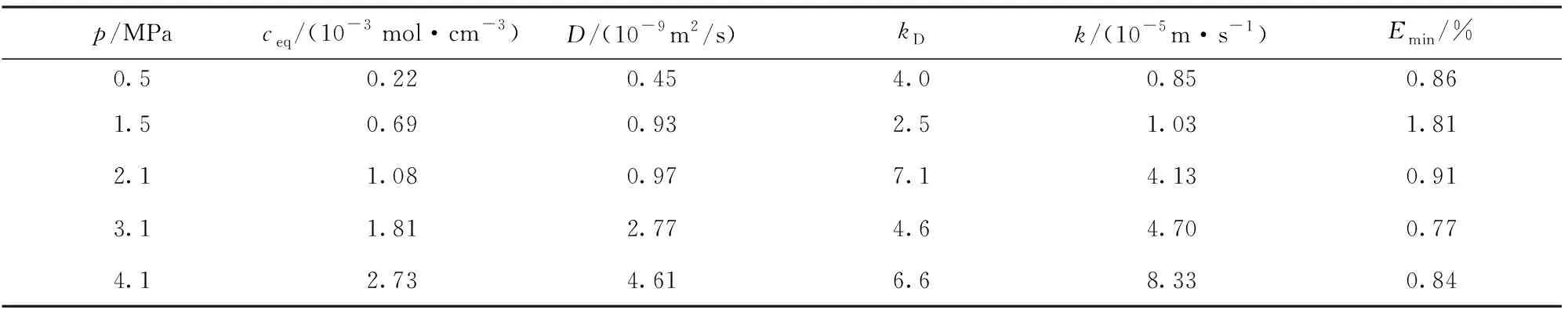
表2 300.15 K，不同压力下的CO2在原油中的平衡浓度、扩散系数D、传质Biot数kD、界面传质系数k以及全局最小目标函数Emin(%)

从表2还可以看出,CO2在原油中的平衡浓度随压力的升高而增大，CO2在原油中的溶解能够降低原油-CO2之间的界面张力，因为这样CO2能够更容易通过原油-CO2界面扩散进入原油相，造成高压下有更大的扩散系数和界面传质系数，这样，CO2-原油的动态界面张力在更短的时间内达到平衡界面张力。

4 结论

本文采用动态界面张力法研究300.15 K，0.5～4.1 MPa下CO2在中原油田胡12块轻质原油中的扩散系数和界面传质系数，得到原油-CO2体系的扩散系数为(0.45～4.61)×10-9m2/s，传质Biot数为2.5～7.1，界面传质系数为(0.85～8.33)×10-5m/s，模型计算与实验测得动态界面张力的均方根相对误差低于1.81%，说明本文建立的传质模型具有较好的稳定性，动态界面张力法在一定程度上能够用于CO2在原油中扩散系数的测定。