导数综合题中构造函数的两个着眼点

纵观近年各地高考试题，导数综合题的热度始终不减，也是试卷中难度较大，区分度较高的试题之一。而利用导数研究一个函数时，往往会涉及到构造新的函数，利用对新的函数的研究，来达到对原来函数研究的目的，在这个过程中，如何构造一个或多个恰当的函数，往往是学生觉得比较困难的地方。本文结合笔者的教学实践，谈谈构造函数的两个着眼点——形式优美、性质明晰。

一、构造形式优美的函数

形式服务于内容，形式上的美，必然意味着内容上的明确、深刻。因此，在构造函数时，要着眼于形式优美，构造出利于问题研究的恰当的函数。

1.构造结构协调的函数

结构协调是一种美，结构美的函数更有利于我们去研究，在实际应用中，要根据所研究的问题，着眼于函数的类型、次数、系数等，根据要解决的问题，构造结构协调的函数。

案例1（2018年高考全国卷III理科第21题）已知函数 f(x)=（2+x+ax2）ln（1+x）-2x.

（I）若 a=0，证明：当 -1＜x＜0 时， f(x)＜0；当x＞0时， f(x)＞0；

（II）若 x=0是 f(x)的极大值点，求 a.

分析对于第（I）小问，当a=0时，f(x)是一个不含参数的函数，于是利用导数研究函数的单调性，从而得到解答即可。

当 -1＜x＜0 时，g′(x)＜0；当 x＞0 时，g′(x)＞0.

故当 x=-1时，g(x)≥g(0)=0，且仅当x=0时，g(x)=0，从而 f′(x)≥0，且仅当 x=0 时，f′(x)=0，所以f(x)在（-1，∞）单调递增。

又 f(0)=0，故当 -1＜x＜0 时，f(x)＜0；当 x＞0时， f(x)＞0.

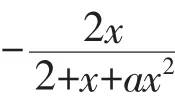
解：（II）①若 a≥0，由（I）知，当 x＞0 时，f(x)≥（2+x）ln（1+x）-2x＞0 = f(0)，这与 x=0 是 f(x)的极大值点矛盾。

又h(0)=f(0)=0，故x=0是f(x)的极大值点当且仅当x=0是h(x)的极大值点。

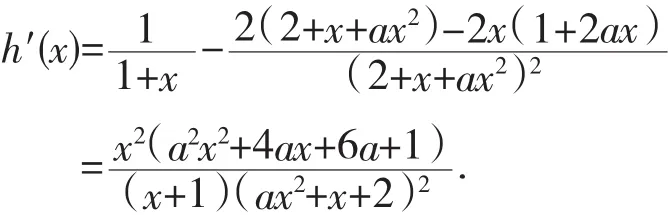
上述解法通过构造结构协调的函数，将一个复杂的函数转化为一个简单的函数，使得导数作为工具能更好地发挥作用，避免了多次求导带来的繁琐。

2.构造形式简洁的函数

（I）讨论f(x)的单调性；

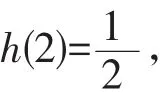
将一个形式复杂的函数转化为两个形式简洁的函数来研究，在问题解决的同时，也欣赏到数学的简洁之美，在理性思考中提升感性认识。

二、构造性质明晰的函数

彭海燕在《“套路”和“模型”视角下恒不等式问题的探讨》一文中曾谈到，在“套路”和“模型”视角下，根据常见函数如x与ex的和、差、积、商，x与lnx的和、差、积、商等“模型”，构造出凹凸性不一致的两个函数，从而很方便地对原问题进行研究，就是所谓的“套路”。实际上，构造的函数性质明晰，将有利于对其以及对原来函数的研究，这里谈的性质包括单调性、奇偶性、周期性、对称性、凹凸性，渐近线等。

案例3（2018高考天津卷理科第20题）已知函数 f(x)=ax，g(x)=logax，其中 a＞1.

（I）求函数h(x)= f(x)-xlna的单调区间；

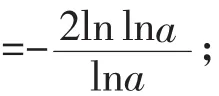
分析（I）（II）略.对于（III）曲线 y= f(x)在点（x1，ax1）处的切线 l1：y-ax1=ax1lna·（x-x1）.

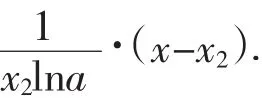
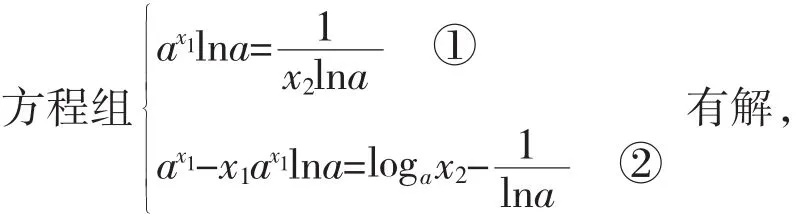
为此需要构造新的函数，站在函数的高度来研究方程解的情况。我们给出两种构造方法。

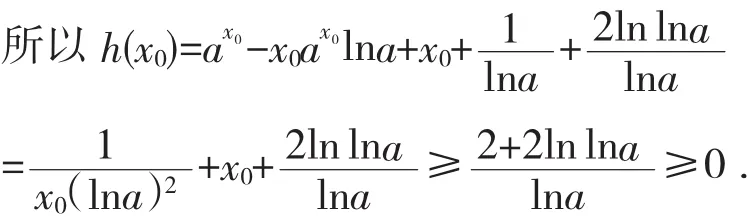
下面证明存在实数t，使得h(t)＜0.

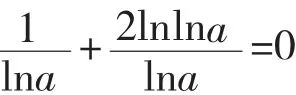
由上图可以很清楚地知道u(x)，v(x)的性质：当x→-∞ 时，u(x)→-1 且 u(x)＞-1，v(x)→0 且 v(x)＜0；

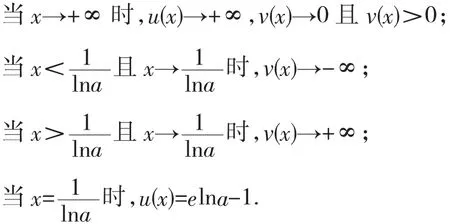
结合图像和性质可以得到解法二。

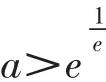
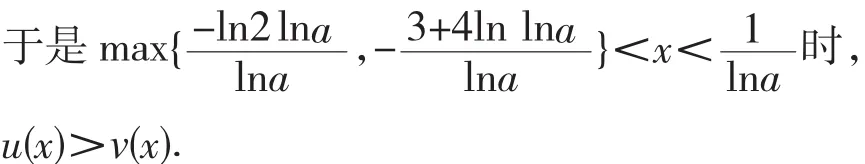
一般说来，形式优美是为性质明晰服务的，构造的函数结构协调、形式简洁，其性质也更容易凸显，更有利于我们对函数的研究与把握.因此，在实际教学中，引导学生关注形式、注重内容（性质），是一个重要的任务。