地铁隧道考虑流固耦合影响的微裂隙岩体注浆数值模拟研究
2018-11-01倪向阳李伟平
倪向阳, 徐 程, 李伟平
(1. 青岛地铁集团有限公司, 山东 青岛 266000; 2. 山东大学岩土与结构工程研究中心, 山东 济南 250061)
0 引言
地铁隧道施工过程中经常穿越微风化岩石地层,微风化岩石地层中一般发育开度较小(0.1~0.3 mm)的微裂隙。在地下水丰富的地区,微裂隙作为导水通道会沟通地下水与隧道临空面,造成隧道渗漏水。目前,注浆是治理微裂隙岩体渗漏水的最常用手段。
裂隙岩体注浆过程是裂隙岩体变形与浆液扩散过程的耦合过程,尤其在微裂隙岩体注浆工程中,注浆压力相比正常裂隙岩体注浆压力更高,流固耦合效应更为显著。浆液在注浆压力的作用下进入岩体微裂隙中,浆液压力作为外荷载作用于裂隙岩体,裂隙两侧岩体发生变形,进而影响整个岩体的受力变形状态,裂隙开度逐渐增大。逐渐增大的裂隙开度会导致裂隙渗透性能发生改变,进而影响浆液流场。
关于裂隙注浆理论,国内外学者进行了广泛的研究。文献[1]建立了基于浆液黏度时变性的岩体裂隙注浆扩散模型; 文献[2-5]推导了C-S浆液在单一平板裂隙中的压力分布方程; 文献[6-12]提出了相对扩散距离与相对扩散时间的概念,并用于描述裂隙注浆过程; 文献[13]研究了浆液压力与裂隙变形之间的关系,引入了裂隙张开临界压力的概念; 文献[14]研究了裂隙岩体注浆过程中裂隙张开变形机制,并讨论了裂隙张开变形对注浆效果的影响; 文献[15]通过有限元方法获得了相应的裂隙开度变化规律。以上研究均侧重于裂隙内部的浆液流动过程,并假定裂隙开度在注浆过程中保持不变,与实际情况存在明显差异。
本文着重考虑微裂隙岩体注浆过程中的流固耦合效应,进行有限元建模及计算分析,获得考虑流固耦合效应的微裂隙岩体注浆扩散过程计算方法,研究裂隙开度及岩体弹性模量对注浆扩散过程的影响。对于微风化地层隧道中出现的渗漏水问题,基于本文所提出的计算方法能够计算浆液的扩散距离以及围岩的变形量,为实现渗漏水安全有效的控制提供了新的思路。
1 流固耦合理论
1.1 基本假设
1)岩体微裂隙简化为平板裂隙,实际裂隙内部为不平整接触面,裂隙粗糙度对渗透性能的影响转化为裂隙渗透率对浆液扩散过程的影响。
2)裂隙两侧岩体视为各向同性、均质的完全弹性体,裂隙上下表面满足无滑移边界条件,裂隙表面处浆液流动速度为0。
3)浆液和水均为均质、各向同性的流体,浆液为牛顿流体,且注浆过程中浆液流型不变。
4)浆液扩散方式为完全驱替扩散,不考虑浆水相界面处水对浆液的稀释作用。
5)不考虑浆液渗透到裂隙两侧岩体,浆液只在裂隙中扩散。
1.2 控制方程
地下水在隧道围岩中的渗流运动通过达西定律描述,岩土体的应力与变形通过经典弹性力学理论描述。根据有效应力原理,水压力与岩土体骨架有效应力之和为岩土体总应力。
浆液在裂隙内部的流动采用裂隙流理论描述,控制方程如下。
渗流连续性方程为:
。
(1)
裂隙流动立方达西定律运动方程为:
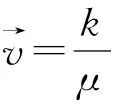
。
(2)
考虑流体的压缩性,流体状态方程为:
ρ=βρ0e-βp
。
(3)
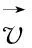
根据弹性力学理论,岩土体受力变形服从平衡方程、几何协调方程及本构方程。
岩体力学平衡方程为:
σji,j+Fi=0
。
(4)
几何协调方程为:
本构方程为:
式(4)—(7)中:σ为岩土体应力,Pa;F为岩土体附加应力,Pa;ε为岩土体应变;E为弹性模量,Pa;u为岩体位移,m;δ为克罗内克符号;υ为泊松比。
浆液流动过程中通过裂隙表面向岩体传递浆液压力,在裂隙表面处,浆液压力与岩体应力相等,浆液流动与围岩变形之间相互影响的理论纽带即为裂隙表面处的压力相等条件,如式(8)所示。
p界面,围岩=p界面,流体
。
(8)
式中:p界面,围岩为界面处围岩应力;p界面,流体为界面处流体压力。
2 有限元数值模型创建
采用Comsol Multiphysics创建数值模型,该软件是以有限元法为基础,通过求解偏微分方程(单场)或偏微分方程组(多场)来实现多物理场仿真计算。计算模型由裂隙与围岩体构成,如图1所示。裂隙采用单一水平裂隙,裂隙上下为围岩体。
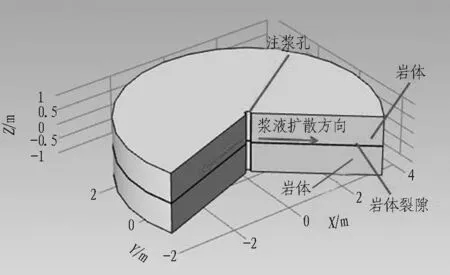
图1 裂隙注浆计算模型
计算模型依托青岛地铁2号线东—环区间花岗岩微裂隙注浆堵水工程,根据现场对微裂隙花岗岩的裂隙统计,花岗岩裂隙开度为0.1~0.3 mm。本文裂隙开度计算参数取0.1 mm及0.3 mm 2种工况,通过钻孔取芯测得花岗岩弹性模量为30~50 GPa。为研究不同围岩弹性模量条件下流固耦合效应对注浆扩散过程的影响,花岗岩弹性模量取30 GPa和50 GPa 2种工况,花岗岩泊松比取0.3。注浆材料选用mw/mc=1∶1水泥单液浆,该种浆液黏度为10 MPa·s,注浆孔半径取0.02 m,注浆流量取3 L/min。模型计算参数如表1所示。
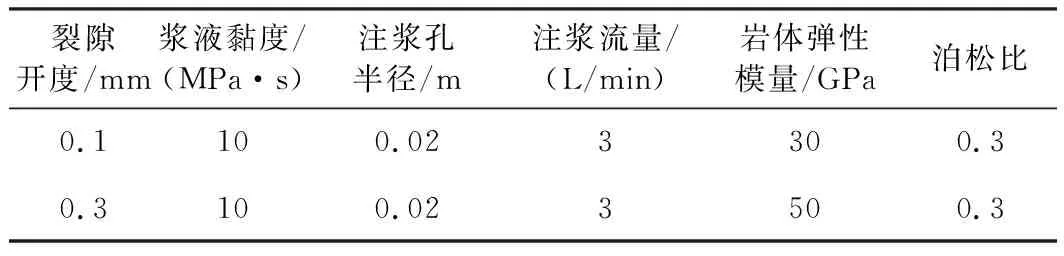
表1 模型计算参数
模型网格剖分及边界条件如图2所示。计算模型由3部分构成,模型中间为裂隙,裂隙上下均为岩体,裂隙单侧岩体厚度为1 m,半径为4 m。模型上下边界均为固定边界,不发生任何移动。模型侧边界为辊支撑边界,只能发生竖直方向的位移,不能发生水平滑动。裂隙边界为自由变形边界,在浆液压力作用下会发生被动变形,浆液由注浆孔位置进入裂隙。模型网格采用细化自由4面体网格,最小单元尺寸为0.02 cm,最大单元尺寸为4 cm,曲率解析度为0.25。为提高计算精度,在裂隙附近采用加密网格。
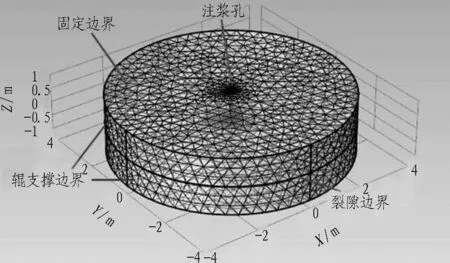
图2 模型网格剖分及边界条件
为研究注浆扩散动态过程,采用流体力学模块与固体力学模块进行多物理场瞬态计算。
3 微裂隙岩体注浆扩散规律分析
从浆液扩散压力场、围岩受力变形、裂隙开度时空分布、注浆压力与注浆时间以及浆液扩散半径的关系等方面对注浆扩散过程进行分析研究。
3.1 压力场时空分布规律
注浆过程中压力场时空分布对比如图3所示。
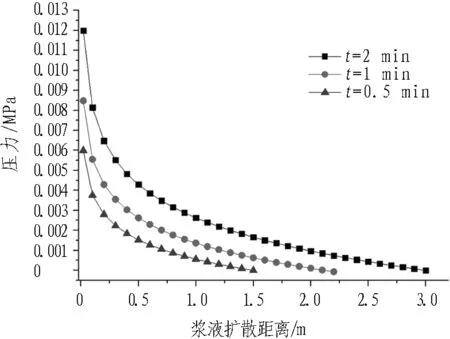
(a) E=30 GPa, b=0.3 mm
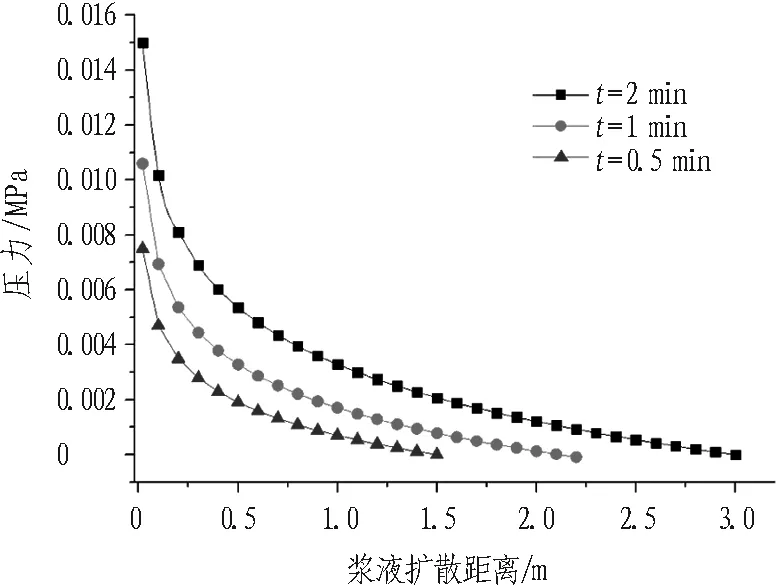
(b) E=50 GPa, b=0.3 mm
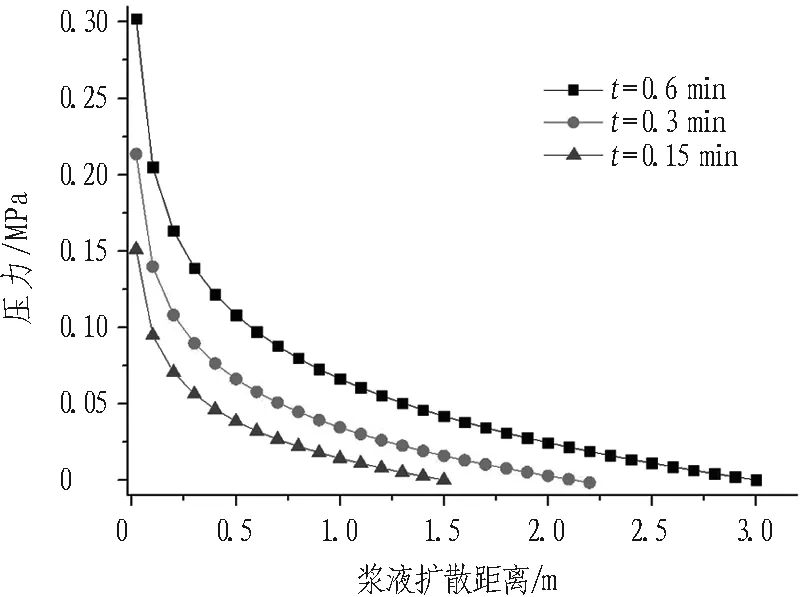
(c) E=30 GPa, b=0.1 mm
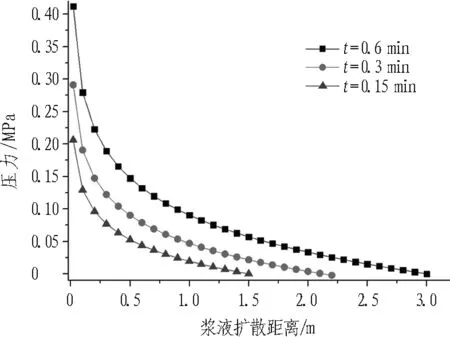
(d) E=50 GPa, b=0.1 mm
Fig. 3 Relationships between stress filed and grouting diffusion distance
由图3可知:
1)同一时刻,浆液压力沿扩散方向衰减,衰减速率随扩散距离减小。
2)同一位置处,浆液压力随时间推移而升高。由于浆液扩散范围的增加,进一步扩散所受到的阻力增大。
3)相同岩体弹性模量,裂隙开度越大,同一时刻、同一位置处,浆液压力越小,浆液扩散距离越大。
4)相同裂隙开度,岩体弹性模量越小,浆液压力越小。推断是由于弹性模量越小,相同浆液压力作用下,裂隙开度增加越大,浆液耦合效应越明显的原因。
3.2 围岩受力变形规律
E=30 GPa、b=0.1 mm时围岩受力云图如图4所示。
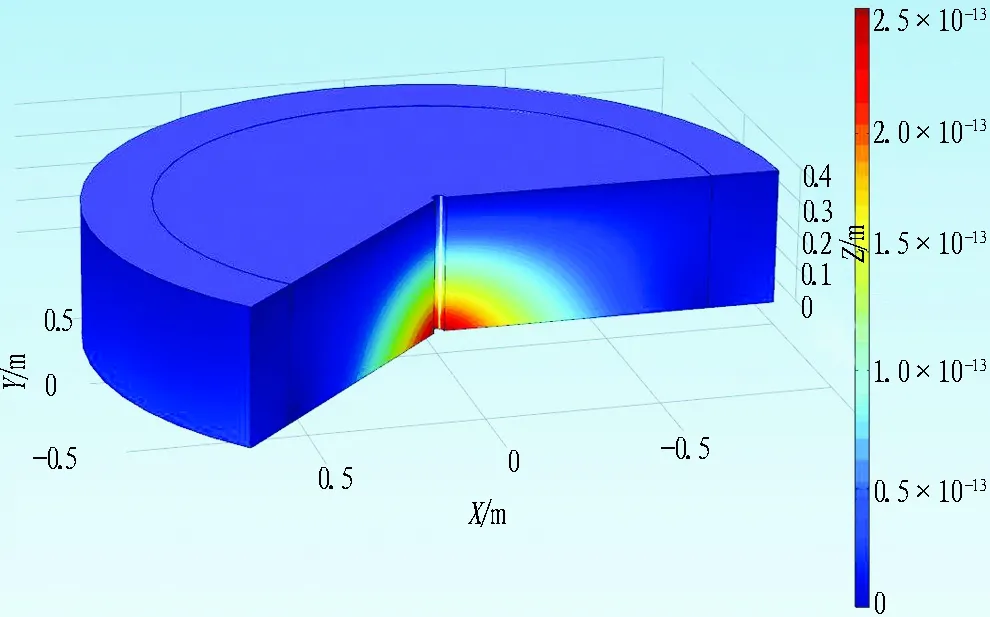
图4 围岩受力云图(单位: GPa)
由图4可知:
1)由于浆液压力沿扩散半径衰减,相应的作用于围岩体的压力也沿着扩散半径衰减,注浆孔附近围岩应力相对集中; 随着浆液扩散距离的增大,围岩所受应力逐渐减小。
2)由于注浆孔附近应力较为集中,当注浆压力超过围岩可承受的安全注浆压力时,注浆孔附近区域最先发生塑性破坏。
3.3 裂隙开度时空变化规律
不同工况条件下,裂隙开度时空变化如图5所示。
由图5可知:
1)裂隙开度由注浆孔附近向浆液扩散锋面处衰减,这与浆液压力的空间衰减相对应,注浆孔附近的浆液压力较高,对应的裂隙开度变化量大,最终获得的裂隙开度也较大。
2)裂隙开度空间衰减速率随着距注浆孔距离的增大而增大,这与注浆孔附近应力的快速衰减相对应。
3)不同弹性模量对应的裂隙开度稍有差别,当岩体弹性模量较大时,岩体不容易发生变形,导致浆液扩散阻力增加,同一位置处的浆液压力随之增大,但是由于岩体变形量较小,浆液压力增大所应该引起的裂隙开度增加被岩体弹性模量增加所带来的变形减小相互抵消,最终导致不同弹性模量岩体所对应的裂隙开度有差别,但差别不大。
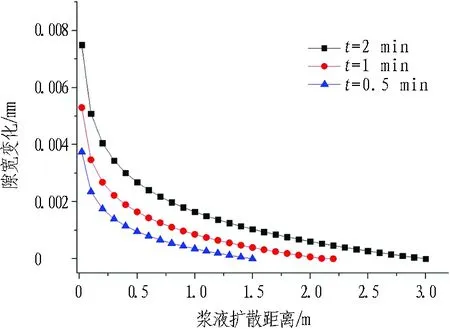
(a) E=30 GPa, b=0.3 mm
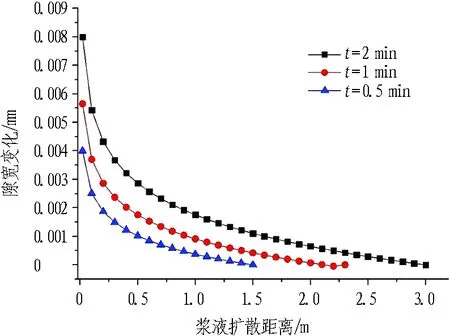
(b) E=50 GPa, b=0.3 mm
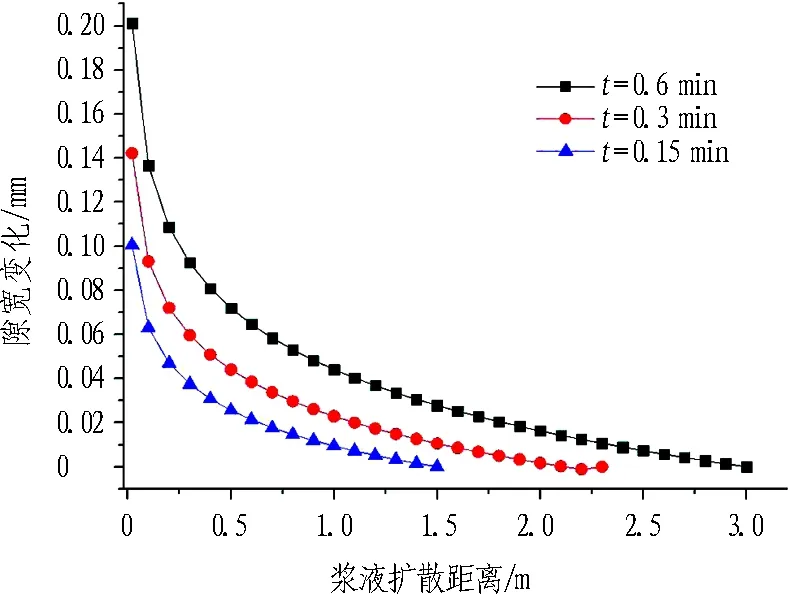
(c) E=30 GPa, b=0.1 mm
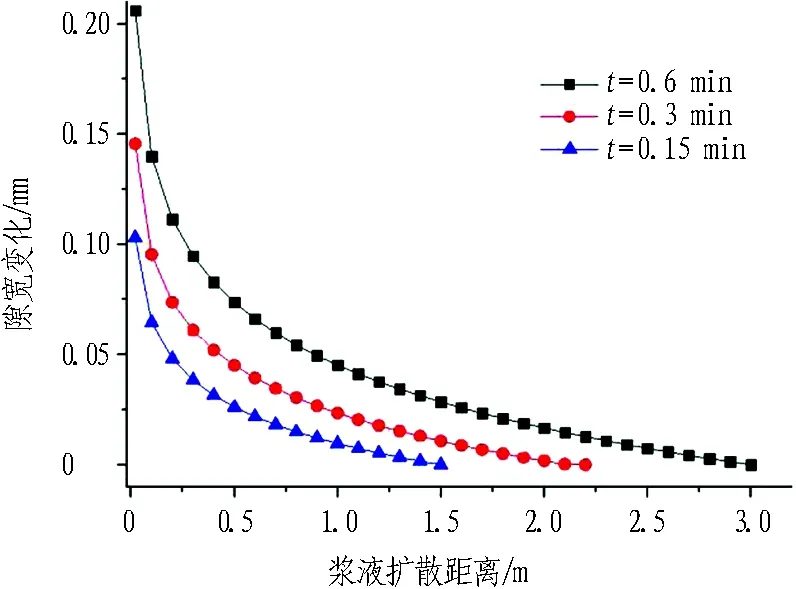
(d) E=50 GPa, b=0.1 mm
Fig. 5 Relationships between fracture opening and grouting diffusion distance
3.4 注浆压力增长规律
不同工况条件下,注浆压力随时间变化规律如图6所示。
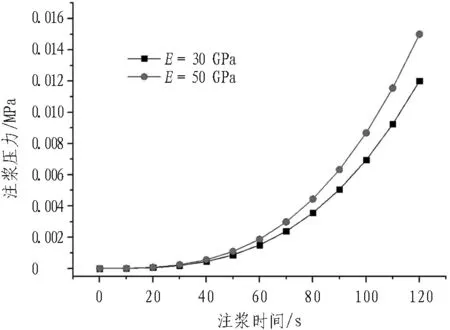
(a) b=0.3 mm
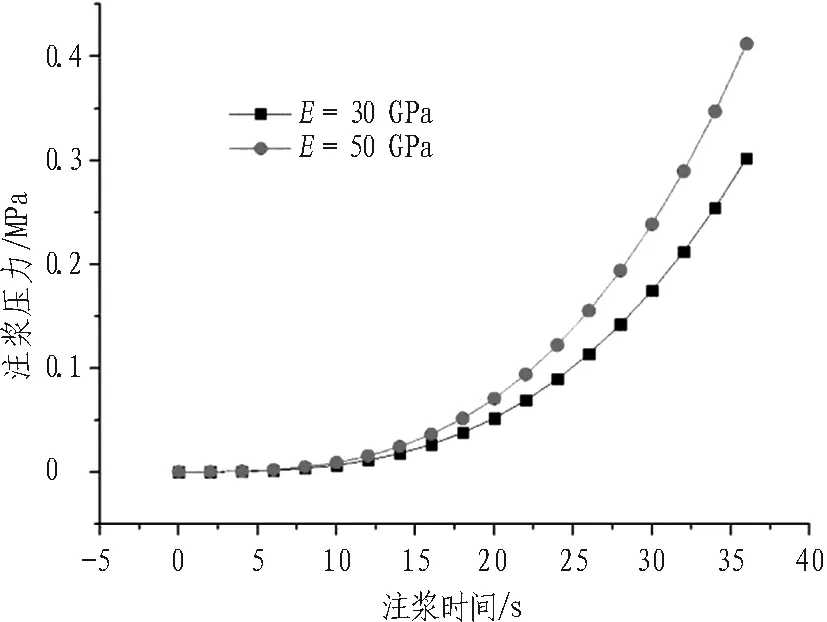
(b) b=0.1 mm
由图6可知:
1)随着注浆时间的增加,注浆压力相应增大,注浆前期注浆压力增长速率较慢,注浆后期注浆压力增长速率加快。
2)当裂隙两侧围岩弹性模量较大时,注浆压力相应较高,这是因为围岩弹性模量较高时围岩难以压缩变形,裂隙开度变化不大,故在该条件下对浆液扩散的阻力较大,最终导致注浆压力较高。
4 考虑流固耦合效应的必要性分析
由于流固耦合效应的影响,岩体裂隙由于承受浆液压力而导致裂隙隙宽变大,裂隙渗透率增大,进而导致裂隙岩体本身所引起的浆液扩散阻力减小。以往裂隙岩体注浆扩散理论较少考虑流固耦合效应对注浆扩散过程的影响,导致注浆压力、注浆扩散范围与实际测量值有较大区别,本节通过考虑与不考虑流固耦合效应时注浆压力与浆液扩散范围的对比,分析考虑流固耦合效应的必要性。
4.1 注浆压力方面
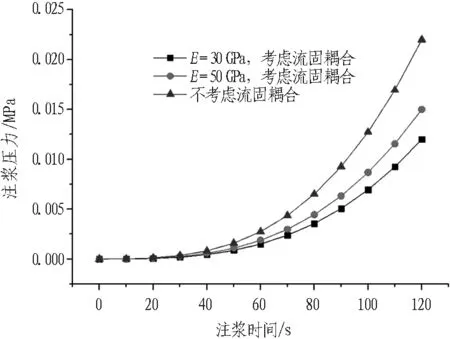
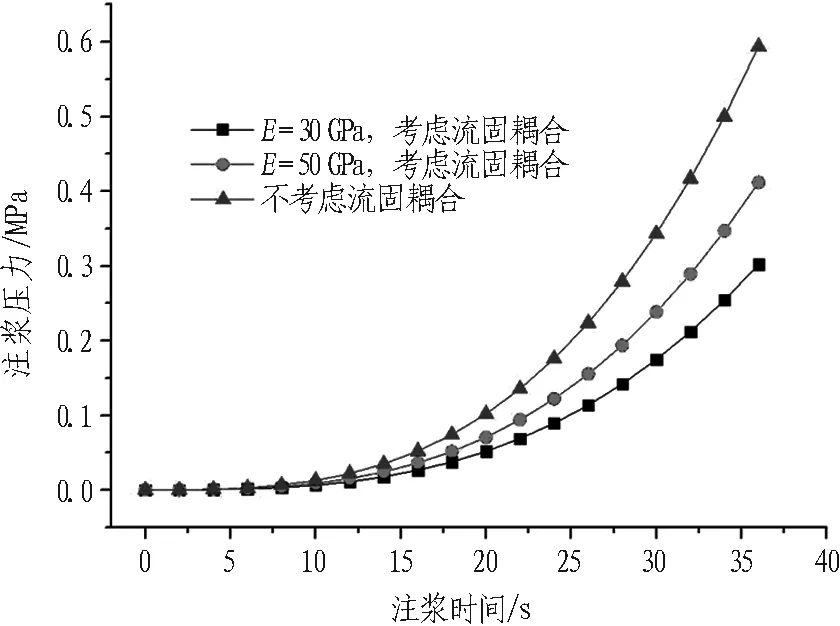
考虑与不考虑流固耦合效应2种情况下注浆压力对比如图7所示。
(a) b=0.3 mm
(b) b=0.1 mm
Fig. 7 Grouting pressures with and without consideration of fluid-solid coupling
不考虑流固耦合效应时,由于裂隙开度维持不变,浆液扩散阻力相比实际情况偏大,达到相同浆液扩散半径时对应的注浆压力也相应偏大。当裂隙开度较小时,考虑与不考虑流固耦合效应所引起的注浆压力数值差别更大,不考虑流固耦合效应时注浆压力的计算误差可达到30%以上。
4.2 浆液扩散半径方面
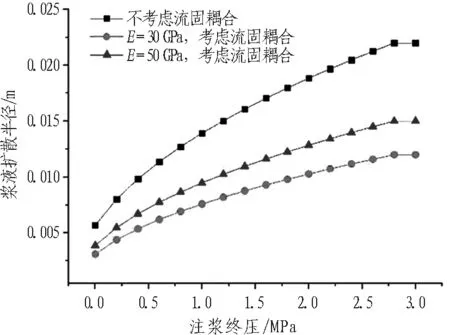
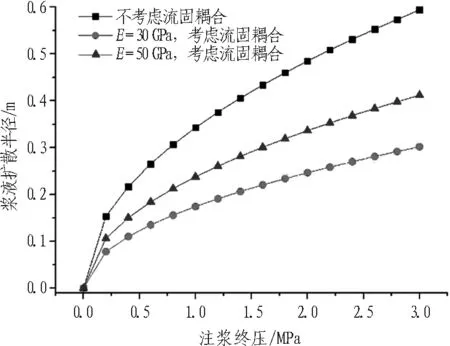
相同注浆压力条件下,考虑与不考虑流固耦合效应所得浆液扩散半径的大小对比如图8所示。
不考虑流固耦合效应时,浆液扩散阻力相比实际情况偏大,相同注浆终压条件所对应的浆液扩散半径偏小。当裂隙开度较小、岩体弹性模量较小时,考虑与不考虑流固耦合效应所引起的注浆压力数值差别更大,不考虑流固耦合效应时注浆扩散半径的计算误差可达到15%以上。
通过以上分析可知,不考虑流固耦合效应计算得到的注浆压力明显偏高,浆液扩散半径明显偏低,故在注浆设计中应充分考虑流固耦合效应对注浆扩散过程的影响。
(a) b=0.3 mm
(b) b=0.1 mm
Fig. 8 Grout diffusion radius with and without consideration of fluid-solid coupling
5 结论与讨论
1)综合考虑浆液流场与围岩变形之间的耦合作用,建立了考虑流固耦合效应的单一裂隙注浆扩散有限元计算模型,实现了注浆扩散过程的动态模拟。
2)注浆压力由注浆孔向浆液扩散锋面方向非线性衰减,导致注浆孔附近围岩应力相对集中,注浆孔附近区域最先发生塑性破坏。
3)裂隙开度由注浆孔附近向浆液扩散锋面处衰减,这与浆液压力的空间衰减相对应,注浆压力非线性增长。
4)在微裂隙岩体注浆中,不考虑流固耦合效应时注浆压力的计算误差可达到30%以上,注浆扩散半径的计算误差可达到15%以上,所以在注浆设计中应充分考虑流固耦合效应对注浆扩散过程的影响。
5)由于岩体裂隙发育情况复杂,很难通过单一的裂隙注浆计算结果来表征整个岩体裂隙网络的注浆扩散情况,这方面还有待于开展进一步的研究。
