大瑞铁路高黎贡山隧道原岩温度预测

2018-11-01李宜轩王树刚罗占夫

隧道建设(中英文) 2018年10期

尹龙, 李宜轩, 王树刚,*, 蒋爽, 罗占夫, 王卓

(1. 中铁隧道局集团有限公司勘察设计研究院，广东广州 511458； 2. 大连理工大学, 辽宁大连 116024；3. 大连民族大学，辽宁大连 116600)

0 引言

随着交通运输的迅速发展及隧道施工技术的不断提升，铁路、公路等隧道建设规模越来越大。由于长隧道可以克服地形障碍，近年来深埋长隧道的数量得到快速增长。相比以往的铁路、公路隧道，深埋隧道的热害问题突出，作业环境恶化，严重影响施工人员的工作效率，而且由于产生的附加温度应力还可能引起衬砌开裂，破坏隧道的稳定性[1]，故需要根据地温的分布特征来对隧道高温地段采取必要的降温措施。本文研究的隧道地温场位于大瑞铁路高黎贡山越岭地段。大瑞铁路位于云南省西部，起于大理市，终于瑞丽市，线路在穿越高黎贡山时，以隧道形式通过。

一般来说，隧道周围的原岩温度随埋深的增加而升高，特别是隧道上方的原岩温度。隧道原岩温度场的预测可以采用数值模拟和解析方法，并应用现场监测结果修正有关参数。陈永萍等[2]针对秦岭隧道可能存在的热害问题，分析钻孔实测温度等相关资料，建立了秦岭隧道岩温预测经验公式，并对秦岭隧道岩温进行预测。杨平平[3]根据吉沃希嘎隧道钻孔的实测温度，运用加权平均值对数据进行回归公式计算，得到相应的地温计算公式及高地温区地温梯度。文献[2-3]的研究针对地域性强，没有广泛的适用性。

陈尚桥等[4]运用导热方程建立数学模型，并依据地质及地温实测资料，在已知少量地温数据作为拟合点的条件下，运用有限元反演法对水电站引水隧洞温度场进行较准确的数值模拟研究。邵珠山等[5]通过建立两端简支的二维稳态热传导方程和平衡方程，导出了圆形断面隧道边界和围岩的温度场、位移场及应力场的解析解，在假设围岩温度已知的情况下，分析了隧道开挖造成的围岩温度变化的影响范围。实际上在1950年，F.Birch[6]基于地质演化历史的几种不同假设提出了对地形的修正方法，获得了2种地温梯度修正值，分别对应于2个假设：一是现有地形保持不变；二是地貌特征来源于百万年以来古老地表面的抬升和侵蚀。由此获得了山体地表下某一埋深处的原岩温度数学表达式，主要用于地热流的计算，但没有在隧道原岩温度计算中得到广泛应用。1979年和1994年，P.Bodmer等[7]和L.Rybach等[8]将F.Birch[6]方法中三维地形对某一点原岩温度的影响简化为温度修正值，代入一个由地表面温度和局部地温梯度计算原岩温度的表达式，并编写计算程序预测隧道地温场，将其应用于Gotthard公路隧道中进行地温场测算，在受地下水影响较弱的隧道施工地段，计算值同温度实测值吻合较好;但是未分析温度修正值的简化表达式对预测结果的影响。

本文基于F.Birch[6]提出的地质演化历史方法，应用相应的地温场计算模型(将P.Bodmer等[7]和L.Rybach等[8]的温度修正表达式复原为F.Birch[6]提出的原始表达式)，特别是引入“谷地地理信息系统”获取较为准确的地形数据，对高黎贡山隧道进行原岩温度预测，并对隧址区的温度场进行简单划分。

1 数学模型的描述

假定山体初始地表面和隧道横断面如图1所示。经过地质演化(定义时间为t)后，抬升高度为L。隧道所处位置位于初始地表面下的距离为D，经过抬升后距离不变。P5为计划开挖隧道中某个位置点，其对应的地表点为P2。

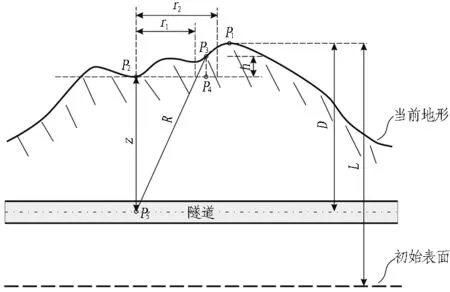
图1 隧道横断面示意图

一般情况下原岩温度随深度增加而升高，但是复杂的地形表面也会对地下埋深至数千米的岩温产生影响。其他的影响因素还包括地表温度、当地热流密度及各种地质参数(如地质构造、热导率、侵蚀率等)，其中地质参数影响导热系数分布。在隧道未开挖条件下，基于固体热传导理论，在考虑地质演化历史(包括抬升和侵蚀过程)的情况下，得到图1中P5点温度的简化计算式，如式(1)所示[6]。

(1)

为简化计算过程，以P2为圆心，将经过P2的平面划分为若干个圆环，式中hr为每个圆环内地形的平均海拔高度与P2点海拔高度的差值。Er的计算如式(3)所示。

Er=E(β)=2erfc(β)-4i2erfc(β)。

(3)

其中：

ΔΩr/(2π)为圆环(内外半径分别为r1和r2)与P5点的立体弧度，计算如式(6)所示。

重复上述过程，计算出隧道方向每间隔一定距离(如1 km)的原岩温度。将计算结果与实测数据进行对比，可对α的取值进行修正。

对上述计算模型编制计算程序，根据每个采样点的坐标位置更新所划分圆环的数据，计算地形修正值，进而获得预测的温度值。

2 隧道山体概况和地形数据获取

2.1 隧道山体概况

高黎贡山隧道位于怒江车站与龙陵车站之间，隧道进口里程为D1K192+302，出口里程为D1K226+840，隧道全长34 538 m。研究区域属热带—亚热带季风气候区，日照丰富，雨量充沛，气温年差小，日差大，年平均气温为14.9～19.5 ℃。受孟加拉湾暖温气流控制，研究区每年5—10月为雨季，11月—次年4月为旱季，年平均降雨量为967.1～2 105.7 mm，最大可达 2 597.7 mm。受地形条件的影响，降雨量有随地形增高而增加的规律。

2.2 地形数据获取

基于“谷地地理信息系统”，获取计算点周围约35 km的地形数据，对施工图中地形数据进行扩充。将所获取的地形数据与施工图中若干位置的海拔高度进行对比，误差在可接受的范围之内。北京54坐标系下计算区域地形如图2所示。

图2 北京54坐标系下计算区域地形

Fig. 2 Calculation of regional topography in Beijing 54 coordinate system

2.3 计算参数取值

式(1)计算用到的几个参数中，D近似取隧道在整个山体中的最大埋深，即1 200 m；L为山体抬升高度，近似取2 000 m；地表面温度梯度α′根据实测数据拟合得到，为0.005 ℃/m；温度扩散系数k，根据岩性参数近似取为0.02×10-4m2/s，经过敏感性分析发现k取值对计算结果影响较小；初始岩温梯度α对结果影响较大，其取值根据实测数据，经过反算获取，针对该隧道项目取值为0.013 5 ℃/m。此外，在地形修正值的计算中，距离计算点地面水平距离越近的地形对计算点温度影响越大，故距离越近的圆环划分越细，本文计算时，对于第i个圆环的内外半径分别取为30×1.5i-1m和30×1.5im。

3 温度预测

3.1 钻孔温度计算

将北京54坐标系下的钻孔点平面坐标和相应埋深输入计算程序中，计算相应的温度，与实测温度数据进行对比，从而对模型进行验证。实测地温数据选取文献[9]中公布的若干钻孔温度数据以及项目施工图中的地质勘测数据。北京54坐标系下计算区域钻孔点坐标如表1所示。钻孔温度计算值与实测值对比分别如表2和图3所示。从温度值对比来看： 1)大部分计算值与实测值的变化趋势一致，表明所建立的数学模型和计算程序是可靠的；2)个别钻孔的计算值与实测值误差较大，主要受地下水流的影响。当钻孔内有以下渗为主的地下水垂向运动时，钻孔内原始地温将受地下渗水流的影响而降低；当钻孔位置有地下热水向上排泄的通道时，钻孔位置附近原始地温将会升高。程序计算时，参数取统一的数值，尤其是初始岩温梯度α对结果影响较大，但并未针对局部特殊的地质特征进行修正。在隧道建设过程中，当发现实际地温与预测值偏差较大时，应特别注意地下断层及水流情况[10-11]。

3.2 隧道温度计算

将从“谷地地理信息系统”中获取的地形数据及相应的关键参数作为数据基础。将隧道进口里程D1K192+302处取为计算起点，沿隧道约770 m取为第2点，此后以1 km为采样间距，沿隧道取33个采样点，第35采样点距第36采样点(计算终点)约768 m。将采样点在北京54坐标系下的平面坐标及相应埋深输入计算程序中，计算得到沿隧道方向未开挖情况下的地温数据(不考虑断裂带的影响)。沿隧道方向岩石温度曲线如图4所示。可以看出： 1)在距隧道起点约8 770 m处，隧道原岩温度达到最高，约 31.7 ℃； 2)沿隧道向瑞丽方向，岩温呈现出先增大后减小的规律。

表1 北京54坐标系下计算区域钻孔点坐标

表2钻孔计算温度与实测温度对比

Table 2 Comparison between calculated temperature and measured temperature of boreholes℃

图3 钻孔温度计算值与实测值对比

Fig. 3 Comparison between calculated temperature and measured temperature of boreholes

图4 隧道岩温预测

3.3 山体温度计算

依据文献[12]中介绍的高地温分级和规范[13]：“隧道内气温不得高于28 ℃”，当气温超过28 ℃时，高地温引起的热害问题开始严重，需要采取降温措施。山体温度场分布如图5所示。可沿隧道洞线方向进行温度划分：沿隧道瑞丽方向，隧道开始大约2.5 km以内及18 km至隧道终点段，隧道岩温为28 ℃以下；2.5～18 km段隧道岩温为28～31.73 ℃，需要进行实时温度监控，采取必要的降温措施，例如加强隧道内通风、采用冰制冷系统及建立制冷站作冷源等[14-15]。综上可知，需根据隧道所处环境及施工条件选择最有效的解决方案。