基于谱聚类的全局中心快速更新聚类算法
2018-11-01邹臣嵩
邹臣嵩,刘 松
(1.广东松山职业技术学院电气工程系,广东 韶关 512126; 2.广东松山职业技术学院机械工程系,广东 韶关 512126)
0 引 言
聚类分析作为一种探索性分析方法被广泛应用于模式识别、计算机视觉、数据挖掘等领域中,其目的是根据相似性原则将物理或抽象的对象集合分成若干个子集,并分析各子集中的数据之间的内在联系、规律和特点[1]。K-means聚类算法是应用最为广泛的划分方法之一,其实现简单、快速,并且能有效地处理大数据集,但该算法对初始聚类中心和异常数据较为敏感,且不能用于发现非凸形状的簇,因此聚类结果不稳定[2-3]。为了解决K-means算法的这些问题,研究人员围绕簇中心的选择与优化提出了新的计算方法[4-10],提高了原算法的聚类质量,减少了聚类时间,但这些改进的聚类算法更多注重初始聚类中心的选择,针对的对象往往是低维数据,因此,当数据的维度升高、分布相对稀疏时,其聚类结果难以预料,这是因为在高维空间中,数据对象间的距离几乎一致,所以基于距离和密度的聚类算法在面对高维数据集时,整体性能有所下滑[11]。此外,随着数据特征维度的增加,不相关的特征值会产生大量的冗余信息,在一定程度上屏蔽了那些与真实聚类结果关系密切的特征信息,从而进一步地影响了算法的聚类结果。因此,聚类算法的改进不仅需要寻找合理的初始聚类中心,还要对原始数据进行有效的预处理,尤其对于高维数据,在对其降维的同时,应尽可能地挖掘并保留能够对聚类结果的划分产生重要影响的“核心特征”。
1 相关算法的研究现状
在聚类算法的改进方面,段桂芹[4]选取数据对象到样本均值和当前聚类中心集合的距离乘积最大值法来确定新的初始聚类中心,克服了聚类结果对初始聚类中心的依赖性。熊忠阳等[5]对最大最小距离法进行了改进,提出了最大距离乘积法,解决了原方法因选取初始聚类中心过于稠密而导致的聚类冲突等问题。翟东海等[6]提出了最大距离法选取初始簇中心的K-means文本聚类算法,解决了K-means算法的聚类结果不稳定、总迭代次数较多等问题。贺思云等[7]用改进的人工蜂群算法优化K-means算法的聚类中心,用最大距离乘积法对蜜源进行初始化,增加蜜源搜索范围的动态调整因子,加快了算法的收敛速度。周鹿扬等[8]提出了一种基于聚类中心的快速聚类算法,将数据集中较大或延伸状的簇分割成若干球状簇,而后合并这些小簇,较好地适应任意形状数据集。李晓瑜等[9]提出了一种基于Hadoop的分布式改进K-means算法,通过引入Canopy算法初始化聚类中心,克服K-means算法因初始中心点的不确定性,易陷入局部最优解的问题。同时,结合MapReduce分布式计算模型,给出改进后算法的并行化设计方法和策略。张顺龙等[10]提出了一种基于动态类中心调整和Elkan三角判定思想的加速K-means聚类算法,采取动态及时更新类中心策略,有效降低了算法的迭代次数和内存开销。
随着降维技术理论研究和实践应用的不断深入,许多降维算法在特定的领域也发挥着重要的作用。如Luebke和Weihs[12]提出了一种两步骤适应过程的线性数据降维算法,自适应地完成各种类型数据的降维分类处理,但处理较多异常数据集时性能不稳定。Magdalinos等[13]针对高维数据集提出了一种快速降维算法,主要思路是将数据对象间的距离嵌入到低维的投影空间,显著加快K-means的收敛速率。Ge等[14]提出了一种几何局部嵌入的降维方法,该方法用几何距离来测量数据内部相邻节点的距离以达到高维数据的清晰可视化,这种几何距离强调了由中心向量所生成的局部几何结构,而不用再计算数据的成对距离。Li等[15]提出了一种基于归一化网格子空间的高维数据相似性度量方法,将每个维度的数据区间划分为若干个区间,并将不同维度的组件映射到相应的区间上,仅使用相同或相邻区间中的组件来计算相似度。
受上述文献启发,本文以数据预处理技术中的降维为突破口,针对数据降维、初始聚类中心选择、簇中心更新等关键问题,提出了基于谱聚类的全局中心快速更新聚类算法。首先完成数据从高维到低维的转换,然后对文献[6]的最大距离法进行了改进,得到了更加分散、更具有代表性的初始聚类中心;在簇中心更新过程中,用均值最近点作为新的簇中心,取代了K-means算法的均值中心法。实验测试表明,本文算法的聚类准确率、整体耗时、rand指数等有效性评价指标优于传统K-means算法和其他3种改进算法。
2 基于谱聚类的全局中心快速更新聚类算法
本文算法分为3个阶段:数据预处理、选择初始聚类中心和更新簇中心,基本思路如下:
1)在数据预处理阶段,采用谱聚类算法[16]对样本进行降维,并对降维后的数据进行归一化处理。
2)在选择初始聚类中心阶段,首先计算样本集X中各数据对象之间的距离,构建整个样本集的距离矩阵;再在距离矩阵中选取k个首尾相连且距离乘积最大的数据对象作为初始聚类中心,得到初始聚类中心集合Z={Z1,Z2,…,Zk}。
3)在更新簇中心阶段,为缓解K-means算法对孤立点的敏感性,本文借鉴K-medoids算法的思想,选取与簇均值距离最近的数据对象作为簇中心,构建新的簇中心集合Z′={Z1′,Z2′,…,Zk′},再将样本集X中其他数据对象按最小距离划分到相应簇中,重复迭代过程,直至准则函数收敛,最终完成聚类。
下面是本文算法的相关概念、算法描述以及算法复杂度分析。
2.1 基本概念与定义
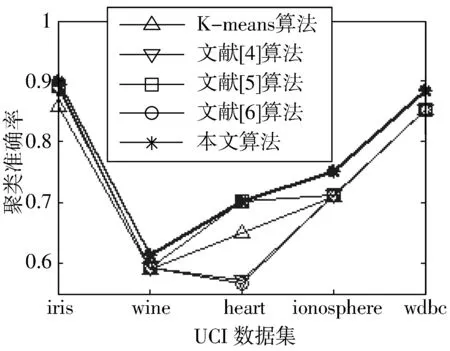
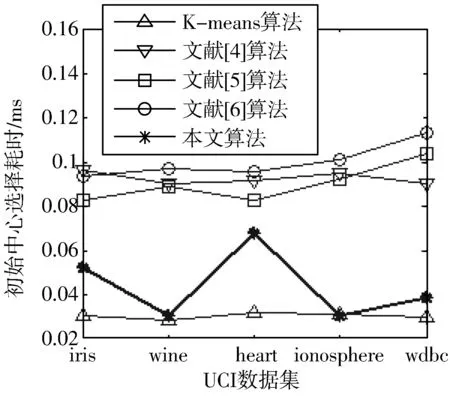
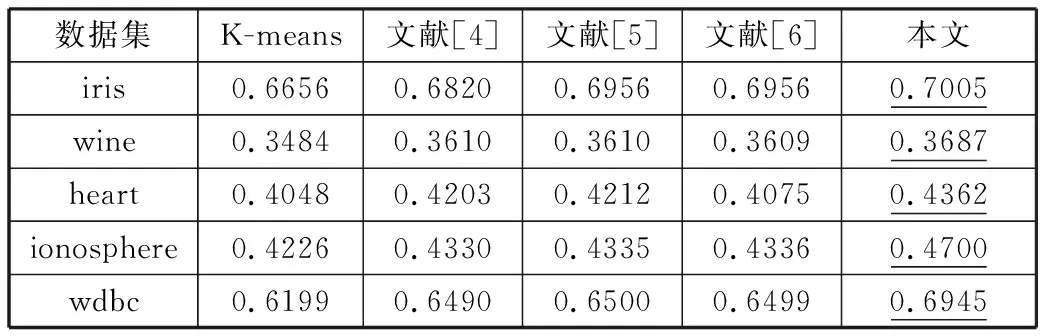
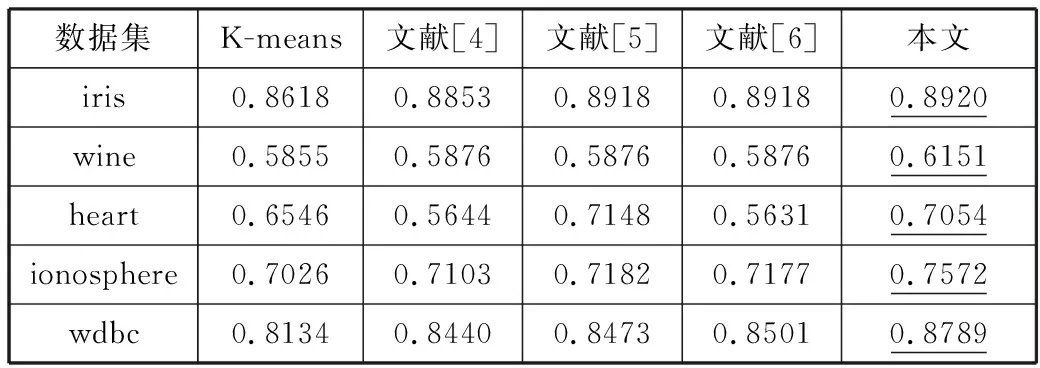
设X={X1,X2,…,Xi,…,Xn}为含有n个数据对象的样本集合,每个样本含有p个属性,Xi={Xi1,Xi2,…,Xip}。现将该集合划分为k个簇,Cluster={Cluster1,Cluster2,…,Clusterk},Cluster∈X,每簇样本个数为m,簇中心集合为Z={Z1,Z2,…,Zk}(k 定义1空间两点间的欧氏距离定义为: (1) 其中,i=1,2,…,n;j=1,2,…,n;w=1,2,…,p。 数据降维方法可以分为2大类,线性和非线性。线性降维法包括多维尺度分析、主成分分析、线性判别分析、独立成分分析和随机投影;非线性降维法包括基于核的主成分分析方法、等距离映射算法、局部线性嵌入算法、拉普拉斯特征映射法等[17]。谱聚类算法是在谱图理论的基础上提出来的一种聚类算法,该算法首先根据距离公式得到样本的空间距离矩阵W,再计算出构造矩阵L,然后对L中的前k个最大特征值所对应的特征向量进行归一化处理,从而在k维空间中形成与原样本的映射关系,达到降维的目的。 定义2样本集X的相似度矩阵为W={Wij|1≤i≤n,1≤j≤n},其中相似性是按照高斯相似度来计算的,即: (2) 定义3对角矩阵D是由空间距离矩阵W的每一列的和构成,即: (3) 定义4构造矩阵L定义为: (4) 定义5簇均值定义为: (5) 其中,i=1,2,…,k。 定义6簇内样本Xj到该簇均值的距离定义为: distMean_X(j)=dXj,mean(i) (6) 其中,i=1,2,…,k;j=1,2,…,m;Xj∈Ci。 定义7簇内各样本到簇均值的距离矩阵定义为: (7) 其中,i=1,2,…,k。 定义8在簇中心更新过程中将与簇内均值距离最小的数据对象Xj作为该簇的中心,Xj满足以下条件: distMean_X(j)=min(distArrayC(i)) (8) 其中,i=1,2,…,k;j=1,2,…,m;Xj∈Ci。 定义9聚类误差平方和E的定义为: (9) 其中,Xij是第i簇的第j个数据对象,Zi是第i簇的中心。 Step1降维。 a)根据式(1)计算样本集X中各数据对象之间的距离; b)根据式(2)构建样本集X的空间距离矩阵W; c)根据式(3)、式(4)构造矩阵L; d)选取L的前k个最大特征值所对应的特征向量x1,x2,…,xn,构造矩阵Xnew=[x1,x2,…,xn]∈Rn×k; e)对矩阵Xnew的行向量进行归一化处理,得到矩阵X′; Step2选择初始聚类中心。 a)根据式(2)构建样本集X′的空间距离矩阵Wnew; Step3更新簇中心。 a)根据式(1)计算样本集X′中各数据对象与Z中各中心点的距离,并按最小距离将各对象划分至最近的簇中; b)根据式(5)~式(7)得到簇内各样本到簇均值的距离矩阵distArrayC; c)根据式(8)从distArrayC中查询当前簇内到簇均值距离最小的数据对象,并将其作为簇中心存入新的簇中心集合Z′中; d)重复Step3中的步骤b、c,更新各簇的中心,直到|Z′|=k,再用Z′取代Z; Step4分配数据。 a)将样本集X′中的数据对象划分到与其距离最近的簇中; b)根据式(9)计算聚类结果评价指标,判断是否收敛,如果收敛,则聚类算法结束,否则转到Step3继续执行。 K-means算法的时间复杂度为On×k×T,n是数据集样本个数,k是聚类个数,T是算法每次运行时簇中心更新的迭代次数。本文算法的时间复杂度具体为On2+n×k×t,与K-means相比,在初始聚类中心选择阶段,本文算法用改进的全局中心算法取代传统的随机选取算法,故n2>n,但由于使用了谱聚类的降维方法,这使得算法的运算量在一定程度上有所减少,此外,改进后的全局中心算法使得各初始聚类中心相对分散,同时具有更强的代表性,这使得簇中心在更新过程中可以更加快速地接近真实解,使得迭代次数减少,故t< 本文实验环境为:Intel Core i3-3240 3.40 GHz,8 GB内存,1 TB硬盘,Win7操作系统,实验平台Matlab 2011b。选用iris、heart、wine等5个常用的UCI数据集对本文算法进行测试,各数据集描述如表1所示。 表1 实验数据 本文算法中的相似矩阵是基于高斯核距离的全连接方式,切图采用Ncut,算法实现的伪代码如下: input:(data,K,σ) S=Euclidean(data) W=Gaussian(S,σ) L=D-W L′=normalized(L) EV=EigenVector(L′,K) SelectInitialClusterCenter();//选择初始聚类中心 while(newCenter !=oldCenter) { UpdateClusterCenter()//更新簇中心 } output:K clusters 其中,data为表1中的样本集,K为标准聚类个数,σ为构造W矩阵时的高斯函数参数,控制了函数的径向作用范围。需要特别指出的是,本文将聚类中心点和上次是否完全相同或聚类准则函数是否无变化作为聚类收敛的判断依据。 图1~图5是K-means算法、文献[4-6]算法和本文算法在UCI数据集的聚类准确率、初始中心选择耗时、簇中心更新耗时、迭代次数、聚类总耗时的实验对比结果,其中K-means算法的实验结果为算法运行50次所得的平均值。 本文首先采用purity方法对聚类结果的准确性进行评价,即将正确聚类的样本数与总样本数的比值作为聚类准确率。如图1所示,在聚类准确率方面,本文算法全部优于其他4种算法。 图1 聚类准确率比较 由图2可知,在初始聚类中心选择阶段,本文算法的耗时明显低于文献[4-6],略高于K-means算法,其原因是本文算法降低了整个样本集的维数,使得数据在子空间的结构更加清晰,聚类时的运算量明显减少,故耗时较少。耗时大于K-means算法的原因在于后者随机选择初始聚类中心,计算量较少,因此初始化速度较快,而本文和文献[4-6]对聚类中心的初始选择从距离、密度等不同角度进行了改进,计算量在一定程度上有所增加,耗时也相对增加。 图2 初始中心选择耗时比较 由图3可知,在簇中心更新阶段,本文算法的耗时不仅小于文献[4-6],更小于传统K-means算法,这说明选取与簇均值距离最近的数据对象作为簇中心,可以更直接地反映出数据对象的具体位置,更准确地反映数据集的整体分布情况。此外,除样本集wdbc外,文献[4-6]的耗时明显小于传统K-means算法,这是因为前者在上一阶段筛选出的聚类中心基本体现了数据对象的大致分布,从而减少了本阶段的迭代次数(结果详见图4),故耗时减少。 图3 簇中心更新耗时比较 如图4、图5所示,与其他4种算法相比,本文算法迭代次数少、收敛速度快、总耗时短,这是由于K-means算法的随机性导致准则函数易陷入局部极小、使得总迭代次数与总耗时同时增加,而文献[4-6]虽然对初始聚类中心的选择进行了改进,但簇中心的更新依然沿用均值中心算法,这使得中心点的选择代表性较差,因此迭代次数及总耗时都大于本文算法。 图4 迭代次数比较 图5 聚类总耗时比较 关于算法聚类结果的评价,除采用常用的聚类准确率、迭代次数和各阶段聚类耗时之外,还采用3个外部评价指标:Rand指数、Jaccard系数和Adjusted Rand Index参数[18]对聚类结果进行比较分析。 3个评价指标的定义如下:设U和V分别是关于数据集的2种划分,其中U是已知的正确划分,而V是通过某种聚类算法得到的划分结果,定义a、b、c、d这4个参数。设a为在U和V都在同一类的样本对数目;b表示在U中为同一类,而在V中却不在同一类的样本对数目;c表示在V中为同一类,而在U中却不在同一类的样本对数目;d为U和V都不在同一类簇的样本对数目。a+b+c+d=n(n-1)/2,其中,n为数据集中所有样本数,即数据集的规模。 设M=a+b+c+d,则M表示所有可能的样本对。Rand指数、Jaccard系数和Adjusted Rand Index参数的定义如下: Rand指数:R=(a+d)/M Jaccard系数:J=a/(a+b+c) Adjusted Rand Index参数: RI=2(ad-bc)/[(a+b)(b+d)+(a+c)(c+d)] 其中:R表示Rand指数;J表示Jaccard系数;RI表示Adjusted Rand Index参数。 从定义可知,Rand指数表示聚类结果与原始数据集样本分布的一致性;Jaccard系数表示实现正确聚类样本对占聚类前或后在同一类簇样本对的比率;RI值越大表示实现正确聚类的样本对越多,聚类效果越好(其上界为1,表示聚类结果与原始数据集的样本分布完全一致;下界为-1,表示聚类结果与原始数据集的样本分布完全不一致)。 观察表2~表5的Rand指数、Jaccard系数、Adjusted Rand Index参数和F值的对比结果可知,本文算法在UCI的5个数据集上的聚类外部评价指标全部优于其他4种算法,尤其在特征维度相对较多的ionosphere和wdbc数据集上,本文算法的优势更为突出。 表2 Rand指数比较 表3 Jaccard系数比较 表4 Adjusted Rand Index参数比较 表5 F值比较 从上述UCI数据集的对比实验结果可以得出:本文算法在多种聚类结果的评价指标中展现出更佳的聚类质量、更快的收敛速度和更高的稳定性,尤其在对较高维度数据聚类时,相比其他3种改进算法,新算法的聚类质量更为理想。 本文将聚类算法的整体性能提升作为研究目标,采用谱聚类算法降低了数据集的特征维度,用全局中心法完成对最大距离法的改进,得到了具有良好分散性的初始聚类中心,在簇中心更新阶段,将均值最近点作为簇中心,降低了迭代次数,减少了算法的运算时间。对比测试表明,本文算法对聚类中心的选取合理、有效,尤其在对高维数据进行聚类时,本文算法的聚类质量更加理想。在实验中发现,在中小规模数据集上本文算法的收敛速度明显优于K-means算法,但随着数据集规模的增大,选择初始聚类中心阶段所消耗的时间呈指数上升,下一步工作将以提高算法的聚类质量为研究目标,同时兼顾算法的时间性能,寻求更为合理高效的聚类方法。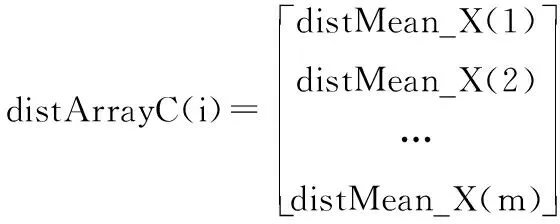
2.2 算法描述
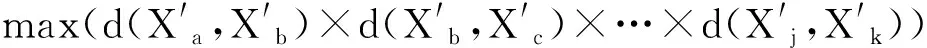
2.3 算法复杂度分析
3 实验结果与分析

3.1 算法的实现
3.2 聚类准确率和时间性能分析
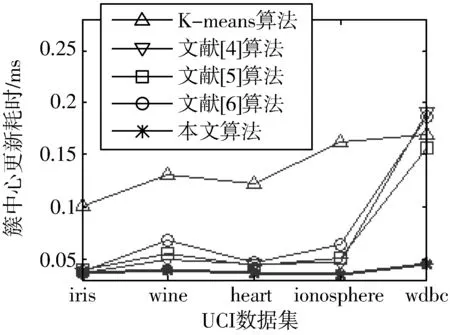
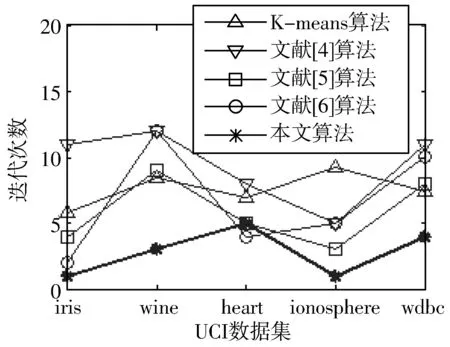
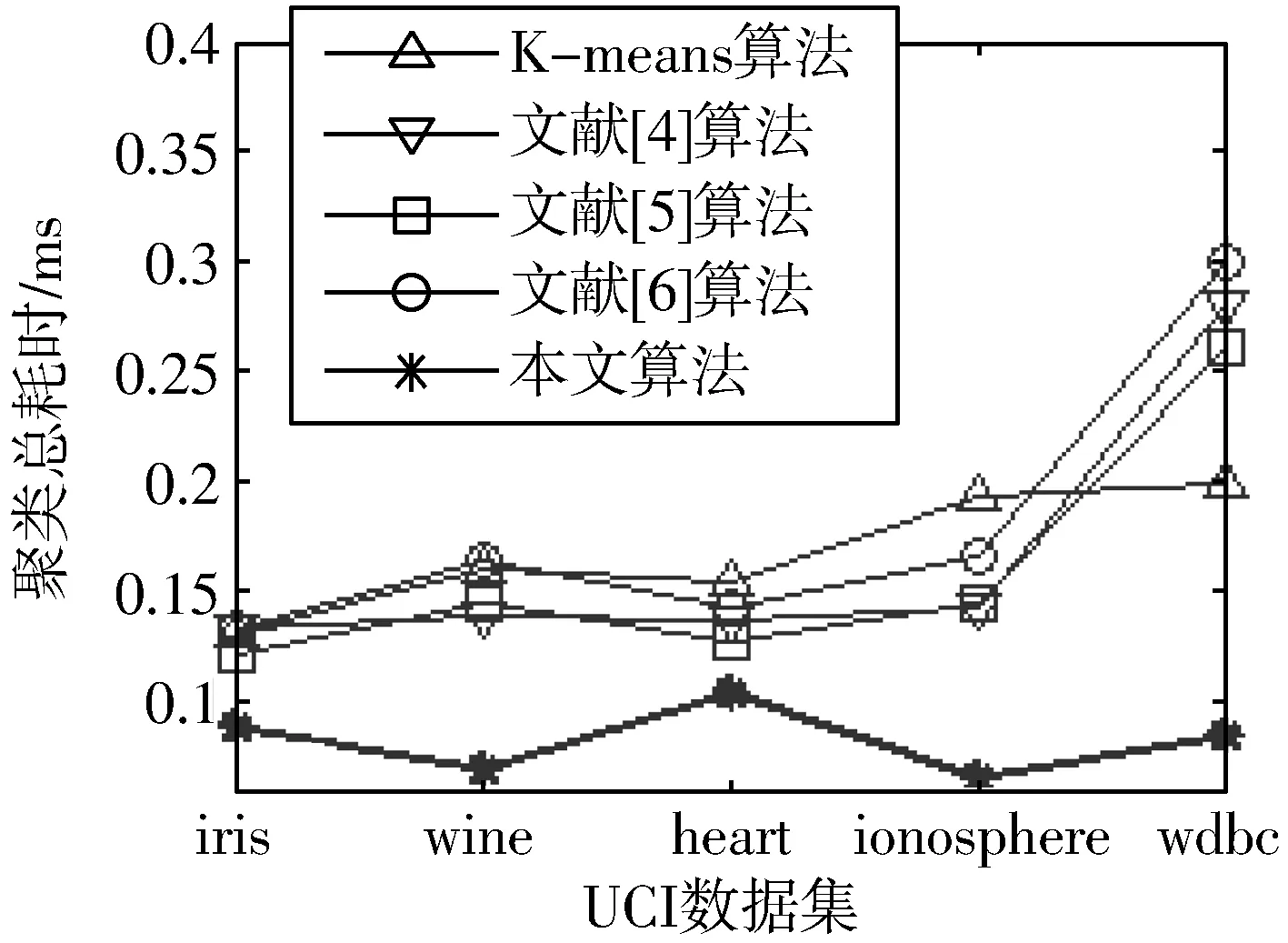
3.3 其他外部评价指标结果


4 结束语
