空孔-裂纹偏置方式对PMMA冲击断裂动态行为的影响

杨仁树， 陈 程， 赵 勇， 丁晨曦， 苏 洪， 郑昌达

(1. 中国矿业大学(北京) 力学与建筑工程学院，北京 100083； 2. 中国矿业大学(北京) 深部岩土力学与地下工程国家重点实验室，北京 100083)

材料在承受动载以后会产生相应的损伤，甚至会发生动态断裂引起材料力学性能失效，材料动态特性的研究一直是学者们的研究热点。在工程实践中，遇到最多的材料就是天然岩体，在这种材料中会存在大量的孔洞、节理等缺陷，这些缺陷的存在对于材料的动态力学及断裂特性有重要影响。因此，对于含缺陷介质中动态裂纹的扩展具有重要的科学与工程意义。姚学锋等[1-2]分析了单偏置裂纹的尖端复合应力场以及对不同偏置距离的裂纹起裂时间进行了对比分析；研究了拉伸载荷下两交错偏置平行裂纹的相互作用，分析了两偏置平行裂纹的起裂和传播行为。岳中文等[3-5]利用数字激光焦散线实验方法研究了带双裂纹梁在冲击载荷下的动态特性、空孔位置对裂纹扩展轨迹以及裂纹起裂时间影响、运动裂纹与不同倾角缺陷之间的相互作用机理。杨立云等[6]研究了主裂纹与次裂纹之间的相对距离对主裂纹起裂时间以及最大扩展速度的影响。杨仁树等[7-8]分析得到预制裂纹倾角的增大会使得主裂纹的扩展轨迹发生偏转；圆形空孔对运动裂纹的扩展速度和应力强度因子有抑制作用，而且孔径越大这种抑制作用也越大。李清等[9-10]研究了半圆盘构件在冲击载荷作用下预制裂纹倾斜角度的改变引起的混合型裂纹起裂和扩展的动态特性；研究了冲击载荷下单裂纹与双裂纹在冲击载荷作用下裂纹扩展动态参数的变化规律。丁晨曦等[11]研究了不同倾角裂纹缺陷对运动裂纹扩展的导向作用和抑制作用。左建平等[12]利用扫描电镜(SEM)方法实时获取了三点弯加载中裂纹扩展高倍率照片，并指出偏置缺口位置影响岩石断裂区域的应力状态。

这些学者从不同的角度对裂纹或空孔的偏置以及裂纹与空孔缺陷之间的相互作用进行了相应的分析。然而，较少对比分析了空孔与裂纹偏置方式的改变对裂纹起裂以及扩展形态的影响，在相关方面的研究还有一些不足。本文利用动态焦散线实验系统结合同步控制系统对裂纹与空孔偏置方式对裂纹的起裂模式、偏转规律和扩展形态的影响机制进行了研究，分析了偏置方式的不同对裂纹扩展方向与路径、裂纹的扩展速度、动态应力强度因子等因素的影响。

1 裂纹偏转和裂纹尖端混合型应力强度因子

1.1 裂纹偏转

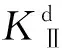
(1)

μ表示应力强度因子比例系数， 其可以由焦散线对称轴相对于裂纹轴的角位移φ来确定，其表达式为

(2)

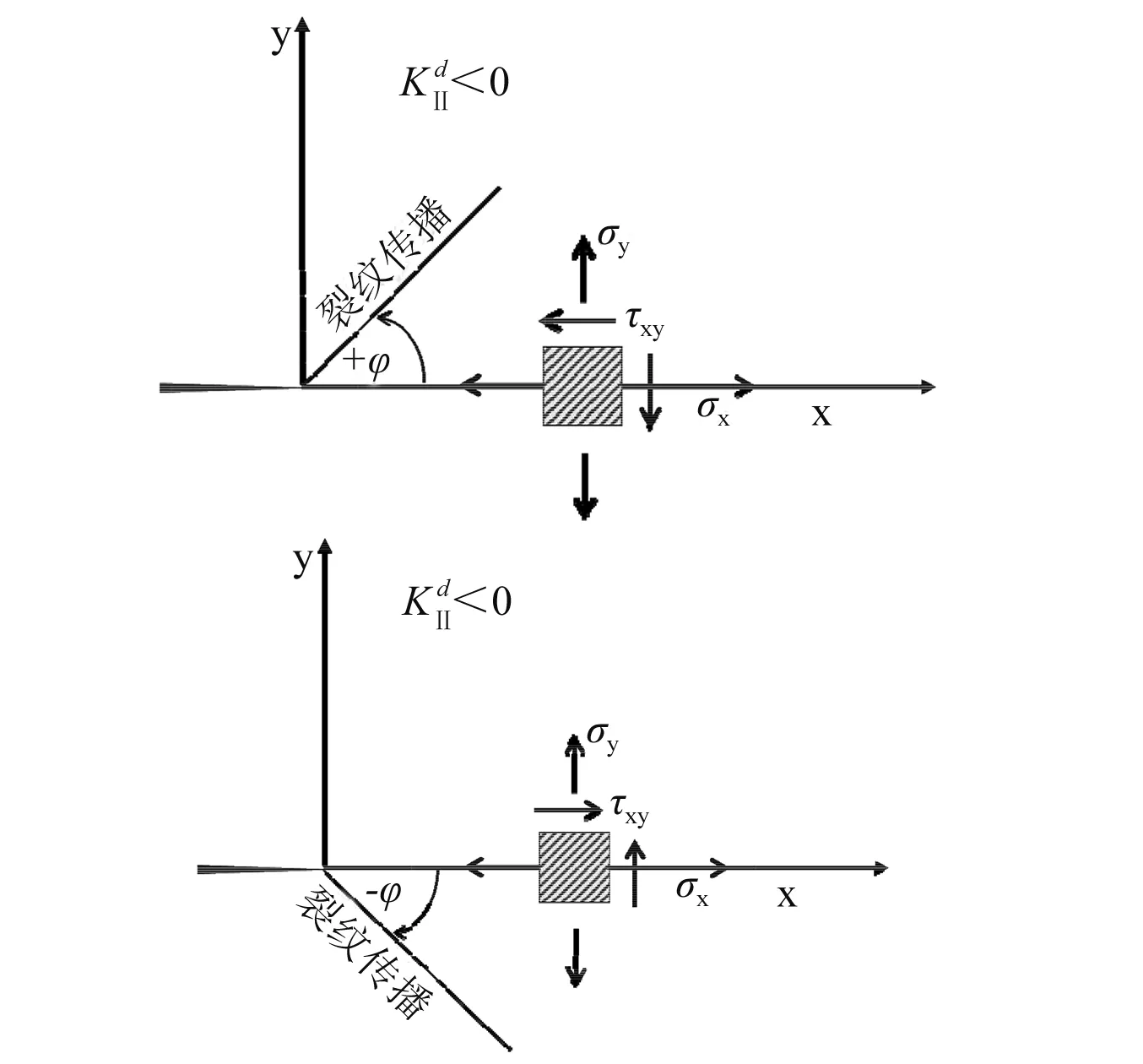
图1 平面混合载荷裂纹偏转[13]Fig.1 Crack deflection angle under plane mixed-mode loading[13]

1.2 混合模式下裂纹尖端焦散曲线

文献[15-17]推导给出了裂纹尖端混合应力强度因子的参数方程表达式如下

(3)

式中：ε表示常数，实验中采用的是透射式焦散线光路取值为1；z0表示试件中面距相机对焦平面距离，实验中取值为90 mm；d表示试件厚度；Cr,t,f表示应力光学常数；λm表示光束放大系数，实验中使用的是平行光取值为1；r表示焦散线初始曲线半径。

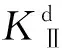
图2 混合模式下的裂纹尖端焦散曲线Fig.2 Crack tip caustics curve under mixed mode loading

2 数字激光动态焦散线实验

2.1 件尺寸及实验方案

本实验选用的模型材料是有机玻璃板(PMMA)，该材料具有光学各项同性且其焦散光学常数较高。试件的动态力学参数[18]如表1所示。试件示意图如图3所示，其尺寸(长度×宽度×厚度)L×W×T=220 mm×50 mm×5 mm，空孔直径D=6 mm，空孔中心距试件上边界距离W1=25 mm，试件预制裂纹长度C=10 mm，宽度为0.6 mm。支点距试件边缘的距离L3=20 mm，也即支点1和支点2之间间距为180 mm。实验设计2种方案，每种方案3个试件：空孔中心位于试件中间位置即L1=110 mm，预制裂纹裂纹偏移试件中心位置右侧5 mm即L2=115 mm，记为试件S-1；预制裂纹位于试件中间位置即L2=110 mm，空孔中心偏移试件中心左侧5 mm即L1=105 mm，记为试件S-2。

实验中使用的动态焦散线光路系统如图4所示。高速相机采用Photron公司生产的Fastcam-SA5(16G)高速相机，实验中高速相机拍摄频率为105fps。采用同步控制技术进行数据的自动采集与记录，用信号线将落锤、冲击加载头与高速相机相连接以形成一个断-通信号回路，落锤与冲击加载头接触的瞬间会产生一个断通信号，该断通信号经过信号线传输给高速相机，并作为触发信号立即激发高速相机进行焦散图像的动态采集和记录。

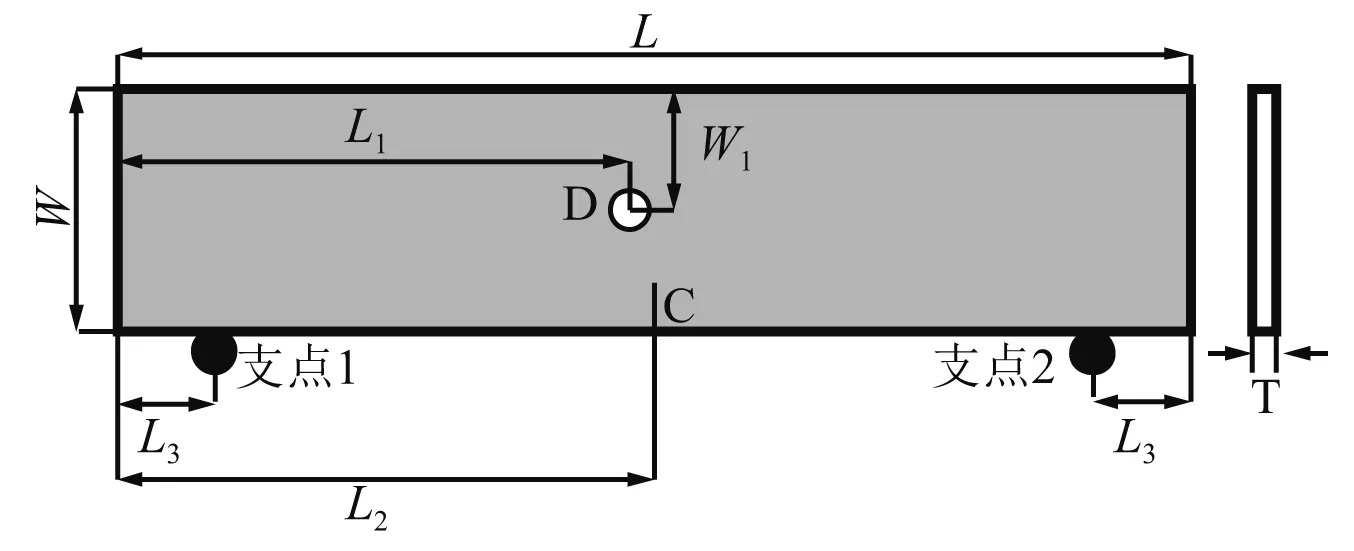
图3 试件模型示意图Fig.3 Sample size diagram

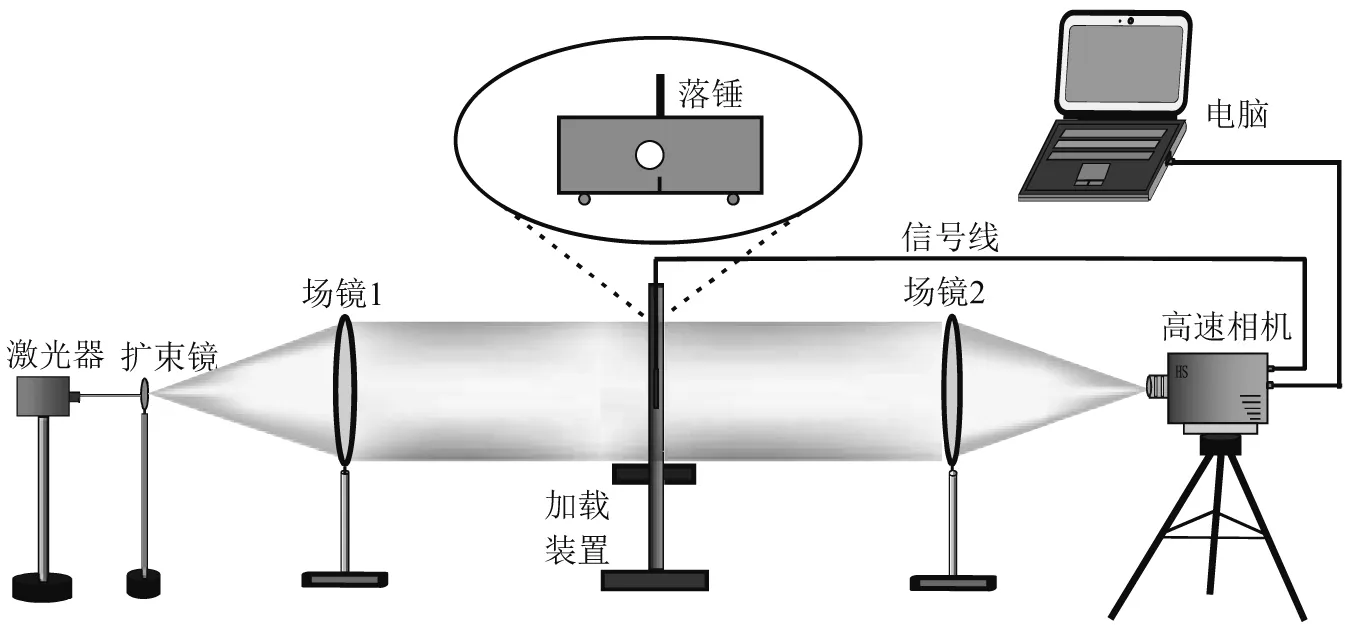
图4 实验光路图Fig.4 Experimental optical system diagram

表1 PMMA试件动态力学参数Tab.1 Dynamic mechanical parameters of PMMA specimens

3 试验结果及分析

3.1 裂纹扩展轨迹

图5为试件S-1，S-2实验结果，其中裂纹A1和裂纹A2分别表示试件S-1圆孔下方与圆孔上方裂纹，裂纹B表示试件S-2中扩展裂纹。坐标轴原点定义在初始预制裂纹尖端，裂纹偏转角度正负值的定义与图1中定义相同。通过对试件S-1与S-2中的裂纹扩展路径进行数值化后处理得到图5(c)。

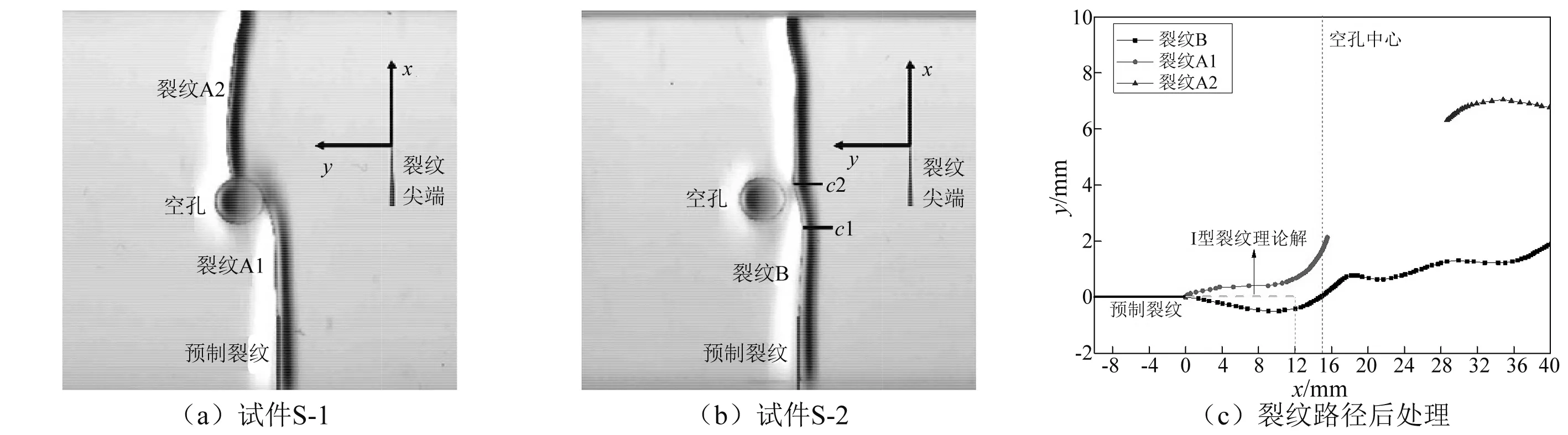
图5 实验结果Fig.5 Patterns of experimental results

3.2 裂纹焦散斑变化图

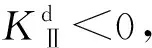
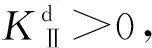
3.3 裂纹扩展速度变化规律

图7为试件S-1，试件S-2运动裂纹扩展速度随时间变化曲线。由图7(a)可知，试件S-1中裂纹A1扩展速度呈先增大后减小的趋势。预制裂纹在t=120 μs时起裂，起裂速度为74.1 m/s，随后裂纹扩展速度不断增加，在t=160 μs时达到最大值222.2 m/s，然后裂纹扩展速度不断减小，在t=200 μs时裂纹扩展速度降为0 m/s，此时运动裂纹与空孔贯通裂纹止裂。随着时间的推移，能量在空孔处不断积累，裂纹A2在空孔处再次起裂并传播。裂纹A2在t=520 μs时起裂，起裂速度为463 m/s，并且该速度大于不仅大于裂纹A1的起裂速度还大于该裂纹的峰值速度222.2 m/s。裂纹A2起裂之后，其扩展速度呈递减的趋势。但当裂纹A2运动至试件S-1上边界附近裂纹扩展速度出现振荡。在t=590～640 μs时间段内，裂纹A2扩展速度在76.4 ～18.5 m/s范围内振荡。在t=650 μs时裂纹扩展速度降为0 m/s，裂纹贯穿整个试件S-1。

图6 运动裂纹与空孔相互作用动态焦散图Fig.6 Interaction of running crack with hole

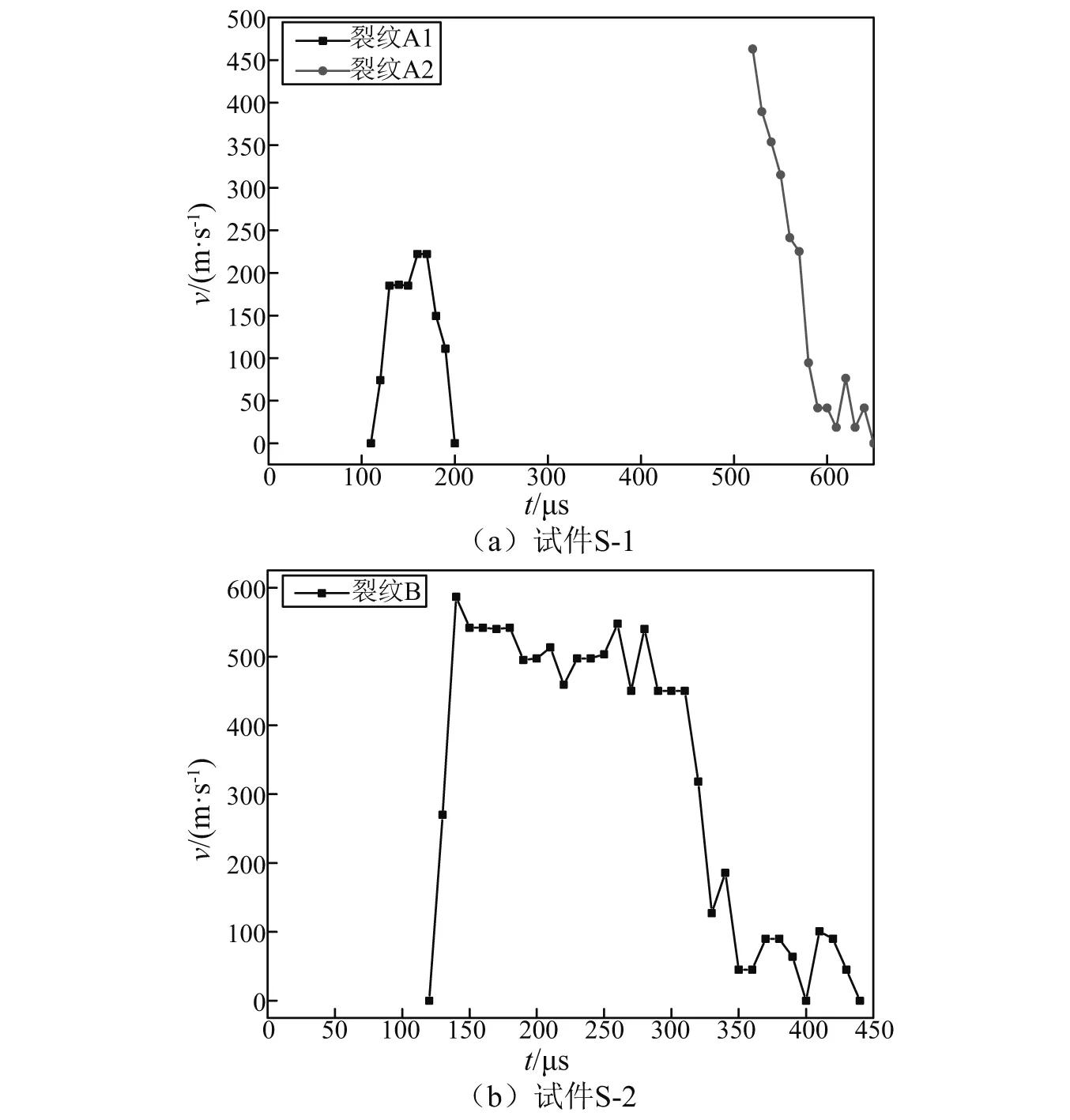
图7 运动裂纹扩展速度-时间曲线Fig.7 Curves of crack growth velocity vs. time

由图7(b)可知，试件S-2中裂纹B扩展速度呈先增大然后振荡最后不断下降的趋势。预制裂纹在t=130 μs时起裂，起裂速度为270 m/s，随后裂纹扩展速度急剧上升，在t=130 μs时达到峰值586.7 m/s。在t=130～310 μs时间段内裂纹扩展速度在450～547.4 m/s的范围内不断振荡，出现震荡的原因是由于运动裂纹受到空孔边界处反射应力波的作用。结合图6(b)中焦散图像在t=190～260 μs时间段内，空孔对运动裂纹先吸引然后排斥，在该阶段裂纹B扩展速度呈现先增大后减小然后再增大的趋势，在t=220 μs裂纹扩展速度达到极小值458.9 m/s，这也对应由吸引向排斥过渡的转折点。在t=310 μs以后，裂纹B扩展速度快速降低。随着裂纹B的不断运动，其与试件S-2上边界相对距离的不断减小，裂纹B受边界反射波的影响增加，裂纹扩展扩展速度在0 ～100.6 m/s范围内波动，直至裂纹停止，试件S-2一分为二。

3.4 裂纹尖端应力强度因子变化规律

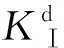
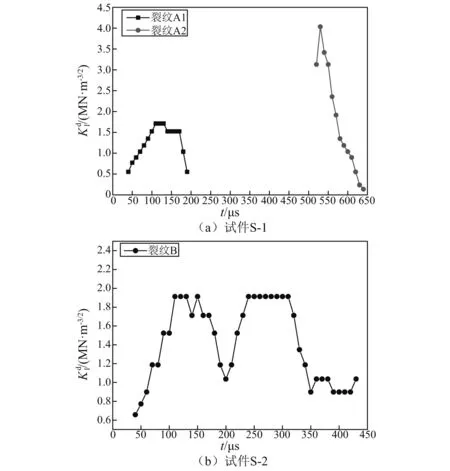
图8 动态应力强度因子-时间曲线Fig.8 Curves of dynamic stress intensity factor vs. time

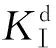
4 结 论

利用动态焦散线的实验方法研究了空孔-裂纹偏置方式对PMMA冲击断裂动态行为的影响，通过对数据的分析得到以下结论：

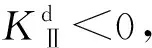
(2) 在预制裂纹与空孔中心相对距离为5 mm情况下，当预制裂纹偏置时，裂纹与空孔贯通，裂纹在空孔上边界出现二次起裂现象；当空孔偏置时，裂纹未与空孔贯通。

(3) 当预制裂纹偏离中心位置时，裂纹受力的不对称性以及裂纹与空孔的相互作用，使得空孔对裂纹的作用表现为吸引，裂纹扩展路径呈抛物线型；当空孔偏离中心位置时，由于空孔的偏置使得裂纹尖端应力场由纯Ⅰ型转变为Ⅰ型和Ⅱ型复合型，同时空孔对裂纹的作用表现为先排斥后吸引再排斥，裂纹扩展路径呈S型。

(4) 裂纹与空孔的贯通从时间尺寸上来说起到抑制裂纹扩展的作用，但当裂纹在空孔上边界再次起裂时该裂纹起裂速度和动态应力强度因子都大于预制裂纹第一次起裂相应的值，这样反而加剧了试件的破坏，二次起裂后材料更易造成破坏。