超材料消波混凝土板在二维平面波作用下的削波效应研究
2018-11-01郜英杰范华林金丰年
郜英杰, 范华林, 张 蓓, 金丰年
(1.中国人民解放军理工大学 国防工程学院 爆炸冲击防灾减灾国家重点实验室,南京 210007;(2.南京航空航天大学 机械结构力学及控制国家重点实验室 结构轻量化与智能制造研究中心,南京 210016)
进入20世纪后期,人们对材料的研究不仅仅局限于大自然,而是基于对所需材料的特定性质去设计材料。超材料就是具有人工设计结构的一类新型材料,能够表现出人们所想要的特有的物理性质,因此,自从超材料被提出后,对它的研究一直是一个热门。近些年来,国内外学者对超材料在电磁波,声波领域进行了充分的研究[1-7],提出光子晶体,声子晶体和局域共振型声学超材料概念,并经过大量试验,成功实现三者对电磁波和声波传播的控制。
随后,刘娇等[8]对这种局域共振型声学超材料的机理进行了深入探讨,以通过二维固体板中的弹性波传播为例,证明了在声学超材料中带隙形成既与共振子对波的散射相位有关,也与波在共振体之间的几何传播相位有关。孙宏伟等[9-10]依据这种局域共振系统设计了一种由集中质量和弹性薄膜构成的二维声学超材料板并进行了数值模拟,使之能够对频率为157.5 Hz的机械波进行吸收。
基于此,将超材料结构应用于混凝土中,形成可以消波的超材料混凝土,这种超材料混凝土由砂浆和方阵排列的聚合体组成。在特定频率振动波传播过程中,通过聚合体发生谐振来消耗机械波的能量。本文将通过负有效质量解释这种消波原理,并利用LS-DYNA软件数值模拟分析超材料消波混凝土的消波优势,隔层材料,聚合体大小及聚合体排列方式对消波效果的影响。
1 超材料消波混凝土板的设计
本文提出的这种超材料消波混凝土(Super-Material Wave Absorbing Concrete, SMWAC)板(如图1)由两部分组成,聚合体和砂浆。在铅柱侧面包裹一层软介质形成聚合体,再将这种聚合体均匀排列在混凝土砂浆中,形成SMWAC板。当振动波从其中一侧向另一侧传播时,由于铅柱,软介质,砂浆之间的弹性模量不同,它们之间就会产生振动相位差,从而使机械波能量在三种材料的振动中消耗掉,起到消波的目的。
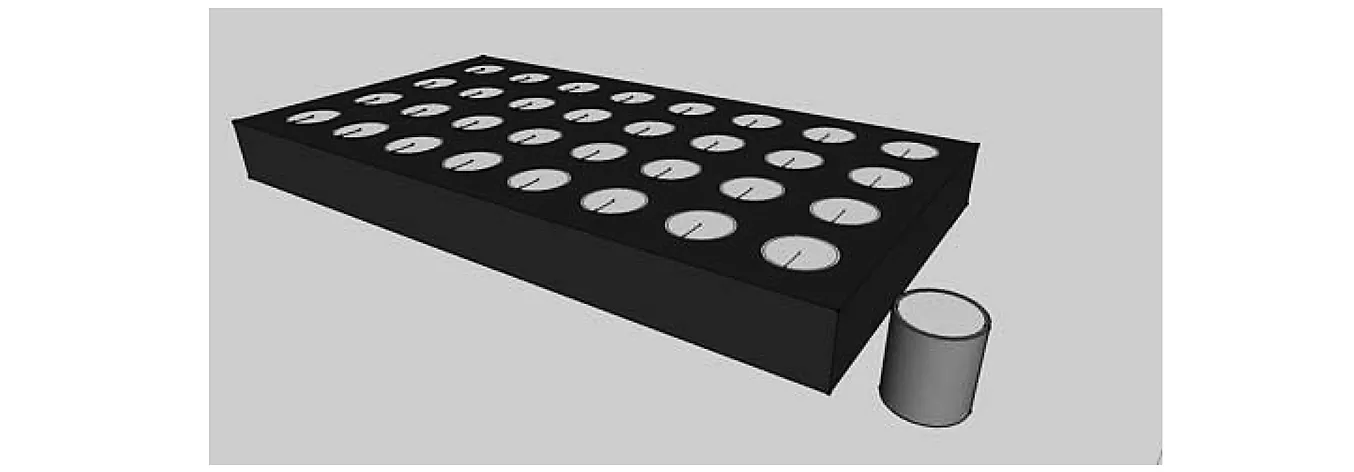
图1 设计的SMWAC板模型示意图Fig.1 Designed SMWAC slab model schematic diagram
2 负有效质量
如图2所示,可以将SMWAC板简化为以下弹簧-质量模型。
铅柱相当于图中小球,软介质相当于弹簧,混凝土砂浆则是最外面的实体。
参照附录,经过推理可以得到振动过程中的负有效质量公式
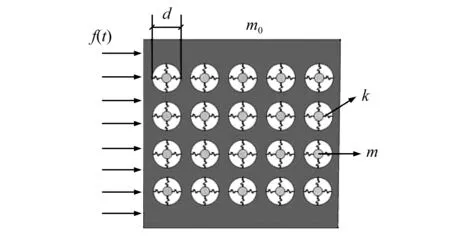
图2 弹簧-质量模型Fig.2 Spring-mass model
(1)
根据式(1),利用Origin软件做出图3所示图形。从该图中可以看到,当1.1≤ω/ωρ≤1.3时,有效质量为负值,即当振动波频率为1.1倍~1.3倍聚合体自振频率时,表现出负有效质量特性,波传播过来时聚合体的振动方向与振动波方向相反,能量相互抵消,因此,可以起到消波效果。
在后文的数值模拟中,应用的聚合体由密度较大的铅柱外面包裹PPS塑料形成,铅柱高50 mm,直径20 mm,PPS塑料层为1 mm厚,SMWAC板的各种材料的材料参数在表1中给出。

表1 模型材料参数Tab.1 Parameters of model material
根据自由振动理论可知,SMWAC板的自振频率为
(2)
(3)
式中:k是隔层材料弹性系数,m为铅柱质量。
假设隔层为均匀弹性材料,则k与E的关系为
kt=EA=2πERll
(4)
式中:ρPb是铅柱密度;Rl是铅柱半径;l是铅柱高;t为PPS隔层厚度。
而SMWAC板的自振周期
(5)
将式(2)~式(4)代入式(5),得到
(6)
式中:Rl=0.006 m,l=0.05 m,E=1.0×1010Pa,t=0.000 5 m,ρl=11.34×103kg/m3。代入式(6)中,可以得到,Tρ=10.23 μs。因此,在数值模拟中,对模型施加周期为T=0.8Tρ=8 μs的平面波。
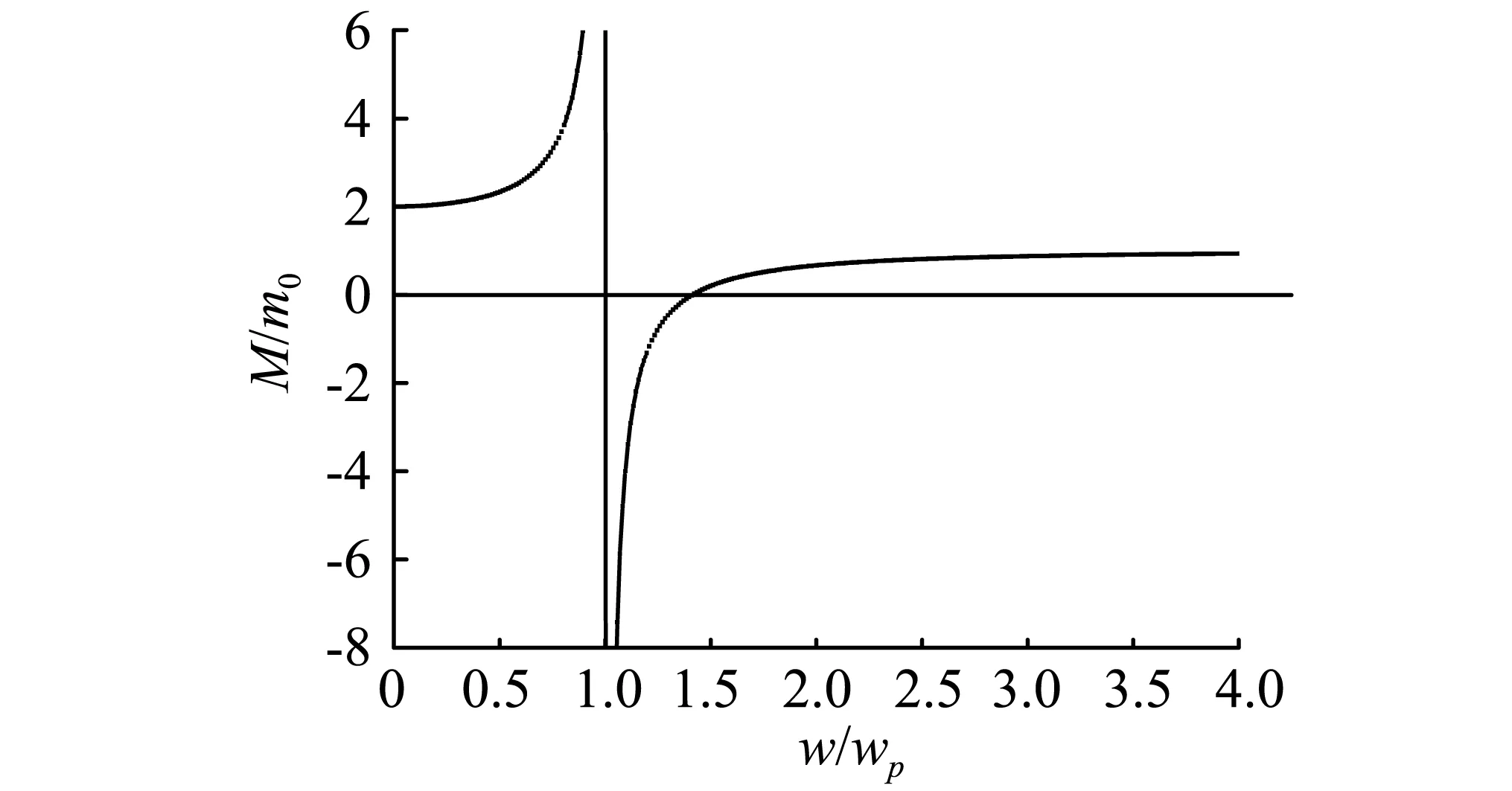
图3 不同频率下的有效质量 Fig.3 Effective mass in different frequency
3 建立模型及数值模拟结果分析
3.1 建立模型
利用LS-dyna软件进行数值模拟,如图4所示,建立120 mm×240 mm×50 mm的SMWAC板模型,在上下两个侧面设置对称边界,消除边界影响,前后面设置固支边界,保证固定板不发生位移,在右面施加振动波,振动波如图5所示。由于模型较大,为了避免计算机动态内存分配空间不足的问题,在保证模型精度影响不大的前提下对模型进行以下简化。在SMWAC板数值模拟中混凝土砂浆和铅柱采用线弹性材料模型,隔层材料采用黏弹性模型,三种材料之间采用共节点方法使之传递力与位移。

图4 SMWAC板模型俯视图Fig.4 The plan view of SMWAC slab model
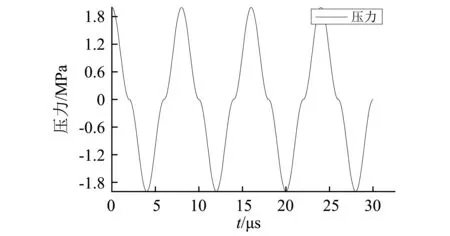
图5 施加的振动波曲线Fig.5 Curve of applied vibration wave
为了研究SMWAC板的消波效果及其影响因素,建立如图6所示的普通混凝土模型与SMWAC板进行对比,观察其消波效果,并分析聚合体隔层材料,聚合体尺寸大小,排列方式等对消波效果的影响。
图6 普通混凝土板模型俯视图Fig.6 The plan view of common concrete slab model
3.2 SMWAC板消波效果
在波的传播路径上依次选取三个点,测量三个点的应力,以此作为分析消波效果的依据。图7是根据A、B、C三点的应力时程曲线最大值画出的SMWAC板和普通混凝土板的应力图。模拟结果表明,对于SMWAC板,在振动波的传播过程中,能量得到了很大的削弱,当波传到中间的时候,应力已经削弱了一个量级,当波传到另一端时,相对初始荷载,应力削弱了两个量级。而对于普通混凝土,在波的传播过程中,到达另一边时,能量只是削弱到初始的六分之一,相对比,SMWAC板明显削弱了波的传播。
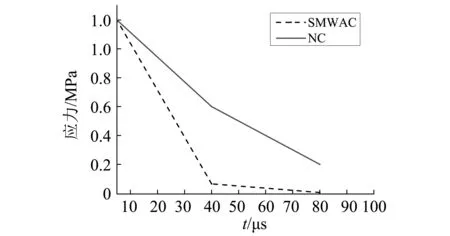
图7 普通混凝土板(NC)与SMWAC板三点应力图Fig.7 Three-point stress diagram ofcommon concrete slab and SMWAC slab
为了进一步分析SMWAC板的削弱机理,统计SMWAC板中各部分能量,如图8所示。从应力云图可以看出,在输入的所有能量中,大部分的能量都分布在了铅柱内,混凝土砂浆只承受了一少部分能量。
从能量分布图看,聚合体铅柱中的能量占到了整体能量的70%,混凝土砂浆只承受了很小一部分振动波能量。根据第2节中的理论,大部分能量消耗在铅柱在聚合体中的振动上。因此,在特定频率的施加荷载作用下,相比较于普通混凝土板,SMWAC板能对砂浆起到更好的保护作用,并且使平面波在板的传播过程中得到明显衰减,从而起到消波效果。
3.3 隔层材料对SMWAC板消波效果的影响
第2节分析了SMWAC板的消波原理,并根据模型中隔层材料的弹性模量考虑施加合适的平面波,得到了较好的消波效果。根据负有效质量原理,当模型中的隔层材料改变后,在原有平面波作用下,SMWAC板的消波效果将会削弱。为了验证该猜想,将隔层材料改用LDPE材料,两种材料的参数在表2中给出。在隔层为LDPE材料的SMWAC板中,依旧施加周期为8 μs的平面波,在相同位置取A,B,C三点测量其应力大小,与隔层为PPS的SMWAC板进行对比,得到表3所示的结果,为了详细对比两者的削波能力变化,根据模拟结果做出模型各部分能量分布图(如图9所示)。从表3的数据对比看出,LDPE隔层的SMWAC板消波效果与PPS隔层的SMWAC板接近。而从能量分布图中看,隔层为LDPE的SMWAC板中混凝土砂浆所吸收的能量超过了铅柱所吸收的能量,即聚合体并没有有效吸收振动波能量从而起到保护砂浆的作用。因此,这种结果验证了之前的猜想,带有隔层材料的SMWAC板在某个特定频率范围的平面波作用下具有明显的消波效果,当更换隔层材料后,面对同样频率的平面波,就发挥不出好的消波能力,即SMWAC板具有选择性消波特性。

(b) 能量分布图图8 SMWAC模型能量分布图及应力云图(A——铅柱;B——隔层;C——混凝土)(下文能量图中A、B、C与本图意思一样)Fig.8 Energy distribution of model and stress nephogram

表2 隔层材料参数对比Tab.2 Comparison of coating material parameters
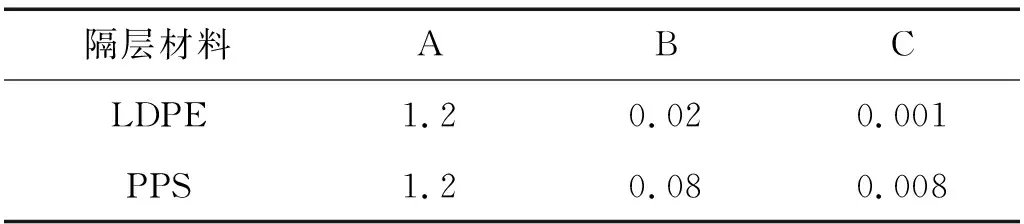
表3 两种材料的SMWAC板三点应力对比Tab.3 Three-point stress comparison of SMWAC slabs with two materials MPa
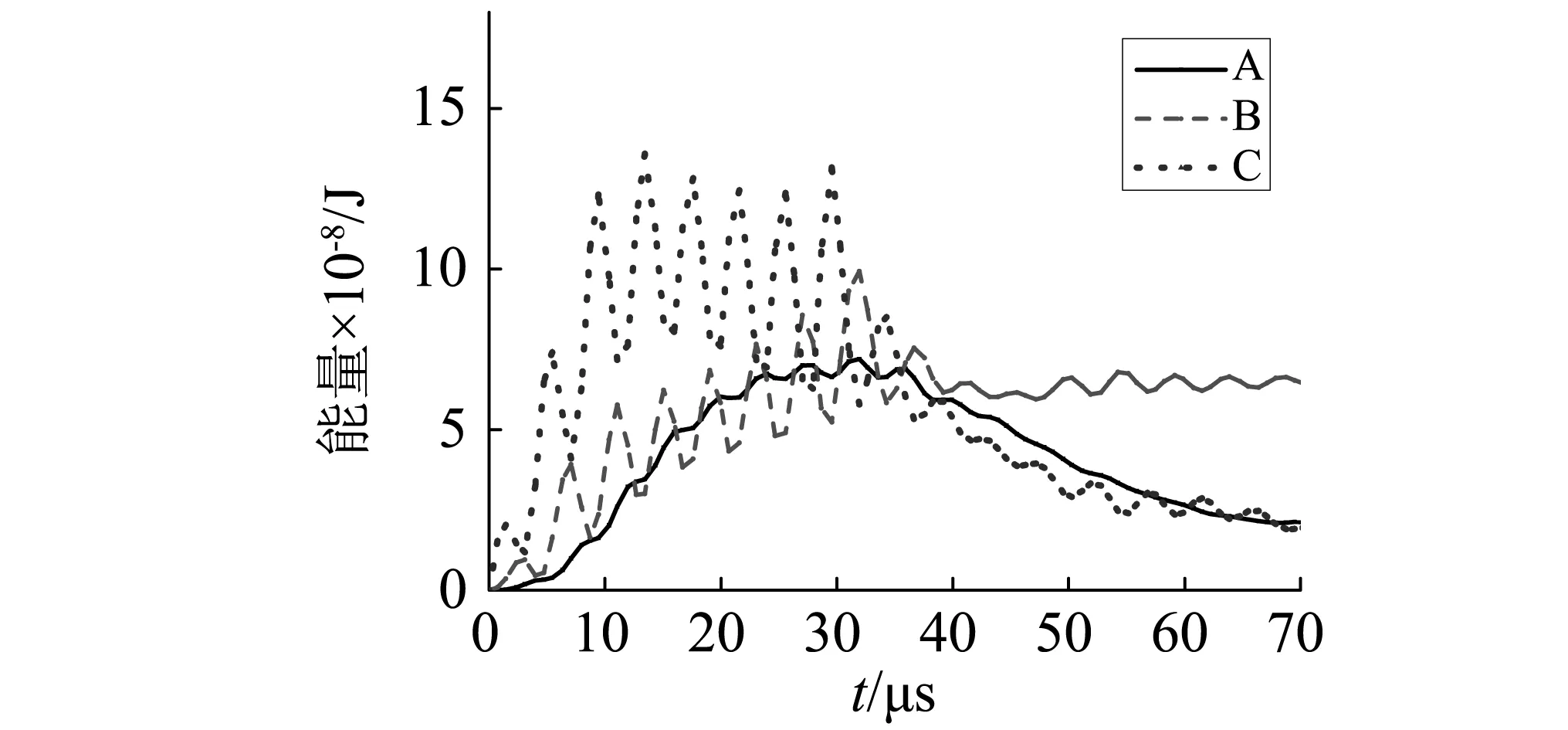
图9 隔层为LDPE的SMWAC板能量分布Fig.9 Energy distribution of SMWAC slab with LDPE coating
3.4 尺寸大小对SMWAC板消波效果的影响
在前文的SMWAC板模型基础上,将聚合物尺寸扩大一倍,则聚合物排列的密度就会减小,虽然隔层材料不变,但是由于板的结构发生变化,因此对SMWAC板的消波效果会产生影响。探究聚合体尺寸大小对SMWAC板消波效果的影响,可以为日后在同等用料下采取何种尺寸达到最优消波效果提供参考。
为此,设计三种聚合体尺寸,并对三种SMWAC板施加模拟爆炸荷载,进行数值模拟,爆炸荷载曲线见图10。三种聚合体尺寸如表4所示,在三种模型中各种材料所占的比重相同,以此来观察不同尺寸对SMWAC板消波效果的影响。根据模拟结果,做出三种模型的A、B、C三点应力图,如图11所示。
图11表明,三种SMWAC板均在爆炸波传播中起到明显的削弱作用,对于尺寸最小的normal模型,当平面波从A点传到B点后能量削弱了一大半,到C点又进一步削减为初始能量的四分之一;对于big模型和biggest模型,当波传到B点时能量就已经削减为初始值的四分之一,当到达C点时,波在biggest模型中又消耗了大半能量,效果优于另外两种尺寸的SMWAC板。对三种模型进行对比发现,在保证SMWAC板中各种材料比例不变的情况下,施加同样的爆炸冲击波,聚合体尺寸较大时,消波效果较明显。
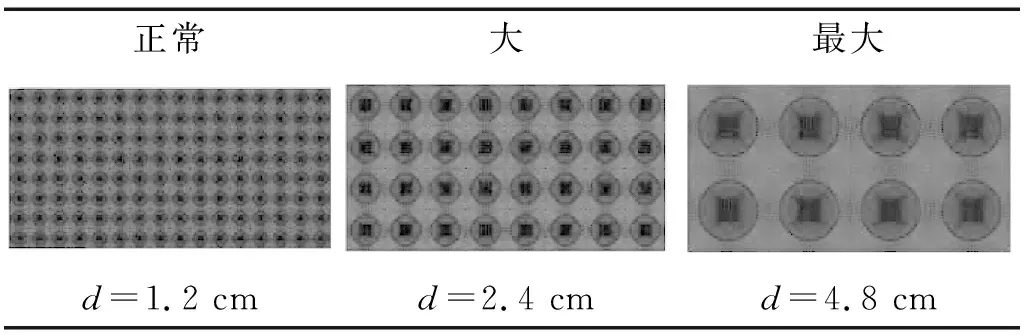
表4 三种聚合体尺寸对比Tab.4 The contrast of three aggregate sizes
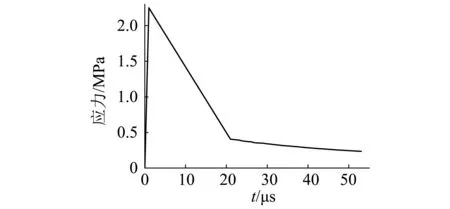
图10 爆炸波曲线Fig.10 Blast wave curve

图11 三种尺寸的SMWAC板中三点应力对比Fig.11 Three-point stress comparison of SMWAC slabs of three kind of size
3.5 排列方式对SMWAC板消波效果的影响
之前进行的模拟都是将聚合体在混凝土中矩阵排列,而其他排列方式是否会影响到SMWAC板的消波效果还不知晓,为了对其探究,本节对比了矩阵排列和交错排列所组成的SMWAC板的消波效果。
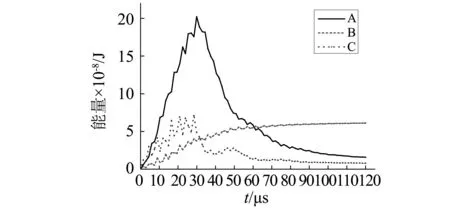
建立如图12所示的两种模型进行对比。根据模拟结果,做出A、B、C三点的应力表如表5所示,两个模型的能量分布图如图13。
从三点应力图看,两种排列方式的消波效果几乎没有差别;从能量分布图看,两种SMWAC板能量分布图走势也近乎相同。综上分析,两种SMWAC板的消波效果几乎没有差别,可以初步猜想聚合体排列方式对SMWAC板的消波效果影响不大,为后续研究无序排列方式是否会影响到SMWAC板消波效果打下基础。

交错排列

矩形排列图12 交错排列方式和矩形排列方式Fig.12 Permutation of interlacement and rectangle
交错排列
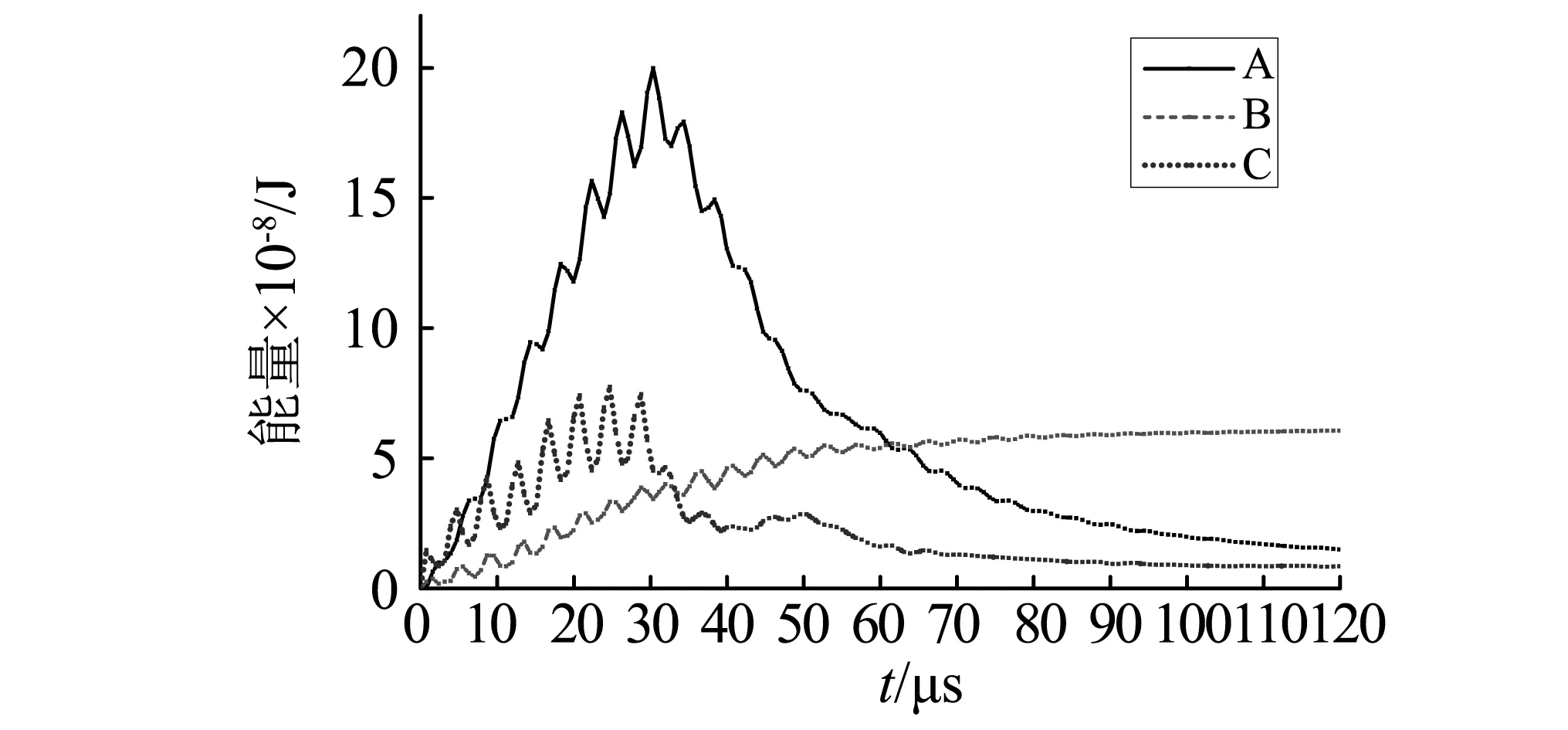
矩形排列图13 两种排列方式的能量分布图Fig.13 Energy distribution of two permutation

表5 两种模型三点应力对比Tab.5 Three-point stress comparison of two modelsMPa
4 结 论
本文提出了一种超材料消波混凝土板(SMWAC板),并对其消波效果进行理论分析和数值模拟。通过数值模拟与结果分析,得出以下结论:
(1) 相比普通混凝土板,SMWAC板能够对机械波进行有效的削弱,并更好地保护混凝土砂浆。
(2) SMWAC板具有选择性消波特性,通过改变聚合体中隔层材料,可以使SMWAC板削弱不同频率段的机械波。
(3) 在同一爆炸波作用下,当SMWAC板中各材料比例不变时,聚合体尺寸较大时,SMWAC板能够更充分地发挥消波能力。
(4) 本文考虑了两种排列方式进行消波效果的比较,发现差别不大,由此初步推测排列方式的不同对SMWAC板的消波效果影响不大,对后续进行无序的排列方式是否会影响SMWAC板的消波效果奠定基础。
