基于非线性增益递归滑模的船舶轨迹跟踪动态面自适应控制

沈智鹏 张晓玲

具有动力定位系统的三自由度全驱动海洋工程船舶通过对船舶推进器的精确控制,可使船舶以一定姿态保持在海面某一固定位置或精确地跟踪某一设定轨迹,以完成深海勘探、海底管道建设、海上石油钻探和供给等工程领域作业.轨迹跟踪属于广义上的动力定位,轨迹跟踪技术的理论挑战和海上新兴应用需求的增长,使得相关人员对船舶轨迹控制的研究给予了极大的关注.

鉴于船舶运动方程的非线性特性,Fossen等[1]提出的反演法可有效避免对船舶模型进行线性化的要求,构造中间虚拟控制量逐步回推获得控制律,得到闭环系统全局指数稳定.船舶在航行过程中不可避免地遭受来自外部环境扰动,例如风、浪、流等的影响,反演法与其他控制方法相结合也取得了一定的研究成果.Yang等[2]采用扰动观测器对外部环境扰动进行估计并补偿,结合反演法和李雅普诺夫理论,实现船舶轨迹跟踪;付明玉等[3]引入自适应与反演法结合进行控制律设计,其中自适应控制项实现扰动参数的在线更新,增强鲁棒性,实现协同路径跟踪.而在被控对象相对阶增长的高阶系统情况下,传统反演法对虚拟控制量求导引起的计算膨胀给控制器设计带来不便.为解决这个问题,Swaroop等[4]首次提出动态面控制(Dynamic surface control,DSC)方法,引入一阶低通滤波器避免对虚拟控制量的求导,简化计算,易于工程实现;杜佳璐等[5]将动态面控制技术融合到反演法中,并设计自适应律对未知外部环境扰动的界进行估计,增强鲁棒性,实现船舶的动力定位.

在上述研究过程中,需要已知精确的模型相关参数以确保控制性能,而实际情况下是很难实现的.许多新的智能控制方法,由于学习和适应的近似能力,不需要花费很多精力进行系统建模,被广泛应用于各类控制问题中.Wang等[6]采用径向基(Radial basis function,RBF)神经网络(Neural network,NN)逼近系统不确定项,设计神经网络自适应动态面控制器;Xu等[7]采用最小参数学习法减少计算负担,结合动态面技术,通过小增益定理证明超高速飞行器良好的跟踪性能.刘希等[8]引入递归滑模解决常规动态面对低通滤波器时间常数和神经网络自适应参数摄动脆弱的缺点,得到闭环系统所有状态半全局一致最终有界.考虑船舶模型参数未知、具有未建模动态和风浪流等环境扰动,贾鹤鸣等[9]采用非线性迭代滑模对无人水下航行器(Unmanned underwater vehicle,UUV)进行航迹跟踪控制,无需对系统模型不确定部分和海流干扰进行估计,避免舵的抖振、减小稳态误差与超调;沈智鹏等[10]在此基础上,引入模糊系统对迭代滑模参数进行优化,设计模糊自适应非线性迭代滑模控制器,增强参数在不同海况环境下的自适应性,实现更好的风帆助航船舶航向控制;Li等[11]采用RBF神经网络逼近系统的不确定因素,构造自适应RBF神经网络控制器,实现船舶轨迹跟踪;王昊等[12]将动态面技术引入单隐层(Single hidden layer,SHL)神经网络进行控制律设计,简化控制算法,实现协同路径跟踪;Wang等[13]采用模糊系统逼近系统不确定部分,引入Nussbaum函数解决控制方向不确定的问题,结合动态面技术,实现领导者–跟随者的输出同步.

然而,常规动态面基于线性增益设置,使得当系统误差较大时,需要较大的控制量以保证控制精度,然而过大的控制量容易引起系统输入饱和限制;当系统误差较小时,影响控制精度.采用“小误差大增益,大误差小增益”的非线性函数可解决上述矛盾,但无法得到系统稳定.且常规动态面采用的低通滤波器具有一定的延迟,各子系统跟踪误差并不能代表真实的跟踪误差,神经网络本身也会使系统稳定性变差,加剧基于子系统跟踪误差依次反推的不利性.为此采用递归滑模面考虑各子系统误差间的相互关系,恰好也能解决引入非线性函数后对系统稳定性证明的问题.孙秀霞等[14]引入一种非线性增益函数,设计含有积分项的递归滑模面考虑各子系统间误差,利用新的李雅普诺夫函数证明稳定性,实现无人机航迹角跟踪.但该方法假设模型参数摄动和外界大气扰动总和的界已知,实际情况下很难实现.刘希等[15]考虑不确定非线性系统,利用神经网络在线逼近系统不确定项,提出一种非线性增益递归滑模动态面自适应控制方法,有效解决系统的跟踪控制问题.但该方法假设神经网络逼近误差界已知,且所设计非线性增益函数为分段函数,构造略显复杂,实际应用具有一定的局限性,且仅针对单输入–单输出严反馈系统进行控制器设计,故该方法不能直接用于多输入–多输出的船舶轨迹跟踪控制问题.

根据以上研究结果,在文献[15]基础上,针对多输入–多输出三自由度全驱动船舶的轨迹跟踪控制问题,当存在模型不确定和未知外部环境扰动时,引入一种新的简单非线性增益函数和递归滑模面,结合神经网络、动态面技术和自适应鲁棒反演控制,设计出一种基于非线性增益递归滑模的船舶轨迹跟踪动态面自适应控制方法.该方法综合考虑船舶位置和速度误差之间关系设计递归滑模面,引入神经网络对船舶模型不确定部分进行逼近,设计带σ-修正泄露项的自适应律[16]对神经网络逼近误差与外界环境扰动总和的界进行估计,并应用一种非线性增益函数构造动态面控制律,选取李雅普诺夫函数可证明该控制律能够保证轨迹跟踪闭环系统内所有信号的一致最终有界性.最后应用一艘供给船进行控制仿真研究,验证所设计控制器的有效性.

1 问题描述

假设船舶左右对称,考虑前进、横漂和艏摇的三自由度轨迹跟踪船舶轨迹跟踪数学模型可表示为

其中,η=[x,y,ψ]T为船舶在大地参考坐标系下的实际位置(x,y)和艏摇角ψ组成的向量;υ=[u,ν,r]T为船舶在附体坐标系下前进速度u、横漂速度ν和艏摇角速度r组成的向量;τ=[τ1,τ2,τ3]T为船舶推进器控制输入前进力τ1、横漂力τ2以及艏摇力矩τ3组成的控制向量;d=[d1,d2,d3]T为船舶在附体坐标系下受风、浪、流等引起的横向干扰力d1、纵向干扰力d2和艏向干扰力矩d3组成的未知外部环境扰动向量;J(ψ)为坐标系转换矩阵,其表达式为

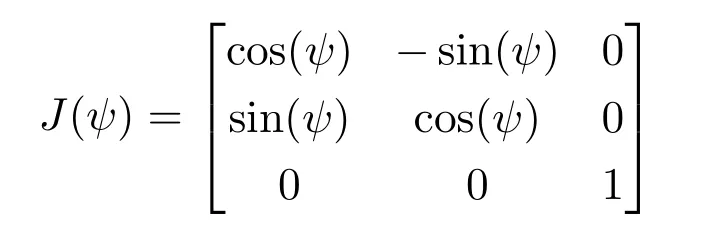
且具备J−1(ψ)=JT(ψ)和kJ(ψ)k的特性;M为船舶重量惯性和水动力附加惯性组成的矩阵;C(υ)为科氏向心矩阵;D为线性水动力阻尼参数矩阵;∆f=[∆f,1,∆f,2,∆f,3]T为船舶模型不确定部分.

假设1.船舶的参考轨迹ηd是光滑可导且有界的,其一阶导数和二阶导数亦是有界的.

假设2.轨迹跟踪船舶数学模型中,船舶重量惯性和水动力附加惯性矩阵M已知且为对角阵、科氏向心矩阵C(υ)和阻尼矩阵D已知;船舶模型不确定部分∆f未知但有界;外部环境扰动d未知但有界.

本文的控制目标是针对船舶轨迹跟踪数学模型(1)和模型(2),在满足假设1和假设2的情况下,考虑船舶存在参数不确定部分且遭受完全未知的有界时变环境扰动,设计控制律τ,使船舶可以沿期望轨迹航行,并保证闭环系统所有信号一致最终有界,实现船舶轨迹跟踪.

2 船舶轨迹跟踪控制器设计

考虑轨迹跟踪船舶存在模型不确定部分和外部环境扰动,引入一种新的简单非线性增益函数和递归滑模面,结合神经网络、动态面技术和自适应鲁棒反演技术,设计非线性增益递归滑模的船舶轨迹跟踪动态面自适应神经网络控制器.

2.1 一种非线性增益函数

为解决常规动态面控制基于线性增益设置使得系统的控制精度与动态品质之间存在矛盾的问题,设计一种非线性增益函数,其表达式为

其中,a>0.该函数具有“小误差大增益,大误差小增益”的优良性质,可有效解决上述矛盾.在常规动态面方法中引入非线性增益函数对李雅普诺夫函数的稳定性证明增加了难度,这在后续采用递归滑模后将得到解决.

性质 1.函数g(x)关于自变量x严格单调递增,为避免x=0时斜率过大的问题,设置其导数

性质2.定义

则对于任意的x,有

成立.

性质3.为避免x=0时除数为零的情况,定义

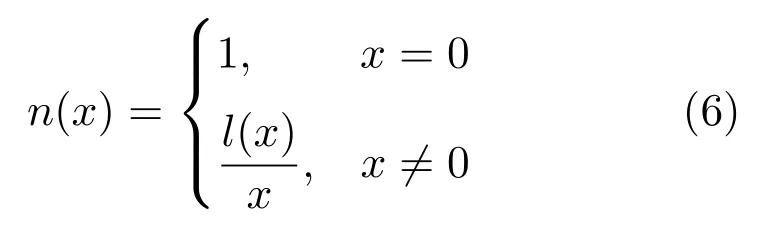
则对于任意的x,有

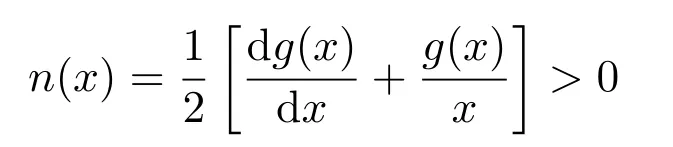
成立.

当a取不同值时,函数l(x)图像如图1所示.

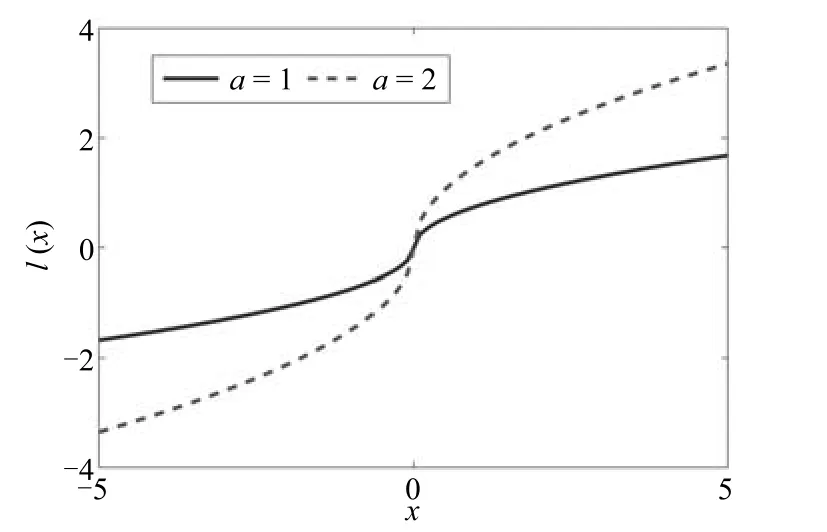
图1 函数l(x)曲线图Fig.1 The curves of functionl(x)

可见,在x较小时,l(x)变化增益较大,而x较大时,l(x)变化增益较小,即“小误差大增益,大误差小增益”.

2.2 控制器设计

步骤1.考虑船舶位置误差向量,定义第一个滑模面向量s1∈R3

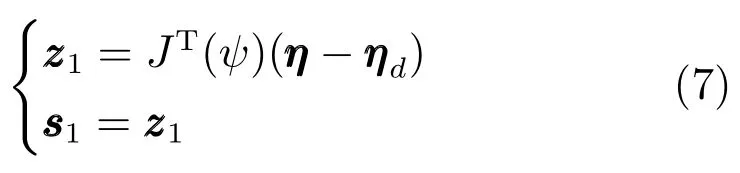
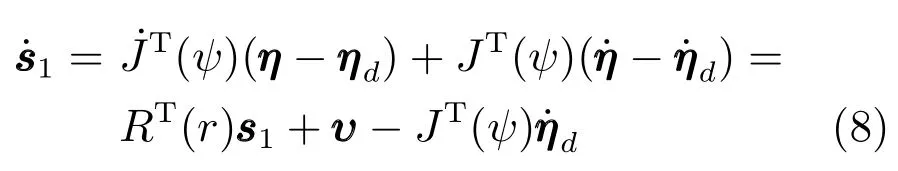
设计υ的虚拟控制向量α1∈R3为

根据Swaroop等[4]提出的动态面方法,引入一个新的状态向量的一阶低通滤波输出,数学表达式为

其中,T为滤波器时间常数.用滤波器的代替项,避免传统反演法中对虚拟控制向量直接求导产生的计算复杂问题,易于工程实现.

步骤2.根据船舶速度误差向量和步骤1得到的位置误差向量,综合考虑两者误差间的相互关系,定义第二个递归滑模面向量为

其中,C1∈R3×3为设计的正定参数对角阵.

考虑到三自由度全驱动轨迹跟踪船舶模型存在参数不确定部分∆f,式(2)是一个三维状态方程组,故引进3个RBF神经网络[17]对其进行逼近.

假设3.对于所有的,神经网络理想权值和逼近误差有界,即存在正的常数和有界函数,使得和成立;再由假设2,则对于轨迹跟踪船舶外部环境扰动d和RBF神经网络逼近误差每一分量来说,存在有界函数δi>0,使,i=1,2,3,即神经网络逼近误差和外部环境扰动d的界向量可表示为.

设计船舶轨迹跟踪状态反馈控制律为

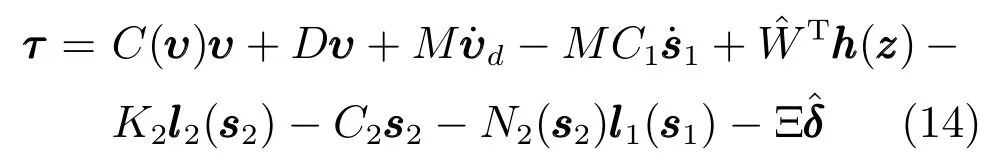
设计权值向量自适应律为

对神经网络逼近误差和外部环境扰动组成的界向量δ,设计其估计值的自适应律为

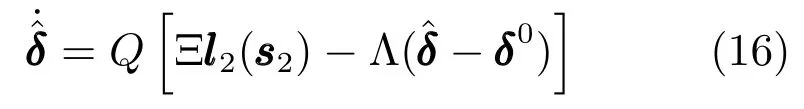
注1.本文为多输入–多输出的船舶轨迹跟踪控制问题,定义代替常规动态面的用以解决稳定性证明的难题;对式(9)引入具有“小误差大增益,大误差小增益”特性的非线性项提高系统控制性能.

注2.在控制律式(14)中,采用具有非线性增益功能的代替,有效改善系统控制精度与动态品质之间的矛盾;递归滑模面项解决常规动态面方法引入非线性增益函数后对李雅普诺夫函数稳定性证明的难题;项用于消除耦合项;双曲正切函数有效消除滑模抖振现象.

注3.神经网络权值的自适应律式(15)和对神经网络逼近误差及外部环境扰动的界的自适应律式(16)中,引入递归滑模函数s2的非线性增益函数,有效防止神经网络及自适应的过度学习,提高系统稳定性.

注4.在设计状态反馈控制器的过程中,文献[15]没有考虑外界环境扰动,用神经网络逼近系统的不确定性;且假设逼近误差界已知,用逼近误差的界构造鲁棒项对逼近误差进行补偿.考虑实际作业船舶不可避免地遭受未知外界环境扰动,且假设逼近误差界已知的情况不容易满足,本文在设计船舶轨迹跟踪控制器的过程中,用神经网络逼近模型不确定部分,逼近误差和外界环境扰动采用基于σ-修正泄露项的自适应律对其界进行估计补偿,提高船舶轨迹跟踪精确性,增强鲁棒性.

2.3 稳定性分析

选择系统李雅普诺夫函数为

对式(17)两边关于时间求导,可得

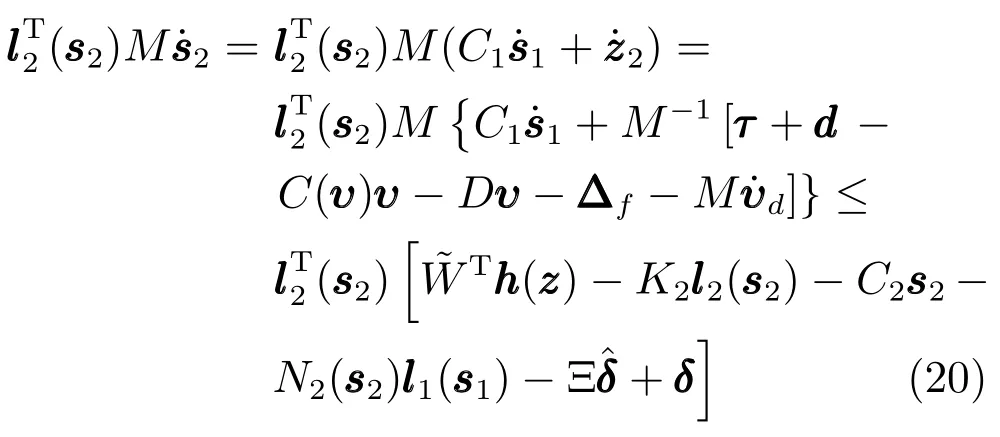
根据以上论述,考虑式(15)和式(16),则式(18)变为

考虑不等式

及不等式

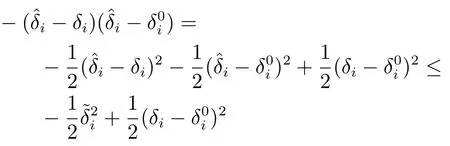
其中,i=1,2,3;且根据双曲正切函数的性质,对于ε>0,a∈R,有 0≤|a|−atanh(a/ε)≤0.2785ε,故

根据非线性增益函数的性质,有如下不等式:

其中,a1为正常数,i=1,2.

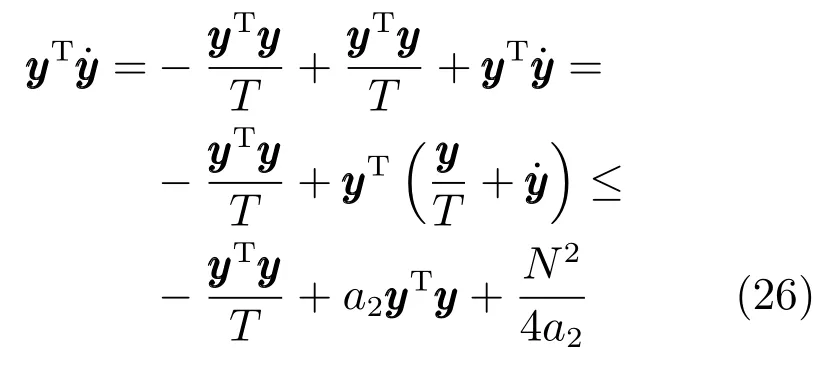
其中,a2为正常数.

按照上述分析,总结定理如下:

定理1.针对三自由度轨迹跟踪船舶的非线性运动学和动力学方程,考虑船舶存在模型不确定部分且遭受未知外部环境扰动,在假设1～3成立的情况下,构造一种新型非线性增益函数式(3),引入神经网络对系统未知不确定部分进行逼近,设计神经网络权值向量自适应律式(15),采用σ-修正泄露项的自适应律式(16)对神经网络逼近误差和外界环境扰动的界进行估计,最终在非线性递归动态面自适应鲁棒控制律式(14)的作用下,得到闭环系统所有信号的一致最终有界性.适当对设计参数K1,K2,和滤波器时间常数T进行调整选择,可以使船舶实现高精度的轨迹跟踪.

证明.解不等式(27),可得

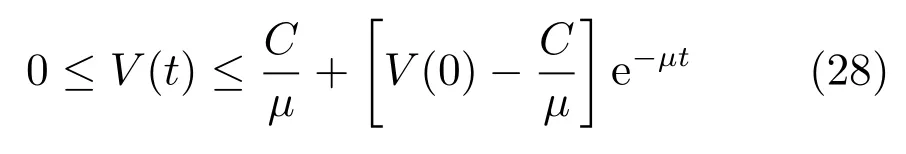
故可知,V(t)一致最终有界;再由式(17)可得系统中的信号一致最终有界;从而由式(7),(9)及(11)可知有界;由和s1的有界性可知η是有界的;由和δ的有界性可知也是有界的.从而得到船舶轨迹跟踪闭环系统内所有信号的一致最终有界性.

3 仿真研究

为验证所设计控制律的有效性,以文献[18]中一艘供给船作为仿真对象进行仿真试验.此船长度为76.2m,质量为4.591×106kg,船舶重量惯性和水动力附加惯性组成的矩阵、科氏向心矩阵、线性水动力阻尼参数矩阵分别为

船舶模型不确定部分为

在仿真中,选择船舶航行期望轨迹为

外部环境扰动为

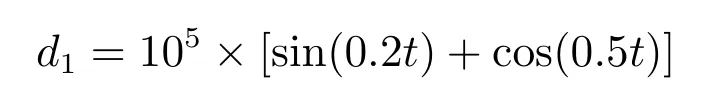
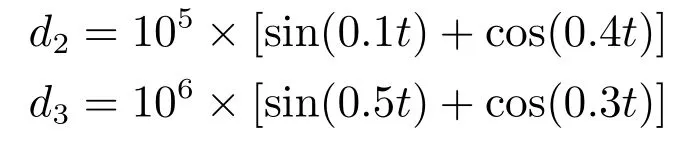
船舶初始位置和速度状态信息为

在相同海况下,采用本文算法与文献[6]基于神经网络的常规动态面算法对船舶轨迹跟踪性能进行仿真比较,系统的初始条件相同,仿真结果如图2∼8所示.

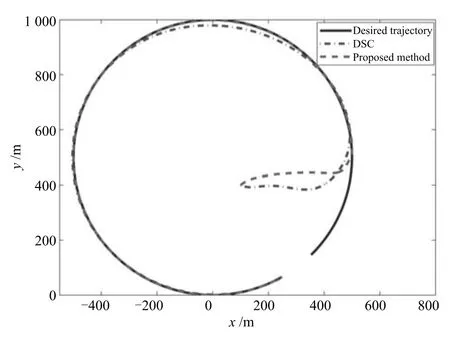
图2 外部环境扰动下船舶的期望轨迹和实际轨迹Fig.2 Desired trajectory and actual trajectory under external environment disturbances

图3 外部环境扰动下期望轨迹η d=[xd,yd,ψd]T和本文算法实际轨迹η =[x,y,ψ]T历时曲线Fig.3Curves of desired trajectoryη d=[xd,yd,ψd]Tand actual trajectoryη =[x,y,ψ]Twith proposed controller versus time under external environment disturbances

图4 外部环境扰动下前进速度u、横移速度ν和艏摇角速度r历时曲线Fig.4 Curves of surge velocityu,sway velocityνand yaw raterversus time under external environment disturbances

图5 神经网络逼近历时曲线Fig.5 Curves of learning behavior of neural networks

图6 控制器输出Fig.6 Curves of controller outputs

图2是相同海况下,大地参考坐标系内船舶的期望轨迹和本文设计控制律及常规动态面设计控制律驱动船舶航行的实际轨迹,表明在模型不确定和未知外部环境扰动存在的情况下,本文设计控制律相较于常规动态面而言,能够较快地跟踪上期望轨迹,且跟踪精度较高;图3是大地参考坐标系下船舶的期望位置、期望艏摇角和本文设计控制律驱动船舶航行的实际位置、实际艏摇角的历时曲线,表明船舶在大约50s左右即能大概跟踪上期望轨迹;图4是前进速度u、横漂速度ν和艏摇角速度r的历时曲线;图5是系统不确定部分∆f,1,∆f,2,∆f,3及RBF神经网络的逼近值NN1,NN2,NN3的历时曲线,表明在50s以后神经网络基本跟踪上所要逼近的不确定项;图6是本文设计控制器输出,可以看出控制律光滑合理;图7是外部环境扰动和逼近误差的界δ1,δ2,δ3及其估计值历时曲线,且放大从20s到300s的跟踪曲线,可以看出所设计修正泄漏项的自适应律参数选取合适,能够对外部环境扰动和逼近误差的界进行估计;结合图5神经网络逼近效果,可以看出在神经网络跟踪有误差的情况下,自适应律也能够进行很好的估计从而保证船舶的高精度航行;图8是相同海况下本文算法与常规动态面算法跟踪性能比较,其中表示位置误差范数,可以看出,本文算法跟踪性能较常规动态面虽然前30s稍慢,但30s后明显优于常规动态面,跟踪误差衰减快;且基于“小误差大增益,大误差小增益”的本文算法考虑递归滑模在一定程度上削弱神经网络造成的误差,45s后基本跟踪上期望轨迹,稳态误差小,总体上性能优于常规动态面.

4 结论

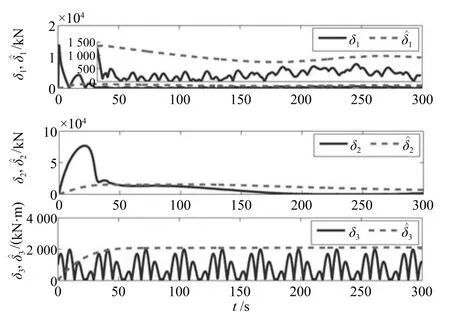
图7 外部环境扰动和逼近误差的界δ1,δ2,δ3及其估计值ˆδ1,ˆδ2,ˆδ3历时曲线Fig.7 Curves of the bounds of external environment disturbances and approximation errorsδ1,δ2,δ3and their estimationsˆδ1,ˆδ2,ˆδ3verse time with proposed controller

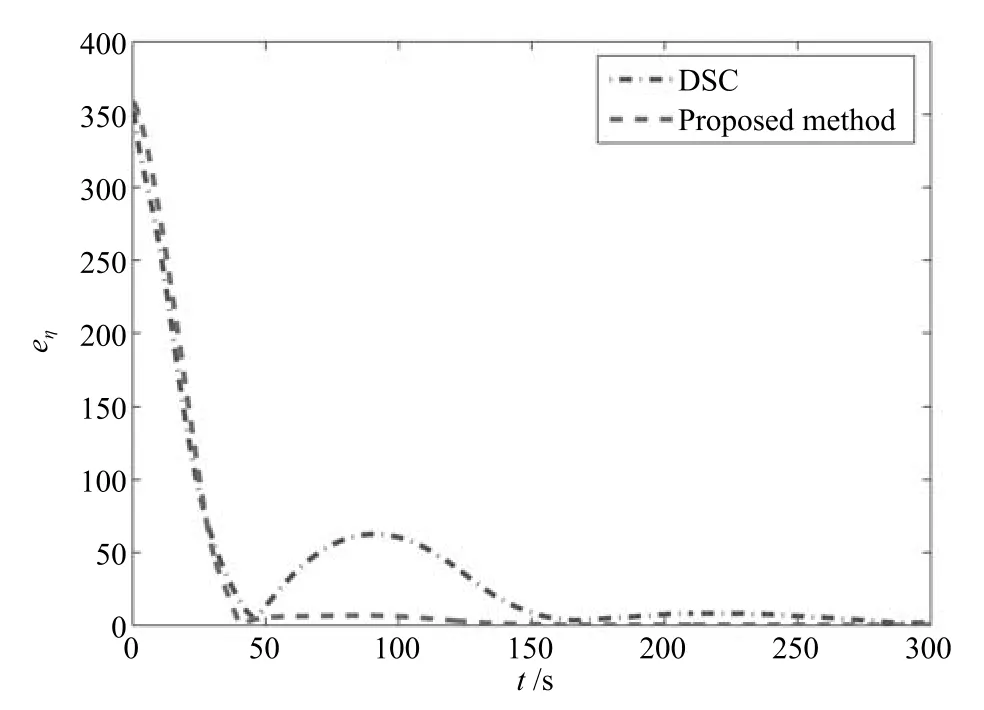
图8 相同海况下本文算法与常规动态面算法跟踪性能比较Fig.8 Comparison of tracking errors under the same sea conditions between the proposed method and the dynamic surface control method

考虑三自由度全驱动船舶具有模型不确定部分且遭受未知外部环境扰动,引入非线性增益函数和递归滑模面,结合神经网络、动态面技术和自适应鲁棒反演控制,设计出一种基于非线性增益递归滑模的船舶轨迹跟踪动态面自适应控制器.非线性函数的引入和递归滑模面的设计,能有效解决常规动态面方法对低通滤波器时间常数和神经网络自适应参数摄动脆弱的缺点.基于李雅普诺夫函数证明了该控制律可实现船舶的高精度轨迹跟踪,并保证系统内所有信号的一致最终有界性.最后以一艘供给船舶进行仿真试验,验证了所设计控制器的有效性,仿真结果表明,采用非线性增益递归滑模的船舶轨迹跟踪动态面自适应控制方法,可提高船舶轨迹跟踪速度和控制精度,且控制力和力矩光滑合理,更加符合船舶的实际操作要求,在工程实际中具有一定参考价值.