基于自适应最优Morlet小波的滚动轴承故障诊断*

祝小彦， 王永杰， 张钰淇， 袁婧怡

(华北电力大学能源动力与机械工程学院 保定，071003)

引 言

滚动轴承在机械设备中是最常用和最重要的零件之一，其运行状态直接影响到整台机器的性能，机械设备发生故障很多都是由滚动轴承故障所引起的，所以滚动轴承的故障诊断具有很重要的意义[1]。滚动轴承故障发生早期，传感器采集到的振动信号中的冲击成分比较微弱，常常淹没在强背景噪声中，这给滚动轴承的故障诊断造成了很大的困难。因此，滚动轴承早期故障的诊断一直是滚动轴承故障诊断研究的重点和难点。

由于小波分析在冲击振动信号处理上具有其他方法不具备的优势，滚动轴承的故障诊断中小波分析方法一直以来备受关注。在滚动轴承的故障诊断中尤其是滚动轴承的早期故障诊断，要求小波分析方法具有更加细腻的时间尺度网格划分能力以及与冲击成分更加匹配的基小波，离散小波在这些方面优势并不明显，并且由于离散小波在尺度上是离散的，在故障检测过程中漏检和判断失误时有发生，而连续小波分析方法则可以弥补这些方面的不足，Morlet小波就是其中的典型代表。

Morlet小波的时域波形与冲击衰减的波形十分相似，表现为其幅值由小波中心向两边振荡衰减直至为零的特征，而滚动轴承故障信号中的冲击成分通常也呈现出一种冲击衰减的特征，这种波形上的相似性使得Morlet小波比较适合于滚动轴承的故障诊断。通过调整相关参数得到最优Morlet基小波，就可以实现Morlet小波对故障冲击成分的最佳匹配。目前相关文献虽然也提到最优Morlet小波的概念，但是实际上并不能真正实现最优Morlet小波，而是一种相对最优Morlet小波。文献[2]采用Morlet小波与奇异值分解相结合的方法实现了对机械测试信号的有效消噪，但是文章并没有对其参数进行优化，因此难以保证结果的稳定性。文献[3]提出了以Shannon熵为评价标准，对Morlet小波的带宽参数fb进行了优化，提取了信号中冲击成分，但其并没有对中心频率fc进行优化。文献[4]虽然兼顾了带宽参数fb和中心频率fc，但其并没有同时考虑小波尺度a对信号分析的影响，这样做忽略了三者之间的相互关系，得到的Morlet小波并不一定是最优的。

基于粒子群优化算法在多参数优化中的优异表现, 笔者提出了自适应最优Morlet小波分析方法，并将其应用到滚动轴承早期故障诊断中。仿真数据试验与实测数据试验对比结果表明了本方法具有一定的有效性和优越性。

1 自适应最优Morlet小波

1.1 Morlet小波

给定一维振动信号x(t),对其进行Morlet小波变换可以得到

(1)

其中:W(a,b)为Morlet小波变换系数;a为连续小波的尺度参数;b为移位参数;φ(·)是以Morlet小波为母小波的小波基；“*”表示共轭。

在信号处理过程中，上述计算方法较为复杂、耗时，并不能满足实际要求。根据Parseval定理[5]，可以得到一种更为简单快速的计算形式

(2)

其中：ψ(af)=e-π2f b(af-fc)2，FT和IFT分别代表傅里叶变换及其逆变换；fc为Morlet母小波的中心频率；fb为Morlet母小波的带宽参数；a为Morlet小波变换的尺度参数。

由式(2)可知，只要对原始信号x(t)和Morlet母小波φ(t)的傅里叶变换进行相应的FT处理，最后经过傅里叶逆变换就可以快速实现人们需要的Morlet小波变换的结果。

1.2 自适应参数优化

从上述分析中可以看出，Morlet小波分析过程中有3个参数会对分析结果产生决定性的影响：尺度参数a、带宽参数fb和中心频率fc。从式(2)中可以看出，尺度参数a直接影响着Morlet小波滤波的频带范围，太大或太小的尺度参数都不能将故障信号准确地分解到相应的频带中；Morlet母小波带宽参数fb决定了Morlet小波振荡波形衰减的快慢，Morlet母小波中心频率fc决定了Morlet小波波形的振荡频率，fc与fb同时影响着母小波与故障冲击成分的匹配程度。可见尺度参数a、带宽参数fb和中心频率fc对Morlet小波的滤波效果影响较大，有必要对其取值进行优化。

值得注意的是，尺度参数a、中心频率fc和带宽参数fb三者在Morlet小波分析过程中并不是完全独立的，如果单独优化其中一个或两个参数并不能获得最优的Morlet小波分析结果。

粒子群优化算法是一种基于迭代模式，能够在适应度值的约束下并行实现多个目标参数优化的优化方法。假设粒子的种群规模为Q，搜索空间的维数为D，则第i个粒子位置表示为xi=(xi,1,xi,2…xi,D)，粒子i速度表示为vi=(vi,1,vi,2…,vi,D),其中i=1,2,…,Q。标记第i个粒子搜索到的最优位置为pi=(pi,1,pi,2,…,pi,D)，种群中搜索到的最优粒子位置标记为pz=(pz,1,pz,2,…,pz,D)。迭代过程中每个粒子的位置和速度按照下式更新

其中:ω为惯性权重;c1，c2称为学习因子;r1，r2为介于[0,1]之间的随机数;i=1,2,…,Q;d=1,2,…,D。

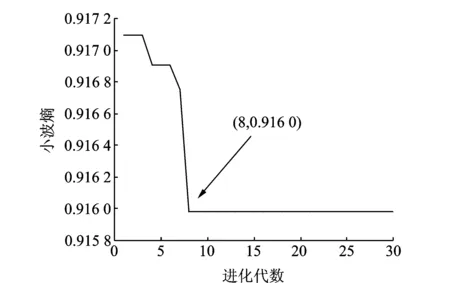
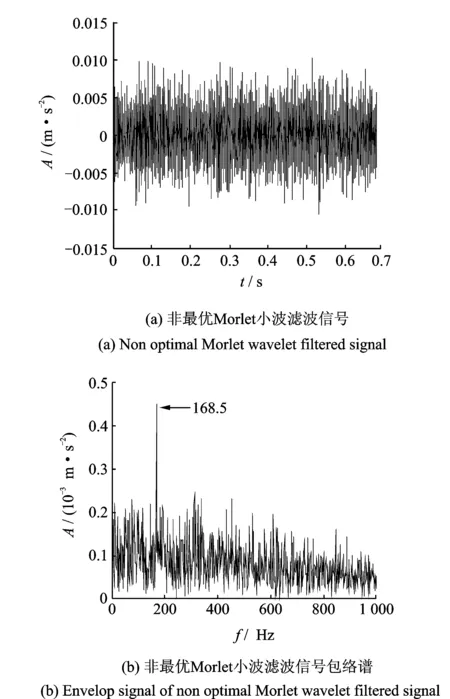
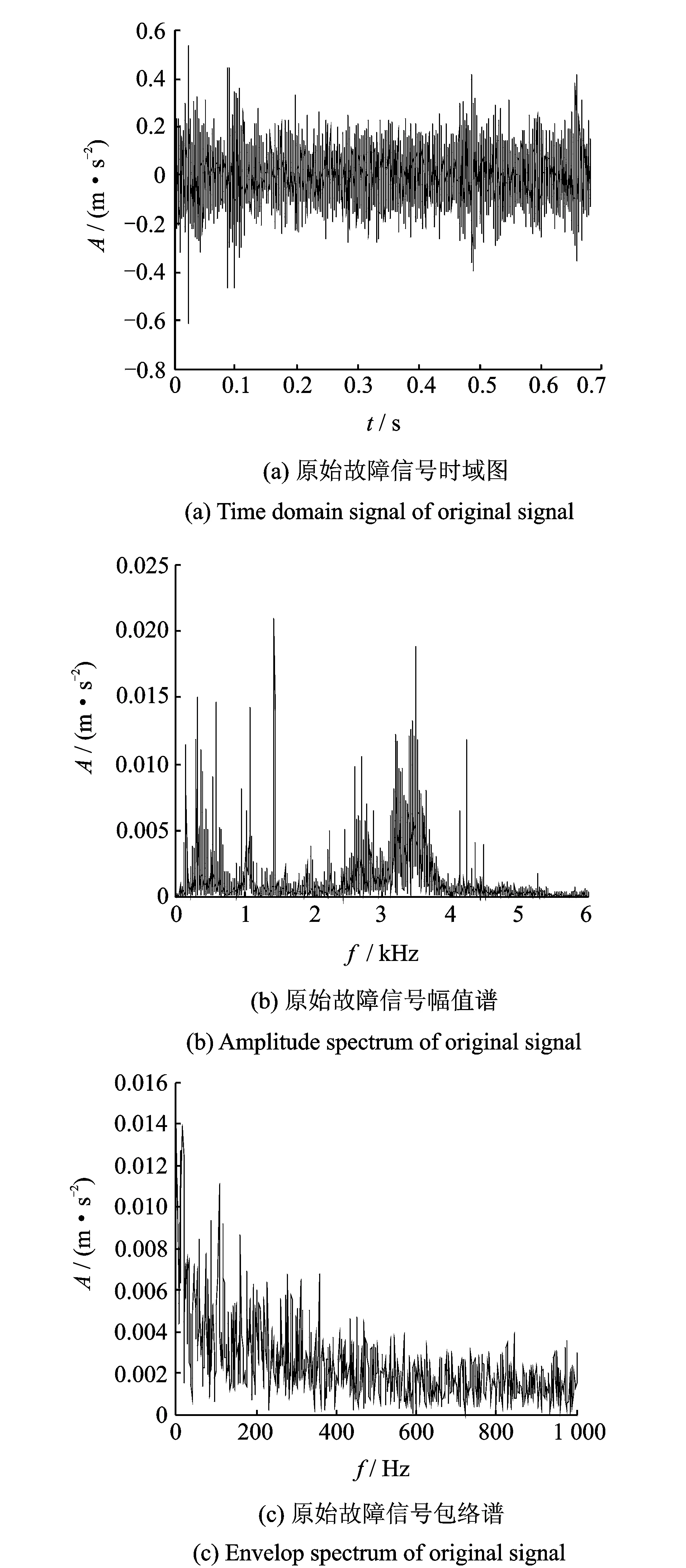
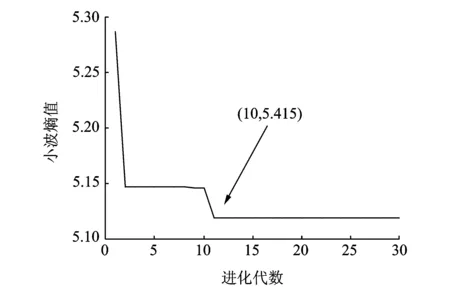
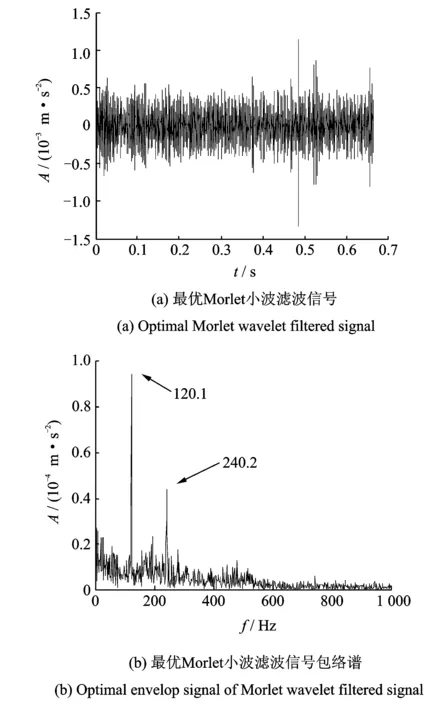
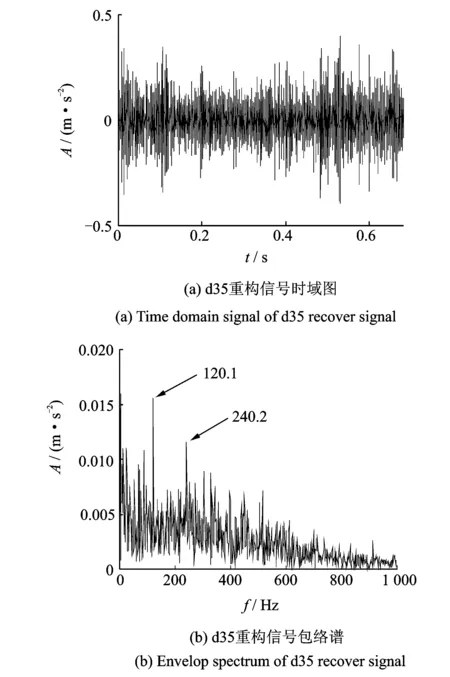
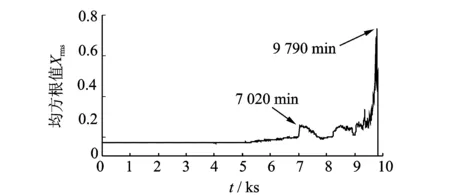
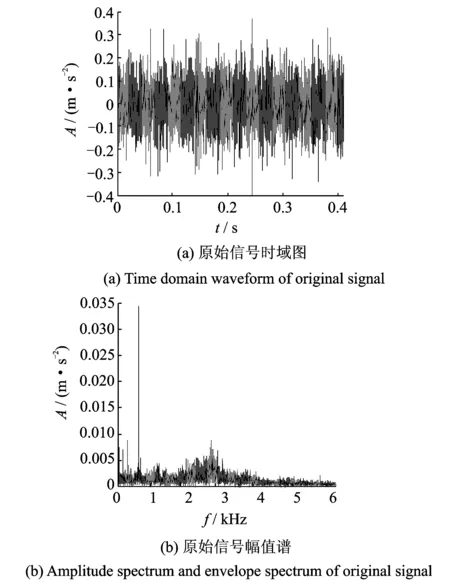
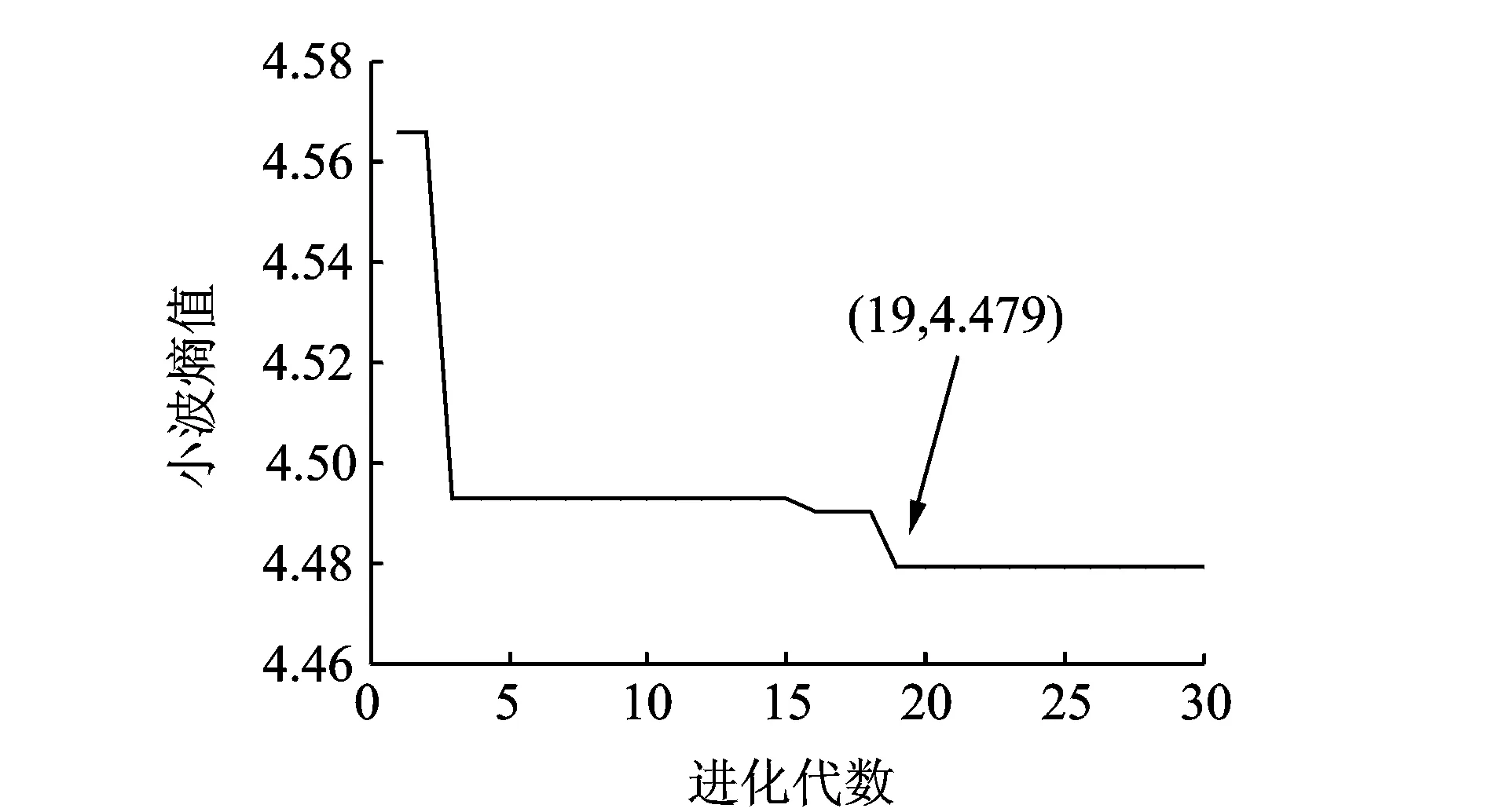
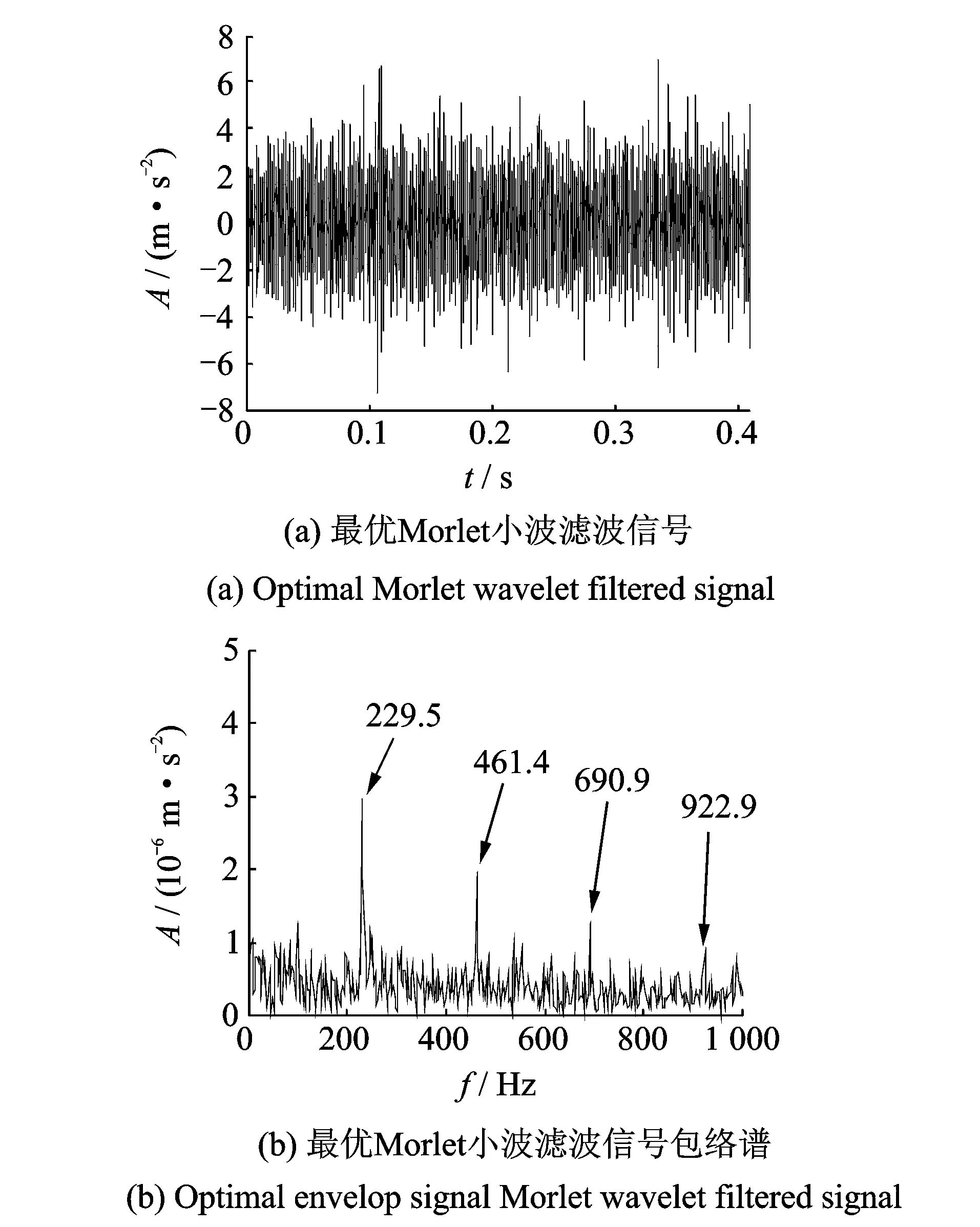
粒子群优化算法的粒子位置选取的约束较弱，为保证粒子位置在约束范围内取值，通常情况下对种群中粒子位置和速度进行相应的约束，即当vi,d>vmax时，令vi,d=vmax；而当vi,d

为实现Morlet小波最优参数的选取，文中采用粒子群优化算法对3个核心参数同时寻优，保证了3个参数之间的相互关系不会被破坏，从而真正实现自适应最优Morlet小波分析。

1.3 适应度值的选择

粒子群优化算法的迭代过程中，每次迭代都要对当前最优Morlet小波进行评价，并判断其是否为最优解。因此，适应度值的选择较为关键。目前，峭度最大原则[6]和最小熵原则[7]是应用较为广泛的评价准则。峭度是一种四阶累积量，对信号中的突变成分十分敏感。然而研究(如图1所示，其中(a)信号中峭度值为2.990 7，熵值为0.918 95；(b)信号中峭度值为7.013 7，熵值为0.835 95；(c)信号的峭度值为13.834 7，熵值为0.902 53)发现，当信号中总体幅值较平缓但存在幅值较大的孤立冲击成分时，其峭度值往往会比较大。但该冲击成分有可能是由于轴承故障外的原因产生的，原故障信号本身并不一定具有较强的稀疏性(图1(b,c)具有近似的峭度值，但显然原始冲击信号的稀疏性明显要比含有冲击成分故障信号的稀疏性强)。因此,利用峭度值作为适应度值很有可能造成误诊；与之相比，熵则能够较稳定地描述信号的稀疏程度，即使信号中出现了孤立存在的冲击成分，其熵值也不会出现剧烈变化。

根据最小熵原理，信号稀疏性越强，熵的值越小，对应的Morlet基小波与冲击成分的匹配程度越高。通过比较熵值的大小就可以判断Morlet基小波与信号中的冲击成分的匹配程度，从而找到最优Morlet基小波。因此，本研究选择Shannon小波熵作为粒子群优化算法的适应度值。

2 本方法简介

Morlet小波是高斯包络下的复指数函数，具有很好的时频域局部化性能，其带通滤波特性不仅可以实现对故障信号的有效滤波，而且能够对故障信号中的有效成分进行准确识别和提取。然而，Morlet小波处理效果严重依赖于参数的设置。当基小波与信号冲击成分相匹配时，故障特征提取比较准确；当基小波特性与冲击成分相差较大时，Morlet小波将难以实现对故障特征的识别。同时，即使找到了最优Morlet母小波但没有匹配的最优尺度参数a，其分析结果也不会很理想。因此，获取最优Morlet母小波和最优尺度参数a是正确利用Morlet小波进行滚动轴承故障诊断的前提。

文中利用粒子群优化算法在获取最优Morlet母小波，保证Morlet小波分析具有最优的带通滤波特性的同时，实现了对Morlet小波3个核心参数的自适应最优选择，解决了靠经验确定小波参数的盲目性和低效率的问题，试验结果取得了良好的效果。文中所提方法具体实现过程如下：

1) 设定粒子群优化算法的惯性权重ω=1，并取学习因子c1=c2=2，种群规模设为100，进化次数为30；

2) 利用带宽参数fb和中心频率fc构建粒子位置x=(fb,fc)，并取Shannon小波熵作为粒子群优化算法的适应度值，同时指定尺度参数a的取值范围[amin,amax]，通常设定为[0.1,1]，步长取0.1；

3) 将新粒子位置带入Morlet小波变换中，并在[amin,amax]尺度范围内得到分解结果，找到最小Shannon小波熵和取得最小Shannon小波熵时对应的尺度参数abest；

4) 通过不断迭代变换更新粒子位置，最终获得粒子的最优位置xbest=(fb,best,fc,best)以及对应的最优尺度参数abest。将最优参数带入Morlet小波变换中，对故障信号中的冲击成分进行准确提取，实现对信号的滤波降噪；

5) 对最佳滤波信号作包络谱，提取故障信号中的特征频率成分，并通过谱图中的主导频率与滚动轴承各元件的故障特征频率作对比判断轴承的故障类型。

3 仿真试验

利用滚动轴承故障模型[8-10]对内圈故障时产生的冲击信号进行模拟，并添加强烈白噪声模拟轴承内圈早期故障信号。仿真信号为

(5)

其中：s(t)为周期性冲击成分；n(t)为高斯白噪声；幅值A0为0.5；τi为第i次冲击相对于周期T的微小波动；衰减系数C为800；共振频率fn为4 kHz；转频fr为20 Hz，内圈故障特征频率fi=1/T=170 Hz，随机波动服从零均值正态分布；标准差为转频的0.5%；仿真信号信噪比为-13 dB，采样频率fs为12 kHz；采样点数N为8 192。

仿真信号时域波形如图2所示。可以看到时域图中周期性的冲击成分被信号中强噪声所掩盖，难以观察到故障信息，仿真信号幅值谱及其包络谱中干扰频率较多也难以观察到较为突出的频率成分。

图2 仿真信号时域信号、幅值谱及其包络谱Fig.2 Time domain waveform, amplitude spectrum and envelop spectrum of simulation signal

图3 小波熵进化曲线Fig.3 Wavelet entropy evolution curve

图4 最优Morlet小波滤波信号及其包络谱Fig.4 Optimal Morlet wavelet filtered signal and its envelop signal

利用所提方法对仿真信号进行分析。设定带宽参数fb的寻优范围为[0,200]，中心频率fc的寻优范围为[0,100]，尺度参数a的匹配范围为[0.1,0.2]，步长为0.01，进化次数设定为30次。最终确定带宽参数fb、中心频率fc最优参数组合为[105.118 7 ,32.670 5] ，最优尺度参数a为0.7。图3表示小波熵随随进化代数变化的寻优曲线，可知小波熵最小值0.916出现在第8代。由此设定Morlet小波变换参数分析仿真信号，从而得到Morlet小波滤波的最优结果，如图4所示。由图4(a)所示，最优Morlet小波滤波信号与原仿真信号相比冲击成分明显增多。图4(b)中对滤波信号作包络分析，可以清楚看到内圈故障频率的基频(168.5 Hz)、2倍频(338.4 Hz)、3倍频(506.8 Hz)。据以上分析，可以判断仿真信号的内圈已经发生了故障。

为证明本方法的准确性，图5中只对最优参数组合中的带宽参数值进行修改(新参数组合为[50, 32.6705 , 0.7])，并利用新的参数组合对仿真信号进行Morlet小波分析，图5(b)中只出现了内圈故障频率的基频成分。

图5 非最优Morlet小波滤波信号及其包络谱Fig.5 Non optimal Morlet wavelet filtered signal and its envelop signal

由以上仿真信号试验结果可以看出：由于滚动轴承故障早期信号中的背景噪声较强，轴承故障点冲击产生的冲击成分又比较微弱， 因此，信号时域图、幅值谱及其包络谱中都难以发现与故障相关的信息，诊断失效。利用笔者所提方法，通过粒子群优化算法求取Morlet小波的最优参数组合，并将其带入Morlet小波中对仿真信号进行有效滤波，可以有效提高信号中的信噪比、突出冲击成分，在其包络谱中成功找到了多个与故障相关的故障频率成分，判断出轴承故障，证明了笔者所提方法的有效性。通过更改参数的试验证明了本方法具有良好的准确性。

4 实测信号试验

4.1 人工植入故障试验

实验数据采用美国凯斯西储大学电气工程实验室滚动轴承滚动体故障信号。实验中所用驱动端滚动轴承为SKF 6203，具体参数如表1所示。采用电火花技术在轴承上加工单点凹痕模拟早期故障，人为加工的轴承损伤直径分为0.177 8，0.355 6和0.533 4 mm，为体现所提方法的有效性，选用故障程度最轻的0.177 8 mm。传感器采样频率为12 kHz，电动机转速为1 797 r/min。滚动体扰动频率为3.987 4 Hz，计算可知滚动体故障特征频率fb为119.4 Hz。电动机转频fr为29.95 Hz。

表1 SKF 6203轴承结构参数

图6 原始故障信号时域波形、幅值谱及其包络谱Fig.6 Time domain signal and Amplitude spectrum and Envelop spectrum of original signal

原始故障信号的时域波形如图6(a)所示。可以看出信号中的故障特征较为微弱，难以觉察到轴承故障的迹象。图6(b)幅值谱中虽然有较多的共振谱线，但并没有发现与故障相关的频率谱线出现。

对原始故障信号作进一步包络分析如图6(c)所示。可以看出由于故障特征较为微弱，包络图中频率谱线十分杂乱仍然难以找到与滚动轴承故障相关的频率成分，诊断失效。

利用笔者所提方法对该数据进行自适应最优Morlet小波分析。首先设定带宽系数fb寻优范围为[0,200]，中心频率fc寻优范围为[0,100]，并且设置尺度参数a的匹配范围为[0.1,0.3],步长为0.01。然后利用粒子群算法对Morlet小波参数进行优化。图7中，小波熵在第10代取得最小值5.145。最优Morlet 小波参数对为[96.781 5, 32.190 8]，对应的最优尺度参数a的值为0.16。

图7 小波熵进化曲线Fig.7 Wavelet entropy evolution curve

从图8(a)中可以看出，最优Morlet小波滤波信号中冲击成分与原信号相比更加明显突出。对其作进一步包络分析，图8(b)中可以清楚地看到滚动体故障特征频率的基频成分(120.1 Hz)及其2倍频(240.2 Hz)。由此可以做出准确判断：滚动轴承滚动体发生故障。

图8 最优Morlet小波滤波信号及其包络谱Fig.8 Optimal Morlet wavelet filtered signal and its envelop signal

图9 d35重构信号时域图及其包络谱Fig.9 Time domain signal and envelop spectrum of d35 recover signal

图10 试验台示意图Fig.10 Schematic diagram of experiment platform

为证明本方法的优越性，对故障信号进行小波包分解，小波基函数选择db10。经过信号分解、重构并对重构信号进行包络分析发现，节点(3,5)处信号的包络图中故障特征频率最明显，如图9所示。图9(a)为d35重构信号，其周期性特征并不明显。图9(b)重构信号包络谱中虽然能够找到与滚动体故障特征频率相关的基频及其2倍频，但是图中干扰谱线较多，噪声并没有得到较好的抑制。由此可见所提方法的处理效果更佳。

4.2 全寿命故障周期试验

试验分析数据来自NSFI/UCR智能维护系统中心的滚动轴承全寿命周期加速度试验[11-12]，试验台布局如图10所示。试验台转轴上安装有4个型号为ZA2115滚动轴承，其结构参数如表2所示。并利用弹性系统在轴承和转轴上加载约2 671 N的径向载荷，转轴转速为2 000 r/min。滚动轴承轴向和径向分别安装有353B33型高灵敏度ICP加速度传感器。试验过程中共进行3组试验，利用NI DAQCard-6062采集卡采集试验振动信号，采样频率为20 kHz。其中第2组试验持续时间为164 h，共采集数据文件984个，采样间隔为10 min，采样点数为20 480。文中数据选用第2组试验数据对一号滚动轴承外圈故障进行分析。经计算，轴承外圈故障特征频率fo为236.4 Hz。

如图11所示，试验轴承在0～9 790 min全寿命周期内，表征轴承故障程度的均方根值发生了显著的变化。约5 100 min之后轴承故障开始有所增加，但波动幅度并不大，这一阶段一般称之为轴承故障的早期阶段；而在7 020 min轴承振动信号的均方根值发生了突变，轴承故障进一步加剧，直到试验最后均方根值达到最大轴承失效。试验结束后在轴承外圈上发现了明显的剥蚀现象。

表2 ZA2115滚动轴承结构参数

图11 轴承故障发展趋势图Fig.11 Bearing fault tendency chart

图12 原始信号的时域图、幅值谱及其包络谱Fig.12 Time domain waveform，amplitude spectrum and envelope spectrum of original signal

为了验证本方法对滚动轴承早期故障的有效性，文中选择5 310 min时故障刚开始发生时的试验数据进行分析。图12(a)振动信号的时域波形中虽然出现了较多的冲击成分，但是其规律性并不明显。图12(b)频谱图主导频率成分中也难以发现与滚动轴承故障相关的频率成分。图12(c)中对故障信号进行包络谱分析。可以看出，包络谱分析也难以提取出故障相关的频率成分，诊断失效。

利用笔者所提方法对振动信号进行分析，如图13所示。设定带宽系数fb寻优范围为[0,200]，中心频率fc寻优范围为[0,100]，并且设置尺度参数a的匹配范围为[0.1,0.3],步长为0.01。利用粒子群算法对Morlet小波分析参数优化。图13中小波熵在第19代取得最小值4.479。最优Morlet小波参数组合为[96.781 5, 32.190 8]，对应的最优尺度参数a的值为0.16。

图13 小波熵进化曲线Fig.13 Wavelet entropy evolution curve

利用最优Morlet小波对故障信号进行分析， 最优Morlet小波滤波信号时域波形如图14(a)所示。从图中可以看出，与原始信号相比最优Morlet小波滤波信号中的冲击成分更加突出，可以明显看出其具有一定的规律性。图14(b)中对故障信号作进一步包络分析，图中出现了4条与轴承外圈故障有关的故障频率成分，由此可以断定滚动轴承的外圈发生了故障。

对故障信号进行小波包分解，小波基函数选择db10。经过信号分解、重构并对重构信号进行包络分析发现，节点(3,2)处信号的包络图中故障特征频率最明显，如图15所示。

图14 最优Morlet小波滤波信号及其包络谱Fig.14 Optimal Morlet wavelet filtered signal and its envelop signal

图15 d32重构信号时域图及其包络谱Fig.15 Time domain signal and envelop spectrum of d32 recover signal

从图15(b)d32重构信号包络谱中仅可以找到外圈故障特征频率的基频和2倍频，但小波包分解并没有对信号中的噪声成分起到很好的抑制作用，干扰成分较多，因此所提方法处理效果更加准确。

5 结束语

滚动轴承早期故障信号中冲击成分十分微弱并受强背景噪声的影响使得常用的频谱分析和包络分析方法难以直接得出准确的诊断结论。 与离散小波相比，Morlet 小波具有更加细腻的时间尺度网格划分能力，在处理滚动轴承早期故障信号时能够更加准确的提取信号中的故障信息，更加适合处理轴承早期故障信号。Morlet小波能够有效提取振动信号中的冲击成分，抑制信号中的背景噪声，使得其十分适合对滚动轴承早期故障的诊断。借助于粒子群优化算法不仅能够使得处理结果达到最优，而且能够实现Morlet小波分析参数的自适应选取，解决了靠经验确定小波参数的盲目性和低效率的问题。试验结果证明,笔者所提方法具有一定的有效性和准确性。