基于CAD模型的船舶有限元建模方法
2018-11-01,,,
, , ,
(1.华中科技大学 材料科学与工程学院,武汉 430074;2.中国船级社 技术研发中心,北京 100007)
目前船舶有限元模型的快速生成技术不是很成熟,第一,大部分只能通过手工的方式从二维图纸上量取尺寸,然后输入到Patran、Ansys等有限元软件中,建模过程比较复杂,影响了建模的效率。第二,船体结构中包含了复杂的曲面曲线,各板架属于独立结构,在拓扑上没有连接,在实际网格划分时各个板架只能被独立网格化,不同网格之间难以相互匹配,从而限制了船舶有限元建模技术的进一步发展[1]。
船舶有限元技术向着CAD/CAE 集成方向发展,而目前大部分的CAD/CAE集成系统采用一种中间标准数据格式文件,例如,GES/VDA/STEP/DXF等,将CAD模型导出,然后再导入到CAE系统中生成几何,简化、生成有限元网格[2]。这种方式会造成CAD建模的参数化特征丢失和信息丢失,产生大量的冗余,CAD模型的修改面临重复转换、几何修补和拓扑重建等问题[3]。
针对CAD/CAE集成技术的研究,已涉及从CAD到分析模型的创建过程,近些年来主要采用调整现有CAD模型以适应分析需求的方法[4-5],但是由于CAD/CAE系统之间的差异性,使得直接在CAD模型上进行修改变得难以实现[6-8]。提出了一种表单特征方法,通过在B-Rep模型上添加附加的信息来适用于网格的生成[9-10],但是这种方式仅支持基于特征建模的环境。至于高级拓扑(HLT)的方法,虽同时支持B-Rep和多面体表示,并在CAD模型和多面体模型之间创建连接,但是为了让高级拓扑适合于网格生成,还是会丢失拓扑变换的操作过程[11-12]。
综上,提出一种CAD/CAE集成系统的有限元网格自动生成技术,一方面使用中间模型实现CAD模型和有限元网格之间的连接,修改CAD模型会自动更新有限元网格,另一方面解决相交板架有限元网格的匹配问题。
1 有限元网格的创建过程
图1是使用通用CAD建模软件建立的船舶外壳模型。由图1可见,整个外壳是由多张曲面拼接而成,在实际划分网格时,不希望网格节点沿着分片缝分布,需要进行面的合并,而在CAD环境下很难将多张曲面合并成一张曲面。
因此,引入一种多面体模型作为中间模型,采用数字化测量的方式得到多面体模型,在误差范围内离散成三角形面片,在多面体模型下实现多张曲面的“焊接”。多面体模型保证了CAD模型与网格之间的关联,可以直接用于网格的生成,提高建模效率。
图2为基于NX平台完成的船舶有限元前处理系统,在建模环境下进行产品建模,然后使用NX的多面体模型生成器将产品模型(B-Rep表示)转换成多面体模型[12],多面体模型减小了产品模型和网格模型之间的差距,可以直接用于网格划分。
2 建立船体相交结构的连接关系
在进行实体建模时,船体的板架结构是以独立的结构进行创建的,在拓扑结构上没有关联,造成在生成有限元网格时,空间各个板架被独立网格化的问题。如图3所示,船舶中存在许多结构与外壳相交,但是并没有“焊接”在一起,导致在网格划分时不能生成相互匹配的网格。
因此,许多软件在进行网格划分之前在CAD模型中实现相交结构的“焊接”,但是CAD模型需要使用B-Rep建模,对于空间上相互靠近的曲线很难实现缝合操作。如图4所示,左图中2个结构在空间上存在2条相互靠近的边,右图是通过移动2条靠近的边来实现缝合,由于CAD中的边由一系列控制点描述,很难实现空间上的挪动,同时改变了CAD模型的空间拓扑。
为此,提出一种新的建模方式,实现相交板架的缝合。如图5所示,在CAD模型中进行几何的切割,并没有实现2个独立结构的“焊接”操作,而是将相互匹配的边存储起来,然后将CAD模型转化成多面体模型,在多面体模型中通过移动多边形节点来实现相交结构的“焊接”。这样既不影响CAD模型,又能实现网格的相互匹配。
2.1 相交板架的分组
在CAD模型中,在切割之前需要按照目标体和切割工具进行分组。
船体模型中几何体数量巨大,1艘散货船模型中的结构数量大约是2 000个,而每块板架的拓扑结构复杂,如果直接通过测量2个几何的距离来判断结构是否相交,效率低下,所以需要使用AABB(axis-aligned bounding box)算法进行筛选[13],然后再进行精确判断。
步骤1:使用曲面的包容盒进行粗筛。首先对整个模型中的所有曲面求取其包容盒,然后使用AABB算法,按照划分的最大层数和空间格中最小曲面数量进行空间的划分,然后再求取曲面几何的最小包容盒。考虑到模型的误差,需要求取的最小包容盒的放量包容盒,对求得的包容盒进行放大,然后在使用AABB算法建立的八叉树数据中查询与其相交的结构,最后在小范围中进一步筛选得到线相交的结构。
步骤2:通过小范围精确的计算得到与曲面相交的曲面(线接触)。
2.2 相交板架在CAD中切割
在CAD环境下使用B-Rep建模方式很难将多个结构合并成一个结构,所以只能进行切割操作,并记下切割信息,利用切割信息在多面体模型中进行缝合。
如图6所示,存在一组相交的板架,sheet2的e6和sheet3的e7是与sheet1相交的边。
步骤1:sheet2对sheet1进行切割。
首先求得sheet2中的e6与sheet1相交,如图7所示,sheet1上生成e10和e11,同时为了生成相互匹配的边,sheet2的e6边被分割成e8和e9。
为了实现2个板架在拓扑上的连接,需要保存匹配边的信息,一次切割生成的匹配边见表1。
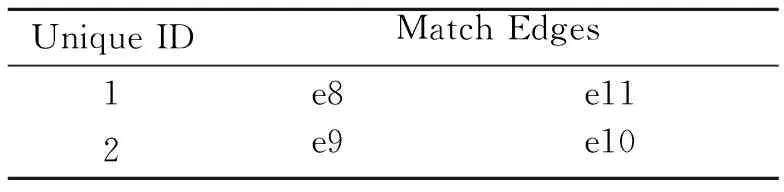
表1 一次切割匹配边生成
注:Unique ID表示使用一个GUID唯一表示一组数据,Match Edges表示相互重合的一组边,Unique ID对应一组Match Edges,如表1中e8和e11为一组匹配边,e9和e10是一组匹配边。
虚拟拓扑的定义和相关的虚拟拓扑操作,可以实现匹配边的合并[14],但是主要用于几何的简化操作,本文在实现中仍然保持CAD模型中几何拓扑关系,只是在模型交于图形系统显示时仅显示列表中的一条边。
步骤2:shee3对sheet1进行切割。如图8所示,首先在一次切割生成的匹配边的列表中查询,发现已存在e10和e11与sheet3相交,只需要将sheet3生成的边e13和e14加入到相应的匹配边组中,然后创建新的e12和e15匹配边,并存入匹配边列表中。
二次切割生成的匹配边见表2,每组板架的切割使用一张表表示,并与被切割板架关联,以便在生成多面体模型时供缝合操作查询。
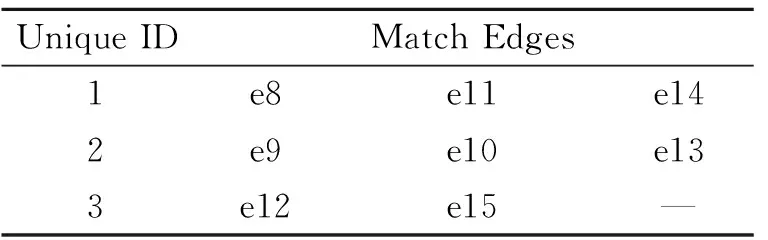
表2 二次切割匹配边列表
NX中CAD几何和多面体几何之间的对应关系见表3。由于CAD模型和多面体模型属于不同的模型,在进行多面体转换时,使用NX的查询API进行对应关系查询,将表2中的切割信息转换成表4形式,这样就可以在多面体几何中进行缝合。

表3 多面体几何和CAD几何对应关系
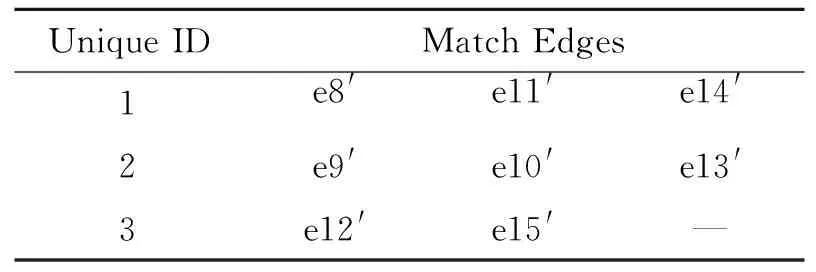
表4 多面体中匹配边列表
注:表2中e8为CAD几何中的边,表4中的e8′是多面体几何中的边,2种模型中的几何信息一一对应
2.3 相交板架在多面体模型中的缝合过程
为了能够在划分网格时实现网格的匹配,需要利用表4中匹配边信息实现多面体网格间的缝合。基本思想是从其中任意一条边的起点开始,向对方进行投影操作,然后进行多边形点的合并。
如图9所示,以船体外壳及相交的强肋骨为例进行介绍缝合的过程,主要存在2种情况。
1)以外壳上的p2点为起点,向强肋骨的投影,在设定的误差范围内,发现p1点和p2点重合,于是将p2点合并到p1点。
2)沿着边的方向,下一个需要合并的点是p3,将p3点向强肋骨投影,在误差范围内不存在可以合并的点,如图9b)所示;为了实现合并功能,需要在facet1的边上布置一个硬点p3′,将facet1拆分成2个片体,如图9c)所示,生成的facet1-1和facet1-2,直至完成2个多面体的合并,强肋骨和外壳就变成一个几何体。这样在划分网格时,基于一个多面体划分出的网格就会相互匹配,可减少对网格的缝合,快速建模网格模型。
3 划分网格
经过缝合处理后,多个相互独立的多面体结构被“焊接”成一个完整的多面体模型,通过使用NX中网格生成器将多面体模型网格化,再在网格上附上单元属性,设置好边界条件[15],采用Nastran等分析模块中进行有限元分析操作。
4 系统实现与应用实例
参考通用船舶有限元建模流程[16]。首先利用CAD设计模型生成关联的简化模型,根据船舶有限元建模需求进行模型简化,在简化模型中进行板筋和板板切割,存储切割的匹配边信息,将简化模型转换成多面体模型,完成边的缝合。对于在B-Rep模型中不能完成的简化操作,可以在多面体模型中进一步完成几何清理,最后直接对多面体模型进行网格划分,得到理想的有限元网格。
对180 000 t散货船中的舱段前处理示意于图10,板架切割公差5.0 mm。测试主机主要参数配置:Intel Xeon E3-1231 v3 CPU,8G RAM。舱段的板架切割耗时36min,多面体模型生成及匹配边“焊接”耗时50 min,网格生成耗时29 min,整个建模过程采用通用的建模方式大约需要几周时间。
由图10a)和b)可以看出,相交结构的单元相互匹配。
5 结论
基于NX11的CAD/CAE集成开发平台实现了从CAD模型到网格模型的自动生成,与通用的手工建模方式相比能够提高船舶有限元的建模效率。所提出的网格自动生成技术可以推广到更一般的有限元建模过程当中,提高整个有限元建模的效率。
