改进灰色模型在柴油机热工参数预测中的应用
2018-11-01唐盖盖傅祥棣邵广申
唐盖盖 傅祥棣 邵广申 陈 宁
(江苏科技大学 能源与动力工程学院 镇江212003)
引 言
灰色理论所要处理的问题是:利用某系统的已知信息去认知这个系统的特性、状态和发展趋势,并对其未来作出预测。灰色模型即灰色理论的微分方程模型。传统灰色模型为GM(1,1)模型,是一个一阶且一个变量的微分方程模型,因其模型结构简单且预测结果可信度较高而被广泛应用于工业、农业、交通领域的预测。由于船舶上对主要动力源柴油机安全性的关注度提高,GM(1,1)模型也逐渐被应用于船用柴油机的故障诊断,如对船用柴油机热工参数的预测[1-3]。但是,一般GM(1,1)模型是依据固定已知信息作为初始值建立预测模型的,对于船用柴油机长期运行机件磨损造成性能指标降低后产生的问题,其预测能力较差。为进一步提高GM(1,1)模型预测精度,很多学者提出了多种改进方法:在灰色GM(1,1)模型和线性回归模型的基础上结合有效度原理建立新的组合模型[4],对建模序列进行对数平滑处理,而后利用遗传算法对背景值进行寻优,形成改进的新陈代谢GM(1,1)模型[5];在灰色预测的基础上进行马尔科夫预测,利用马尔科夫状态转移矩阵来改进灰色系统模型[6]等,但其均未对GM(1,1)模型的基本构建参数进行修正。从根源上分析建模误差来源;文献[7-10]中对GM(1,1)模型构造参数中的初始值以及权数进行了修正,但没有建立动态模型,对于长期的预测性能较弱。笔者通过新陈代谢法建立动态GM(1,1)模型,进而修正了动态模型构建参数中的初始值、背景值权数以及模型维数,并通过仿真模型数据对其进行了预测精度分析,证实了最终改进后的动态GM(1,1)预测模型相对于文献[1]和文献[7]的GM(1,1)模型有更高的预测精度。
1 G M(1,1)模型建立与改进
1.1 一般G M(1,1)模型
一般的GM(1,1)模型的建立如下:已知一组已知量序列:
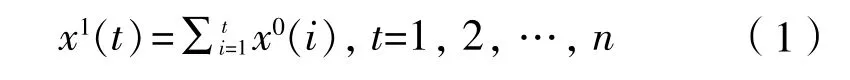
(2)对 作准光滑性检验:
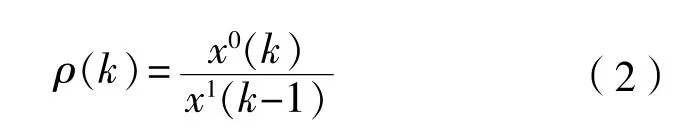
当k> 2时,若存在 < 0.5,则满足准光滑条件。
(3)对 做一般准指数规律检验:
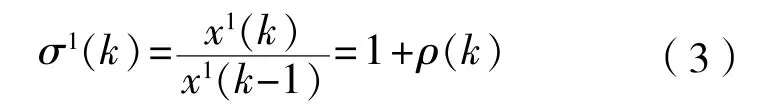
当k>2时,若存在 ,则满足准指数规律。
(4)若满足以上检验条件,则说明序列满足一阶线性微分方程:
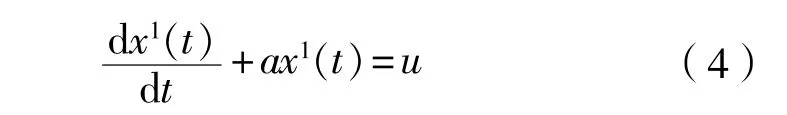
(5)对 做紧邻均值等权生成,得到式(4)的背景值:
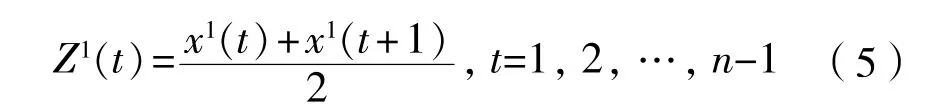
(6)对参数列 做最小二乘估计[11]得:

(7)将a和u带入GM(1,1)白化方程得时间响应函数:
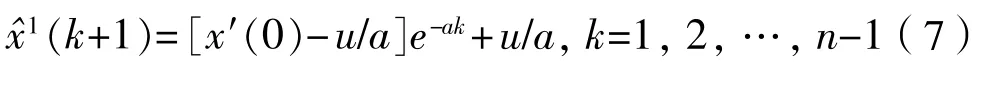
式中:k≥1,得到X1的模拟值:
(8)以 做累减还原,即可得到原始序列的预测序列[12]:
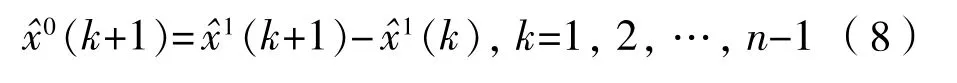
(9)检验模型精度:
采用相对误差(RPE)来衡量预测模型精度,RPE定义如下:
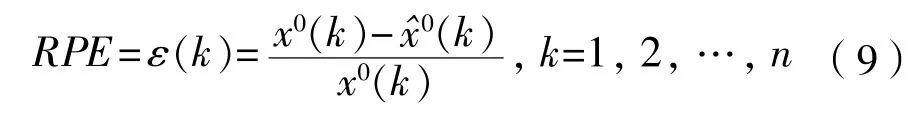
式中: 为第k个实际值, 为第k个预测值,模型最终的预测精度可由平均相对误差(ARPE)来衡量,ARPE定义如下:
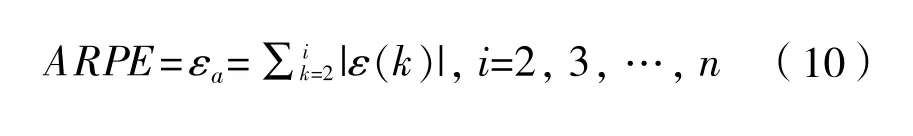
1.2 G M(1,1)模型改进
1.2.1 新陈代谢GM(1,1)模型
在实际情况中,针对船舶柴油机这个连续系统,随着时间推移,会不断产生新的数据以及新的未知波动,使系统的发展情况受到影响。从发展的角度看,随着系统长期发展,偏离时间点越远的数据对系统的描述是越弱的,所以在实际建模中,将不断地以新的数据替换之前的已知数据作为GM(1,1)预测模型初始值,也就实现了数据的新陈代谢,即新陈代谢GM(1,1)模型,对传统模型的长期性预测能力进行了有效的改进。建模方式如下:
像这样随着原始数据序列变化而更新的预测模型即为新陈代谢 GM(1,1)模型[13-14]。
1.2.2 模型构建参数修正
最小二乘估计法是一种数学优化技术,它通过最小化误差的平方和寻找数据的最佳匹配函数,可简便地求得未知的数据,并使这些求得的数据与实际数据之间误差的平方和为最小。为此,笔者将使用最小二乘法统一修正模型结构参数。
1.2.2.1 背景值权值修正
一般的GM(1,1) 预测模型在生成背景值时,为方便计算,采用等权生成,即 的相邻两项权值μ1和μ2均为 0.5(μ1+μ2=1),实际应用中并没有文献证明在μ1=μ2= 0.5时的预测模型精度最高。因此,笔者认为应在建模时用式(15)替换式(5),以μ1在[0, 1]内自增0.01的步长进行迭代寻优确定最优权值。
1.2.2.2 初始值修正
一般GM(1,1) 预测模型默认预测初始值为原始序列第一项 ,但实际上,该做法并不能保证针对各种应用条件下都能使模型预测误差最小,因此,根据最小二乘法原理进行修正初始值,修正方法如下:
(1)根据式(6),设最佳初始值为m,则GM(1,1)模型得出的原始序列估计方程为:

(2)模型预测值为:

(4)计算预测值与实际值的方差和S:

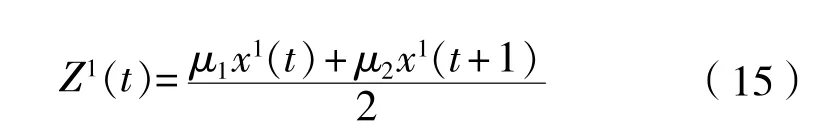
模型背景值和初始值并行修正算法见图1。

图1 模型初始值和背景值权值修正算法
1.2.2.3 维数修正
新陈代谢GM(1,1)模型虽然实现了随原始序列变化而更新,但其维数往往是一个人为设定的定值,易受到系统阶跃性数据的影响,民致模型预测精度降低。对于该问题笔者认为,应适当地保留几位历史数据,可以使预测模型更为平滑,受系统的阶跃性数据影响减小。在保证模型预测值与实际值方差最小的情况下,通过对历史数据的迭代建模进行寻优,从而确定预测模型最佳维数,寻优方法如下:
(2)第k次建模所取参数序列为:A1X0t={x01,x02,…,x0k+n},A2X0t={x02,x03,…,x0k+n},…,AkX0t={x0(k),x0k+1,…,x0k+n},然后修正初始值和背景值权值并建立GM(1,1)模型。
(3)分别计算所有模型的预测值与实际值的方差,取预测值和实际值误差的平方和最小的模型作为最优模型。
2 船用柴油机热工参数提取
2.1 船用柴油机仿真模型搭建
利用AVL Boost[15]仿真计算软件建立6100型船用柴油机仿真模型,其初始状态依据柴油机厂家提供的结构参数和实验台架数据设定。仿真模型图见图2,柴油机部分结构参数和初始参数值见下页表1。
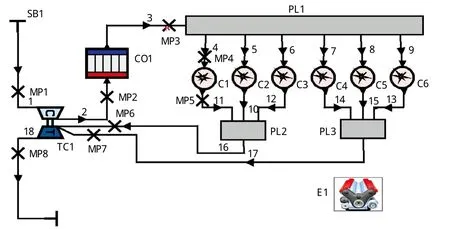
图2 柴油机仿真模型
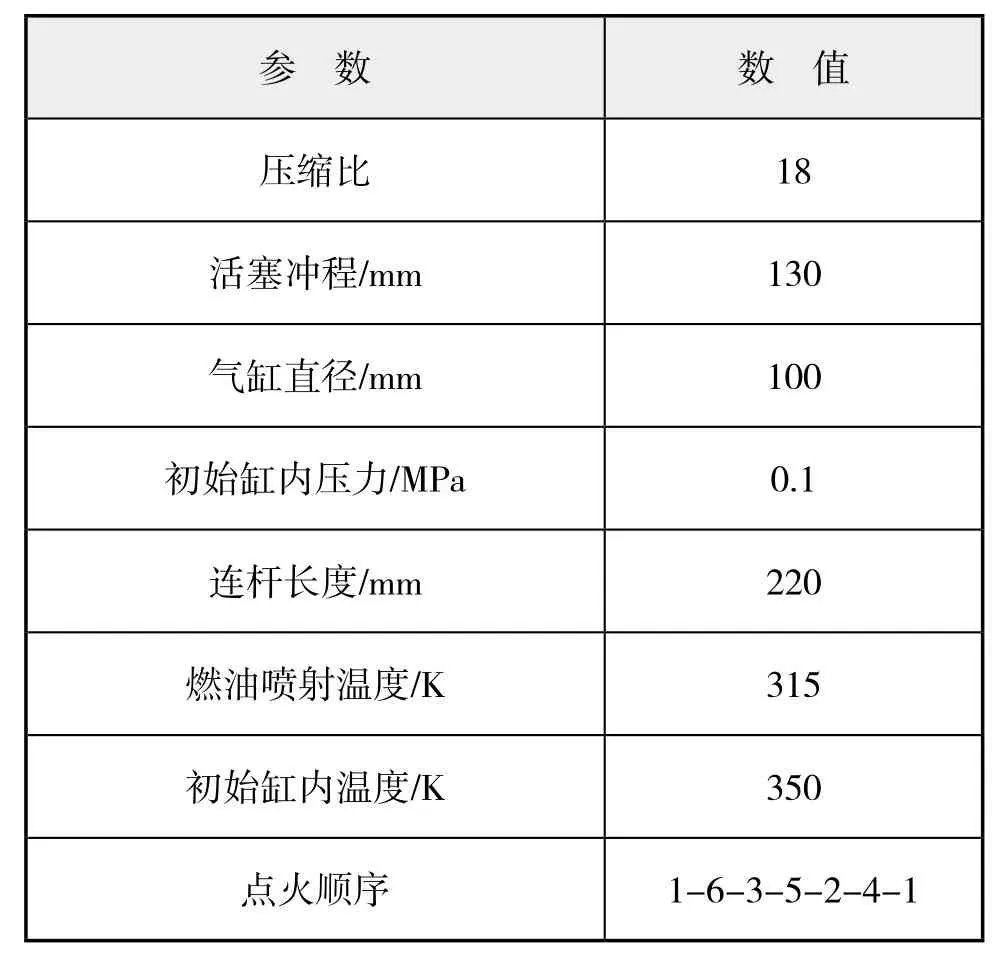
表1 柴油机主要结构参数和部分初始参数值
仿真模型主要包括:2个系统边界(SB1,SB2),空气冷却器,3个稳压腔(其中PL1为进气腔,PL2和PL3为排气腔),6个气缸模型C1~C6,一个涡轮增压器TC1,发动机主机E1,18个连接管,8个测点(MP1~MP8)。缸内热传民选用的Woschni1978,缸内燃烧模式为单VIBE函数,增压模型选择简易模型(Simplified Model)。
在外特性范围内,将仿真数据与试验台架数据做对比,结果见图3。其中(a)为缸内压力对比曲线,数值误差低于5%;图(b)为平均有效压力对比曲线,数值误差低于3%;图(c)为额定转速2500 r/min下的燃油消耗率对比曲线,吻合程度高。从以上结果可看出仿真数据与实验台架数据吻合较好,该模型满足仿真实验需求。
2.2 热工参数提取
对满负荷、额定转速工况下的柴油机仿真模型,通过调整其喷油量来模拟柴油机运行负荷的变化,负荷变化范围为100%~107%,增量为1%。计算完成后,提取部分柴油机热工参数,包括1缸内爆发压力P1,增压涡轮入口压力P2及进口温度T1,1缸排气温度T2及排气压力P3,共8组。其详细数据见下页表2。
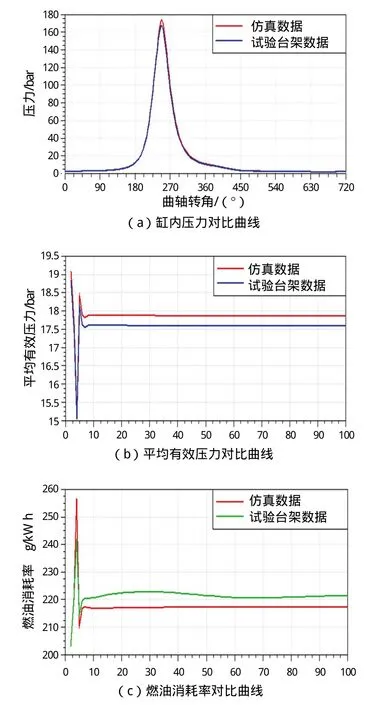
图3 仿真数据与试验台架数据对比
3 实例建模与精度分析
以表2的前4组数据作为建模数据分别建立一般G(1,1)模型、修正参数的G(1,1)模型以及修正参数的新陈代谢G(1,1)模型,然后取后4组数据来验证模型的预测精度。
(1)首先对建模数据做准光滑性检验和一般准指数规律检验,结果见下页表3。
由表3可看出,5种热工参数在取前4项作为建模初始数据时,当k>2时,存在 <0.5,满足准光滑条件;当k>2时,存在 ,满足准指数规律,因此均满足G(1,1)模型的建模要求。
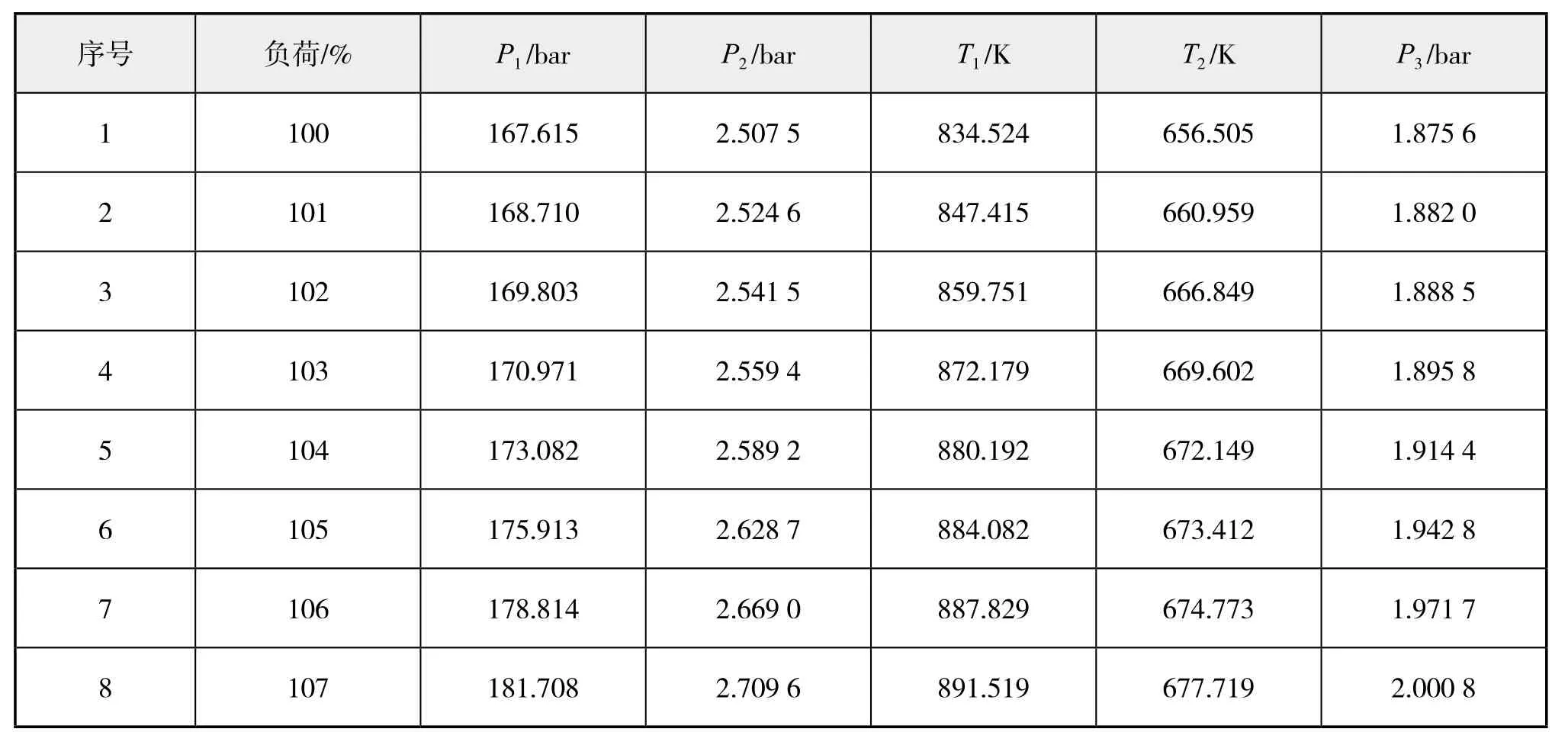
表2 柴油机部分热工参数值

表3 建模数据检验结果
(2)三种预测模型的预测结果见表4 -表6。
由表4 -表6可看出,一般G(1,1)模型、修正参数的G(1,1)模型以及修正参数的新陈代谢G(1,1)模型这三种模型的预测精度依次提高,修正参数的G(1,1)模型虽然较一般G(1,1)模型精度有所提升,但幅度较小,而修正参数的新陈代谢G(1,1)模型的预测精度较之前两种有较大改进,因为其“动态”不但体现在有新数据的实时更新,而且还有建模维数的自动修正,使预测结果更加精确。
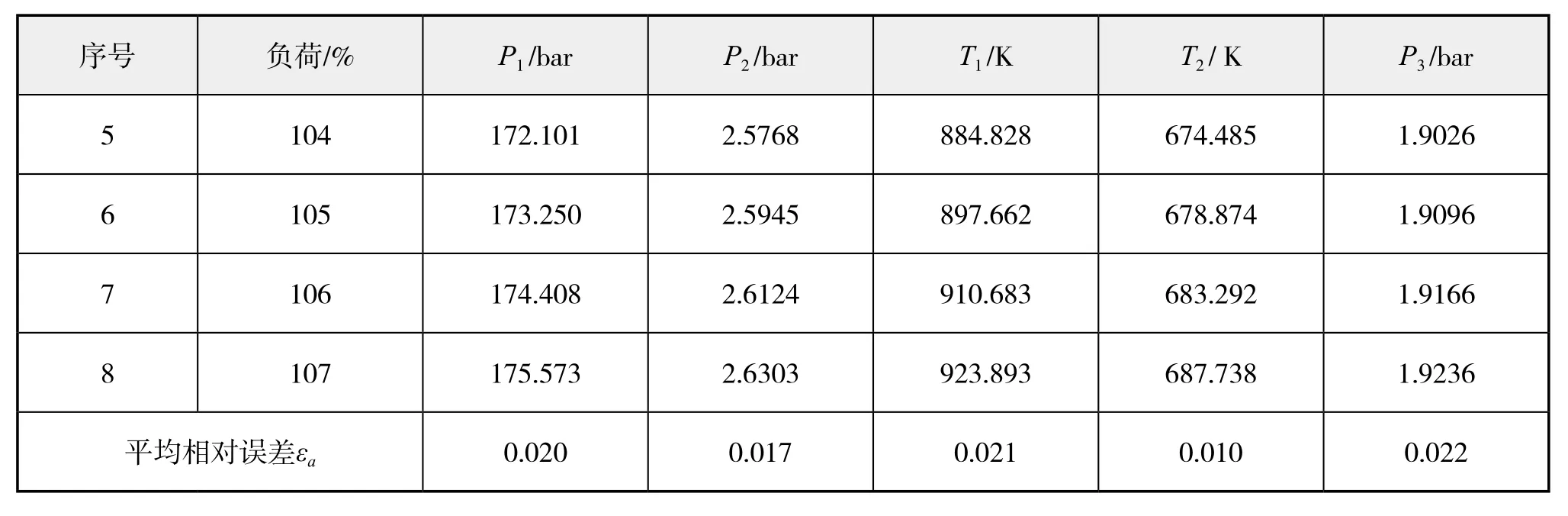
表4 一般G(1,1)模型预测结果
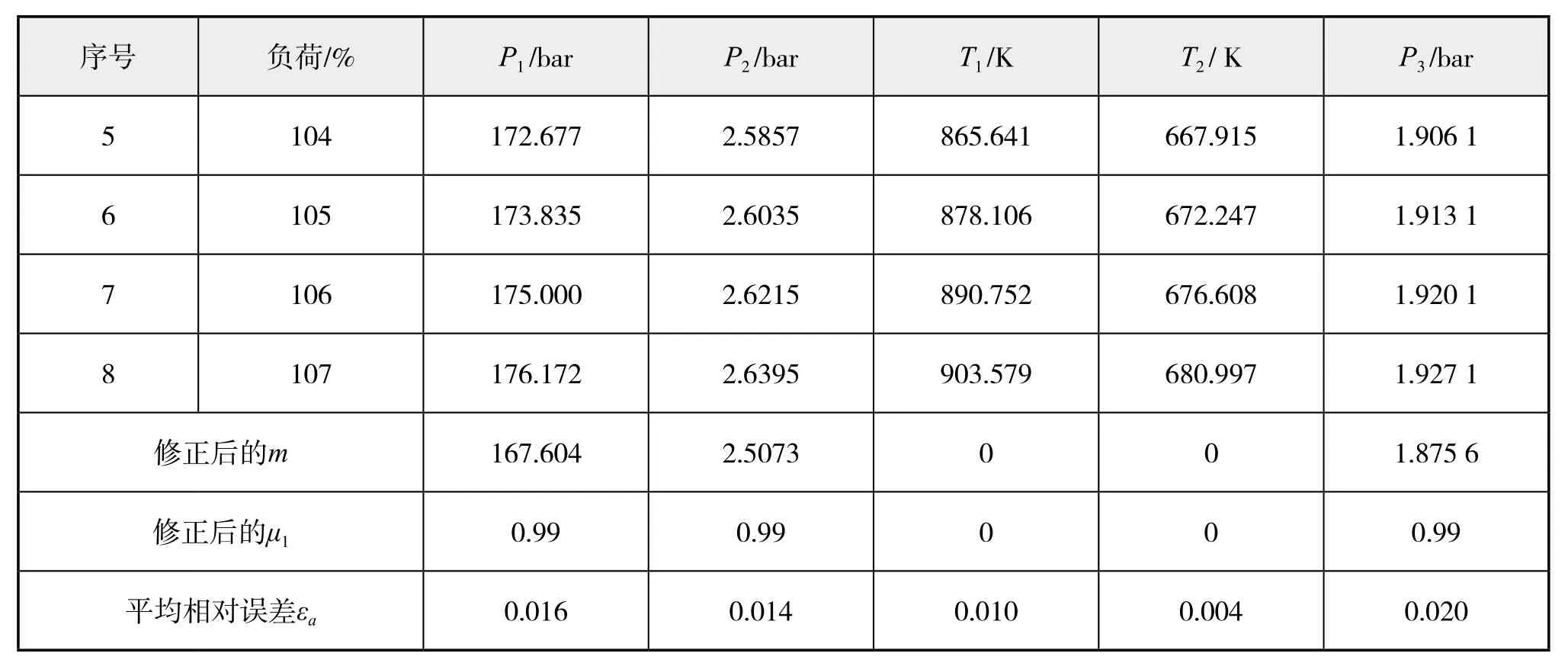
表5 修正参数的G(1,1)模型预测结果
4 结 语
通过对一般G(1,1)模型的初始值、背景值的权值修正,再基于新陈代谢原理建立了动态的G(1,1)模型,而后对动态模型的建模维数进行修正,形成最终改进的动态G(1,1)预测模型。而后,利用AVL Boost仿真计算软件建立柴油机仿真模型,在验证了仿真模型精度满足要求后,通过调整其喷油量来模拟柴油机运行负荷的变化,并提取部分热工参数作为验证预测模型的数据源,通过对三种预测模型计算结果的分析,结果表明最终改进的动态G(1,1)预测模型精度有很大提高,可以应用于实际柴油机维护中。
