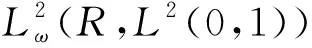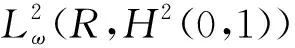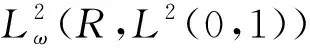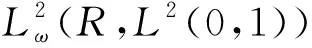一类非线性四阶抛物方程周期解的存在性
2018-10-31梁波吴晓琴张振宇
梁波,吴晓琴,张振宇
(大连交通大学 理学院,辽宁 大连 116028)*
0 引言
晶体是由物质的质点在空间中作有规律的排列而形成的物质. 晶体按照不同性质可分为离子、原子、分子、金属等四大典型类别.由于晶体内部结构中的质点的运动, 从而形成了一定形式的晶格, 外表上为具有一定形状的几何多面体.
由于各种不同的原因, 晶体原子在不同程度上会发生扩散, 导致晶体结构发生变化. 晶体中原子发生扩散是由原子所作的无规则的布朗运动所引起的. 并且, 原子在扩散过程中遵循一定的宏观扩散规律, 从而产生了扩散方程 :
ut=-jx+f(x,t)
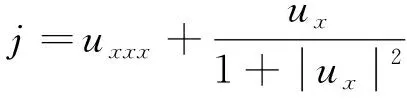
于(0,1)×R.
文中,将其进行改进得到所要讨论的四阶抛物方程
于(0,1)×R, (1)
u(x,t+ω)=u(x,t),x∈(0,1),t∈R
(2)
ux|x=0,1=uxxx|x=0,1=0,t∈R,
(3)
定理假定f∈Cω(R;H2(0,1)),ft∈Cω(R;L2(0,1)),问题(1)~(3)存在广义时间周期解
(4)
(5)
此定理为本文主要结论,下面将利用近似解估计给出证明.
1 近似解估计
令{yj(x)}(j=1,2,…)是L2(0,1)中的标准正交基,并且满足特征值问题
y″+λy=0,y′(0)=y′(1)=0
其中λj(j=1,2,…)为特征值.
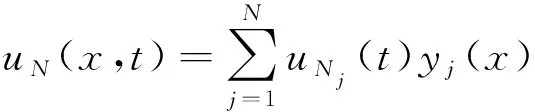
uNj(t)∈C1(ω,R)(j=1,2,…,N),
N是一个正常数. 由Galerkin方法,可知uN(x,t)在(0,1)×R满足方程
在应用Leray-Schauder不动点定理证明uN(x,t)是问题(6)~(8)的解时,考虑以下含参数θ(0≤θ≤1)的偏微分方程的时间周期解:
(9)
其中,θ∈[0,1],uN∈(0,1)×R. 依据线性方程理论,方程(9)存在唯一的解vN∈C1(ω,R).
从而定义映射:
T:[0,1]×C(ω,R)→C(ω,R),
(θ,vN)→vN.
显然,对任意的vN∈C1(ω,R),都可以满足T(0,vN)=0.而对vN∈C1(ω,R),满足T(θ,vN)=vN.
引理1映射
T:[0,1]×C(ω,R)→C(ω,R)
是紧映射.
证明:令
且存在常数M>0使得
‖vk‖C(ω,R)≤M,∀k>0
若uk=T(θk,vk) ,那么,根据Schauder理论(见文献[4])可知uk∈C1(ω,R)且满足
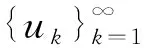
从而由Arzela-Ascoli定理知,uk在C(ω,R)中是收敛的.故映射T是紧的.
引理2假定f∈Cω(R;L2(0,1)),令
则问题(6)~(8)存在近似解uN,且有估计
(10)
其中,C0是不受N、M1的正常数.
证明:通过Poincare'和Hölder不等式,可得
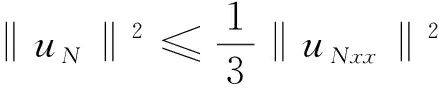
(11)
对于式(9)以uN为检验函数,在(0,1)上积分,由Hölder不等式可得
‖uNx‖2+C‖uN‖2+2‖f‖2
其中,0<δ<1. 从而有
(12)
由式(12)得
(13)
根据积分中值定理,存在t1∈(0,ω),使得
联合式(11)可得
(14)
将式(12)在[t1,t+ω](∀t∈[0,ω])上积分,由式(13)有
其中,C0是不受N,M1约束的正常数.
由引理1和引理2的证明,依据Leray-Schauder不动点定理可知,当θ=1时,式(9)的解uN是式(6) ~(8)的解.
引理3假定
f∈Cω(R;H2(0,1)),ft∈Cω(R;L2(0,1))
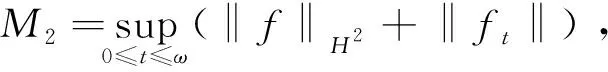
(15)
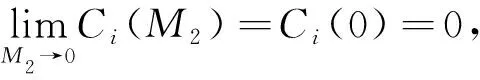
证明:对于式(6),以-uNxx为检验函数在(0,1)上积分可得
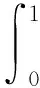
其中,0<δ<1.
由Hölder不等式可得
(16)
通过Gagliardo-Nirenberg不等式, 式(10)以及M1 将其代入式(16),应用Young不等式, 得 (17) 由式(17),应用积分中值定理,存在t2∈(0,ω),使 ‖uNxxx(·,t2)‖2≤C4(M2). 从而得到 再由式(17)可有 通过Sobolev嵌入定理,有 (18) 对于式(6),以uNxxxxxxxx为检验函数,并且在(0,1)上将其积分可获得估计 ‖uNxxx(·,t)‖C[0,1]≤C‖uN‖H4≤C9(M2) (19) 由式(6), 对任意的uN∈(0,1)×R有 (20) 对于式(20), 以uNxxxxt为检验函数, 并在(0,1)上积分,可得估计 ‖uNxt(·,t)‖C[0,1]≤C‖uNt‖H2≤C10(M2) (21) 联合式(19)和式(21)得到 通过上一小节引理给出的近似解的估计及证明,该部分借助以上估计对第一部分中的定理作出证明. 证明:通过式(15)和嵌入定理,有以下估计式 (22) 依据Arzela-Ascoli定理和式(22)可得,存在一个函数u(x,t)和{uN(x,t)}的子序列(仍记为{uN(x,t)}),当N→+∞时,{uN(x,t)}、{uNx(x,t)}在[0,ω]×(0,1)中分别一致收敛于u(x,t)、ux(x,t). 定义 综上可知,问题(1)~(3)存在广义时间周期解,并且满足式(4)和(5).2 结论证明