一种风电机组轴承简化建模方法的研究

0 引言

滚动轴承的应用非常广泛，不仅涉及到航天、船舶等领域，也涉及到风力发电设备[1]。对滚动轴承的分析起初采用的是动力学方法，对轴承的整个运动过程建立动力学方程，求得任意瞬间轴承各部件的运动参数和接触应力。目前，轴承的分析主要采用计算机建模，通过仿真的形式分析轴承的各相关性能指标[2]，但滚动轴承的仿真建模主要还是以实体建模为主，所需计算量非常大。因此，本文针对风电机组上的变桨轴承与偏航轴承，采用GAP单元简化轴承建模的方法，并用理论方法验证其正确性。结果表明，这种简化方法可有效模拟滚动轴承受力特性，对结构尺寸较大的轴承建模可起到一定的借鉴作用。

1 采用MSC.Marc/Mentat软件中的GAP单元对轴承滚动体进行分析

四点接触轴承有3个关键点，分别是滚动体中心点、滚动体与外圈接触点、滚动体与内圈接触点。四点接触轴承在受力的过程中，其荷载传递形式是直线形式，如图1所示。

图1 荷载传递路线

根据荷载的传递路径特征，在对轴承进行简化建模时，需充分考虑MSC.Marc/Mentat中的GAP单元特性，通过对单元特性的设置，完成最终模型的建立。

GAP单元支持MSC.Marc/Mentat软件中的任意其他单元连接，分为左右2个连接点，分别连接在模型的不同节点上，用以描述模型中任意两节点的相对关系(包含摩擦、滑动或热影响等)[3]。

1.1 实体滚动轴承参数及三维模型

采用三维软件对滚动轴承(以某一单排四点接触球轴承为例)进行建模，包含轴承内圈、轴承外圈、滚动体(模型中省略保持架，在后期的有限元分析软件中采用一个微小弹簧代替保持架)来实现滚动体的固定。此模型建立比较简单，具体如图2所示。轴承各参数如表1所示。

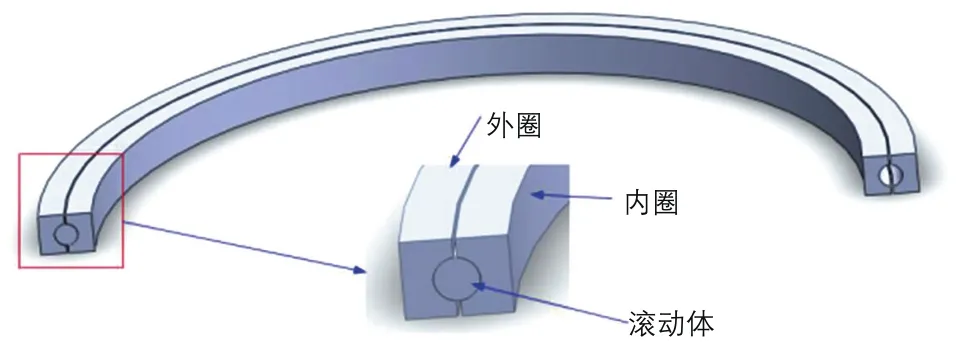
图2 四点接触球轴承三维模型

表1 四点接触球轴承参数表

1.2 滚动轴承的简化建模分析

1.2.1 GAP单元的特性

假设B点代表外圈接触点，C点代表内圈接触点，那么B、C两点可组成GAP单元，B、C两点之间的距离可设定为滚动体的直径Dw。当轴承受外界作用力时，GAP单元可出现荷载－位移关系，其关系可通过接触面的切向分量和法向分量来表述[4]。在接触区域，为了防止接触体相互侵入，GAP单元的法向刚度将变得足够大；而在未接触区，它对分析对象的运动状态不产生影响[5]。

当接触点对的相对位移大于初始间隙时，法向力Fn的值就会是零，而接触点对就会处于分离状态，这时GAP单元不会发生力的传递，从而不会影响分析对象的运动状态；而当相对位移小于初始间隙时，表明接触点对处于接触状态，此时GAP单元就像一个线性弹簧，其法向接触刚度为KA，在GAP单元的法线方向就会存在一个法向力Fn(负值)，内外圈就会通过GAP单元在B、C两点之间传递荷载。

1.2.2 GAP单元对轴承的简化建模

轴承三维模型建好之后，要对模型进行网格划分。网格划分是否合理将关系到后期模型计算的准确性和效率，所以网格要过渡合理、均匀；同时网格类型的选择也至关重要，因网格类型有四面体、六面体、八面体等，每种类型适用于不同的模型，此处是对单个轴承进行分析，为了达到使用较少的网格重划分次数而得到较高计算精度的目的，最终选择六面体网格。

因轴承整圈具有左右对称性，只取半个轴承模型进行分析，滚动体也只取半个进行实体建模(只考虑此滚动体的应力应变情况，与理论计算进行对比)，其他的滚动体只考虑力的传递，不再具体分析每个滚动体的应力应变，在这里将其他滚动体用“GAP单元”来替代定义。刚度是滚动轴承的一项重要指标，而GAP单元就像一个线性弹簧，将其长度设置为滚动体直径后，在软件中再将其初始轴向刚度和径向刚度设置为零(初始状态不受力)，一旦轴承承受外界作用力，GAP单元可出现荷载－位移关系，轴向刚度和径向刚度就会出现一定的数值，接触刚度这时就可近似模拟滚动体刚度[6]。

接触角是滚动轴承的一个主要设计参数，在分析轴承受力、变形、运动关系和确定轴承承载能力时，都需要首先确定接触角的大小。GAP单元由2个节点连接组成，一定数量的GAP单元可以近似代替一个滚动体，也就是在建立之初就已经指定了力的传递点，所以GAP单元无法精确描述接触角的具体数值。这里针对接触角不做具体分析，但GAP单元越多，越能更准确地反映滚动体和滚道之间的接触情况。

GAP单元可以模拟任意直径滚动体建模，只需在软件中将GAP单元长度设置为滚动体直径即可。

所谓一定数量的GAP单元代替一个滚动体，并不是说GAP单元越少越好，也不是越多越好。GAP单元太少时，不足以模拟滚动体与滚道的接触状态；而GAP单元太多时，就会增加软件计算时间，降低效率。笔者前期已做过大量实验验证，为了使简化模型更好地与理论吻合，GAP单元需要均匀布置到接触角范围内，相邻GAP单元之间的角度差应控制在1°～3°之间。本模型采用14对GAP单元代替1个滚动体，相邻GAP单元之间的角度差约为2.14°(本模型轴承接触角为 30°)。

网格划分单元的大小根据位置有不同的取值，其在内外圈接触的地方大小约为2 mm，其他地方单元格可适当放大，如图3所示。

图3 基于GAP单元的滚动轴承简化建模

1.2.3 保持架的模拟

在MSC.Marc/Mentat软件中，选用刚度很小的弹簧单元对滚动体进行固定，小弹簧的作用类似于保持架，将各滚动体固定，并且均匀隔开。为了准确模拟保持架的作用，弹簧的一端与滚动体上节点相连，另一端设置为接地不动，如图4所示。

图4 弹簧单元固定滚动体

1.2.4 接触设置

接触设置主要是滚动体与内、外圈之间的状态设定。首先，针对GAP单元，根据软件中的要求，不需要对其进行接触设置，只需将其与内、外圈节点连接即可；其次，对半个滚动体与内、外圈的接触设置，这里设置为接触，即“touching”状态；最后，对其他参数进行设置，因为内圈、外圈和滚动体都假定采用轴承钢，材料为GCr15，所以将它们设置为可变形体，相应的摩擦系数设置为0.15。

1.2.5 边界条件、荷载的设置

1)边界条件的设置：滚动轴承受力时，其运动状态是不固定的，可以在轴承外圈上设置约束条件，同时对轴承内圈施加荷载；也可以在轴承内圈上设置约束条件，同时对轴承外圈施加荷载。在这里采取对外圈进行固定的方式，即对外圈采用全约束方式，同时约束轴承剖面沿法向的平动自由度，以及约束内圈沿轴向的转动自由度。

2)荷载的设置：以上边界条件设置好之后，开始在轴承内圈上加载来计算轴承接触部位各应力变化。根据MSC.Marc/Mentat软件对MPC点的介绍，这种点可以作为一个荷载施加中心，通过与模型相连，将荷载传递到模型上。此例中，将MPC点设置在轴承中心点处，并且将此点与内圈上表面所有点相连，荷载的传递路径就是通过这些连线进行传递。MPC点设置好之后，在其上面施加混合荷载(包含翻转力矩、径向力和轴向力)。

边界条件的设置及荷载的施加如图5及表2所示。

图5 边界条件、荷载设置示意图

表2 荷载值大小

1.2.6 滚动轴承简化建模有限元计算结果

根据表2中的相关参数，可以得到滚动轴承的应力和应变结果，其中，内圈与滚动体之间的最大接触应力值约为4603.2 MPa，最大位移值约为0.1511 mm；外圈与滚动体之间的最大接触应力值约为4521.6 MPa，最大位移值约为0.1465 mm。

内、外圈与滚动体接触的应力云图如图6、图7所示。

图6 内圈与滚动体接触的应力云图

图7 外圈与滚动体接触的应力云图

2 滚动轴承理论计算

理论计算采用的轴承模型与有限元计算模型一致，参数表和荷载表也采取表1、表2中的数据。

2.1 径向位移δr、轴向位移δa和倾斜角θ数值的确定

四点接触轴承在受力时，会发生一定的位移。要通过理论方法计算轴承在荷载作用下的相关量，首先需要确定3个未知量：径向位移δr、轴向位移δa和倾斜角θ，具体如图8所示。

图8 3个未知量示意图

针对以上3个未知量，需要根据文献[7-9]对其进行如下推导求解。图9是在混合荷载作用下，对轴承外圈固定，轴承内圈曲率中心轨迹的变化曲线。其中，S为受载时内、外圈滚道曲率中心之间的最短距离。图10为滚动体与滚道未加载与受载后的接触示意图，初始接触角α0的取值为π/4。

图9 内、外圈滚道曲率中心改变后轨迹示意图

图9、图10中的其他主要参数可通过下文中的公式进行确定：

式中，δi为受载后内圈曲率中心位移量；δo为受载后外圈曲率中心位移量。

所以，受载后内、外圈曲率中心变化总量δn为：

图10 滚动体与滚道未加载与受载后的接触示意图

内圈与滚动体之间的主曲率之和∑ρi可表示为：

轴承内圈辅助变量F()ρi可表示为：

图11 内圈与滚动体接触示意图

式中，ρ1为滚动体与内圈接触时的主曲率，ρ2为滚动体与外圈接触时的主曲率，且为内圈滚道圆弧曲率，为轴承内圈沟底曲率，

根据式(3)、式(4)的推导，同理可得出轴承外圈辅助变量F()ρo及外圈与滚动体之间的主曲率之和

内圈滚道曲率中心点半径Ri为：

外圈滚道曲率中心点半径Ro：

滚动体总共有84个，假设其中某个滚动体的中心在X轴上，设其与X轴夹角为ψ，则初始值ψ0=0，其他滚动体在滚道圆周上均匀分布，那么绕其逆时针方向分布的第i个滚动体，其的范围在[0,2π]之间，如图 12 所示。

图12 滚动体在滚道上的分布

根据参考文献[9]，图9中S值可表示为：

将式(7)带入式(2)可得：

某个滚动体上所受荷载Qψi为：

式中，K为滚动体与滚道接触的总刚度值；对于球轴承而言，n取1.5。

K可由式(10)求得：

式中，Ki为轴承内圈与滚动体之间的相对刚度；Ko为轴承外圈与滚动体之间的相对刚度。

其中：

对每个滚动体上的力进行分解，使每个滚动体上的受力均分解为与初始径向力Fr0、轴向力Fa0以及力矩M0相同方向的分力，然后对各分力在各自方向上分别求和，具体如下：

式中，α为轴承受载后的接触角，则有：

由此可推导出式(18)～式(20)：

轴承所受荷载如表2所示，根据式(16)～式(18)，可分别计算轴承的初始径向位移δr′(仅受径向力时)、初始轴向位移δa′(仅受轴向力时)、初始倾斜角θ′(仅受弯矩时)。

计算出各初始参数后，可根据牛顿迭代法进行收敛计算，具体如下[10]：

其中：

根据以上计算所得的3个初始值，将式(16)～式(18)联立，采用牛顿迭代法进行求解。求解的过程是迭代收敛的过程，当最终收敛后，就会得到轴承在外荷载(见表2)作用下的径向位移δr、轴向位移δa和倾斜角θ。

根据表1、表2中的数值及以上相关公式，可求得轴承其他参数值，具体如表3所示。

表3 计算所得参数值大小

2.2 接触应力、位移求解

首先计算84个滚动体所受的荷载大小，可通过计算所得的轴承3个未知量(轴向位移δa、径向位移δr和倾斜角θ)，结合公式(9)得到。针对以上有限元的计算结果，理论计算为了能与有限元模型更好的匹配，选择同一位置处的滚动体进行荷载理论计算，即取ψ=π，则计算所得滚动体的荷载Q=58708.58383。

2.2.1 轴承内圈与滚动体接触的最大应力及位移值

根据式(3)、式(4)及表 3可知，∑ρi=0.061145401，F(ρi)=0.6309204。

内圈与滚动体接触的最大接触应力pimax为：

根据F(ρi)的值，查《球轴承的设计计算》[9]中的赫兹接触系数表，并利用插值法可得：πeaiebi= 1.96082836 ×10-3、eδi=2.48944154× 10-4，则pimax=4614.5 MPa。

滚动体与内圈的最大位移δi为：

将相关数值代入式(24)可得δi=0.1481 mm。

2.2.2 轴承外圈与滚动体接触的最大应力及位移值

参照轴承内圈与滚动体的接触计算，同理可计 算 出 ∑ρo=0.05948664、F(ρo)=0.6206288、则轴承外圈与滚动体接触的最大接触应力值最大位移δo=0.1475 mm。

3 对比分析

基于理论计算的结果与GAP单元对轴承的简化建模计算结果进行对比，具体如表4所示。

表4 结果对比

根据表4中的数值可知，GAP单元建模计算的结果与理论计算的结果误差较小，基本吻合。

4 结论

本文采用有限元分析方法，用GAP单元模拟轴承内、外圈的接触，然后在添加外荷载的情况下对模型进行静强度分析计算；同时，采用理论方法，在同种工况下对该轴承分析计算，针对两种不同方法的计算结果分析对比，可得到以下结论：

1)GAP单元建模计算结果与理论计算结果误差较小，吻合度高。

2)GAP单元模拟轴承滚动体进行建模，可实现轴承内、外圈力的传递。

3)当不针对滚动体进行分析时，可用GAP单元代替所有滚动体进行简化建模，不会影响其他连接部件的计算结果。

4)GAP单元无法精确模拟轴承接触角的具体数值，只能近似模拟滚动体与滚道间的接触情况。要研究接触角时，需采取实体建模进行分析。

5)GAP单元模拟滚动体对轴承的简化建模，克服了实体轴承建模难度大、复杂性高的缺点，同时也大幅提高了计算速度。

6)这种简化方法可以应用于风力发电机组中变桨轴承及偏航轴承的建模，从而为风电轴承建模提供一种新的思路。