基于改进广义S变换的复赛谱时频域反褶积方法
2018-10-31刘春成巫南克
刘春成, 周 慰, 牛 聪, 龙 丹, 巫南克
(1.中海油研究总院,北京 100027; 2.成都理工大学地球物理学院,四川成都 610059)
随着地震勘探中对复杂构造储层精确描述的难度逐渐增大,运用反褶积方法来实现高分辨处理已经成为一种最常用的手段。Robinson等[1]假设地层反射系数满足白谱特性,提出了预测反褶积模型,后来又补充引入Wiener滤波,得到了广义的最小平方反褶积。为了摆脱这种假设,Robert等[2]将地震记录振幅谱转换到复赛谱中,假定子波是低频的,反射系数是高频的,以一种非线性滤波的方式来提取子波。Wiggins[3]提出最小熵反褶积,通过求解线性算子,使道集中的尖脉冲特性得到加强来进行反褶积。Milton等[4]提出一种混合相位反褶积方法。以上反褶积方法都是基于地震波始终保持不变的理想条件下,但是实际传播过程中其会受到地下介质的影响,产生能量的耗散效应,主频会随着传播时间的增长而向低频偏移,因此传统的褶积模型不吻合于这个动态过程。为了更加符合实际地震波传播规律,同时也考虑到大地滤波效应,Clarke[5]最早提出了时域非平稳反褶积方法。对于时频域地震模型,Rosa[6]结合Ricker研究结论认为,假设地震子波振幅谱是光滑的,可以平滑地震道将子波提取出来。唐博文、赵波等[7]对地震记录求二次谱,提出了一种新的子波提取方法,实现了谱模拟反褶积。Margrave等[8-9]将地震记录转换到Gabor域,假设地下反射系数满足白谱特性,通过对每个时间点振幅谱平滑,直接估计出衰减子波振幅谱,实现了时频域反褶积。周怀来等[10]在S域中实现动态反褶积,弥补了Gabor变换时窗固定的缺陷,但是没有从根本上摆脱反射系数满足白谱特性的假设。笔者通过对比Gabor变换、S变换[11]、改进广义S变换这3种时频分析方法,证明改进广义S变换在时频分析过程中的优越性;通过调节改进广义S变换得到参数获得衰减地震道的时频谱,将其转换到复赛谱时频域,通过多项式平滑的方式提取出子波振幅谱,从而推导出一种基于改进广义S变换的复赛谱时频域反褶积方法。
1 方法原理
1.1 改进广义S变换
对给定平方可积的信号x(t)的S变换[11]为
S(τ,f)=
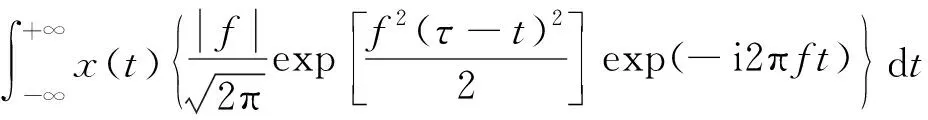
(1)
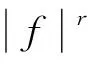
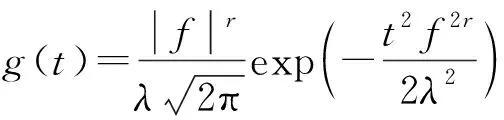
(2)
因此得到对给定信号x(t)的一种两参数改进广义S变换为
Sg(τ,f)=

(3)
式中,Sg(τ,f)为x(t)在S域中时频谱值;λ和r为高斯窗调节参数。
改进广义S变换与快速傅里叶变换直接联系,因此可以利用快速算法实现其逆过程:

(4)
1.2 复赛谱时频域反褶积模型
传统的时间域地震道卷积算法可以表示为
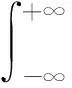
(5)
式中,地震道s(t)可以由时间域的反射系数r(t)和震源子波ω(t)的卷积表示;n(t)为干扰噪声。
在不考虑噪声的影响下,引入衰减函数a(τ,f)和衰减因子Q来描述地震子波在频率域中的衰减,衰减函数表示为
|a(τ,f)|=exp(-πfτ/Q).
(6)
综合推导出频率域的衰减褶积模型[11]:

(7)
将式(7)扩展到S域中,可以将衰减地震道的改进广义S变换时频谱Sg(τ,f)近似等同于子波频谱ω(f)、衰减函数a(τ,f)和反射系数时频谱值Rg(τ,f)之间的乘积[10,12],即
Sg(τ,f)≈ω(f)a(τ,f)Rg(τ,f).
(8)
只考虑地震道的振幅谱,式(8)可以表示[12]为
|Sg(τ,f)|≈|ωa(τ,f)||Rg(τ,f)|.
(9)
其中衰减子波的振幅谱值|ωa(τ,f)|可以表示为|ωa(τ,f)|=|ω(f)||a(τ,f)|。
时频域地震模型可以看作是一个时变系统,直接求出时变子波比较困难。Rosa[6]结合Ricker研究结论认为:假设反射系数具有白谱特性,其只影响地震道振幅谱的细节,而子波决定地震道振幅谱大体形状,因此子波可以通过平滑地震道的方式提取出来。传统的子波提取函数为
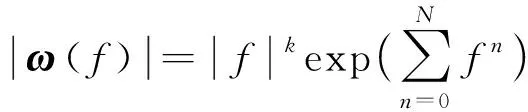
(10)
为了摆脱这种反射系数是白谱特性的假设,本文中将每个时间点的非平稳地震道时频谱变换到复赛谱时频域。记衰减地震道时频谱Sg(τ,f)变换到复赛时频域中为Slog(τ,f),即
Slog(τ,f)=log(|Sg(τ,f)|).
(11)
由于反射系数一般都是高频的,子波是低频的,在复赛时频域中能够很好地将两者分离,减小反射系数对子波形状的影响,因此对复赛时频谱使用多项式拟合(ployfit),平滑地震道消除反射系数的影响:
Sfit(τ,f)=ployfit(Slog(τ,f)).
(12)
换算平滑后的复赛时频谱,近似得到子波时频谱|ωfit(τ,f)|为
|ωfit(τ,f)|≈exp(Sfit(τ,f)).
(13)
在S域中利用Sg(τ,f)和|ωfit(τ,f)|就可以得到反射系数时频谱值R(τ,f),再对其进行S反变换得到时间域的r(t):
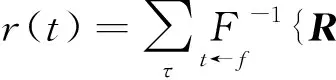

(14)
为了防止分母出现零值引入参数μ,Amax表示动态子波时频谱|ωfit(τ,f)|的最大值。
由于以上模型,受μ值影响很大,使得算法缺乏稳定性,本文中对以上模型进行优化,得
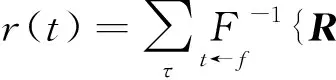
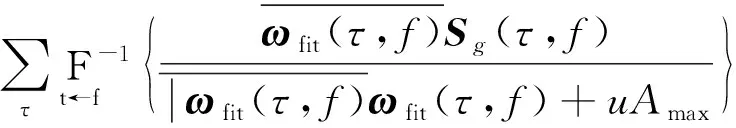
(15)

2 模型论证
以40 Hz雷克子波与随机反射系数褶积合成一个非平稳地震记录[12]。利用改进广义S变换对单道地震记录进行时频谱分析[13],取其中一个时间点振幅谱,如图1(c)黑色实线,展示出原始的非平稳地震道振幅谱明显受反射系数影响波动很大。利用式(11)对其取复赛谱,结果如图1(a)红色实线所示;在复赛谱中反射系数对低频的子波影响更小,用式(12)对其平滑得到结果如图1(a)黑色点线所示,将平滑后的复赛谱利用(13)式恢复到时间域得到子波振幅谱如图1(c)中黑色点线所示。对原始雷克子波求振幅谱,结果如图1(c)中红色实线,将复赛谱域提取的子波与其对比,可以明显地得到二者吻合,验证了复赛谱提取子波的可靠性;依次将非平稳地震道时频谱转换到复赛谱时频域,并对每个时间点平滑处理得到结果如图1(b)。对平滑结果利用式(13)换算得到时变子波时频谱,结果如图1(d)所示,得到时频域子波振幅谱。

图1 复赛谱时频域提取子波振幅谱Fig.1 Estimated wavelet amplitude spectrum in cepstral time-frequency domain
为了检验各个时频分析方法的效果,用20~120 Hz线性递增变化的调谐信号和120~20 Hz线性递减变化的调谐信号组合成一个复合信号如图2(a)[14],分别使用Gabor变换、S变换[15]、和改进广义S变换对其进行时频分析得到结果分别如图2(b)、图2(c)、图2(d)。可以看到Gabor变换对调谐信号的频率变化趋势有很好的描述,但是整体频率分辨率不够高,且在中间位置不能很好地将两个不同的调谐信号分开;当复合信号处于低频时,S变换具有很高的时频分辨率,但随着复合信号由低频到高频变化,其时频分辨能力越来越差;取改进广义S变换λ=0.8,r=1.4,增加窗函数对频率变化的敏感程度,提高时频聚焦性,对复合信号进行分析,结果如图2(d)所示,对比上述两种方法,该方法能更好地检测到复合信号的频率变化趋势,时频分辨率更优。
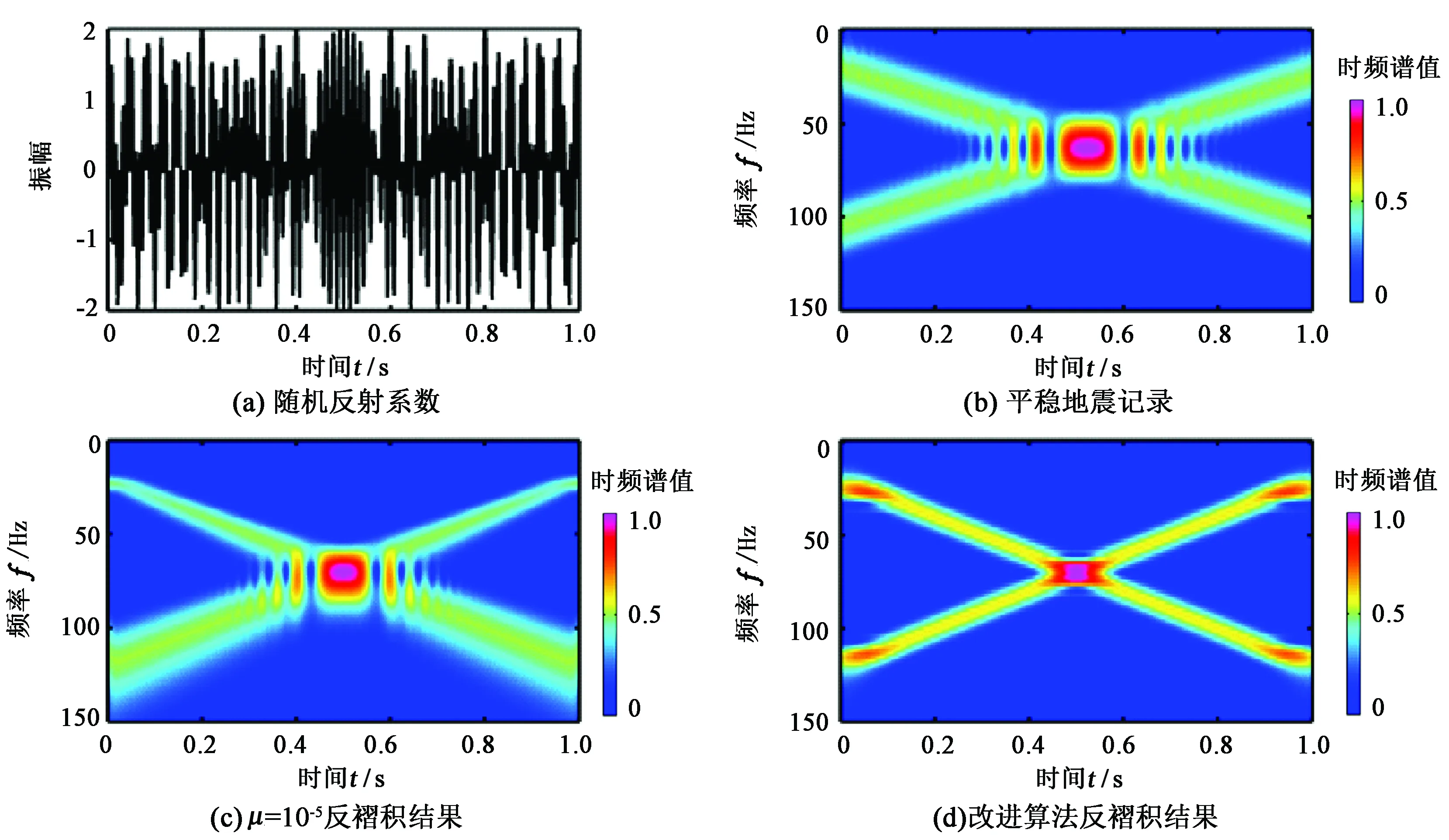
图2 复合信号时频分析Fig.2 Time-frequency analysis of composite signals
建立理论模型验证改进后的时频域反褶积算法的稳定性。模拟地下反射系数如图3(a)所示,使用主频为40 Hz的雷克子波利用式(5)得到合成单道地震记录结果如图3(b)所示,利用式(14)对图3(a)单道地震记录进行反褶积处理,其中μ取值为10-5,得到反褶积结果如图3(c)所示;取同一μ值利用本文改进之后的算法式(15),得到反褶积结果如图3(d)所示;由于提取子波时算法近似带来的误差和μ值不确定性的影响,导致反褶积结果出现图3(c)中额外假震荡,经过改进后的算法,提高了系统稳定性,抗μ值干扰能力增强。

图3 改进算法稳定性研究Fig.3 Stability research of improved algorithm
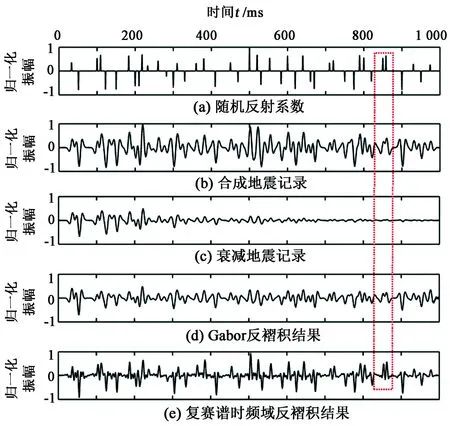
图4 反褶积结果对比Fig.4 Comparison of deconvolution results
将复赛谱时频域反褶积与Gabor反褶积结果进行对比。生成一个随机反射系数如图4(a)所示,利用式(5)使用主频为40 Hz的雷克子波与其褶积产生一个平稳地震记录如图4(b)所示,对其时频分析结果如图5(a)所示;引入Q值为50的衰减函数[16],结合式(7)得到一个非平稳地震道[17]如图4(c)所示,其时频分析结果如图5(b)所示,对非平稳地震道进行Gabor反褶积得到的结果如图4(d),其时频分析结果如图5(c)所示,图4(e)是使用本文复赛谱时频域反褶积处理得到的结果,其时频分析结果如图5(d)所示;观察发现复赛谱反褶积结果整体比Gabor反褶积结果更加收敛,且与图4(a)中的反射系数对照更加吻合;对比图4中红色虚线标记的位置,可以发现Gabor反褶积很大程度上只是对衰减地震道能量上的恢复,而基于改进广义S变换的复赛谱时频域反褶积,在恢复地震波衰减能量的基础上,压缩了地震子波,能清楚地区分出两个薄层,提高了地震分辨率[18];从图5时频分析结果也可以看出复赛谱反褶积结果在恢复能量的同时,拓宽了频带,这说明本文的方法更优。基于前面对单道地震信号处理效果详细分析描述基础上,建立一个二维速度模型[19](图6),对比分析两种反褶积算法分辨率。分别在200、300 m的位置假定两个薄层,在400 m位置设计一个楔形。将速度模型转换成反射系数,用30 Hz的雷克子波[20]与其卷积得到二维地震剖面,结果如图6(a)所示;结合式(7)得到衰减地震剖面如图6(b)所示,分别用Gabor反褶积和复赛谱反褶积对衰减地震剖面处理,得到结果分别如图6(c)、图6(d)所示。可以直观看出,两种反褶积方法对衰减剖面的能量都有恢复作用;在200 ms位置,复赛谱反褶积处理后两个负反射层能够很明显地分开,但是Gabor反褶积处并没有完全消除子波旁瓣的影响,对薄层识别能力不强;同样,在300 ms位置处,复赛谱反褶积对子波压缩的能力更强。注意图中黑色竖线位置,复赛谱反褶积在第10道就可以将楔形模型的两个反射层完全分离,而Gabor反褶积在第14道才能分离这两个子波,这说明复赛谱反褶积方法时间分辨率更高。
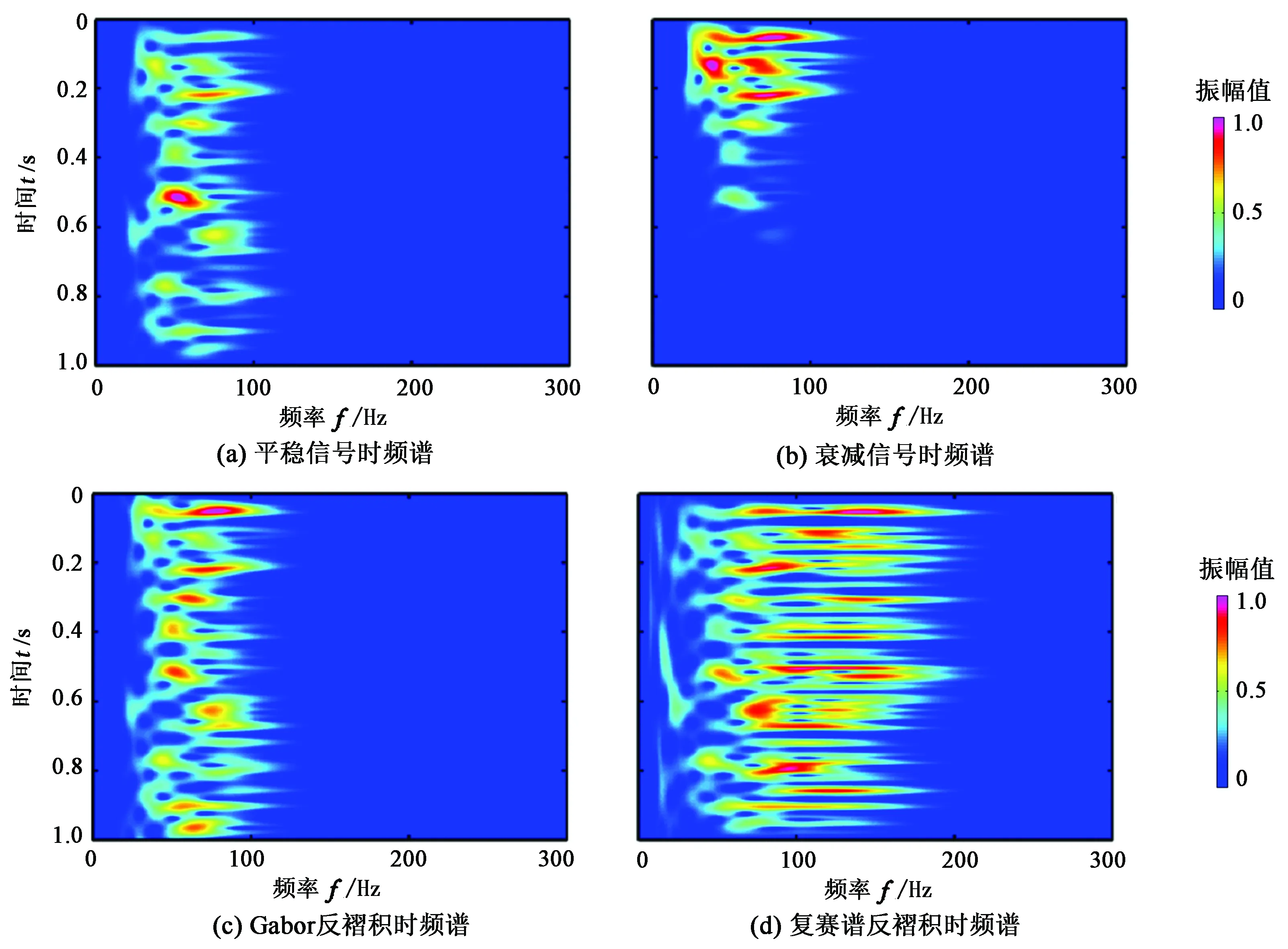
图5 不同信号时频谱Fig.5 Time spectrum of different signal
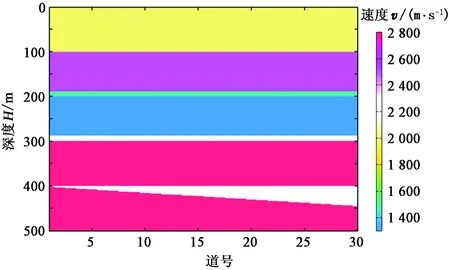
图6 速度地质模型Fig.6 Velocity geological model

图7 二维模型反褶积结果对比Fig.7 Comparison of two-dimensional seismic model deconvolution result
3 实际资料处理
为了验证本文方法对海上数据的实用性,选取中国南海某海域地震数据进行复赛谱时频域反褶积处理。研究区域构造背景上是深水沉积水道砂岩储层气藏,砂岩呈条带分布状,且分布局限,为了更好地识别储层,使用本文的方法进行高分辨处理。选取目的层区块如图8(a)所示,图8(b)和图8(c)是经过Gabor反褶积和复赛谱时频域反褶积方法处理之后的地震剖面。总体来看,两种方法反褶积处理后对整个剖面的同相轴都有一定的压缩作用。在图8中红色椭圆标记的位置,复赛谱时频域反褶积处理后成功识别出两个薄气层,而Gabor反褶积没有区分出这两个薄层;在图中两个红色箭头位置,复赛谱时频域反褶积也成功地恢复了弱反射层的能量,且与井曲线对照一致,准确地识别出下方的薄气层和油层;同时对比发现复赛谱时频域反褶积处理之后的剖面整体成层性更好,与井曲线对照更加准确;这说明了本文方法在南海数据高分辨处理的有效性。将这两个剖面进行综合振幅谱分析得到结果如图9所示,蓝色线是原始剖面的综合振幅谱,绿色线是Gabor反褶积处理后的剖面综合振幅谱,红色线是复赛谱时频域反褶积处理后的剖面综合振幅谱,可以看到复赛谱时频域反褶积处理后,在保留了原始剖面的低频信息的基础上,更好地拓宽了高频部分频带。
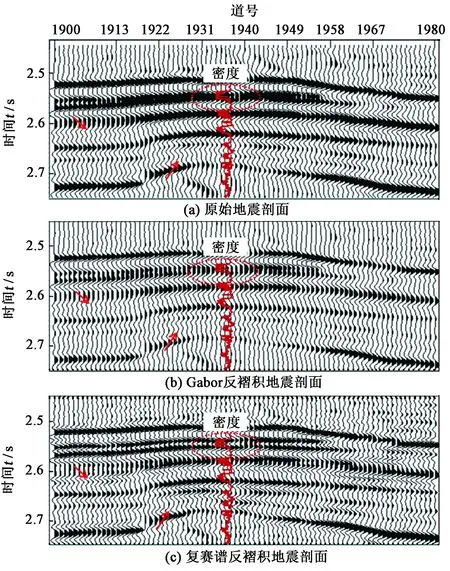
图8 反褶积前后剖面对比Fig.8 Comparison of profile before and after deconvolution
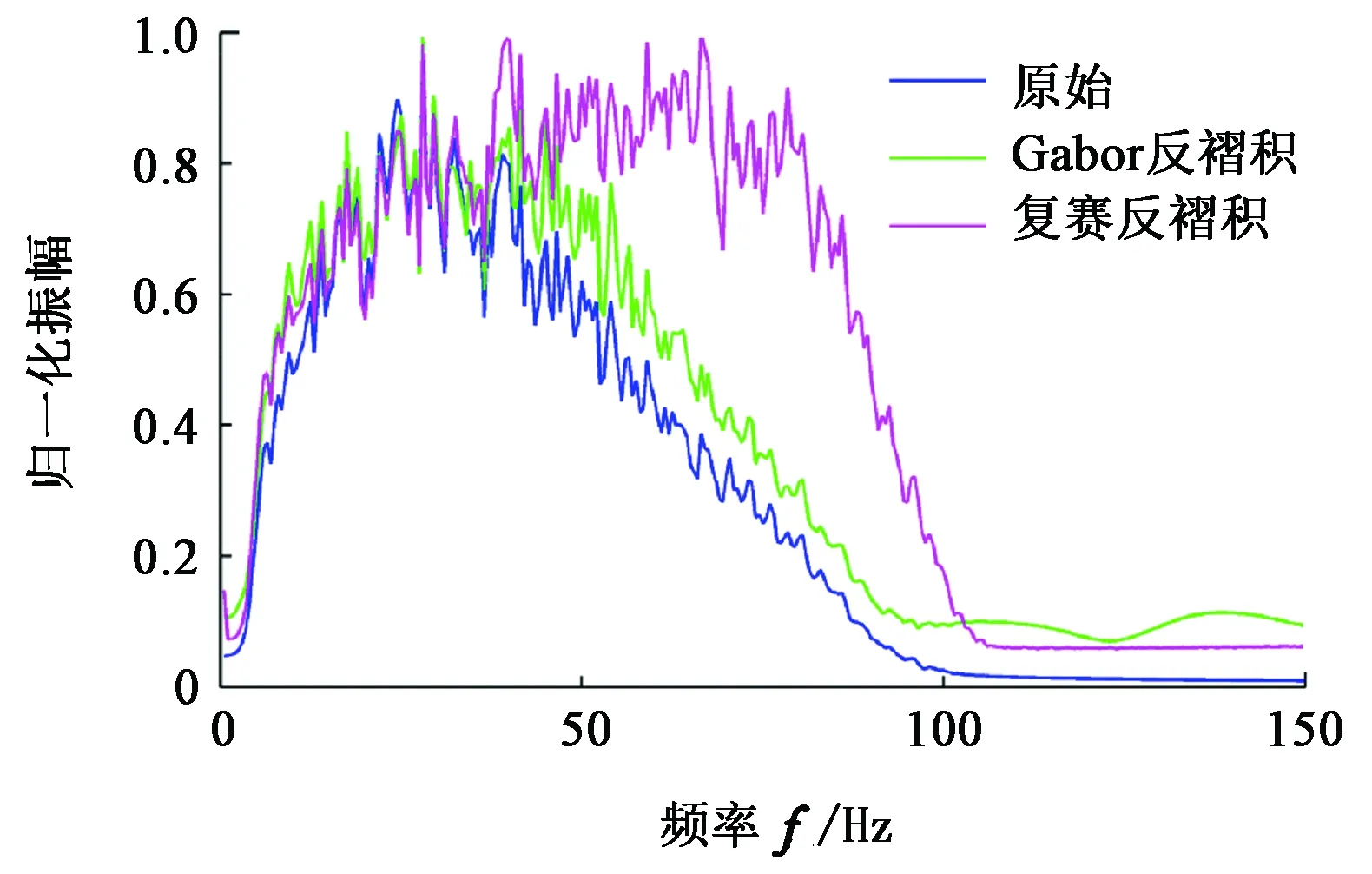
图9 反褶积前后剖面振幅谱对比Fig.9 Comparison of amplitude spectra before and after deconvolution
4 结 论
(1)本文中引入改进广义S变换,克服了傅里叶变换的时窗大小问题,弥补了Gabor变换时窗不能自适应频率变化的缺陷。
(2)在复赛谱时频域提取子波避免了反射系数白谱特性的假设,更加符合实际情况。
(3)改进后的算法更加稳定,能更好地恢复地层对地震波的衰减,同时提高了对薄储层的识别能力。
(4)地层对地震波的衰减是相对的过程,将反褶积扩展到复赛谱时频域后,每个时刻是相互独立的,因此不用考虑Q值的影响,直接恢复地震波的能量。
