债券市场投资中的非线性相关结构分析

范国斌 于翠婷 廖静池

(1.西南财经大学统计学院，四川 成都 611130；2.西南石油大学经济管理学院，四川 成都 610500；3.深圳证券交易所，广东 深圳 518038)

引言

股市常常动荡不安，即使进入21世纪以来，中国股市也已经历了三次较大的危机：2000～2001年，国有股减持计划导致股市大跌；2008年受全球金融危机影响，中国股市同样经历了很长时间的低迷；而从2015年下半年开始，股市再次遭受了迄今为止最为迅猛的熊市冲击，2016年首日开盘施行“熔断机制”，一日连续两次触发，直至今日股市仍在起伏。然而在股民深陷股市危机时，却很少有人选择投资其他市场进行风险分散化，尤其是成立已久的债券市场。Neftci等(2007)[8]指出中国股市散户投资者占多数，他们更倾向于在股市和银行存款之间调配自己资产，而很少同时参与股市和债市投资，债券市场上发挥主要角色的是机构类投资者。虽然由于经济制度、监管体制等因素的影响，中国债券市场的发展落后于股市，但金融理论早已证实，债券是相比股票更为安全的资产。而且Barsky(1989)[1]研究表明，股市和债市在金融风险时期会体现为负相关关系。当股市重挫时，投资者会抛售股票而购买风险更低的债券，并把这种行为称之为“安全投资转移(Flight-to-quality)”。对于深受股市风险困扰的中国投资者，正在不断发展和完善的债券市场能否成为其“避风港”？为此，本文试图对中国股市和债市间关系进行全面而科学的分析，以考察中国债券市场是否能为股市投资者提供一个风险分散化渠道。

进一步，当投资者考虑进入债券市场时，还必须注意债市中有很多不同的债券：从交易场所上讲有银行间债券和交易所债券，从期限上讲有长期债券和中短期债券，而从发行人上讲有国债、企业债和金融债。不同类型的债券和股市的关系可能会有所不同，而且投资者同时持有这些不同债券类型时，这些不同类型债券之间的相关关系同样值得考察。因此，除了股市与债市间关系外，本文也将对债市中不同类型债券间关系进行研究，从而帮助考虑进入债券市场的投资者制定合理的组合策略。

文献综述

对于股市和债市间关系，国外研究观点并不一致：Underwood(2009)[12]发现股市和债市间倾向于呈现为负相关关系，但Sellin(2001)[11]研究却认为，股票和债券会受到如货币政策等共同因素的影响而体现出正相关关系。然而后续的研究却进一步发现，事实上股市和债市间关系在不同的状态下会有所不同：Connolly等(2005)[2]发现，股市不确定性会导致股市与债市关联性改变，当股票市场不确定性加剧时，股市和债市会呈现负相关关系，从而使得分散化持有股票和债券能获得更大收益。Gonzalo和Olmo(2005)[4]也发现，当仅有股市面临危机时，股市与债市间存在安全投资转移行为，而当两个市场同时面临负冲击时，股市与债市之间会具有传染效应而体现为正相关。越来越多的研究表明，股市与债市间关系是会随着时间变化的(Yang等，2009)[13]。对于中国股市和债市间关系，现有研究也无一致结论：同样发现中国股市与债市间关系会随时间而变化(袁超等，2008)[18]。

在中国债券市场中，因交易场所、发行人以及期限的不同，存在很多类型的债券。大量研究表明，这些不同类型的债券可能会具有不同特征(巴曙松与姚飞，2013)[14]。因此，在考察股市与债市间关系时，有必要考虑到不同类型的债券可能会与股市间具有不同相关关系模式。同时，当投资者同时持有多种类型的债券时，还应考虑不同债券类型间的相关关系。然而现有研究却很少注意到这点，王璐和庞皓(2008)[16]曾分交易所和银行间债券市场来考察股市与债市间关系，而郑良海和侯英(2012)[19]曾考察了银行间债券市场和交易所债券市场间动态关系。除此之外，金融市场上投资者会因投资目的不同而选择不同的投资期限，所以无论考察股市与债市间关系时，还是考察不同债券类型间关系时，都有必要分不同频率的收益率进行全面分析。但现有文献中，只有闵晓平(2013)[15]曾经基于不同频率的数据对公司债市场的流动性进行了分析。

另外在分析上述相关关系时，必须注意到无论是股市与债市间关系，还是不同类型债券间关系，均有可能体现出非线性特征。大量研究表明，不同金融市场或不同金融资产之间的相关结构往往是非线性的，存在尾部相关性特征，也即极端情形下收益间相关程度会高于正常情形。因此，Copula函数作为一种更为灵活的工具，被广泛用来对这种非线性相关结构进行建模。Miller和Liu(2006)[7]等文献指出忽略了这种非线性相关结构特征会给投资者的资产配置绩效和组合风险管理带来极大损失。而Rodriguez(2007)[10]和Okimoto(2008)[9]又进一步发现不同市场或不同资产间相关结构不仅是非线性的，还有可能随时间变化。这一相关结构的时变性同样会影响投资者的组合策略(Fan和Zeng，2012)[3]，但目前只有肖利平(2011)[17]曾使用SJC-Copula对中国股市和债市间相关结构的非线性特征进行了分析。

鉴于现有研究的缺陷，本文旨在以下方面做出贡献。在研究角度方面：第一，鉴于现有研究对股市和债市之间的关系为正还是为负并无一致结论，本文考察中国股市和债市之间的关系究竟为何方向；第二，关于股市和债市间关系，存在不同理论。那么不同类型的债券便有可能体现出和股市不同的关系，而以往文献并未分析这一可能，因此本文除了股市和债市整体关系之外，进一步分析不同类型的债券与股市间关系是否不同；第三，如果投资者同时持有不同类型的债券，那么这些不同类型债券之间的相关关系也对组合绩效至关重要，因此本文还进一步考察不同类型债券之间的关系；第四，不同的投资者可能会选择不同的投资期限，因此与以往文献不同，本文基于三种不同频率的数据(日收益、周收益和月收益)考察股市与债市间相关结构以及不同债券类型间相关结构，分析不同频率下相关结构模式的可能不同。而在研究方法方面：使用灵活的Copula函数来对上述相关关系进行建模，以考察其相关结构是否具有非线性特征，并结合马尔科夫转换技术来进一步考察其非线性相关结构是否具有时变性。通过上述的科学分析，本文试图为投资者选择合理的债券产品构建其组合策略提供重要参考。

基于Copula的相关结构建模

一、Copula函数简介

Copula是一种可以将联合多元分布函数与各边际分布函数联系起来的连接函数。Copula理论中核心的Sklar’s定理指出：对于一个边际分布函数为F1,...,Fn的联合分布函数F，一定存在一个Copula函数使得F(x1,...,xn)=C(F1(x1),...,Fn(xn)),，其中边际分布的信息包含在Fi(xi)中，而变量之间的相关结构完全由Copula函数来刻画。这样我们可以先对边际分布做出任何假设，然后再选取不同的Copula函数来对相关结构单独建模。Copula可以度量非线性的相关结构，与线性的方差协方差矩阵不同，Copula函数允许处于分布中间和分布尾部的相关程度有所不同。特别地，特定的Copula函数可以捕捉到不同资产收益率之间的尾部相关性，即不同资产价格同时暴涨和暴跌的可能性大小。

不同的Copula函数代表着不同的相关结构模式，也对应有不同的尾部相关特征。本文首先选用文献中常用的4种Copula函数类型：Gaussian、T、Clayton和Gumbel。其中Gaussian Copula不存在尾部相关性(即不同资产价格暴涨或暴跌的情况是相互独立的)，常被作为基准模型使用；T Copula同时具有上尾和下尾相关性(即不同资产的价格既会同时暴涨又会同时暴跌)；不过这两种Copula函数所刻画的相关结构是对称的，而Clayton 和Gumbel Copula虽然可以度量非对称的相关结构，但前者只存在下尾相关性(即不同资产的价格仅可能同时暴跌但不会同时暴涨)，后者只存在上尾相关性(即不同资产的价格仅可能同时暴涨但不会同时暴跌)。

金融资产间的相关结构事实上是相当复杂的，有时很难用单一的Copula函数来进行刻画。当市场处于暴涨或暴跌时期，资产间相关性都会明显增强。而Clayton和Gumbel Copula只能捕捉到在下尾或下尾处一侧的尾部相关性，T Copula虽然在上尾和下尾处两侧都具有尾部相关性，但是其尾部相关性是对称的。可是在牛市和熊市时期的资产间相关性往往是非对称的，为了全面刻画股票与债券间以及不同债券间的相关结构，引入Hu(2006)[6]所提出的混合Copula的概念，构建一个Clayton和Gumbel Copula的线性组合。具体如下：

其中CCla和CGum分别指Clayton和Gumbel Copula函数，而πCla和πGum指这两种Copula函数对应的权重。这样构建的混合Copula相对比较灵活，同时存在上尾和下尾相关性，而且在上尾和下尾处两侧的尾部相关性程度是非对称的。首先同时使用单一Copula函数和混合Copula对静态相关结构进行全面的分析，然后进一步引入马尔可夫转换模型来考察相关结构的时变性。

二、马尔可夫转换模型的引入

为了考察资产间相关结构是否会在不同的时期有所不同，参照Rodriguez(2007)[10]和Okimoto(2008)[9]的做法，本文同样将Copula函数与马尔可夫模型结合起来对相关结构进行建模。首先，尝试令不同资产间的相关结构服从一个两状态马尔可夫转换过程，在不同的状态下，相关结构由不同的Copula函数来刻画，具体设定如下：

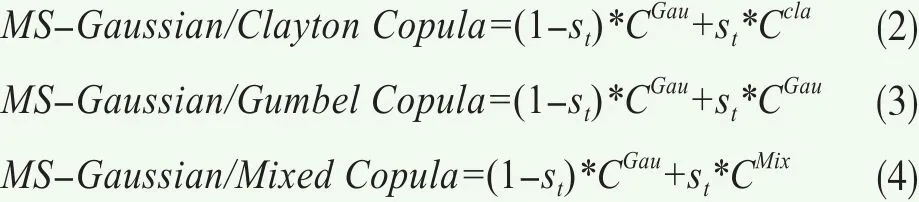
其中Ci,i∈{Gau,Cla,Gum,Mix}分别指前文给出的各类单一Copula函数以及混合Copula。由于在市场暴跌或暴涨时期，不同市场或不同资产之间的相关程度可能会变得比市场平静时期更强，因此在上述3种马尔可夫转换Copula设定中，均将市场状态设置为两状态。其中状态一为市场平静状态(st=0)，此时变量间相关结构由不存在尾部相关性的Gaussian Copula来刻画；而状态二为市场动荡状态(st=1)，此时变量间相关结构由Clayton、Gumbel 或混合Copula来刻画，这三种非对称的Copula来刻画均能够捕捉在市场暴跌或暴涨时可能出现的非对称尾部相关性特征。除此之外，本文还尝试引入了第四种设定“MS-T Copula”，允许T Copula的自由度参数依状态进行转换。与前面三种设定类似地，将市场状态设置为两状态，状态一((st=0))和状态二((st=01)分别对应市场平静时期和市场动荡时期。其中在状态一下，T Copula的自由度参数变大，从而使得T Copula事实上已经退化为Gaussian Copula，尾部相关性会变得消失；在状态二下，T Copula的自由度参数相对较小，因此可以捕捉市场暴跌或暴涨时可能出现的尾部相关性特征。在四种不同的设定中，均令状态 的变化服从一个马尔可夫链，其状态转移矩阵为

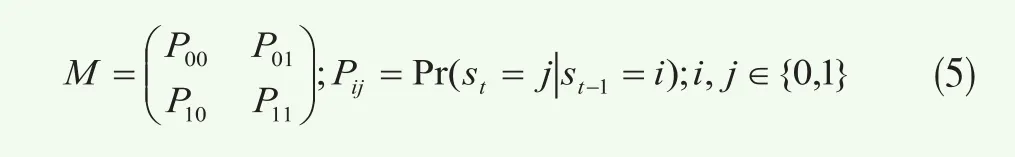
这种将马尔可夫转换和Copula函数结合起来研究资产间相关结构的方法可以使得不同的时期相关结构发生变化，而不仅仅是同一种相关结构的相关程度的变化，本文把这种方法称之为“马尔可夫转换Copula”。

对于马尔可夫转换Copula模型的估计，首先在每一时刻t可以计算得到基于不同状态和以往收益的条件密度函数：

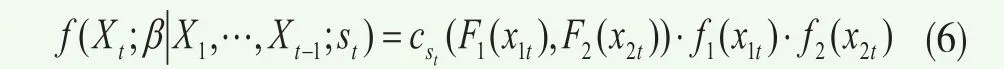
其中 为在时刻t的观测值，β表示需要估计的参数，cs所对应的Copula函数类型取决于不可观测的状态st。然后可以按照Hamilton(1994)[5]给出的循环程序得到不再依赖于状态的无条件密度函数，并最后写出似然函数:试公式(2)～(4)所设定的三种马尔科夫转换Copula形式；如果最优Copula函数为对称的T Copula，那么尝试第四种马尔科夫转换Copula形式“MS-T Copula”。通过对比马尔科夫转换Copula形式与静态Copula的AIC值，以及观察马尔科夫转换Copula形式下相关结构是否会在不同状态下有所不同，从而分析上述相关结构是否会存在时变性特征。

实证结果与分析

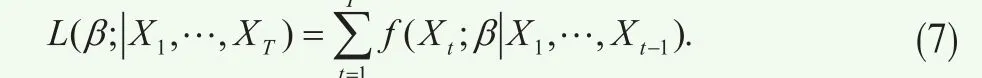
得到上面的似然函数之后，采用极大似然估计就可以得到模型参数值。

基于以上方法，本文对股票和债券间相关结构以及不同债券间相关结构进行分析，并将所有资产的边际分布均设定为经验分布形式。首先根据AIC准则选取最优的静态Copula函数类型，然后基于最优Copula函数进一步考察可能的时变性特征：如果最优Copula函数为非对称的Copula类型(Clayton、Gumbel或Mixed Copula)，那么尝

为了考察股市和债市之间的相关结构，本文搜集了上证综合指数、深证成份股指数和中债总指数，样本区间为2012年1月4日～2015年12月31日。除了股市和债市间整体关系的分析外，进一步搜集了债券市场上不同类型债券指数的数据：交易所债券与银行间债券指数(按交易场所不同)，中短期债券与长期债券指数(按偿还期限不同)，国债、企业债和金融债指数(按发行人不同)。进而，分析上述每一类型债券与股市间的相关结构以及不同债券类型之间的相关结构，由于分类债券指数数据起始日期较晚，因此涉及到分类债券指数的相关结构分析样本区间为2006年11月21日～2015年12月31日。本文分别计算了上述指数的日收益、周收益和月收益，对比分析不同频率下的相关结构特征，所有收益率均基于收盘价计算为对数收益率。

一、股市与债市间相关结构

由于股市和债市间关系为正还是为负并不明确，因此在考察两者关系时，分别尝试了对股票收益率与债券收益率直接进行Copula建模和对股票收益率和债券收益率的相反数间关系进行Copula建模，对比其AIC值发现，后者拟合程度明显更高。因此，本文选择将股票收益率和债券收益率的相反数间相关结构的估计结果以表1～3给出，其中符号为正的相关系数(ρ)或尾部相关系数(λU和λL分别代表上尾和下尾相关性系数)代表着股市和债市间存在负向关系。除了股市和整个债市间相关结构外，还给出了股票和不同类型债券间的相关结构，表1～3分别为基于日收益、周收益和月收益的结果。从中可以看出：

首先，虽然对于日收益率，股市和债市间相关关系较弱，但对于周收益和月收益，无论是股市和整个债市间还是股市和不同分类债券间，均存在不可忽略的负相关关系，而且频率越低，负相关程度越强。这至少对于投资期限较长的投资者来说是个好消息，股票和债券之间的负相关关系意味着中国债券市场确实能够对股市风险起到一定的分散化作用。这一发现也可能表明中国金融市场上也存在一定的“安全投资转移”现象，即在股市风险较大时，投资者会转而购买风险更低的债券，从而使得股市和债市体现出一定的负相关关系。只是因为通常投资者调整其资产组合的频率相对较低，所以这种负相关关系只在周收益和月收益间体现，而在日收益间并不明显。

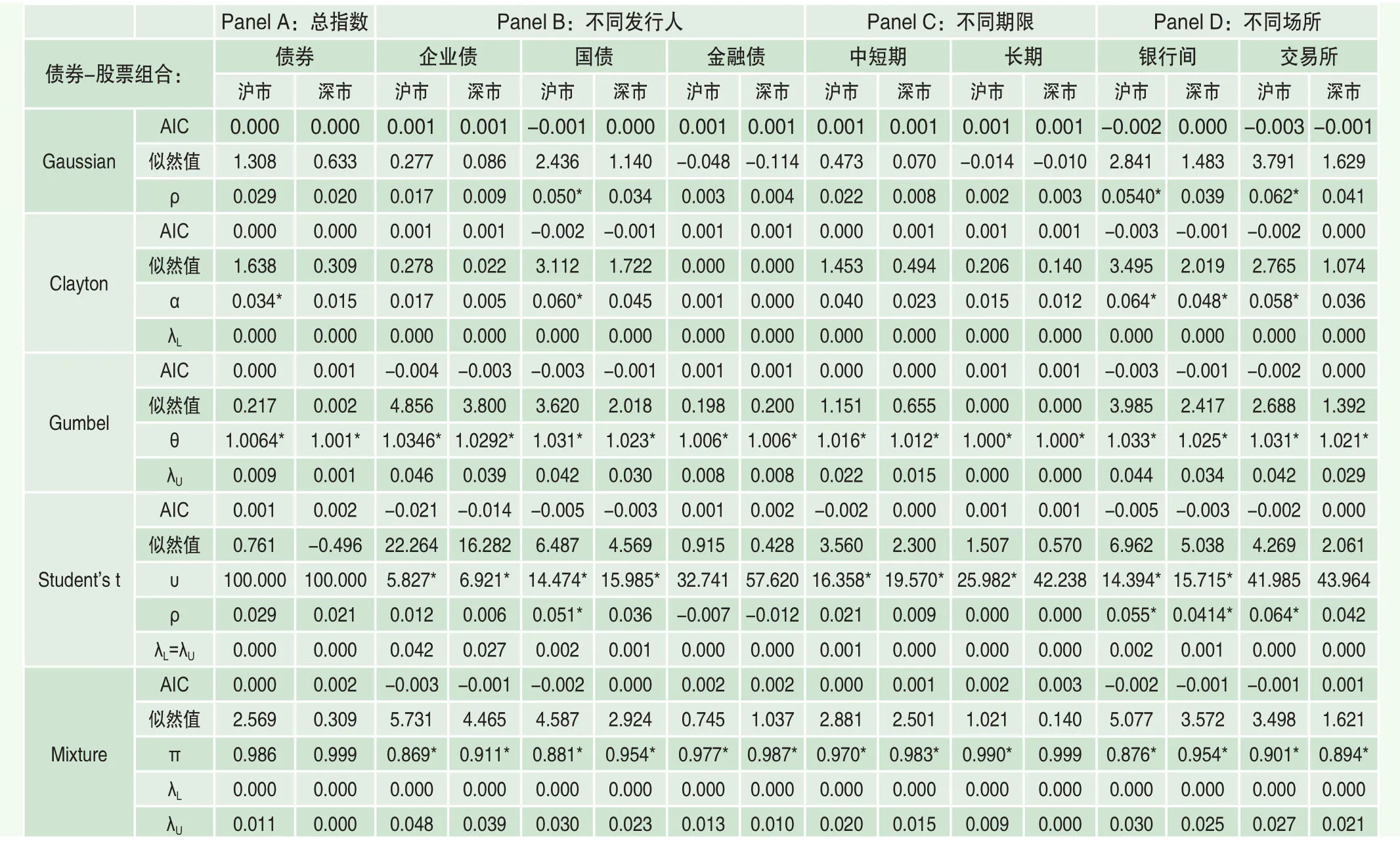
表1 基于日收益的中国股市与债市间相关结构分析

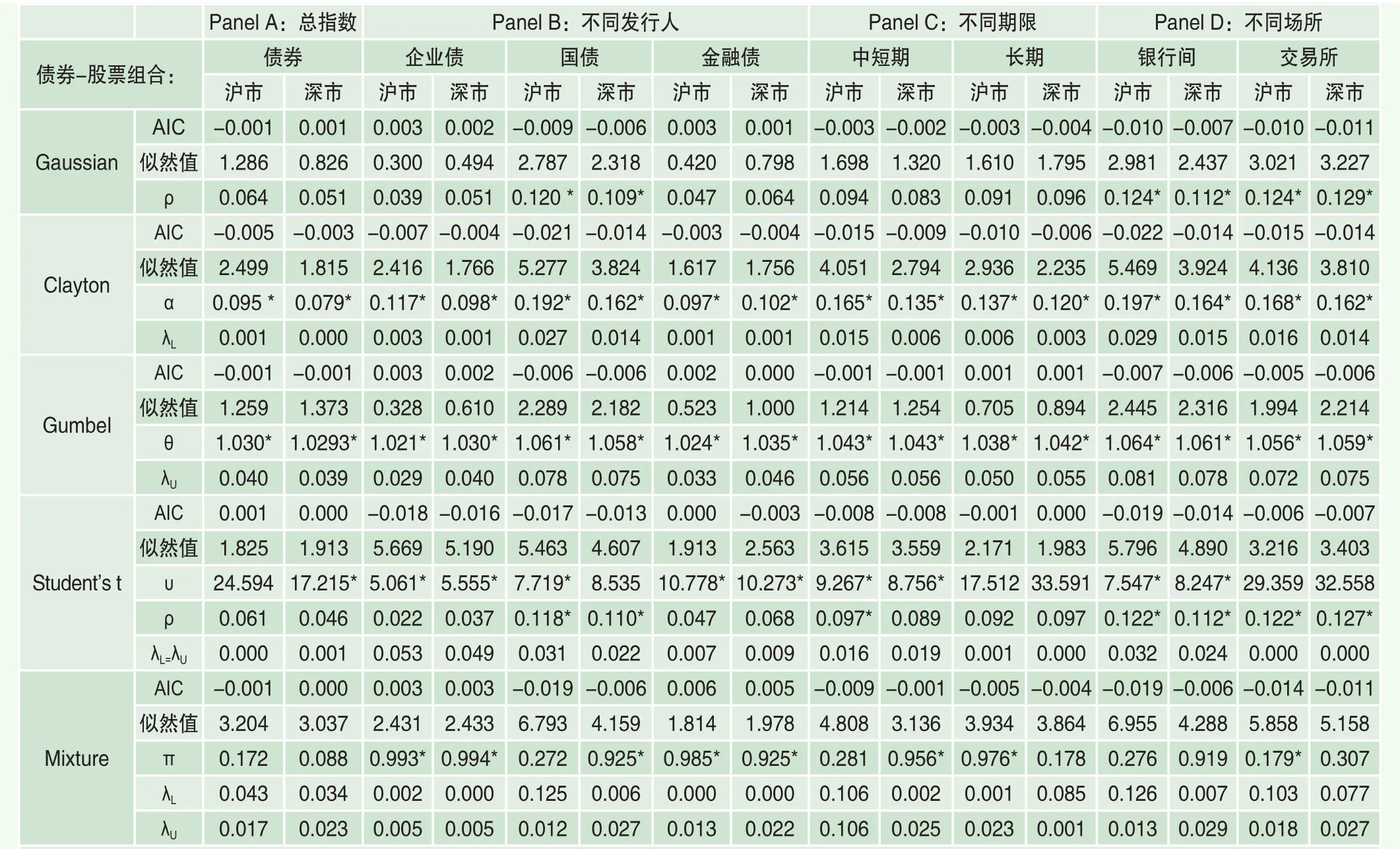
表2 基于周收益的中国股市与债市间相关结构分析

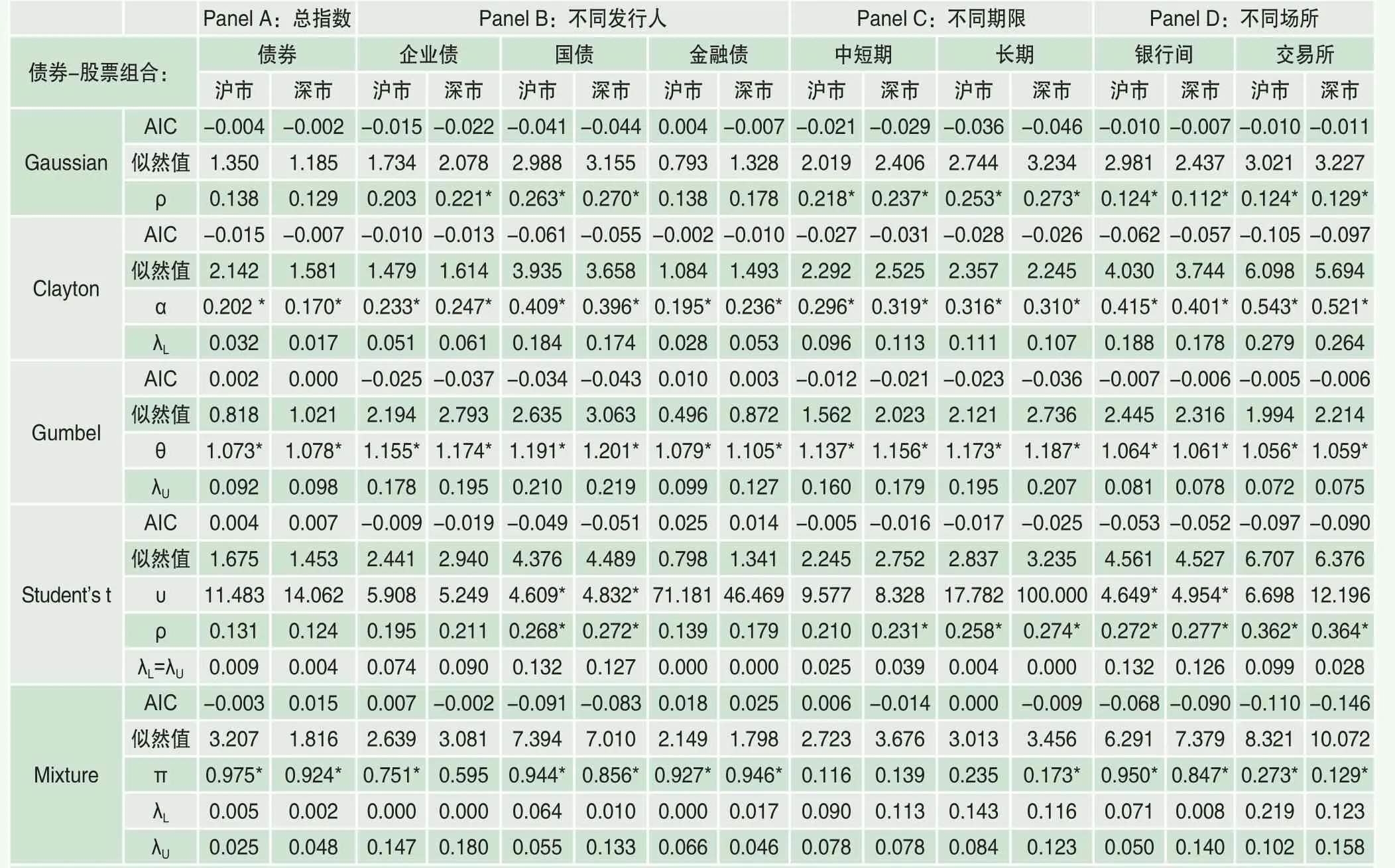
表3 基于月收益的中国股市与债市间相关结构分析

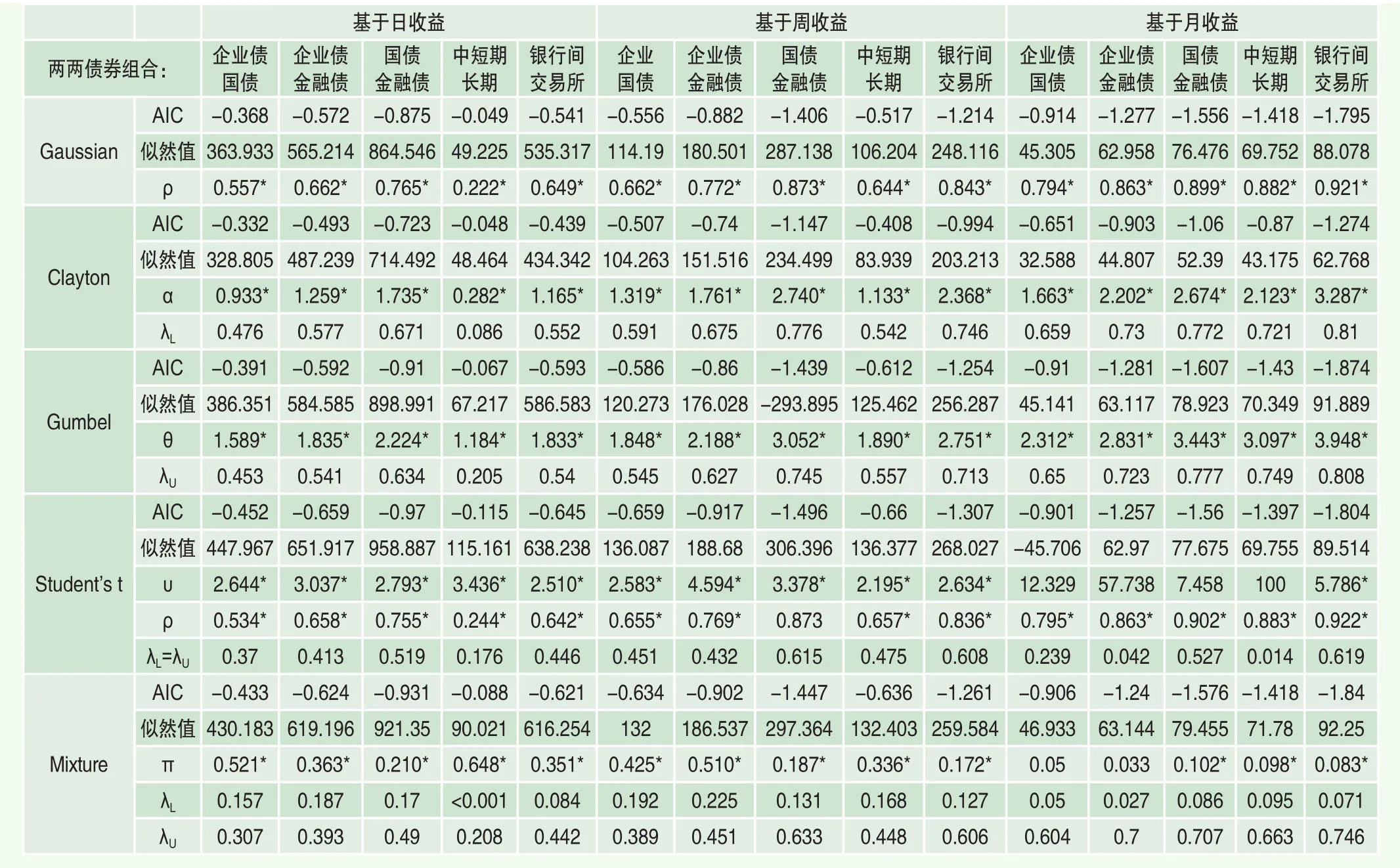
表4 不同类型债券间相关结构分析

而且，不同频率下的相关结构均明显体现出尾部相关性特征，刻画日收益间相关结构的最优类型为T Copula，刻画周收益间相关结构的最优类型为Clayton Copula，而刻画月收益间相关结构的最优类型为Clayton Copula或Mixed Copula。前文已指出，这种尾部相关性特征意味着，当市场处于暴涨或暴跌时期，两项资产之间的相关程度会变得相对更强。而且三种频率下的最优Copula函数类型均具有下尾相关性，对于本文来说，下尾对应于股市收益率下降的时候。也就是说，当股市收益率下降时，股市和债市间负相关程度会更强，这提示我们，在股市暴跌时期，债券市场对股市风险的对冲作用更为明显。

进一步对比不同类型债券与股票间相关关系则显示，在发行人不同的债券中，企业债和股市的相关程度最强，三种频率下结果均如此；在偿付期限不同的债券中，对于日收益和周收益，中短期债券与股市间相关程度更高，而对于月收益，长期债券与股市间相关程度更强；在交易场所不同的债券中，银行间债券和交易所债券与股市间的相关程度并无一致结论。此外，对比沪市和深市两个市场与债券间相关程度时表明，对于日收益和周收益，沪市体现出更强的与债市间相关关系，然而对于月收益，深市与债市间相关程度却强于沪市。

二、不同类型债券间相关结构

当投资者进入债券市场时，有多种不同类型的债券可供其选择，而不同类型债券间的相关结构也对其组合策略至关重要。因此，本文对三种划分准则下的不同债券间的两两相关结构进行分析，并将估计结果在表4中给出。与表1～3的结果不同，此处是对两种债券的收益率间关系直接进行Copula建模(并未取相反数)。首先，从结果中可以看出：与股市和债市间相对较弱的负相关关系不同，不同债券之间表现出很强的正相关关系，而且随着频率降低，不同债券之间的正向相关程度越来越强。这意味着，当在一个组合中同时持有多种债券类型时，必须注意其收益率会更倾向于同向变化而很难发挥风险分散化的作用。而且，三种频率下的相关结构均存在着明显的尾部相关性特征，也就是说，对于不同债券类型间关系，也会同样在市场暴涨或暴跌时表现出相比平静时期更强的相关程度，因此使得我们在最需要分散风险的时候却很难通过持有不同债券类型来实现目的。

对比不同频率下结果可以发现，对于日收益和周收益来说，刻画不同类型债券间相关结构最优的函数是T Copula，说明同时存在着对称的上尾和下尾相关性，也即无论在市场暴涨还是暴跌时期，不同债券的收益率相关性均会有所增加。而对于月收益来说，刻画不同类型债券间相关结构最优的函数是Gumbel Copula，该函数仅存在有上尾相关性。这意味着，对于持有债券期限较长的投资者来说，不同类型债券的收益率更倾向于在市场好转的时候体现出更高的相关程度。

三、相关结构的时变性特征

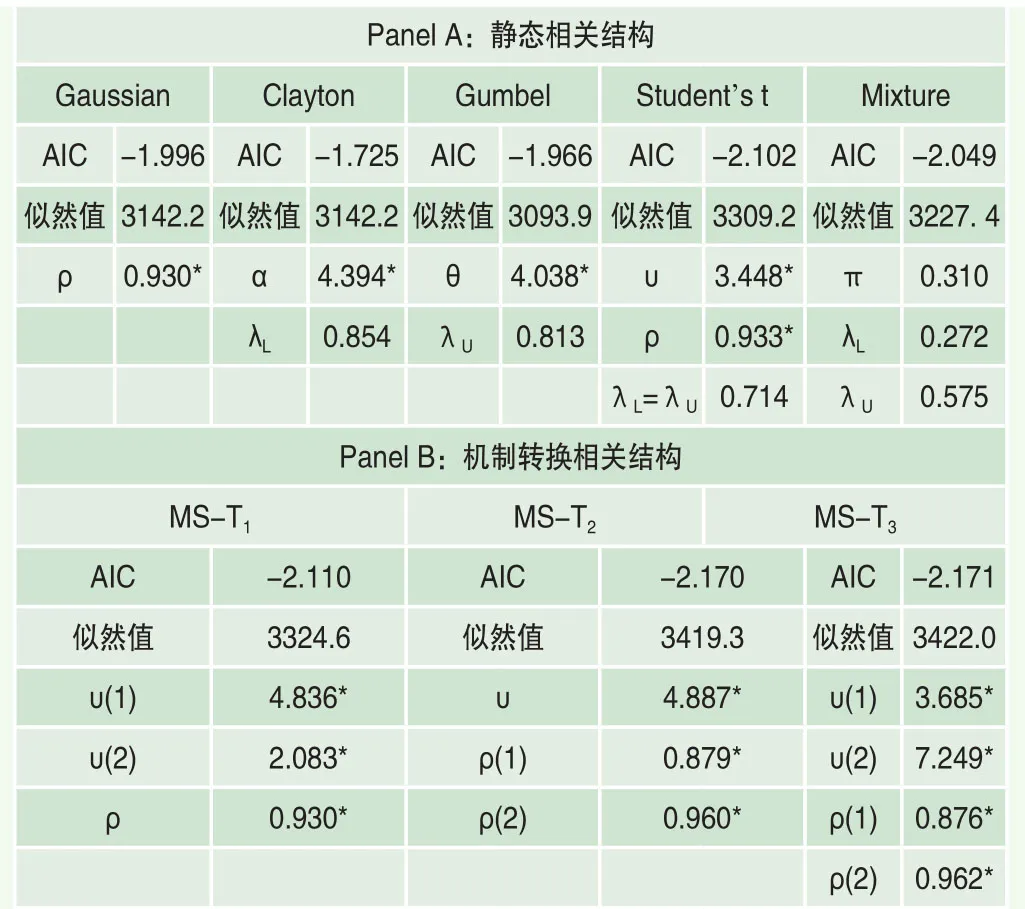
表5 沪深两市间相关结构及其时变性特征分析(基于日收益)

大量文献表明，金融市场或金融资产间相关结构不仅是非线性的，而且还有可能是时变的。如果对沪深两个股市间相关结构进行分析，可以发现虽然其静态相关结构最优的仍然为T Copula，但进一步引入马尔科夫转换机制后发现，其相关结构会随时间发生明显变化。由于最优的静态相关结构为T Copula，所以选择第四种马尔科夫转换Copula设定形式“MS-T Copula”，分别尝试只让T Copula的自由度参数依机制转换、只让T Copula的相关系数参数依机制转换、让T Copula的自由度参数和相关系数参数同时依机制转换，在表5中将其标记为“MST1”，“MS-T2”和“MS-T3”。基于AIC准则对比发现，马尔科夫转换Copula设定的拟合程度明显优于静态Copula，其中最优形式“MS-T3”的参数估计结果显示，两个股市间的相关系数和自由度参数会在不同状态下有所不同。

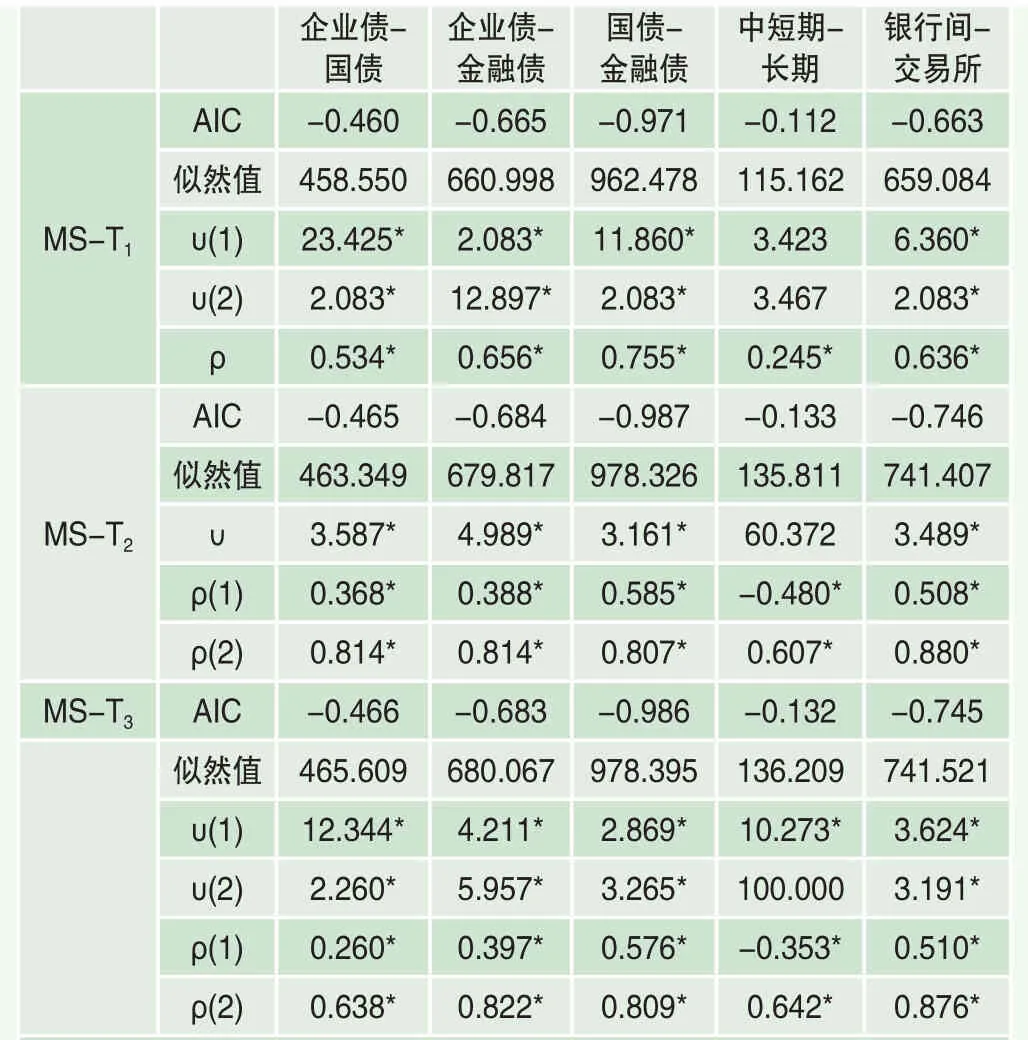
表6 不同类型债券间相关结构的时变性特征分析(基于日收益)

因此，对于股市和债市之间相关结构以及不同类型债券之间的相关结构，同样有必要进一步引入马尔科夫转换技术考察其相关结构可能的时变性。对于股市和债市间相关结构，可能因为其相关程度较弱，尝试了本文所设定的四种不同马尔科夫转换Copula形式，均未发现存在时变性特征。然而对于债券市场上不同类型的债券之间相关结构，却可以发现存在明显的时变性特征。由于表4结果显示，不同类型债券之间最优的静态相关结构T Copula，所以同样选择“MS-T Copula”的设定形式，与表5中结果类似，分别尝试了“MS-T1”，“MS-T2”和“MS-T3”三种情况。同样地，表6的结果告诉我们，马尔科夫转换Copula设定形式的拟合程度明显优于静态Copula，其中最优的形式为“MS-T2”。也就是说，不同类型债券间相关结构具有时变性特征，其相关系数会在不同状态下有所不同。

结论

随着中国金融市场的不断健全和完善，投资者应该与时俱进，不再只局限于股市，而应该考虑投资于不同市场以主动进行风险分散化。尤其是当股市风险较大的时候，应考虑选择相对更为安全的资产，例如债券。然而，债市究竟能否成为股市的“避风港”以及投资于债市时应选择哪些类型的债券？为回答这些问题，本文对中国股市与债市间和债市中不同类型债券间非线性相关结构进行了全面分析，并得到如下结论：中国债券市场能够为股市提供一定的风险对冲作用，尤其是对于周收益和月收益，债市和股市间存在较强的负相关关系。这说明至少对于投资期限较长的投资者来说，可以通过持有债券来分散化股市风险；在不同类型的债券中，企业债和股市间的负相关关系相对较强，因此企业债可能是对冲股市风险的最佳选择；其他债券类型和股市间关系强弱程度则无明显差异，而且债市中不同类型债券间关系显著为正，因此投资者在考虑持有债券时，没有必要同时持有多种不同类型的债券，可能并不会为风险分散化带来进一步的帮助；此外，债市和股市间相关结构具有明显的尾部相关性特征，也即在股市下跌时，两者间负相关程度更强，因此同时持有股票和债券的风险分散化效果将更为明显；最后，债市中不同类型债券间相关结构不仅同样为非线性，而且还会进一步体现出时变性特征。具体而言，在市场动荡状态下，不同债券之间会表现出明显的尾部相关性，其正向相关关系的程度将变得更强。这再次提示投资者，在试图通过持有债券来对冲股市风险时，选择同时持有多种债券的意义不大。

所有这些结论对于试图进入债券市场的投资者来说具有重要参考价值：首先，这意味着投资者确实可以选择通过债市来分散股市风险。但是，同时持有多种不同类型债券时却要注意它们之间的收益往往会同向变化，要合理控制自己的组合风险。另外，股市和债市间相关结构和不同类型债券间相关结构均具有非线性特征，而且不同类型债券间相关结构还进一步具有时变性特征，考虑到这两种特征将能给投资者的资产配置绩效和组合风险管理带来明显的改进。