聚氯乙烯涂层膜材料非线性蠕变性能预测
2018-10-30汪泽幸周锦涛李洪登
汪泽幸, 刘 超, 何 斌, 周锦涛, 李洪登
(1.湖南工程学院 纺织服装学院, 湖南 湘潭 411104; 2.湖南省新型纤维面料及加工工程技术研究中心, 湖南 益阳 413000)
膜材料通常承受张拉载荷作用,与索、缆及其他建筑材料构成一体,形成并长期保持其复杂的外观形态[1]。作为一种典型的黏弹性材料,在张拉载荷作用下,膜材料将表现出蠕变特性,从而产生复杂的形态变化,对其长期使用性能和安全性能产生较大的影响[2-3],因而需对膜材料的蠕变性能做深入的研究,为膜材料的加工和使用、膜结构的设计和施工提供参考依据。
对于以织物增强类膜材料为代表的黏弹性材料,研究蠕变性能时,一般采用经验模型法、数值分析法和物理模型法等。基于经验公式的经验模型法在描述材料的蠕变特性时,物理意义不明确;数值分析法是基于膜材料微观物理模型的构建和分析获得的各项力学参数,但模型参数较多且难以确定;物理模型法基于虎克弹簧和牛顿黏壶构建黏弹性模型,以经典且简单的Maxwell模型和Kelvin模型为代表。将经典黏弹性模型扩展,可获得广义Maxwell模型和广义Kelvin模型,随着基本元件数量的增加,拟合的精度提高[4],但计算繁杂。
传统的元件组合模型中,蠕变参数为常数,无法反映黏弹性材料的非线性蠕变特性。为描述非线性蠕变特性,Schiessel等[5]建立的分数阶Maxwell和分数阶Kelvin模型,可较好地模拟聚四氟乙烯(PTFE)膜材料的蠕变和松弛性能[3]。康永刚等[6]采用黏滞系数为应变速率幂函数的非线性黏滞体,建立了修正P-T(Poynting-Thomson)模型,并验证了该模型的可行性。
目前,对黏弹性材料长期蠕变性能预测时,主要有时间-温度或时间-应力-温度等效原理法、经验公式法和元件模型法等。高温、高应力条件下的加速蠕变测试会导致材料失效机制变化,导致预测与实测结果有较大出入[7]。经验公式法无明确的物理意义;而物理模型不仅物理意义明确,且理论推导明确,其中,Burgers模型理论推导较为成熟,简单直观,应用方便,虽实验已验证其描述黏弹性材料蠕变性能的合理性[8-10],但因其基于线性黏弹性元件而构建,所以在非线性黏弹性材料长期蠕变寿命预测时的精度较差[8-9]。
本文基于聚氯乙烯(PVC)涂层膜材料,采用非线性黏滞体替代Burgers模型中Maxwell单元的线性牛顿黏壶,从而构建修正Burgers模型,并讨论模型的适用性。
1 实验材料与方法
1.1 实验材料
以商购施恩特膜材料为研究对象,其表层涂覆耐气候层聚偏氟乙烯(PVDF)的PVC涂层膜材料,织物组织为2上2下方平组织,经纬纱均为111.1 tex/192 f高强涤纶长丝,经纬向密度均为24根/(5 cm),膜材料厚度为0.72 mm,面密度为800 g/m2。
1.2 试样制备与实验方法
所有蠕变实验均参考FZ/T 60037—2013《膜结构用涂层织物 拉伸蠕变性能试验方法》,采用WDW-20C型微机控制电子试验机进行测试,矩形试样长为300 mm、宽为50 mm,有效夹持隔距为200 mm,试样夹持部位均采用高强黏合剂黏合铝合金薄片加以保护。
设定蠕变应力为10、15和20 N/mm,以 100 mm/min的加载速率拉伸试样,蠕变时间为48 h。有效试样样本数为3,以具有代表性蠕变曲线为后续分析对象。
2 结果与分析
图1示出试样在蠕变应力为10、15、20 N/mm条件下经48 h(2 880 min)后的经纬向蠕变曲线。可以看出,膜材料在不同载荷作用下的应变由加载过程产生的瞬时应变、衰减蠕变应变和稳态蠕变应变3部分构成。所施加的最高应力未达到使膜材料发生加速蠕变的临界应力,且蠕变时间较短,经纬向试样均未出现加速蠕变阶段。

图1 试样的蠕变曲线Fig.1 Creep curves tested specimens.(a) Warp specimens; (b) Weft specimens
由图1还可看出,在不同蠕变应力下经纬向试样蠕变曲线形态具有一致性,说明经纬向试样的蠕变机制相同。对于经、纬向试样而言:均表现出瞬时应变和蠕变应变随蠕变应力增加而增加的变化趋势;相对于经向试样,同等蠕变应力条件下,纬向试样的瞬时应变和蠕变应变较高。根据蠕变实测数据可获得等时应力-应变曲线。
图2示出试样经向的等时应力-应变曲线。可见,不同时刻的等时应力-应变曲线形状存在明显的差异。蠕变时间为0时,等时应力-应变曲线向应变轴弯曲,且蠕变应力小于15 N/mm时,近似为直线,可认为PVC涂层膜材料经向在蠕变应力低于15 N/mm时,瞬时应变以弹性应变为主。随着蠕变时间流逝,等时应力-应变曲线向应变轴弯曲的程度越明显。由此可见,PVC涂层膜材料的蠕变具有非线性特性,其非线性程度与蠕变时间和蠕变应力相关,蠕变时间越长,蠕变应力越高,非线性程度越高。

图2 试样经向等时应力-应变曲线Fig.2 Isochronous stress-strain curves of warp specimens
3 蠕变模型
3.1 Burgers模型
常用的四元件Burgers模型由Maxwell单元和Kelvin单元串联组成,见图3。图中EM、EK为元件1和元件3的弹性模量,N/mm;ηM、ηK为元件2和元件4的黏滞系数,N·min/mm。

图3 Burgers模型Fig.3 Burgers model
蠕变应力为σ0时,蠕变应变及蠕变速率的表达式为:
(1)
(2)
式(1)可简化表示为
εB(t)=AB-BBexp(-t/τk)+CBt
(3)
式中:t为蠕变时间,min,AB=σ0/(EM+EK);BB=σ0/EK;CB=σ0/ηM;τk=ηK/EK,为Kelvin单元的推迟时间,min。
3.2 修正Burgers模型
由前述分析可知,PVC涂层膜材料蠕变的非线性程度与蠕变时间和蠕变应力相关,因而可引入非线性黏滞体替代线性黏滞体(见图3中元件2),建立修正Burgers模型。
目前常用的非线性黏滞体有分数阶导数单元的Abel黏壶及黏滞系数为蠕变时间函数的非线性黏滞体2类。
Abel黏壶的本构方程[3]为
(4)

当应力σ为蠕变应力σ0时,该元件将描述黏弹性行为的蠕变,其蠕变应变εAbel(t)为
(5)
式中,Г(1+a)为 Gamma函数。
对于黏弹性材料的衰减蠕变和稳态蠕变阶段,黏滞系数将随蠕变时间的增加而发生硬化[8],可引入黏滞系数为蠕变时间的单调递增函数的非线性黏滞体,以此构建非线性黏弹性模型。
李猛[11]认为非线性黏滞体的黏滞系数与蠕变时间的变化关系可用幂函数表示,该非线性黏滞体的黏滞系数ηP(t)可表示为
(6)
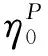
外加应力为σ时,其本构方程为
(7)
蠕变应力为σ0时,蠕变应变εP(t)可表示为
(8)
式(5)与式(8)的表达形式一致,因而可认为幂函数型的非线性黏滞体与Abel黏壶在表达蠕变时是等效的。
用Abel黏壶替换Burgers模型中的元件2,可得分数阶导数单元修正Burgers模型,简称分数阶Burgers模型(MF-Burgers模型),其蠕变方程可表示为
(9)
式(9)可简化为
εMF(t)=AMF+BMFexp(-t/τk)+CMFta
(10)
式中:AMF=σ0/(EM+EK);BMF=σ0/EK;CMF=σ0/[η0Г(1+a)]。
张久鹏等[12]认为非线性黏滞体的黏滞系数ηE(t)与蠕变时间的关系可用指数函数来表示,即
(11)

将式(11)对时间t求导并整理,可得
(12)

蠕变应力为σ0时,其蠕变应变εE(t)可表示为
(13)
式(13)与Kelvin模型的蠕变应变表达形式一致,可认为该非线性黏滞体在描述蠕变时,与Kelvin模型是等效的。
采用ηE(t)=peqt的黏滞体替代Burgers模型中元件2,可得指数型修正Burgers模型(简称ME- Burgers模型),其蠕变应变εME(t)表达式为
(14)
因该非线性黏滞体在描述蠕变时与Kelvin模型等效,故可认为ME-Burgers模型与1个Maxwell单元和2个Kelvin单元相串联而构建的物理模型是等效的,故MF-Burgers模型本质上仍是线性模型。
同理,式(14)可简化为
εME(t)=AME+BMEexp(-t/τk)+CMEexp(-qt)
(15)
式中:AME=σ/(EM+EK+pq);BME=BB=σ/EK;CME=σ/pq。
3.3 Findley幂函数模型
在描述黏弹性材料的蠕变性能的众多经验模型中, Findley等提出了应用最为广泛的幂函数模型,其蠕变应变εF(t)可表示为
εF=AFtr+ε0
(16)
式中:ε0为初始蠕变应变,mm/mm;AF、r为与蠕变应力及蠕变时间相关的变量。
4 模型参数识别与蠕变性能预测
4.1 蠕变模型参数识别
基于上述4种蠕变模型的简化表达式,对实测蠕变数据进行拟合分析,结果见图4~7。拟合时,需小心赋予初值,以免出现拟合不收敛现象的出现。

图4 Burgers模型蠕变曲线Fig.4 Creep curves of Burgers model.(a) Warp specimens; (b) Weft specimens

图5 MF-Burgers模型蠕变曲线Fig.5 Creep curves of MF-Burgers model.(a) Warp specimens; (b) Weft specimens

图6 ME-Burgers模型蠕变曲线Fig.6 Creep curves of ME-Burgers model.(a) Warp direction; (b) Weft direction
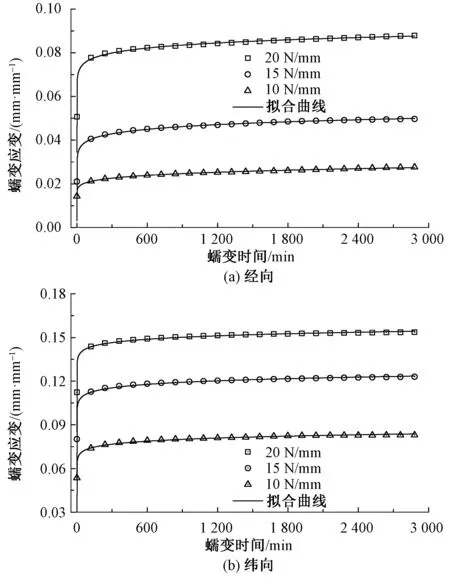
图7 Findley幂函数模型蠕变曲线Fig.7 Creep curves of Findley power law model.(a) Warp specimens; (b) Weft specimens
本文选用的4种蠕变模型均具有较好的拟合精度,均可描述PVC涂层膜材料的蠕变特性,其中MF-Burgers模型的拟合精度最佳。从图中还可看出,蠕变曲线拐点附近即蠕变初始段,实验值与计算值之间存在偏差,但随着蠕变时间的推移,偏差逐渐减少,直至可以忽略不计。
4.2 蠕变性能预测
基于上述4种蠕变模型的简化表达式,对前 12 h的蠕变实测数据进行拟合分析,并基于获得的蠕变模型拟合参数对48 h的蠕变性能进行预测,预测结果见图8。

图8 蠕变应变拟合及预测结果Fig.8 Simulation and prediction results of creep strain.(a) Warp direction;(b) Weft direction
由图8可知:Burgers模型和ME-Burgers模型的预测值随蠕变时间的增加而逐渐偏离实测值;预测时间越长,Burgers模型的预测值呈现直线状偏离实测值,且高于实测值,而ME-Burgers模型的预测值小于实测值;Findley幂函数模型和MF-Burgers模型的预测值与实测值之间的吻合度均较好,其中MF-Burgers模型的预测值最接近实测值,表现出最佳的预测精度。这是因为在蠕变应力作用下,随着蠕变时间的增加,材料内部结构发生复杂的变化,材料变形表现出强烈的时间依赖性,黏滞系数随蠕变时间的增加而发生硬化[8],用Burgers模型预测蠕变性能时,蠕变速率近似为常数并主要取决于ηM[8],因而基于常数ηM建立的Burgers模型,虽可用于描述实测范围内的蠕变性能,但长期蠕变性能的预测精度较差。ME-Burgers模型虽采用基于非线性黏滞体而构建,但其本质上仍为线性物理模型,不能用于非线性蠕变性能的预测。而MF-Burgers模型为采用非线性黏滞体构建的非线性物理模型,且可反映黏滞系数硬化现象,因而可较好地拟合实测蠕变数据,且蠕变预测精度较好。而对于Findley幂函数模型,虽无明确物理意义,但其表现出较好的拟合和预测精度,可用于非线性蠕变特性黏弹性材料蠕变性能的预测[8, 12]。
5 结 论
本文采用Burgers模型及其修正模型对PVC涂层膜材料在室温条件下的蠕变性能进行了拟合和预测分析,得到以下结论。
1)随着蠕变应力的增加,PVC涂层膜材料的瞬时应变、蠕变应变均随之增加。同等蠕变应力条件下,相对于经向试样,纬向试样的瞬时应变和蠕变应变较高。
2)等时应力-应变曲线表明,PVC涂层膜材料的蠕变具有非线性特征,非线性程度与蠕变时间和蠕变应力相关,蠕变时间越长,蠕变应力越高,非线性程度越高。
3)Burgers模型、基于非线性黏滞体建立的修正Burgers模型及Findley幂函数模型均可用于描述PVC涂层膜材料的蠕变性能,但蠕变性能预测时,分数阶Burgers(MF-Burgers)模型的预测精度最佳且物理意义明确,Findley幂函数模型次之,指数Burgers(ME-Burgers)模型再次之,Burgers模型的预测精度最差。
因实验条件的限制,本文选用的蠕变时间相对较短,MF-Burgers的长时间蠕变的预测精度及其对其他织物类涂层膜材料的适用性,仍需做进一步的研究。
