一类三圈连接图TK关于Hosoya指标的排序

尚娅璇，田文文

(1.中南林业科技大学 材料科学与工程学院, 湖南 长沙 410004;2.西安交通大学 机械工程学院, 陕西 西安 710049)

0 引言

Hosoya指标是由日本化学家Haruo Hosoya于1971年在文献[1]中提出并进行研究的, 它表示图G中所有匹配的数目, 记为μ(G). 该指标与物质的沸点、熵、化学键的计算和化学结构等有着密切的联系, 且有着较为广泛的应用, 相关的应用参见文献[2-4]. 文献[5]中确定了单圈图关于Hosoya指标的排序; 文献[6]中确定了双圈图中最小的Hosoya指标, 并刻画了相应的极图; 文献[7]中确定了一类特殊双圈图的Hosoya指标的排序; 文献[8]中确定了连通的三圈图中最小的Hosoya指标, 并刻画了相应的极图; 文献[9]中研究了这类三圈图关于Merrifield-Simmons指标的排序. 本文主要研究了文献[9]中所给的三圈图Tk关于Hosoya指标的排序问题.

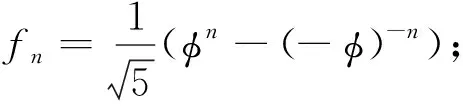
图1 三圈图Tk、Tk+1和Tk+2

图Tk是由三个圈Cm、Cq和Cn构成的三圈连接图, 其中Cm和Cq共用一条边ab,Cq和Cn共用一条边vkvk+1. 类似的可以定义Tk+1和Tk+2, 如图1所示.

1 预备知识

在证明主要结论之前, 我们先介绍以下几个引理:

引理1[3]设G是一个简单的连通图, 对任意的v∈V(G),uv∈E(G), 则

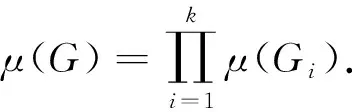
引理3[3]对于n阶的路Pn, 有μ(Pn)=fn+1.

引理4[3]对于n阶的圈Cn,有μ(Cn)=fn+1+fn-1.

由引理1～4我们可得以下结论:

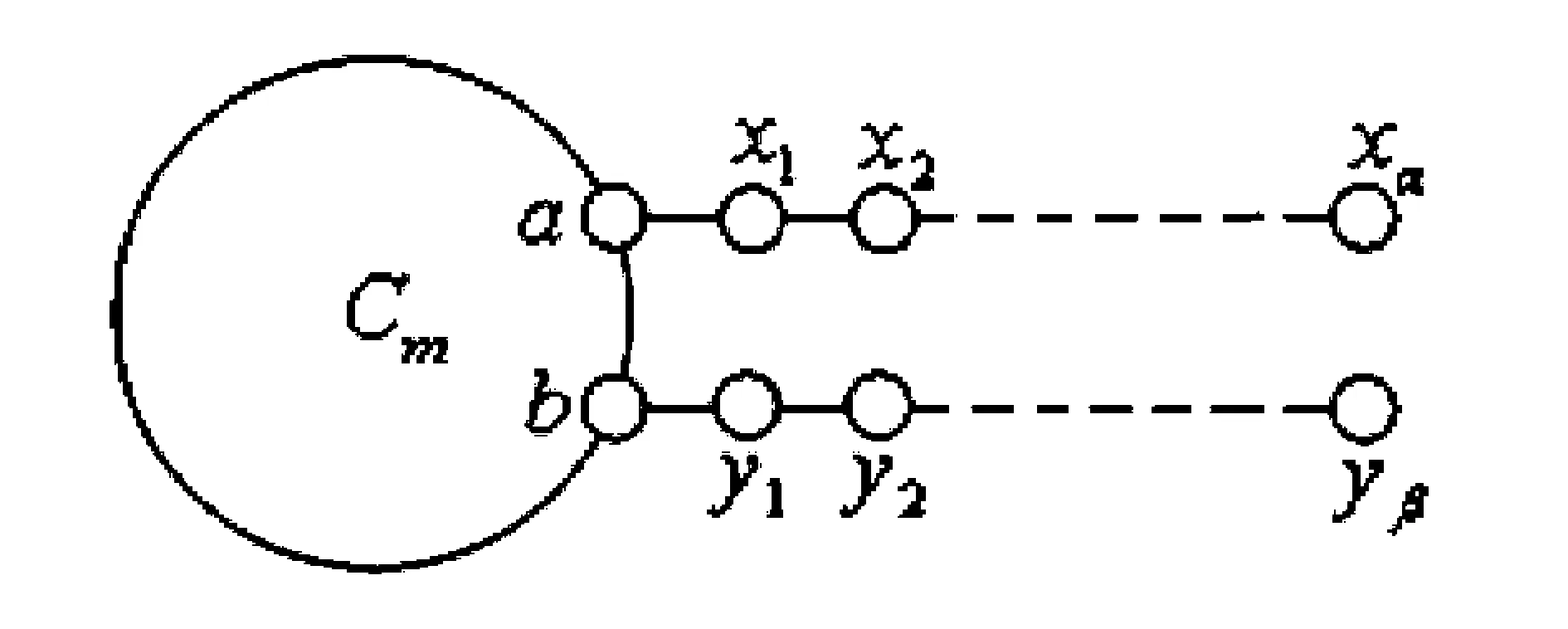
图2 图H

引理6 对于如图2所示的图H, 有

μ(H)=(fm+1+fm-1)fα+1fβ+1+fm(fα+1fβ+fαfβ+1)+fm-1fαfβ.

证明由引理可知

μ(H)=μ(H-ax1)+μ(H-a-x1)

=μ(H-ax1-by1)+μ(H-ax1-b-y1)+μ(H-a-x1-by1)+μ(H-a-x1-b-y1)

=(fm+1+fm-1)fα+1fβ+1+fmfα+1fβ+fmfαfβ+1+fm-1fαfβ

=(fm+1+fm-1)fα+1fβ+1+fm(fα+1fβ+fαfβ+1)+fm-1fαfβ.

2 主要结果及其证明

该类三圈连接图Tk关于Hosoya指标的排序, 我们可以得出以下结论:

证明如图1所示, 由引理可知

μ(Tk)=μ(Tk-υκυκ+1)+μ(Tk-υκ-υκ+1)

=μ(Tk-vkvk+1-ab)+μ(Tk-vkvk+1-a-b)+μ(Tk-vk-vk+1)

=(fm+n+q-3+fm+n+q-5)+fm-1fn+q-3+

fn-1·[(fm+1+fm-1)fkfq-k-2+fm(fkfq-k-3+fk-1fq-k-2)+fm-1fk-1fq-k-3].

同理, 可得

μ(Tk+1)=(fm+n+q-3+fm+n+q-5)+fm-1fn+q-3+

fn-1·[(fm+1+fm-1)fk+1fq-k-3+fm(fk+1fq-k-4+fkfq-k-3)+fm-1fkfq-k-4]；

μ(Tk+2)=(fm+n+q-3+fm+n+q-5)+fm-1fn+q-3+

fn-1·[(fm+1+fm-1)fk+2fq-k-4+fm(fk+2fq-k-5+fk+1fq-k-4)+fm-1fk+1fq-k-5].

下面比较μ(Tk)与μ(Tk+1)的大小关系.

μ(Tk)-μ(Tk+1)=fn-1·[(fm+1+fm-1)(fkfq-k-2-fk+1fq-k-3)+

fm(fk-1fq-k-2-fk+1fq-k-4)+fm-1(fk-1fq-k-3-fkfq-k-4)].

由引理5可知

因此, 有

μ(Tk)-μ(Tk+1)=(-1)kfq-2k-3fn-1·[-(fm+1+fm-1)+fm+fm-1]=

(-1)k+1fq-2k-3fm-1fn-1.

故当k为偶数时，μ(Tk)<μ(Tk+1)；当k为奇数时,μ(Tk>μ(Tk+1).

下面比较μ(Tk)与μ(Tk+2)的大小关系.

μ(Tk)-μ(Tk+2)=fn-1·[(fm+1+fm-1)(fkfq-k-2-fk+2fq-k-4)+

fm(fkfq-k-3+fk-1fq-k-2-fk+2fq-k-5-fk+1fq-k-4)+fm-1(fk-1fq-k-3-fk+1fq-k-5)].

由引理5可知

因此, 有

μ(Tk)-μ(Tk+2)=(-1)kfq-2k-4fn-1·[-(fm+1+fm-1)+fm+fm-1]=(-1)k+1fq-2k-4fm-1fn-1.

故当k为偶数时,μ(Tk)<μ(Tk+2)；当k为奇数时,μ(Tk)>μ(Tk+2).