电动汽车无线充电系统的功率控制方法

2018-10-30宋亮张希李哲

传动技术 2018年3期

宋亮张希李哲

(上海交通大学，上海 200240)

0 引言

在世界范围内化石能源向清洁能源转换的大环境下，传统汽车行业的压力日益增大。随着奔驰、大众等车企相继公布了取消燃油车的时间日程表，市场迫切需要一种可以取代传统燃油车的新能源汽车的出现。在众多的新能源汽车中，电动汽车的发展最好且应用最为广泛，传统汽车的电动化势在必行。目前，电动汽车普及的最大障碍是充电问题。与通用的有线充电方式相比，电动汽车的无线充电有着方便快捷、安全稳定的特点，并且可以省去充电桩占用的空间，因此比有线充电有更广阔的应用前景[1]。

电动汽车无线充电基本的拓扑类型有SS,SP,PS,PP四种类型[2]，基于这四种基本拓扑又演变出混合拓扑类型，如S-SP[3],LCL[4]等。在众多无线充电拓扑中，集成LCC补偿拓扑由于其谐振频率不随耦合系数及负载情况的变化而变化[5-6]，同时输出端电流与负载无关可视作恒流源的特性被广泛研究[7]。然而，对于此种拓扑的功率控制问题相关研究较少。本文对使用集成LCC补偿拓扑的无线充电系统进行研究，利用此种拓扑输出为恒流源的特性增加BUCK电路来对系统传输功率进行控制，通过控制器调节BUCK电路中MOSFET的占空比实现功率的精确控制。根据实际充电情况，提出了恒电流模式与恒功率模式两种控制模式。

图1 无线充电系统整体结构Fig.1 The structure of the wireless charging system

1 无线充电系统介绍

本文所研究的无线充电系统结构如图 1。系统的输入为直流稳压源，输出为车载电池。整个系统可以分为前端的集成LCC补偿拓扑与后端的BUCK电路两部分。S1～S4组成逆变器，将直流信号转为高频交流信号，此信号通过集成LCC补偿拓扑将能量由初级侧传输到次级侧，再经过D1～D4的整流与C3的稳压作用将感应出的交流信号转换为直流信号。然后通过BUCK电路将能量传输给电池，在这里通过调节BUCK电路的占空比可实现系统传输功率的调节。下面将对集成LCC补偿拓扑与BUCK电路进行详细分析。

1.1 集成LCC补偿拓扑及其开路效应

集成LCC补偿拓扑是在传统的LCC补偿拓扑基础上，将主线圈L1,L2与副线圈Lf1,Lf2叠放在一起进行耦合，节省了空间。对其进行分析首先要将三对耦合的线圈进行解耦，将系统中的互感线圈进行T型解耦并进行受控源等效后，集成LCC补偿拓扑可以简化为图 2。为了分析方便，将逆变器产生的高频方波由其一次谐波近似替代，忽略高次谐波的影响。同时，认为拓扑中所有器件均为理想型器件。

如果对器件参数进行～式进行等效，可进一步将拓扑简化为图 3。

Lpf1=Lf1+M1

(1)

Lpf2=Lf2+M2

(2)

Lp1=L1+M1-1/(ω2C1)

(3)

Lp2=L2+M2-1/(ω2C2)

(4)

Cpf1=Cf1/(ω2M1·Cf1+1)

(5)

Cpf2=Cf2/(ω2M2·Cf2+1)

(6)

这里p代表初级侧，s代表次级侧。从图 3中可以看出，如果经过上述等效原则，该拓扑可以视作LCL拓扑，而LCL拓扑的一个重要特点就是其输出可以视作恒流源[8]。

在初级侧，如果假设

Lpf1=Lp1

(7)

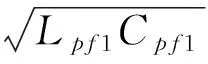
(8)

可得

(9)

(10)

图2 集成LCC系统进行解耦和受控源等效后结构图Fig.2 The equivalent decoupled structure

图3 选取特定参数后的结构化简图Fig.3 The simplified structure

jωLpf1

(11)

(12)

同理，在次级侧，如果假设

Lsf2=Ls2

(13)

ω0=1/Lsf2Csf2

(14)

可得到

jωLsf2

(15)

(16)

可得

(17)

(18)

·kU1U2

(19)

在一般的应用中，输入电压U1为固定值，那么系统的传输功率仅与U2有关。由此，可以通过控制U2的大小来控制系统传输功率的大小。

在极端情况下，如果系统开路，由于输出电流ILf2仅受输入电压U1的影响，电容C3上的电荷累加将导致U2急速上升，最终超过可承受的最大电压而损坏。因此，想要系统稳定运行，集成LCC补偿网络不可以开路。可以采用释放C3上电荷的方法控制C3两端的电压，考虑到当U1一定时传输功率P同U2存在如式关系，因而可以通过控制C3释放电荷的速率来控制系统的传输功率。

由以上讨论可以想到，在集成LCC补偿网络末端与车载电池之间可以加入BUCK电路控制U2的大小。与传统BUCK电路不同的是，由于车载电池的钳位效应的影响，此BUCK电路的控制量为输入电压Ubin。一般的车载电池要求充电电流平稳，因此加入的BUCK电路应该工作在连续模式。对于工作在连续模式下的BUCK电路，稳态工况下其输入输出电压同占空比存在如下关系

(20)

在这里，Uo为车载电池电压，即Ubat, 此电压在充电过程中会逐渐升高，并在当电池SOC接近饱和式趋于稳定。然而，车载电池电压的变化速率同BUCK电路的控制速率相比十分缓慢，因此，在上式中可以认为车载电池电压恒定。Ubin为BUCK电路的输入电压，在理想条件下，Ubin与U2相等，关系如，由于U2同系统传输功率P存在线性关系，可通过控制Ubin控制传输功率。

Ubin=U2

(21)

与传统的BUCK变换器不同，在这个应用中BUCK变换器的输出电压为固定值而输入电压不定。造成这样的不同在于：(1) 此BUCK电路的负载为电池，电池的钳位效应造成输出电压恒定；(2) 此BUCK电路的输入为一电流源而不是电压源，根据前文的推导可得，BUCK电路的输入电流可表达为式经过整流滤波之后的电流，可以表示为

(22)

此电流仅受电路参数和初级侧电压U1的影响，因此可以视作恒流源。在此恒流源的影响下，电荷会逐渐在C3处累积造成U2电压上升，此时可以通过调节S5的占空比使电荷以一定速率释放从而使U2稳定在一定的值附近，进而控制系统的传输功率。

1.2 无线充电系统功率控制方法

根据前文分析，可以以BUCK电路输入端的电压作为反馈来控制系统的传输功率，控制逻辑如图 4。

图4 BUCK电路控制逻辑图Fig.4 The control diagram of the proposed BUCK circuit

令状态变量x如式

(23)

即

(24)

由前文所述，此BUCK电路的输入可近似为恒流源，则有

(25)

当S5闭合时，有

(26)

(27)

于是可以得到状态方程

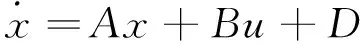
(28)

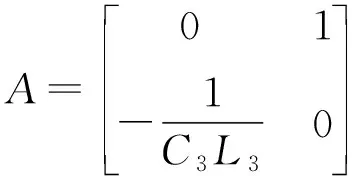
(29)

其中γ>0 。

(30)

实际的充电过程中，有恒电流充电和恒功率充电两种模式。在恒电流充电中，要求电池充电电流恒定Ic，充电功率随着电池SOC的升高而增大，此时可取

(31)

在恒功率充电中，要求系统充电功率不随电池电压的变化而变化，始终保持在预设值Pc附近，此时可取

(32)

2 实验

根据前文分析，搭建了一个基于集成LCC补偿拓扑的无线充电系统，如图 5所示，实验中用电子负载代替车载电池。实验中逆变器S1上的波形与ILf1的波形如图 6所示。在实际的充电过程中，有恒功率和恒电流两种工况。在电池SOC较低的工况下，希望充电电流恒定，此时应当是充电功率随着电池电压增加而增加；在电池SOC达到某一值之后，更好的充电方式是恒功率充电，此时希望系统传输功率恒定。据此，在保持输入电压400 V恒定，电池电压随着电池SOC的上升从98 V上升到129 V的情况下，对系统的充电功率进行控制，充电曲线如图 7所示。

图6 实验中Lf1与MOSFET S1上的波形图Fig.6 The Waveform of Ilf1 and voltage on S1

图7 电池电压、传输功率充电曲线Fig.7 Battery voltage and power transferred curves

可以看出，在电池电压从98 V～116 V之间，系统处于恒流状态，电流保持稳定，充电功率与电池电压曲线保持一致，二者的比值恒定,充电功率逐渐上升。在电池电压达到116 V以后，由于电池本身的充电特性，电池电压快速上升，但是在此时切换系统控制逻辑，将充电模式变为恒功率模式，充电功率曲线不随电池电压的迅速升高而变化，传输功率保持在2.89 kW附近。