基于OWA算子的三角模糊数多属性组合决策方法

林友谅，李 武，秦小丽

（1.湖南理工学院a.经济与管理学院；b.信息科学与工程学院，湖南 岳阳 414006；2.宿迁学院 商学院，江苏 宿迁 223800）

0 引言

对于给出信息为三角模糊数的多属性决策问题，学者们依据不同的假设提出了很多研究方法[1-6]。受运作机理差异影响，不同决策方法可能导致差异性的结果。由于决策过程外部条件和自身知识水平制约，决策者通常难于选择恰当的决策方法，因此，为提高决策的准确性，利用文献[7]提出的“组合”思想进行决策非常重要。“组合”研究可分为基于评价值[8,9]和基于评价序[10]的研究，一般认为，评价值较序值有更大的信息量，因而较多学者利用评价值进行“组合”研究，而运用评价序进行“组合”研究的文献相对较少。对于三角模糊数决策问题，因为去模糊化方法或者决策原理的差异，各种方法得出的评价值会有较大差异甚至不具有可比性，从而更需要研究基于评价序的组合评价方法。现有关于序数组合决策的研究方法主要有序号总和法、均值法、borda法、copeland法等，尚未见文献利用有序加权平均(OWA)算子[11]研究组合评价或组合决策问题。而OWA算子关注决策过程中集结位置的重要性[1,2,12,13]，可集结各类决策信息，已被广泛应用于决策分析、模糊系统等领域，在信息集成方面有其特有优势,应该可以利用OWA算子来研究组合决策问题。OWA算子应用的关键问题在于如何确定位置的权重，对于组合研究问题，适宜采用“基于离散正态分布思想”[13]的赋权方法，而新的赋权公式的提出也很有意义。

基于此，本文提出两种新的赋权公式，并基于OWA算子研究组合决策方法,利用多种决策方法对多属性决策问题进行初次求解,然后对决策序值利用OWA算子进行集结，进而确定方案最终排序，为解决属性值为三角模糊数的多属性决策问题提供一种新的思路。

1 问题描述

对于一个三角模糊数多属性决策问题,设有m个方案，A={A1,A2,…,Am}，n个决策属性，C={C1,C2,…,Cn}，属性权重ω={ω1,ω2,…,ωn}，满足ωj∈ [0,1]，且记第i个方案Ai对第j个属性Cj的属性值为âij(i=1,2,…,m;j=1,2,…,n)，[m×n为属性矩阵，其中âij为三角模糊数。决策者有l种可选的决策方法,L={L1,L2,…,Ll}，需要求出所有备选方案的最终排序结果。

2 基于OWA算子的序数组合决策方法

2.1 决策阶段

如表1所示，以上问题的解决可分三个阶段，去模糊化，多属性决策，结果组合。

表1 三角模糊数多属性组合决策过程

几何距离法也是常用的方法，有：

梯级平均综合表示法去模糊化后的值：

多属性决策：该阶段利用属性权重与属性评价值集结出各方案的综合值。主要有加权和法（SAW），加权积法（WP）和TOPSIS法等多种决策方法。对于效益性指标,设属性权重为ω={ω1,ω2,…,ωn}，属性评价值为rij,则多属性方法计算如下。

加权和法计算方法如式（4）,其原理是先将属性权重与属性评价值分别相乘,再求和汇总得出综合值Vi,Vi越大,方案 Ai越优。

加权积法计算方法如式（5）所示，其原理是先对属性值按属性权重求幂,再求积得出综合值Vi，Vi越大，方案Ai越优。

TOPSIS法先按式（6）分别确定正、负理想解,再按式（7）求出方案 Ai与理想解的距离和ˉ,再按式（8）计算出综合值Vi。Vi越大,方案Ai越优。

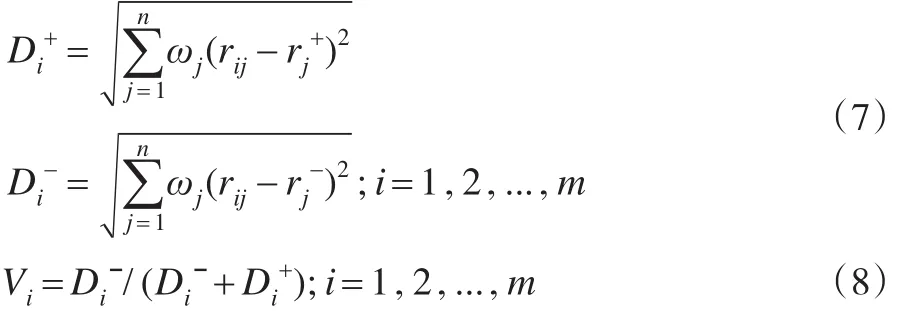
组合决策阶段：前面两个阶段选择的方法不同，可能产生不同的排序结果，该阶段将各种方法的排序结果进行组合，基于OWA算子，确定方案最终排序。

2.2 OWA算子

定义1[1-3]：设f:Rn→R 为n元函数,若 f(a1，a2，...，an)=，其中bj是a1,a2,…,an中按从大到小的顺序排列的第j个大的数，W=(w1,w2,…,wn)T是与f关联的加权向，则称函数f是n维有序加权平均算子，简记为OWA算子。

OWA算子的特点在于需对数据ai从大到小排序再进行加权集结，权重wj只与元素ai所在的位置存在联系。当W=(1,0,…,0)T时，OWA算子简化为max算子；W=(0,0,…,1)T时，OWA算子简化为min算子；当W=(1/n,1/n,…,1/n)T时，OWA算子简化为简单算术平均算子。当W=(0,1/(n-2),1/(n-2),…,1/(n-2),1/(n-2),0)T时，OWA算子简化为剔除极值的算术平均算子。赋权规则的多样化使得OWA算子具有广泛性，文献[13]对已有的OWA算子的赋权方法进行综述，并从正态分布特征出发提出“基于离散正态分布思想”的新的赋权方法。

受文献[13]的启发，本文给出两种新颖的赋权的方法，分别如式（9）和式（10）：

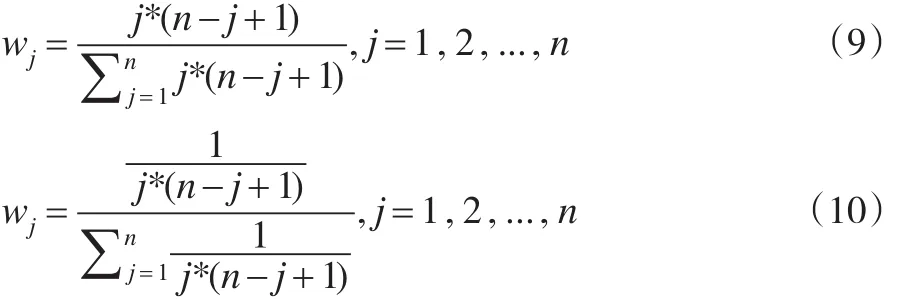
易证明基于式（9）和式（10）赋权的OWA算子具有对称性且服从离散正态分布，基于式（9）赋权的OWA算子的权重先递增，然后递减，而基于式（10）赋权的OWA算子的权重先递减，然后递增。证明略。

决策过程可能存在某些特有决策方法使得其排序结果不同于其他方法。由于这些特有方法的差异性，组合决策过程若决策者有尽量减弱特有方法影响的偏好，可以选择基于式（9）赋权的OWA算子对各方法的排序结果进行组合。若决策者有尽量加强特有方法影响的偏好，即更希望了解特有方法所造成的影响，可以选择基于式（10）赋权的OWA算子。

2.3 决策方法步骤

由于不同方法可能得出差异结果，在决策具体应用中，决策者应对多种方法的结果进行组合，以三种去模糊化方法和三种多属性方法进行组合决策为例，决策方法步骤如下：

第一步：获得属性的权重ω，以及各属性下的评价值矩阵Rj。

第二步：先将属性权重和评价值分别采用面心法、几何距离法、梯级平均综合表示法去模糊化处理，然后利用属性权重和评价值分别采用加权和法、加权积法、TOPSIS法集结出各方案的综合评价值。

第三步：将各方法的综合评价值转化为序数。

第四步：对各方法的评价序采用OWA算子进行集结。先对每个备选方案的序数进行大小比较，再根据决策者的偏好选择本文提出的基于式（9）赋权的OWA算子或基于式（10）赋权的OWA算子进行信息集结，最后对集结值进行排序，确定方案的最终排序。

3 实例分析

为更好的阐述本文方法及验证有效性，采用文献[5]的算例进行计算，比较和分析，按文献[7]方法的规范化结果见下页表2。假设属性重要性权重为w=(0.169,0.165,0.164,0.167,0.164,0.171)T。

步骤1：获得如上属性权重和表2的评价值。

步骤2：采用不同的决策方法确定各方案的综合评价值，表3（见下页）第一行为去模糊化方法，第二行为多属性决策方法，采用COA+SAW计算出方案的评价值分别为2.018，2.036，1.991，1.970，1.999。

表2 规范化决策矩阵×(10-1)

步骤3：将表3各方法的综合评价值转化为序数。表3中方法依序与表4的方法对应，表3的COA+SAW对应表4中的法1。

表3 各方法下的方案综合评价值

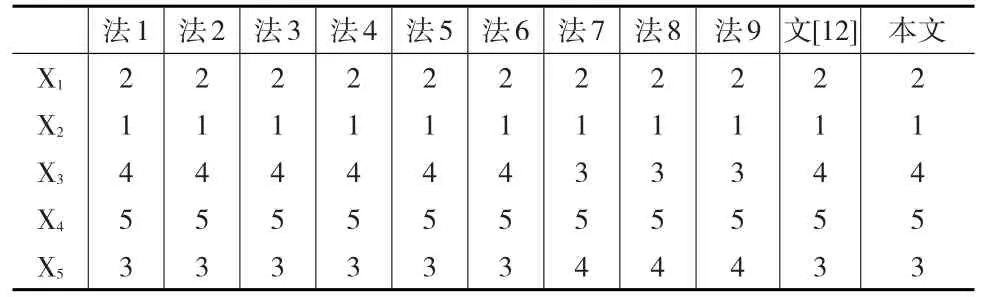
表4 各方法下的序数

步骤4：n=9,利用式（9）可以计算出权重系数为(0.055,0.097,0.127,0.145,0.152,0.145.0.127,0.097,0.055),用OWA算子求出方案综合值(2,1,3.72,5,3.28),方案排序 X2＞X1＞ X5＞X3＞X4。利用式（10）可以计算出权重系数为(0.196,0.110,0.084,0.073,0.070,0.073,0.084,0.110,0.196),用OWA算子求出方案综合值(2,1,3.61,5,3.39),方案排序仍为 X2＞X1＞ X5＞X3＞ X4。

如表4所示，本文采用基于式（9）和式（10）赋权OWA算子的组合结果与文[12]的均值法的结果相同,说明本文方法有效。但是，若考虑属性权重的不确定，可选择的方法可能更多，对于文[12]指出的序数为{1,3,3,6}和{1,2,5,5}或其他类似的数，它们均值相等，方差相等，按以前的均值法无法区分出方案的差异，而采用基于式（9）的OWA算子，则可以计算出应赋权(0.2,0.3,0.3,0.2)，OWA式(9){1,3,3,6}=3.2,OWA式(9){1,2,5,5}=3.3；若采用基于式（10）的OWA算子，OWA式(10){1,3,3,6}=3.3,OWA式(10){1,2,5,5}=3.2。根据决策者的偏好采用本文方法即可区分方案的优劣，这也说明本文方法的可行性和有效性。

4 结论

本文对属性值以三角模糊数形式给出的多属性决策问题进行研究，考虑三角模糊数去模糊化和多属性决策都有多种方法，而决策者又无法选择合适方法的情况，提出一种基于OWA算子的组合决策方法。本文提出的方法一方面综合多种决策方法的意见，可以较好地避免决策方法选择有误的问题；另一方面按离散正态分布思想提出OWA算子的两种新的赋权方法,决策者根据自己的偏好选择合适的赋权方法,再对各方法排序结果进行组合,既符合实际，又丰富了OWA算子。当然，该方法算法简单，也只从是增强还是减弱特有方法影响的角度对决策问题进行分析，对于组合决策问题及决策者的偏好特征的差异，仍值得深入探讨。