时变环境下RCS测量中的精确背景抵消处理技术

2018-10-30原赛赛梁丽雅许小剑

北京航空航天大学学报 2018年10期

原赛赛，梁丽雅，许小剑

(北京航空航天大学电子信息工程学院, 北京 100083)

低可探测目标的雷达散射截面(RCS)精确测量与评估对RCS测试场的低散射背景电平提出了越来越高的要求。为了减小RCS测量不确定度，提高测量精度，通常采用背景矢量相减技术以抑制背景杂波的影响[1-5]。然而，对于室外RCS测试场，尤其是地面平面场，在测量背景和目标这段较长时间内，由于外部环境因素的影响，雷达系统和测试场特性均可能随时间发生漂移，具体表现为温度、湿度等影响雷达系统稳定性、测试场地面反射系数以及传播路径电长度等受光照、温度影响随时间变化。雷达系统-测试场的时变特性导致已测得的背景数据同当前的目标测量数据非完全相干，直接背景矢量相减效果不理想甚至完全失效。

LaHaie等提出通过补偿背景测量随频率和不随频率变化的相位来消除时变因素给背景抵消带来的不利影响[6]。事实上，如果可以估计出雷达系统-测试场随时间的变化，即由于环境变化带来的测量系统-测试场传递函数幅度起伏和相位变化，则可以对目标回波和背景回波做幅度、相位补偿，把所测数据校准到完全相干，从而实现精确的背景抵消处理[7]。

本文针对RCS测试外场受时变因素影响大的问题，建立了测量系统-测试场的时变传递函数参数化模型，并提出利用软件距离门技术提取辅助校准区域数据来估计模型参数，实现对时变响应特性的精确幅度和相位补偿。经幅度、相位补偿后的数据用于背景相减处理可以实现精确的背景抵消。实验结果验证了本文技术和算法的有效性。

1 RCS测量中的时变传递函数模型

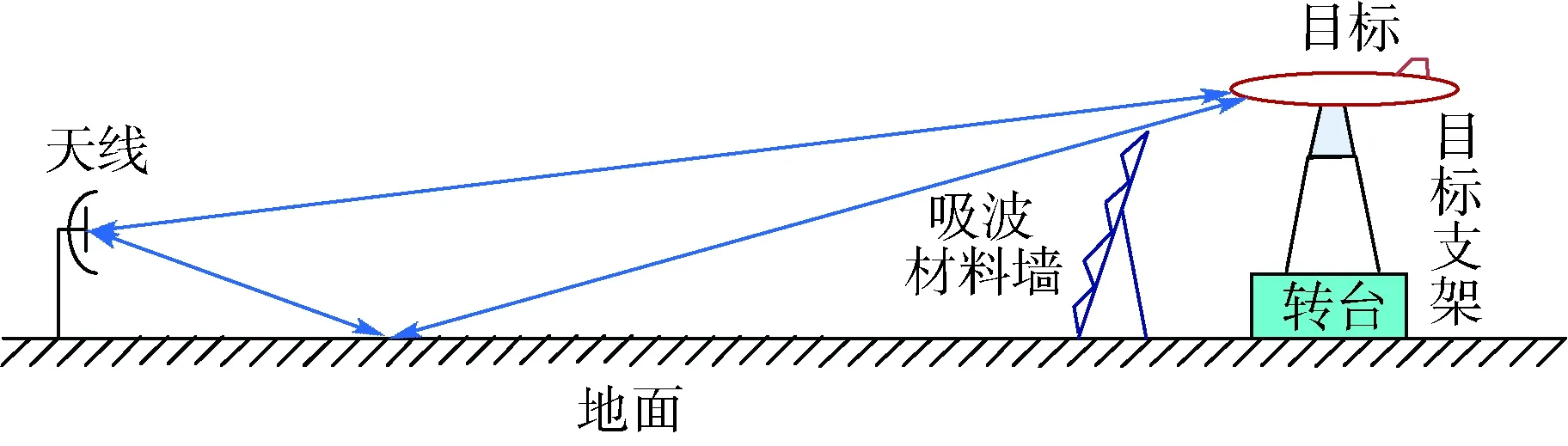
图1 RCS测量几何关系示意图Fig.1 Schematic diagram of geometry for RCS measurement

采用地面平面场的室外RCS测试场典型测量几何关系如图1所示。由于发射波和散射回波的传输路径均包括直接散射、地面一次和二次反射共3条路径，而经由一次和二次反射路径的回波信号均受地面反射的影响，具体表现为测试场地面反射系数以及传播路径电长度均随测量时间而变化。在室外测试场，测量系统受温度、湿度影响，系统特性也可能随时间发生漂移。为了提高此类RCS测试场背景抵消处理的有效性，应该考虑测试场、测量系统时变特性的影响[5]。

若引入测量系统-测试场的时变传递函数来表征测量系统-测试场变化对雷达接收回波的影响，测目标和测背景时的雷达回波信号可分别表示为

S(f,t)=H(f,t)(T(f)+B(f,t))

(1)

SB(f,t)=H(f,t)B(f,t)

(2)

式中：H(f,t)为测量系统-测试场的传递函数，是随时间慢变化的，反映了测量雷达系统漂移和测试场类型及其电参数随时间变化的特性，f为频率，t为时间；S(f,t)和SB(f,t)分别为测目标和测背景时雷达接收到的回波信号，两者都是随时间变化的；T(f)为目标在给定姿态下的真实散射场，不随时间变化；B(f,t)为固有背景散射，随时间变化[7]。

假设在t1时刻测背景，t2时刻测目标，这样，背景抵消在数学上可表示为[8-9]

S(f,t2)-SB(f,t1)=

H(f,t2)(T(f)+Δ(f,Δt12))

(3)

(4)

式中:Δ(f,Δt12)为经背景抵消后的剩余背景误差，Δt12为t1和t2的时间差。仅当B(f,t2)=B(f,t1)，H(f,t2)=H(f,t1)时，有

Δ(f,Δt12)=0

(5)

可见，如果测试场背景是随时间变化的，经过多次测量和信号处理并不能解决背景抵消中剩余背景误差的问题。但是对于一个经过仔细设计和优化的测试场，在测试过程中其目标区一般不会发生变化，即

B(f,t2)=B(f,t1)=B(f)

(6)

则式(4)变为

(7)

若要求剩余背景误差为0，则要求

H(f,t2)=H(f,t1)

(8)

即在测目标和测背景时刻测量系统-测试场的时变传递函数相同。

在外场长时间RCS测量中，式(8)一般不可能满足，可以通过对当前数据进行幅度和相位补偿使之满足，从而实现精确的背景相减。

若将传递函数表示为参数化的形式

(9)

式中：A(t)为随时间变化的幅度增益；c为光速；α(t)和β(t)分别为随频率线性变化的相位因子和不随频率变化的固定相位因子，两者均随时间慢变化。这样，对于t1、t2时刻，有

(10)

可见，只需估计出3个参数A12、α12、β12，便可完成传递函数的幅、相校准，从而将提前测得的背景信号(t1时刻)等效到当前测目标时的背景信号(t2时刻)。在此基础上进行背景抵消处理，得到

H(f,t2)(T(f)+B(f))-

(11)

从而实现时变环境下的精确背景抵消。

2 传递函数的参数估计技术

2.1 背景抵消流程

在第1节讨论中，笔者只考虑了测背景和测目标之间系统传递函数的变化。在实际外场测量中，若对目标做360°全方位测量，测目标和测背景都需要较长时间，测量系统-测试场随时间的变化导致不同时刻测得的回波数据非完全相干，进而影响背景抵消效果。为了得到完全相干的目标数据和背景数据，可以选定一个测量时刻为参考时刻，将所有其他时刻测得的数据校准到这个时刻，然后进行背景相减处理。RCS测量通常为扫频扫角测量，即随时间变化，转台旋转不同方位角。可以将任意一个方位角下数据作为参考数据，其他数据与之做校准。具体流程如图2所示。

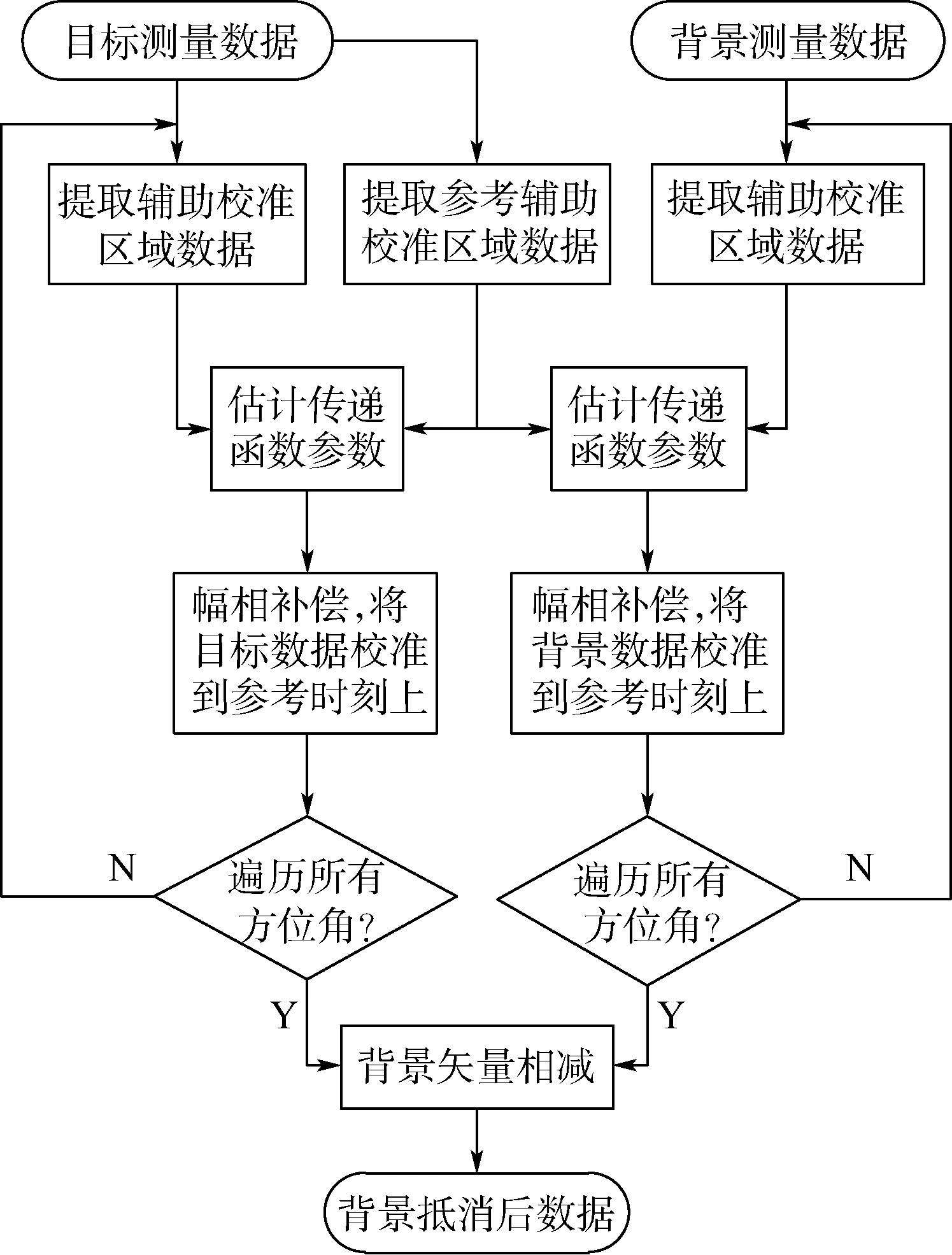
图2 校准与背景抵消处理流程Fig.2 Procedure for correction and background subtraction processing

2.2 辅助校准区域选取

对传递函数进行校准，需要估计3个参数，精确的参数估计算法要求用于参数估计的2部分数据y1(f)和y2(f)只有幅度和相位的差别[10-11]，即满足

(12)

式中：A、α和β为待估计的参数。显然，雷达测得的背景数据和目标数据不满足此要求，不能直接用于参数估计。

为了引出该问题的解决方法，笔者课题组首先给出一组实测数据某一方位角下的高分辨率一维距离像[12]，如图3所示。图中所用数据为微波暗室对椭球体的测量数据，测量几何关系与图1类似，在距离目标支架约0.65 m处设置了一堵吸波材料墙，用于减少目标支架等对雷达回波的影响。先测得背景数据，再对目标做360°方位旋转测量。测量频段4～8 GHz，频率步长5 MHz。

图3 高分辨率一维距离像Fig.3 High-resolution 1D range profile

由图3可以看出，目标信号与背景信号一维距离像的差别主要在椭球所在区域，其他背景区域相对重合较好。尤其在吸波材料墙区域，几乎完全重合。

若通过如图3中的软件距离门，分别将吸波材料墙从目标和背景的一维距离像中提取出来，然后再做快速傅里叶变换(FFT)，即得到吸波材料墙在测背景和测目标时的数据。这2组数据只有因测量系统-测试场时变传递函数变化带来的幅度和相位的差别，满足式(12)，可以用来估计传递函数的参数[6]。

软件距离门是由一个带通滤波器来实现的，通过仔细设计，可以将指定区域的一维距离像准确地过滤出来。

对于没有设置吸波材料墙的测试场，只需采用类似的方法，分别从背景数据和目标数据中提取同一片区域(以下称为辅助校准区域)的数据，便可实现对传递函数参数的准确估计。辅助校准区域数据提取流程如图4所示。

辅助校准区域数据提取的精确性决定了参数估计的准确性。首先，辅助校准区域不应离目标区域太远，因为在室外测试场，不能保证整个测试场的变化特性完全一致。笔者更关心的是目标区的背景抵消效果，所以在目标区附近提取辅助校准区域，估计出的传递函数更能代表目标区测试场的变化。其次，在一维距离像上，辅助校准区域最好有明显的特征，这样能够用软件距离门准确提取出来，保证后续参数估计的准确性。最后，提取的辅助校准区域应该完全一致。由傅里叶变换的频移性质可知，随频率变化的线性相位会使一维距离像发生漂移，所以软件距离门中心位置不能简单地选取固定值。解决办法是将一定范围内一维距离像最大值处作为软件距离门的中心。

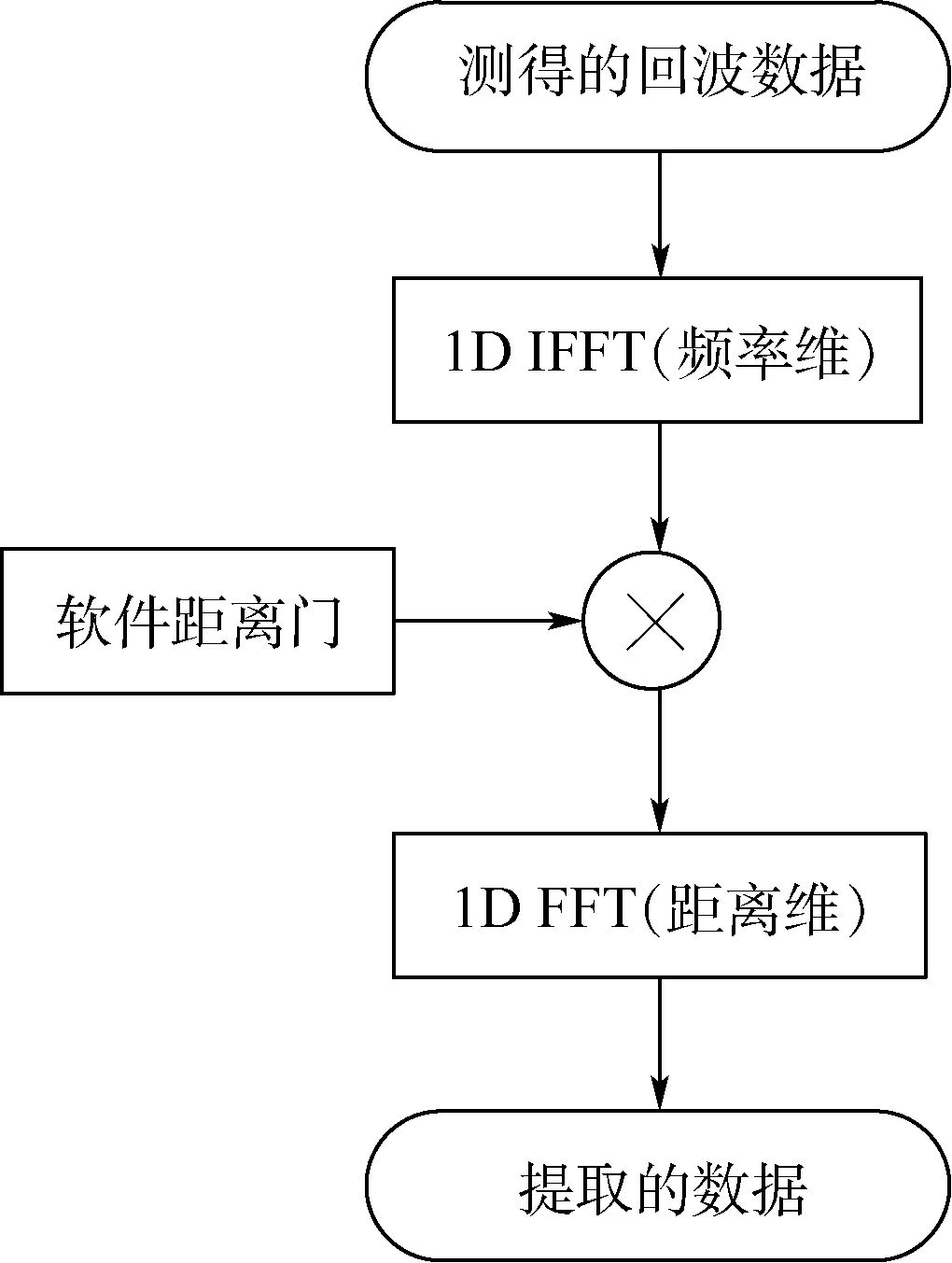
图4 辅助校准区域数据提取流程Fig.4 Procedure for data extraction in auxiliary calibration area

2.3 传递函数参数估计算法

假设提取出来的辅助校准区域在不同时刻的回波信号为yn1(f)和yn2(f)，满足

yn1(f)=y(f)+v1(f)

(13)

yn2(f) =H(f)y(f) +v2(f)

(14)

(15)

式中：v1(f)和v2(f)分别为不同时刻的噪声，高信噪比时可以忽略；H(f)为传递函数。一般情况下，雷达为扫频测量，即

f=f0+(k-1)Δfk=1,2，…,N

(16)

式中：f0为中心频率；Δf为频率步长。

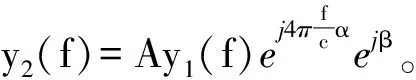
对抑制噪声后的信号补零至相同长度Nc，再做互相关处理。对y1(f)和y2(f)分别做Nc点的快速傅里叶逆变换(IFFT)得到Y1(n)和Y2(n)，则两者相关函数为

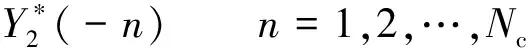
(17)

式中：⊗表示循环卷积。对式(17)两端做离散傅里叶变换，可得

(18)

式中：y1(k)和y2(k)分别为y1(f)和y2(f)的离散化后补零的值；*表示复共轭。因此有

n=1,2,…,Nc

(19)

将式(16)、式(17)代入式(20)，可得

(20)

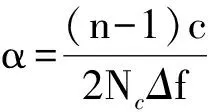
对A、β的估计，可以定义一个相干函数C，利用估计的线性相位补偿y2(k)，并用优化方法得到A、β的估计[14-15],有

(21)

3 实验结果与分析

3.1 微波暗室实测数据验证

为了验证时变环境下背景抵消技术的有效性，本文将该技术用于一组微波暗室实测数据。该数据与2.2节所用数据相同，选取遮挡墙区域作为辅助校准区域，如图3所示。

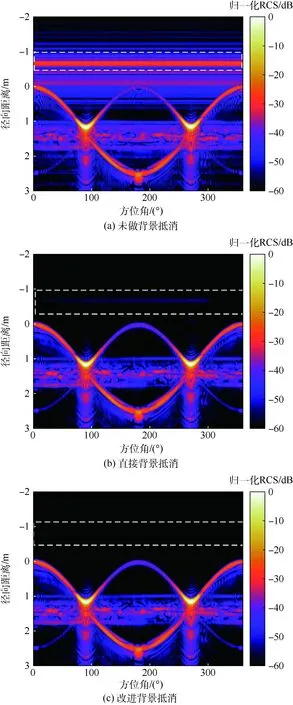
图5 室内实测目标数据高分辨率一维距离像对比Fig.5 Comparison of high-resolution 1D range profile of target using indoor measurement data

图5给出了目标高分辨率一维距离像随方位角的变化特性。其中图5(a)为未做背景抵消的目标一维距离像，图中不随方位角变化的横条为固定背景杂波，可以看出背景杂波很强。在径向距离-0.65 m处有一条明显的横条，为遮挡墙的一维距离像。图5(b)为用直接背景矢量相减算法抵消背景后得到的一维距离像。图5(c)为按图2所示流程做背景抵消处理后得到的一维距离像。对比发现，由于雷达系统-测试场的变化，直接背景矢量相减，-0.65 m处的墙的一维距离像仍然存在，背景信号并不能完全被抑制，而采用本文算法处理，遮挡墙的回波几乎被完全抑制，背景抵消效果更好。

同时，注意到经背景抵消处理后，在径向距离1～2 m处仍然存在剩余杂波，这是由于用于支撑目标的泡沫材料支架是随转台转动的，不同方位角下散射有所不同，而用于背景抵消的数据为单个方位角下的测量数据，故无法完全抵消这部分背景杂波。

3.2 外场测量仿真验证

(22)

(23)

(24)

图6给出了仿真数据的目标高分辨率一维距离像随方位角的变化特性。图6(a)为仿真目标数据的一维距离像。可以看出，由于存在线性相位的影响，一维距离像随时间(方位角)发生了漂移。图6(b)、(c)分别为用直接背景矢量相减算法和本文改进的背景抵消算法处理后得到的一维距离像。可以看出，直接背景矢量相减算法已经完全失效，使用本文算法处理，背景得到很好的抑制，从而验证了本文技术和算法的有效性。