矩孔夫琅禾费衍射的仿真模拟
2018-10-30吴云飞
吴云飞
矩孔夫琅禾费衍射的仿真模拟
吴云飞
(四川师范大学工学院,四川 成都 610000)
根据夫琅禾费衍射的数学模型,利用Matlab的高性能数值计算和可视化功能,编写m文件,仿真模拟了矩孔夫琅禾费衍射现象,仿真结果与实际理论吻合,同时仿真参数可以灵活设置,有助于举一反三,深入理解光学理论,辅助物理教学。
Matlab;仿真模拟;夫琅禾费衍射;光学理论
光的衍射是光波传播过程中遇到障碍物而偏离原来直线传播方向,进入障碍物的几何阴影区,并在屏幕上形成光强不均匀分布的现象[1]。衍射体现了光的波动性,而夫琅禾费衍射不仅反映出衍射的一些基本特性,又具有特殊的简单性。利用计算机仿真模拟这一衍射现象,不受实验场所和仪器限制,具有模拟结果逼真、改变实验参数灵活、观察实验现象直观的优点,有助于更好理解衍射现象。
1 矩形孔夫琅禾费衍射
利用透镜把衍射光会聚,可以在透镜的后焦面近距离观察夫琅禾费衍射现象。图1为采用透镜的夫琅禾费衍射光路图,图中给出了衍射屏0,0坐标平面和观察屏,坐标平面的坐标方向。
矩形孔中心位于平面光阑坐标原点,它沿着坐标0,0方向的半宽度分别为,.设光阑被单位振幅平面波垂直照射,光阑后方有一个焦距为的正透镜,平面波将变为向透镜焦点会聚的球面波。其中,紧贴孔径后方的物平面场分布为(0,0)=rect(0/2)×rect(/2),结合菲涅尔-基尔霍夫衍射公式和透镜的傅里叶变换性质知,令=,透镜后焦面即观测平面的衍射场为夫琅禾费衍射场[2]:

夫琅禾费衍射图像强度为:
2 仿真模拟结果
根据矩孔夫琅禾费衍射的数学模型,利用matlab的高性能数值计算和可视化功能,在Matlab中编写。m函数文件,保持入射波长和透镜焦距不变,设置入射光波长为632.8 nm,透镜焦距=100 mm,主要通过修改孔径尺寸,观察屏大小等仿真参数,得到观察屏上矩孔衍射图样的光强分布。

图1 夫琅禾费衍射光路示意图
2.1 方孔和矩孔仿真对比结果
设置矩孔尺寸(2,2),一组为(2 mm,2 mm),一组为(2 mm,4 mm),得到图2(a)和2(b)仿真结果。对比仿真结果,图2(a)和图2(b)在,方向上都出现明暗相间的条纹,其中图(a)的方孔衍射图样的条纹在,方向上明暗对称,完全相同;图(b)的矩孔衍射图像的条纹则在两个方向上明暗不同,在方向强度扩展更明显,条纹数目则明显少于方向,这是由于矩孔孔径长度之比2/2=1/2,方向的光束受到的限制大于方向,因此在方向上的衍射效应更明显。当进一步改变矩孔的宽度使得>,矩孔就成了狭缝,可以很容易地模拟单缝衍射的情况。
此外,以2=2 mm,2=2 mm情况为例,衍射屏上的相对光强沿轴的分布情况如图3所示,可以看出,中央明纹的宽度为其他所有明条纹宽度的2倍,衍射光强主要集中在中央明条纹区域,两边的一级明条纹的最大光强只有I0的4.7%,与文献[1]吻合。
2.2 方孔大小变化的仿真对比结果
保持孔径为方形,改变其大小依次为4 mm、10 mm、40 mm,观察衍射在观察屏的光强分布,得到的仿真结果如图4所示。
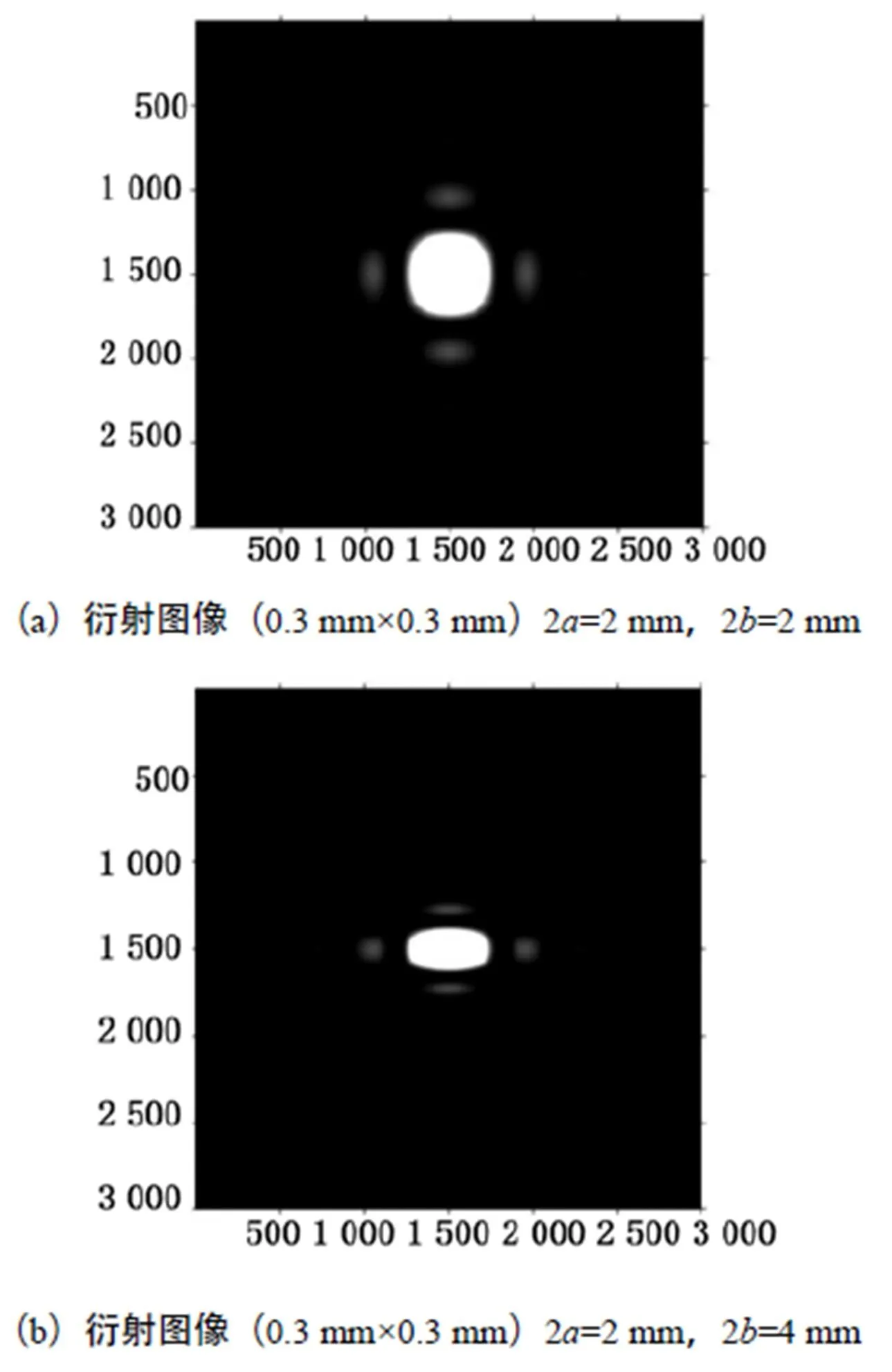
图2 衍射图像

图3 x轴上剖面的归一化光强曲线
从图4看出,随着孔径的增大,衍射效应不断减弱,条纹变窄,条纹数量增多。当孔径增大到40 mm时,衍射条纹几乎缩小为一个几何像点。这表明随着孔径的增大,光的衍射效应减弱,光的传播行为可以看成从衍射变为了直线传播,这与理论分析也相符。
3 结束语
本文利用Matlab软件仿真研究光学中的衍射问题,主要分析了矩孔大小变化对观察屏上光斑光强分布的影响,仿真结果与理论分析一致。此外,编程实现的衍射模拟程序简洁,响应速度快,修改程序参数可进一步模拟入射光波波长、光源的强度、观察的距离等因素对衍射结果的影响,体现出计算机模拟方法的灵活有效,借助这一研究手段将有助于深入理解光学衍射理论及进行辅助教学。
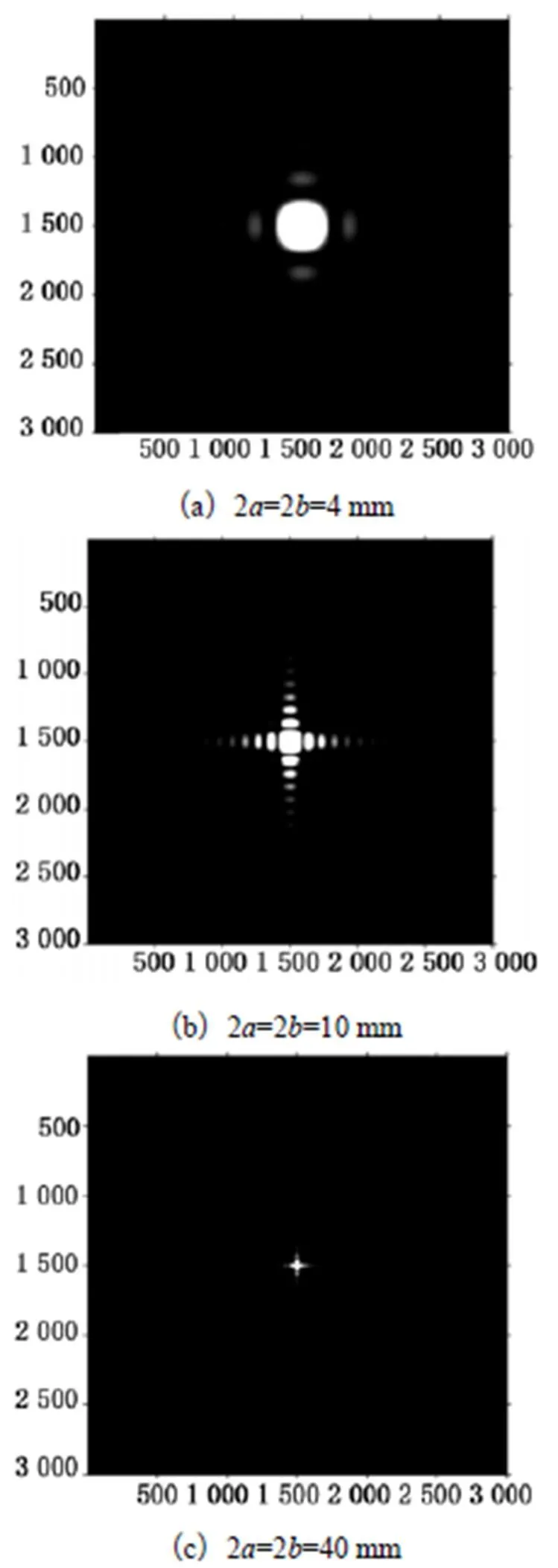
图4 方孔大小变化的二维衍射图
[1]梁铨廷.物理光学[M].北京:电子工业出版社,2016.
[2]李俊昌.衍射计算及数字全息[M].北京:科学出版社,2017.
[3]刘绒侠,杨郁.基于MATLAB的夫琅禾费矩孔衍射仿真[J].实验科学与技术,2013,11(4).
2095-6835(2018)20-0142-02
O436.1
A
10.15913/j.cnki.kjycx.2018.20.142
吴云飞(1980—),女,重庆人,硕士,讲师,研究方向为计算机应用技术、电气工程及其自动化。
〔编辑:严丽琴〕
