基于差分隐私的RDPk—means聚类方法
2018-10-29马哲鹿方凯
马哲 鹿方凯

摘要:为解决k-means聚类算法在聚类过程中隐私泄露风险,在满足ε-差分隐私保护前提下,提出一种隐私保护的RDPk-means聚类方法。该方法与传统随机选取初始点方式不同,采取基于网格密度的方式选取初始聚类中心,并在UCI数据集中进行有效性验证。采用543条数据生成2个聚类簇和19 020条数据生成3个聚类簇分别进行实验。结果表明,该聚类方法在不同的数据规模和维数情况下可以很好地保护数据隐私,能保证聚类结果的可用性。
关键词:k-means算法;差分隐私;隐私保护
DOIDOI:10.11907/rjdk.181386
中图分类号:TP309
文献标识码:A 文章编号:1672-7800(2018)008-0205-03
英文摘要Abstract:In order to solve the risk of privacy leakage in the clustering process of k-means clustering algorithm,under the premise of satisfying ε-difference privacy protection,this paper proposes a privacy-preserving RDPk-means clustering method.This method is different from the traditional random selection of initial points and it is based on the grid density approach to select the initial poly Class Center to verify validity in UCI's real data set.Two experiments were performed using 543 data sets to generate 2 clusters and 19,020 data sets to generate 3 clusters.The experimental results show that the proposed clustering method can still protect data privacy with different data sizes and dimensions,and also guarantee the availability of clustering results.
英文關键词Key Words:k-means algorithm; differential privacy; privacy protect
0 引言
大数据时代,随着数据量的急剧增长,全球范围内出现了对信息隐私的担忧[1]。由于互联网可以轻松地将数据自动收集并添加到数据库中,因此隐私问题进一步恶化。对大量数据收集的担忧已经延伸到应用于数据的分析工具。数据挖掘是当前对数据进行分析和处理的有效技术,可从大型数据库中发现有潜在价值的信息。但与此同时,敏感信息的泄露也给用户带来了不可估量的损失[2-4]。因此,对聚类分析中的隐私数据进行有效保护,成为数据隐私保护领域亟待解决的问题[5-6]。
针对上述问题已经有许多隐私保护方法,如文献[7-10]中描述的模型,但这些隐私保护模型需要不断改进以抵御新的攻击,如背景知识攻击[8]和合成攻击[9],其中一些并不能很好地解决数据可用性和隐私保护之间的平衡。因此,本文提出了一种在聚类分析中用于隐私数据保护的RDPk-means聚类算法。RDPk-means算法在k-means聚类算法的迭代过程中增加满足特定分布的适当随机噪声,使聚类结果在一定程度上失真,达到隐私保护目的,同时保证数据的可用性。
1 隐私保护研究现状
当前的隐私保护技术大致分为数据加密、限制发布和数据失真3类 [11]。数据加密是通过加密算法对数据加密,对数据进行有效保护;限制发布主要是在发布数据前对数据提前加密;数据失真是对数据添加噪声使数据失真,进而对数据隐私进行保护。
1.1 基于数据加密的隐私保护技术
1.1.1 对称加密算法技术
对称加密算法是最古老和使用最多的加密方法。在对称加密算法中,解密密文的密钥与加密明文密钥相同。这种加密算法现在被广泛使用,但是这种方法存在一定缺陷,即随着密钥数量的增加,用户对密钥的管理会变得很困难。
1.1.2 非对称加密算法技术
与对称加密算法不同,非对称加密算法使用两个密钥:一个密钥即私钥,只有一个人知道,另一个密钥即公钥,每个人都可以使用。这两个值在数学上相互关联,但从一个值得出另一个值是不可能的。该方法在数字签名和身份认证领域应用较广,但它的缺点是算法复杂,数据加密效率较低。
1.2 基于限制发布的隐私保护技术
1.2.1 K-匿名技术
K-匿名[12]是一种经典的匿名化方法,这种方法首先将所要发布的关系数据划分为多个等价类,每个等价类必须包含不少于K条相似数据,也就是说,在等价类中,任意一条数据都无法和其它K-1条数据区分[13],这使得满足k-匿名的数据具有较好的隐私保护能力。但是K匿名的缺陷也很明显,敏感属性是等价类中的重要因素[14],因为K-匿名并没有对此进行限制,所以当某个等价类的敏感属性取值相同时这种技术便会失效。
1.2.2 L-diversity技术
L-diversity[15]是基于K-匿名改进的技术,因为在k-匿名中虽然攻击者无法确定某个人到底是等价类中的哪条数据,但如果等价类中某项敏感属性值出现的频率过高,那么攻击者很有可能将这个人和这个属性值联系起来。所以L-diversity要求在同一个等价类中,某一项属性值的出现概率不能超过1/L,这样攻击者就不太可能将某个人和某个敏感属性值联系起来。但如果数据中敏感属性值比例过大,攻击者仍然有可能获得个人隐私。
1.3 基于数据失真的隐私保护技术
差分隐私[16-18]近年来被引入数据发布中的隐私保护,隐私保护模型旨在确保所有几乎相同的输入数据集之间的任何已发布数据具有相等概率,它保证了所有输出对个体不敏感。除此之外,即使攻击者拥有一定的背景知识,该模型也能使记录的隐私性得到有效保护[19]。
3 实现方法
通过数据实验对RDPk-means算法的可用性进行分析和说明。实验环境为:Inter(R) Core(TM) i3-2328M CPU@2.20GHz,8G内存,Windows7 64位操作系统,实验使用Java语言实现,采用的IDE开发工具为Eclipse,版本为Mars.2 Release (4.5.2)。算法中用到的数据来自于UCI Knowledge Discovery Archive database,具体信息如表1所示。
4 实验结果
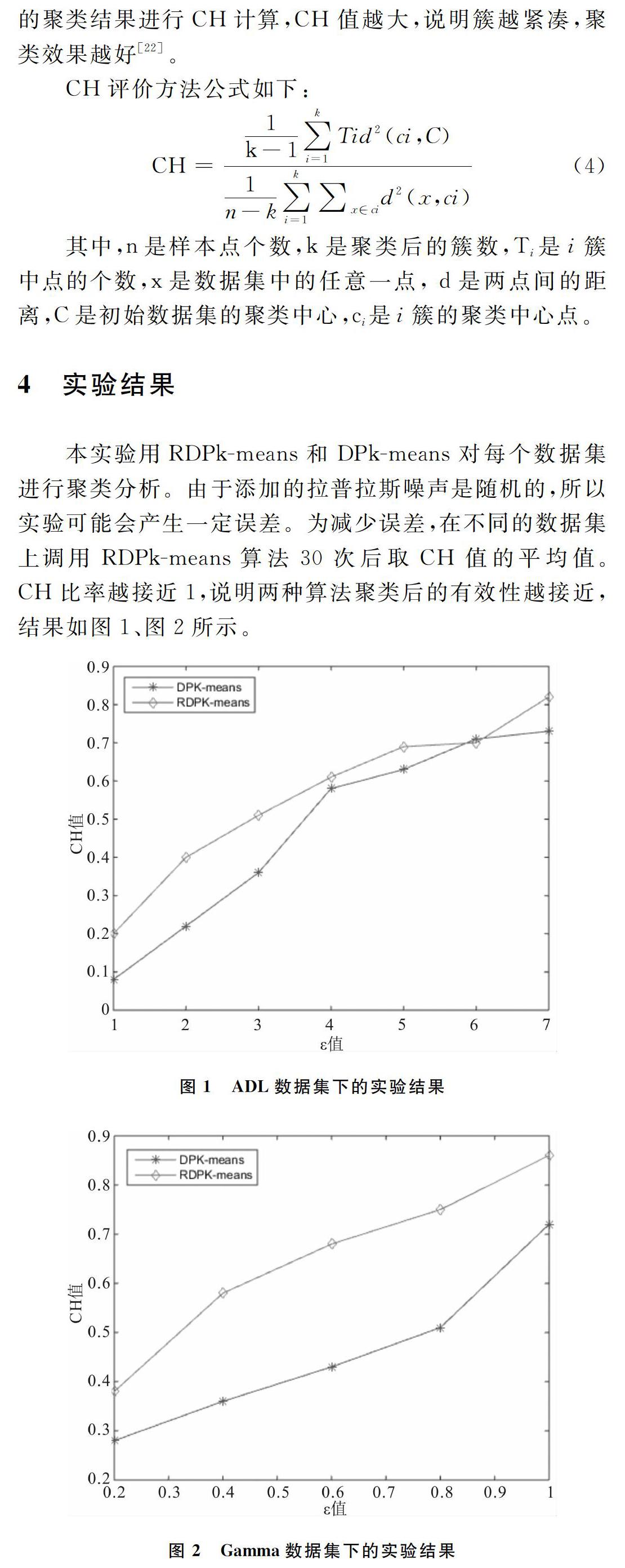
本实验用RDPk-means和DPk-means对每个数据集进行聚类分析。由于添加的拉普拉斯噪声是随机的,所以实验可能会产生一定误差。为减少误差,在不同的数据集上调用RDPk-means算法30次后取CH值的平均值。CH比率越接近1,说明两种算法聚类后的有效性越接近,结果如图1、图2所示。
从图1、图2可知,随着ε值的不断增大,CH的值最后也大大提高。这是因为通过改变初始点选择,提升了聚类中心精度,从而使聚类结果的偏差变小。尤其是当ε值较小、噪声较大时,RDPk-means算法聚类可用性提高;当ε值较大、添加噪声减少时,显示数据可用性逐渐接近原始K均值算法的聚类,这表明了RDPk-means算法的优越性。
5 结语
为解决现有DPk-means算法中聚类结果效率不高问题,本文提出一种新的RDPk-means算法。通过对原始数据集进行基于网格密度的划分,明显减少了异常值对结果的影响。另外,该算法通过划分每个维度的数据生成初始聚类中心,改善了初始聚类中心的选择及聚类效果。
参考文献:
[1] 贺瑶,王文庆,薛飞.基于云计算的海量数据挖掘研究[J].计算机技术与发展,2013,23(2):69-72.
[2] 闫蒲.互联网社交大数据下行为研究的机遇与挑战[J].中国统计,2016(3):15-17.
[3] 刘雅辉,张铁赢,靳小龙,等.大数据时代的个人隐私保护[J].计算机研究与发展,2015,52(1):229-247.
[4] 王璐,孟小峰.位置大数据隐私保护研究综述[J].软件学报,2014,25(4):693-712.
[5] 王保义,胡恒,张少敏.差分隐私保护下面向海量用户的用电数据聚类分析[J].电力系统自动化,2018,42(2):121-127.
[6] 李黎明.基于网格的隐私保护聚类挖掘算法研究[D].福州:福州大学,2010.
[7] 阚莹莹,曹天杰.一种增强的隐私保护K-匿名模型——(α,L)多样化K-匿名[J].计算机工程与应用,2010,46(21):148-151,180.
[8] 谷汪峰,饶若楠.一种基于k-anonymity模型的数据隐私保护算法[J].计算机应用与软件,2008(8):65-67.
[9] 焦佳.社会网络数据中一种基于k-degree-l-diversity匿名的个性化隐私保护方法[J].现代计算机:专业版,2016(29):45-47,60.
[10] 张健沛,谢静,杨静,等.基于敏感属性值语义桶分组的t-closeness隐私模型[J].计算机研究与发展,2014,51(1):126-137.
[11] 周水庚,李丰,陶宇飞,等.面向数据库应用的隐私保护研究综述[J].计算机学报,2009,32(5):847-861.
[12] SWEENEY L.k-anonymity:A model for protecting privacy[J].International Journal of Uncertainty,Fuzziness and Knowledge-Based Systems,2002,10(5):557-570.
[13] SWEENEY L.Achieving k-anonymity privacy protection using generalization and suppression[J].International Journal of Uncertainty,Fuzziness and Knowledge-Based Systems,2002,10(5):571-588.
[14] Li N,Li T,VENKATASUBRAMANIAN S.t-closeness:privacy beyond k-anonymity and l-diversity[C].Data Engineering,2007.ICDE2007.IEEE 23rd International Conference on.IEEE,2007:106-115.
[15] MACHANAVAJJHALA A. l-diversity: Privacy beyond k-anonymity [C].Data Engineering,2006.ICDE'06.Proceedings of the 22nd International Conference on.IEEE,2006:24-24.
[16] DWORK C.Differential privacy in the 40th international colloquium on automata.Languages and Programming,2006.Dwork C.Differential privacy:a survey of results[C].International Conference on Theory and Applications of Models of Computation.Springer,Berlin,Heidelberg,2008:1-19.
[17] DWORK C,NAOR M,PITASSI T,et al.Pan-private streaming algorithms[C].ICS.2010:66-80.
[18] DWORK C.Differential privacy under continual observation[C].Proceedings of the forty-second ACM symposium on Theory of computing.ACM,2010:715-724.
[19] 李楊,温雯,谢光强.差分隐私保护研究综述[J].计算机应用研究,2012,29(9):3201-3205,3211.
[20] DWORK C.The differential privacy frontier[J].Tcc.2009(54 44):496-502.
[21] 李杨,郝志峰,温雯,谢光强.差分隐私保护k-means聚类方法研究[J].计算机科学,2013,40(3):287-290.
[22] CALISKI T,HARABASZ J.A dendrite method for cluster analysis[J].Communications in Statistics-theory and Methods,1974,3(1):1-27.
(责任编辑:杜能钢)
