基于通胀的最优投资-消费、闲暇和自愿退休问题
2018-10-29费为银
恽 珍, 费为银, 梁 勇
(安徽工程大学 数理学院, 安徽 芜湖 241000)
最优投资消费问题是金融学研究的重要方向之一, 早在1969年, 文献[1]针对连续时间情形下最优投资选择问题已经进行了研究, 文献[2]探究了值函数的闭型解, 并提出了最优投资-消费决策。
上述文献报道均是最优投资消费问题, 但在实际生活中, 人们可通过工作获得劳动收入, 还可合理地投资从而增加财富, 使得退休后的生活更有保障。 把收入、闲暇和退休引入模型才可使投资-消费组合模型更贴合实际。文献[3-4]考虑了劳动收入是随机情形时的消费、投资、闲暇和退休问题, 均采用鞅方法解决最优投资消费问题。 文献[5]在使用动态规划法解决投资消费问题时, 推广了文献[4]的结果, 并验证了鞅方法和动态规划法得到的解的等价性。 文献[6]运用α-极大极小期望CES(constant elasticity of substitution)效用模型, 研究了代理人的最优消费、闲暇、投资组合和退休选择的问题, 其中区别了含糊与含糊态度。 文献[7]考察了一个带有CES型代理人的最优投资消费、闲暇和退休选择问题, 代理人可通过消费和闲暇获得效用, 并在高于一个最低劳动时间后可以灵活地安排劳动和闲暇时间。 文献[8]研究了带有生存约束的代理人的最优投资消费、闲暇和自愿退休的问题, 运用动态规划原理, 给出了最优决策和值函数。 文献[9]考察了在Knight不确定下3种借款约束情形及保险和退休的最优消费投资决策。
通货膨胀(简称通胀)是一种无法避免的宏观经济风险。 面对通胀带来的压力, 许多管理人重新调整了投资组合, 许多学者也在原来的最优投资-消费组合的基础上, 考虑了通胀对投资-消费的影响。文献[10]证明了通胀对代理人的经济活动有重要的影响。 通胀会带来物价的上涨, 导致代理人可以购买的消费品减少, 消费效用降低。 因此, 代理人需通过减少消费、增加投资来应对通胀。 文献[11]研究了消费篮子价格完全可观察和部分可观察两种情况的通胀环境下的最优消费和最优投资决策。 文献[12]考察了通胀环境下, 一个可投资于现金、名义债券和股票的幂效用投资者的最优资产配置。 文献[13]分析了在跳扩散环境下, 通胀因素和跳对投资者资产配置的影响。 文献[14]研究了投资者在通胀环境下带递归效用的最优消费和投资问题。 文献[15]基于连续时间均值-方差框架, 探究了通胀影响下投资终止时间不确定的最优投资组合选择问题.文献[16]运用了随机分析、动态规划原理和鲁棒控制方法,研究了在通胀和模型不确定下投资者的最优消费和投资组合问题。
为考察代理人在通胀环境下的最优投资-消费、闲暇和自愿退休问题, 本文在文献[17]的基础上引入了通胀因素, 运用动态规划原理, 通过求解优化问题值函数所满足的Hamilton-Jacobi-Bellman(HJB)方程, 获得值函数的解析解和关于投资-消费、闲暇和自愿退休的最优决策。
1 模型建立
在完备的金融市场中, 设(Ω,F,{Ft}t≥0,P)为一个带有Wiener过程W(t)的带流概率空间, 代理人可以将财富投资于两种资产:一种是名义利率为R的无风险资产, 如债券;另一种是预期收益率为μs和波动率为σs>0的风险资产, 如股票。无风险资产名义价格BN(t)与风险资产名义价格SN(t)分别满足式(1)和(2)。
(1)
(2)
居民消费价格指数(CPI)是度量通胀的重要指标,其是衡量所选定的一篮子消费品购买价格的指数。 文献[10]中投资者的消费篮子指代几种消费品及其权重。 本文为了简化, 忽略了多维的情况, 直接考虑消费篮子中物品价格的加权和, 即消费篮子价格。 消费篮子价格的动力学表达式如式(3)所示。
(3)
式中:μp为预期通胀率;σp>0为波动率。
设XN(t)为代理人在时刻t的名义财富量,πN(t)为代理人在时刻t投资于风险资产的名义资金额, 则XN(t)-πN(t)为代理人投资于无风险资产的名义资金额,cN(t)为代理人在时刻t的名义消费率, 且cN(t)>0,wN(t)为名义工资率。

(4)
且名义财富过程满足

(5)
设Xt表示代理人在时刻t的真实财富量, 则
根据伊藤公式可得
(6)

考虑到模型简化和代理人心理, 假设真实工资率为常数w; 不受通胀的影响, 则名义工资率满足wN(t)=w·P(t)。
真实财富过程满足
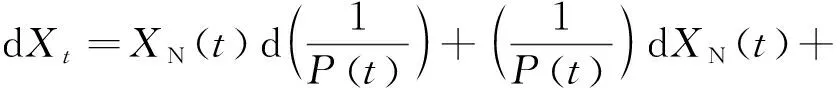
(7)
式中:X0为零时刻财富水平;x为零时刻财富水平的具体数值。
设BN(t)为代理人在时刻t的名义无风险资产价格,B(t)为代理人在时刻t的真实无风险资产价格, 则

(8)
(9)
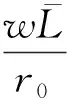
2 优化问题
为使消费和闲暇都能得到满足, 根据文献[3-4, 17]中定义的效用函数, 本文引入Cobb-Douglas效用函数,如式(10)所示。

(10)
式中:γ为相对风险厌恶系数;α为一个常数参数, 用来度量代理人的消费在就业阶段中的份额。若定义γ1: =1-α(1-γ), 则Cobb-Douglas效用函数可写为
(11)
期望折现效用的最大化为模型中代理人的目标, 则
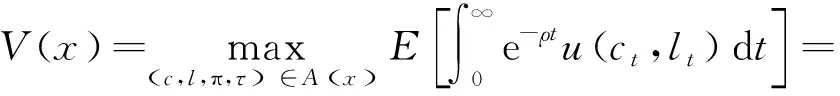
(12)
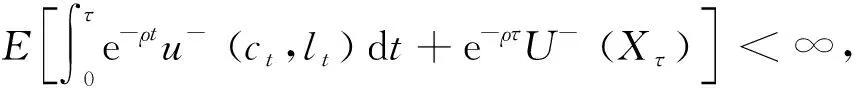
假设1
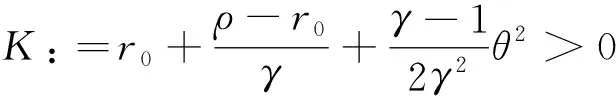
(13)
由于式(12)中退休后的值函数U(·)和经典Merton问题类似, 参照文献[17], 定义退休后的值函数为
定义二次方程为
(14)
该方程有两个根k+>0和k-<-1。
在假设1下, 值函数有如下表达式
命题1
(15)


(16)
(17)
(18)
(19)
(20)
(21)
(22)
(23)
证明: 退休前将控制变量l分为两部分: 闲暇率lt为一个控制变量, 闲暇率lt为常数L。
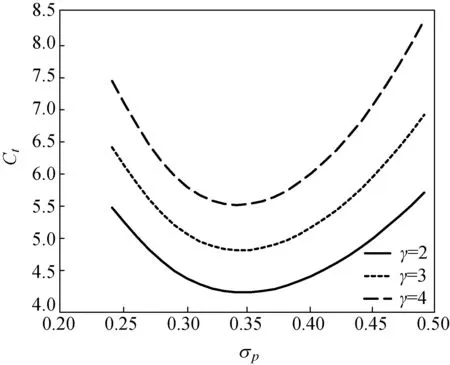
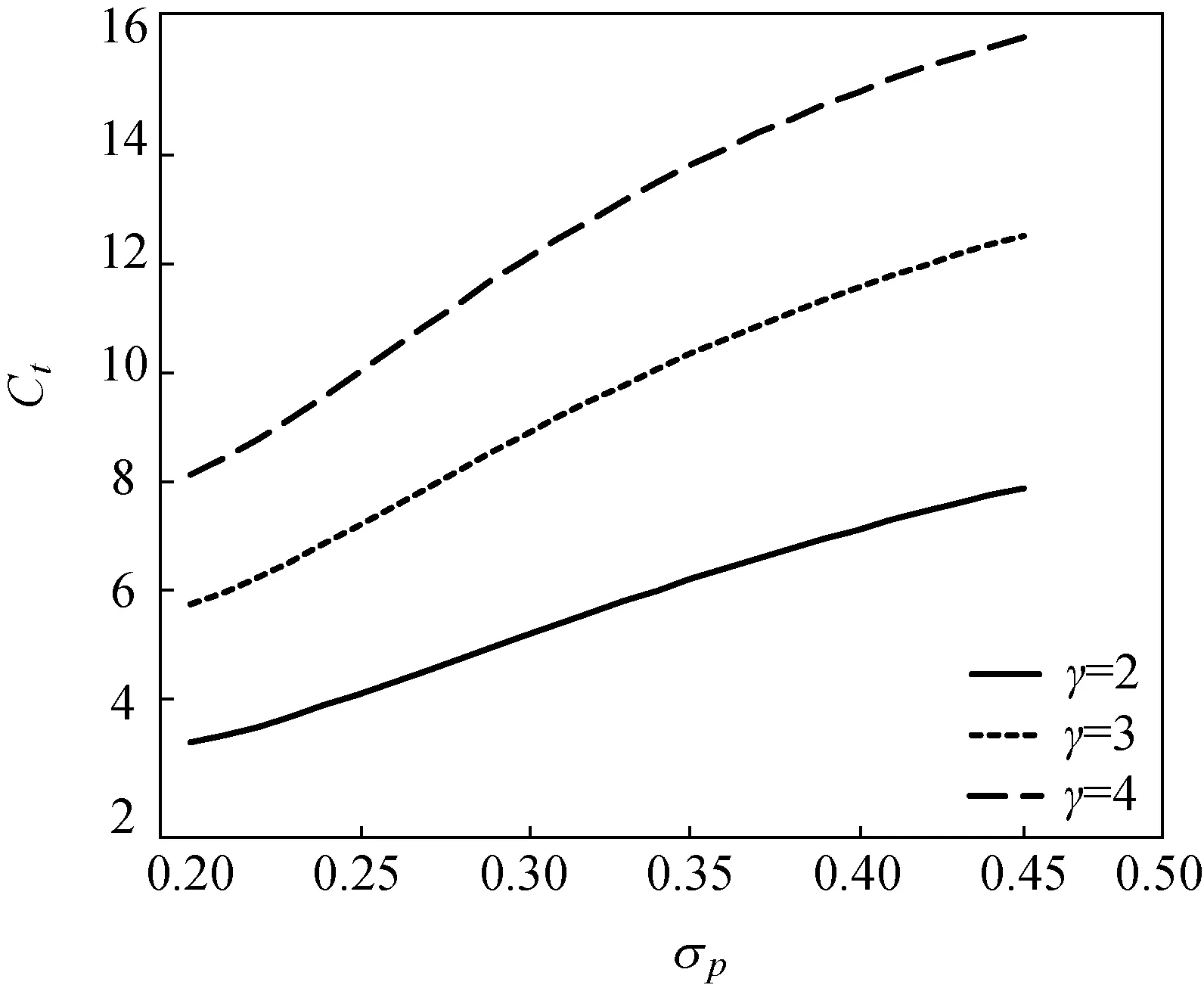
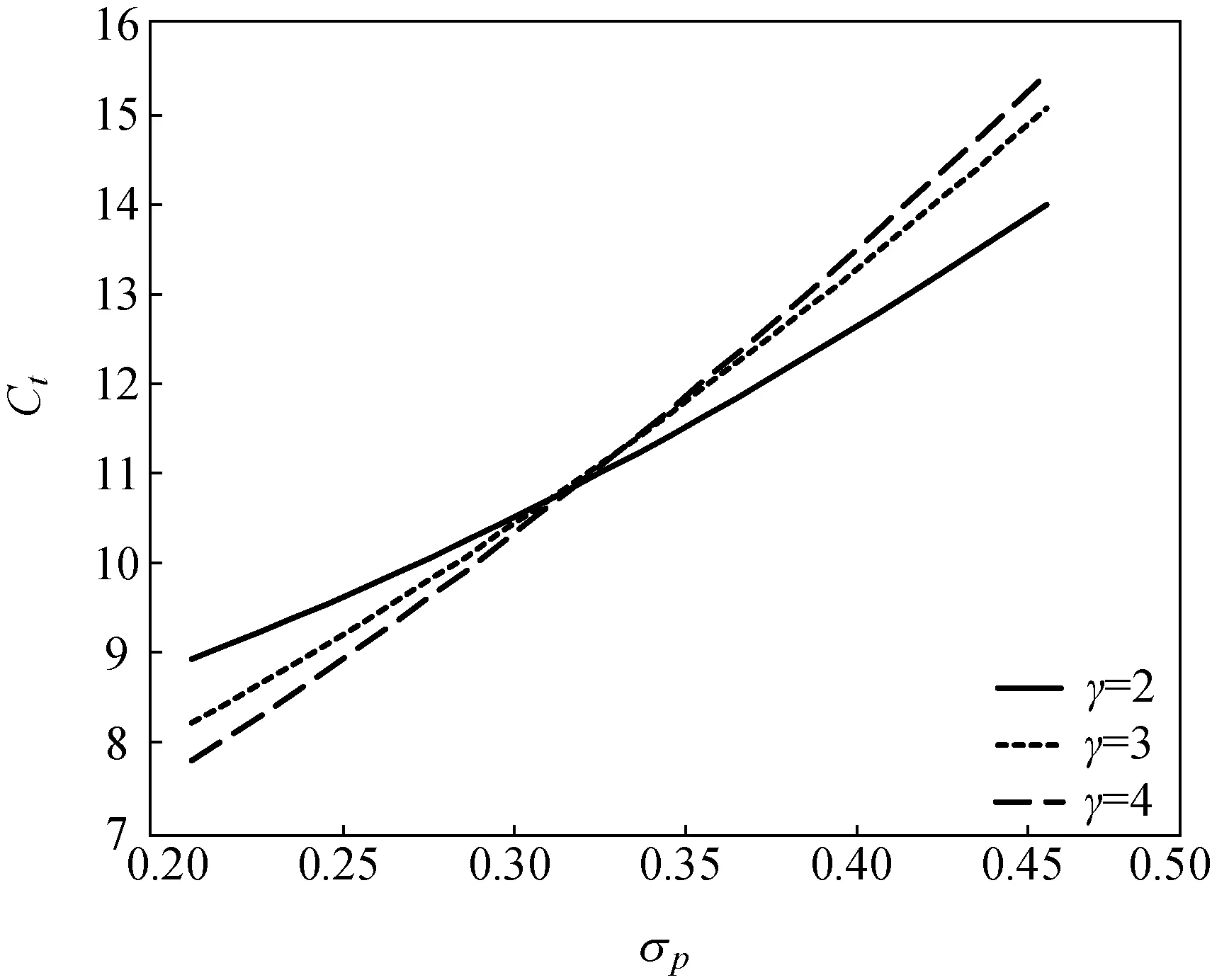
当0≤t<τ, 0≤l (24) 由一阶条件, 可得 (25) 将式(25)代入HJB方程(24), 可得 (26) 假设财富函数c=C(x),X(c)=C-1(x), 则 (27) 把式(27)代入式(26), 得 (28) 两边关于c求导, 得 (29) 式(29)的解如式(30)所示。 (30) 式中:k-<-1为方程(14)的一个根。 将式(30)代入式(28), 得 (31) 式中:ξ为式(22)的解. 当0≤t<τ,l=L时, 优化问题的HJB方程可写为 (32) 由一阶条件, 可得 (33) 同理, 可得式(32)的解和值函数如式(34)和(35)所示。 (34) (35) 式中:ζ为式(23)的解. 将式(30)和(34)求导, 代入上式, 得 (36) (37) 即 (38) 由式(36)~(38)可知, 若可知B2, 则可求得式(18)中的B1和式(20)中的A2。 简化得 (39) 由式(34)定义 (40) 将式(39)代入式(40), 可得 (41) (42) 将式(39)代入式(42), 可得 (43) 由式(41)和(43)可得B2。 命题2 式中:ξ和ζ为式(44)和(45)的解。 (44) (45) 证明: 根据一阶条件(25)和(33), 可得定理中的最优消费、闲暇、投资决策。 根据命题1中的式(23), 可得代理人在时刻t的财富Xt, 证毕。 为更好地分析财富水平和通胀因素对消费与投资的影响, 本文结合文献[7-11]中的数据, 利用Matlab进行了数值模拟。 由图1可知:相对风险厌恶系数越大, 越厌恶风险的投资者消费相对更低, 可适当控制消费; 消费的整体趋势均是单调增加的, 这是由于随着财富的积累, 消费水平随之提高; 在财富水平达到[-40, -20]之间时, 出现了一个向上的跳, 这是由于第2阶段时, 代理人闲暇达到了退休前的最大且固定, 工作时间也相对固定, 收入稳定可增加消费。在第2阶段和第3阶段之间出现了一个向下的跳, 这是由于代理人已经退休, 没有了收入来源, 此阶段投资者更愿意将所持有的资产用于风险资产的投资, 以期获得更多的财富, 减少了消费。 图1 财富水平Xt对最优消费Ct的影响Fig.1 Effect of wealth level Xton optimal consumption Ct 图2 财富水平Xt对最优投资π的影响Fig.2 Effect of wealth level Xton optimal investment π 由图2可知:对风险更加厌恶的投资者, 会将更少的财富投资于风险资产上; 投资的整体趋势均是单调增加的, 这是由于随着财富的积累, 投资随之增加。在第1阶段和第2阶段之间出现了一个向上的跳, 这是由于在第2阶段代理人具有稳定的收入, 财富的逐渐积累使其可以增加投资。 在第2阶段和第3阶段之间出现了一个向下的跳, 这是由于代理人已经退休, 没有了收入来源, 增加投资会不利于未来的消费, 因此投资会出现一个大幅度的下降. (a)第1阶段 (b)第2阶段 (c)第3阶段图3 3个阶段通胀波动率σp对最优投资π的影响Fig.3 Effect of inflation volatility σpon optimal investment π of three stages (a)第1阶段 (b)第2阶段 (c)第3阶段图4 3个阶段通胀波动率σp 对最优消费Ct 的影响Fig.4 Effect of inflation volatility σp on optimal consumption Ct of three stages 由图3(a)可知, 随着通胀波动率的增加, 投资先增加后减少。 投资先增加的原因:一方面是通胀刚刚出现, 代理人心理上认为市场的预期走势好, 增加投资可以增值保值; 另一方面是此阶段代理人的收入不是固定的, 如果某个时刻的投资出现亏损, 可通过减少闲暇、增加工作来增加收入,弥补亏损。 之后投资下降是由于通胀波动率的增加, 使得市场的不确定性增强, 代理人心理上更加担忧, 因此降低了投资。 由图3(b)可知, 随着通胀波动率的增加, 投资一直减少。 一方面是此阶段的收入没有前一阶段的高, 可用于投资的财富减少。 随着通胀波动率的增加, 市场越来越不稳定, 代理人更加担心投资亏损。另一方面是此阶段收入是个定值, 如果某个时刻的投资出现亏损, 代理人不能通过调节收入弥补亏损。因此第2阶段投资呈现下降的趋势。 由图3(c)可知, 此阶段随着通胀波动率的增加, 投资一直增加。这是由于退休之后, 财富有一定的积累, 但不会再有收入来源, 需要增加投资从而获得收益. 由图3可知, 相比于对风险厌恶更高的代理人,对风险厌恶更低的代理人而言, 无论在哪个阶段, 其投资都会更高。这是由于其会认为市场预期走势好, 将财富更多地投资在风险资产上可获得更高的收益. 由图4(a)可知, 随着通胀波动率的增加, 消费先减小后增加。消费先减小的原因:一方面是此时投资增加的原因另一方面是从消费者的心理来看, 通胀刚刚出现, 消费欲望降低, 导致财富购买力的下降。 之后消费增加的原因:一方面是市场波动越来越大, 代理人不愿进行更多的投资, 用于消费的资金将会更多; 另一方面是当通胀出现时, 相同的货币量消费越晚买到的东西越少。 代理人可能提前消费, 提前消费使等量货币价值最大化, 因此消费会增加。 由图4(b)可知, 消费水平随着通胀波动率的增加而增加。 这是由于在这个阶段投资随着通胀波动率增加而减小, 而代理人在此阶段收入是个定值, 可以适当地增加消费。 由图4(c)可知, 这个阶段消费随通胀波动率增加而持续增加, 这是由于退休之后, 代理人已经积累了一定的财富, 可以承担更高的消费 由图4可知,相比于对风险厌恶更高的代理人,对风险厌恶更低的代理人而言, 无论在哪个阶段, 其消费都会更低。这是由于此时的代理人已经将更多的财富投资在风险资产, 进而消费水平降低。 本文在通胀环境下建立模型, 推导了通胀折现后的财富过程。将代理人的生命周期依据闲暇率分为3个阶段, 在每个阶段建立相应的HJB方程, 求解方程后得出关于投资-消费、闲暇和自愿退休时间的最优决策。数值模拟分析表明, 消费和投资均随着财富水平增加而增加, 在面对变化的通胀波动率时, 代理人为了减小风险、增加收益, 在不同的阶段会选择不同的最优投资消费策略。总体而言, 适当的通胀会刺激投资和消费。

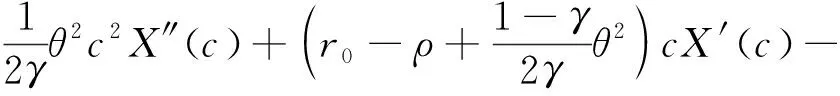















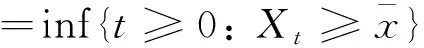
3 数值模拟与经济学分析
3.1 财富水平对消费和投资的影响



3.2 通胀波动率对消费和投资的影响




4 结 语
