自动换道系统最小安全距离研究*
2018-10-29吴杭哲刘斌刘枫
吴杭哲 刘斌 刘枫
(中国第一汽车集团有限公司智能网联开发院,长春 130011)
主题词:智能车 自动换道 最小安全距离
1 前言
红旗轿车是国内最早一批实现智能网联功能产品化的整车品牌:早在2013年就率先推出了具备自动紧急制动(Automatic Emergency Braking,AEB)、自适应巡航控制(Adaptive Cruise Control,ACC)等L1级自动驾驶功能的产品红旗H7;2018年即将推出具备L2级自动驾驶功能的产品,如全自动泊车(Auto Parking Assist,APA)、高级自适应巡航控制(Super Adaptive Cruise Control,SACC)等;2020年,搭载L3级自动驾驶功能的红旗汽车将具备高速公路自动驾驶和拥堵自动驾驶两项代表性功能。其中,自动换道功能开发将是L3级自动驾驶实现的关键路径。著名的图像处理公司Mobileye专门针对安全距离提出了责任敏感安全(Responsibility Sensi⁃tive Safety,RSS)模型,并将其作为公司未来重点技术之一进行部署。特斯拉Autopilot曾在2017年宣布推出自动换道功能,但至今仍未实现。究其原因,作为L3级自动驾驶代表性技术的自动换道的面市,需攻克两个重要问题:包含换道时机及安全策略等在内的自动换道逻辑设计;自动换道实施过程中的规划和跟踪方法实现。
本文针对自动换道逻辑设计进行研究。换道时机设计的关键是车辆换道过程中的最小安全距离,国内外的研究大多只考虑了直线道路车辆换道的最小安全距离模型。车辆换道时应首先检测车辆行驶的周围环境,检查是否有其他车辆或障碍物影响车辆的换道行为,如果车辆周围有静态或者动态物体,应检测出车辆与物体间的实时距离。文献[1]考虑车辆与前方的慢车是否有足够的换道距离,向左或者向右能否实现换道,当满足这两个条件时才实施换道行为;文献[2]考虑车辆与前、后紧邻车辆之间的距离,在此距离内进行安全换道所需的加速度能否满足车辆的稳定性和舒适性要求,若满足则进行安全换道;文献[3]、文献[4]在单向双车道环境下,考虑直线道路上车辆换道时的运动轨迹,分析为避免发生碰撞,安全换道时最小安全距离的临界值,以此界定换道距离的安全区域和非安全区域。但工程开发实践中,基于简单的直线道路安全距离模型无法涵盖车辆间复杂的位置关系和交通状况,为此,本文构建了两种安全距离模型:弯道工况最小安全距离模型,需要充分考虑道路曲率特点以及在本车换道前预估的碰撞风险情况;极限行驶工况最小安全距离模型,综合考虑两车极限运动条件以及本车换道过程中存在碰撞风险的情况。最后,在红旗H7轿车仿真模型上对比上述模型与传统直线道路上车辆换道最小安全距离模型,证明了模型的有效性。
2 弯道工况最小安全距离模型
2.1 模型的建立
现有研究中针对直线道路双车道已搭建了换道最小安全距离模型[3],车辆换道环境模型如图1所示,其中C0为换道车辆,C3与C4分别为初始车道前、后车辆,C2与C1分别为目标车道前、后车辆。文献[3]中以避免发生碰撞的临界条件为基础,推导换道车辆与周围紧邻的4辆车的最小安全距离S(0)C3、S(0)C4、S(0)C2、S(0)C1,即为避免换道过程中发生任何形式的碰撞,换道初始时刻C0与其他车辆的最小距离。

图1 直线道路车辆换道环境模型
为模拟高速公路场景,本文在此基础上构建了车辆曲率换道模型,如图2所示。该模型的基本前提是假设两条车道的中心线具有相同的瞬心,设外侧车道的曲率半径为R,车道间距为d。

图2 车辆弯路换道环境模型
车辆换道时,初始车道前、后车辆与目标车道前、后车辆对换道车辆影响最为直接。设C0为要进行换道的车辆,在初始车道上;C1和C2分别为目标车道上,换道结束后在C0后方、前方的紧邻车辆;C3和C4分别为换道前在C0前、后方的紧邻车辆。考虑到交通事故成因中侧面碰撞是仅次于正面碰撞的事故形态,占比较高,为此,本文将换道过程中研究对象锁定为C1和C2,将C3主要纳入AEB系统考虑范畴,C4可能与C0发生追尾事故时,可由C4采取制动或紧急制动措施,对C0一次换道行为的规划与控制影响较小,关于C0未完成换道需要返回本车道的情况本文暂不考虑。
2.2 C0与C2最小安全距离模型的建立
C2与C0发生碰撞的位置关系如图3所示,C0在C2后方可能发生的碰撞类型包括斜向碰撞、斜向刮擦或追尾碰撞[5],C0的左前角首先经过并与C2交于点C,在点C处或C0经过点C后,C0可能与C2发生碰撞。
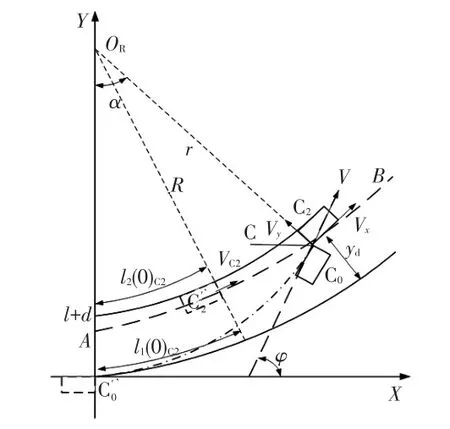
图3 C2与C0发生碰撞的位置关系
考虑到可能的碰撞形式,C0与C2不发生碰撞的条件为:
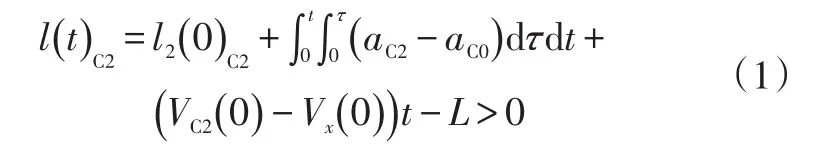
式中,l2(0)C2、l(t)C2分别为初始时刻和换道过程中任意时刻C2与C0沿内车道的圆弧距离,C0在C2后方时为正,反之为负;Vx(0)为C0的初始速度;aC0为 C0的加速度;VC2(0)为C2的初始速度;aC2为C2的加速度;L为车身长度。
由图3,根据几何关系可得:

式中,l1(0)C2为初始时刻C2与C0沿外车道的圆弧距离。整理得,C0和C2初始时刻沿圆弧的安全距离满足:

因此,为避免发生碰撞,初始时刻圆弧距离最小值为:
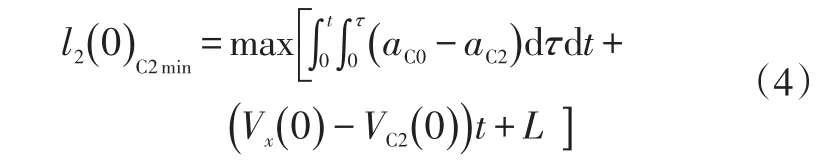
根据几何关系可知,换道初始时刻C0与C2的最小安全距离为:
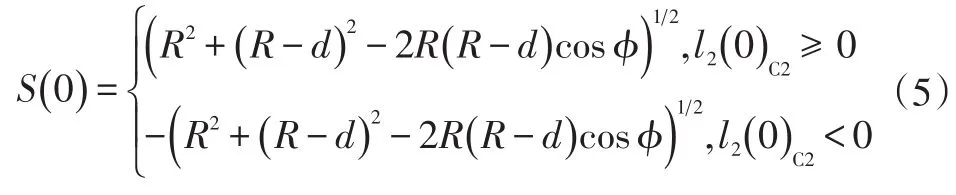
式中,ϕ为初始时刻C2与C0沿内车道的圆弧所对应的圆心角,可以由l2(0)C2表示为:

当道路曲率不为零时,记ΔS=l∞(0)-S(0)为直线道路与弯曲道路最小安全距离的相对差值。
可以看出,S(0)与两车初始时刻相对速度、相对加速度、换道时间、弯道曲率有关。
2.3 C0与C1最小安全距离模型的建立
与上述分析相似,C1为换道结束后目标车道上位于C0后方的车辆,考虑C0与C1发生碰撞的情况,位置关系如图4所示。

图4 C0与C1发生碰撞的位置关系
要求在换道结束后C0在C1前方,C1的初始速度较C0大,两车可能发生侧碰和追尾。
换道过程中,为避免发生侧碰,两车距离应满足:
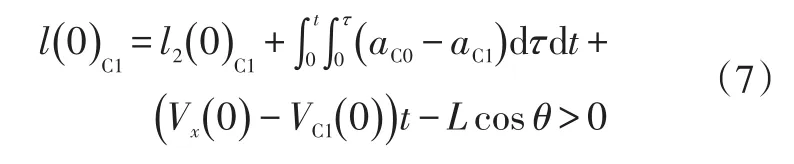
式中,l2(0)C1、l(t)C1分别为初始时刻和换道过程中任意时刻C1与C0沿内车道的圆弧距离;VC1(0)为C1初始速度;aC1为C1沿道路的加速度;θ为C0速度方向与车道切线方向所形成的夹角。
为避免发生追尾,两车距离应满足:

可以看出,当l(t)C1满足式(8)时,即可避免任何形式的碰撞,故初始时刻两车沿圆弧距离满足:
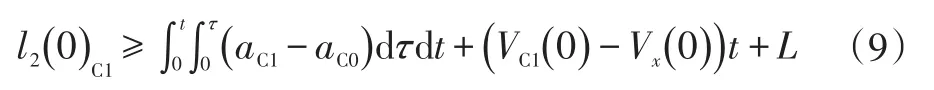
因此,为避免发生碰撞,初始时刻圆弧距离最小值为:
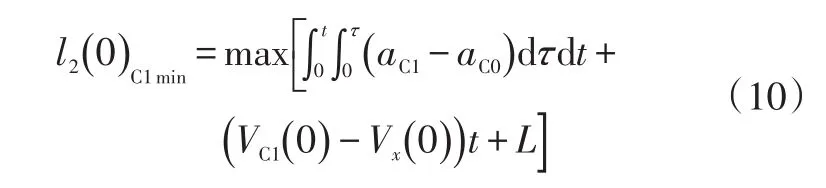
根据几何关系可知,C0与C1的最小安全距离为:

式中,σ为初始时刻所对应的圆心角,可以由l2(0)C1表示:

另外,C1与C2均为相邻车道上的车辆,因此C2与C0、C1与C0在直线道路上的换道安全距离和弯路换道安全距离的差值有相同的变化规律。
3 极限行驶工况最小安全距离模型
在上述讨论过程中,两车的运动状态均作了一定的限制和假设,并未考虑两车极端情况下的安全问题,本文分别从纵向和横向两个角度分析车辆极限行驶的安全要求。
3.1 纵向行驶极限工况
纵向行驶的极限情况如图5所示。假设车辆0和车辆1存在碰撞风险,在采取措施的t0时刻前,车辆0以其当前状态下可行驶的最大加速度a0xmax加速行驶,在t0后,前车以最大减速度d1xmax进行紧急制动,而本车执行最小减速度d0min制动,当达到两车接触点C时,纵向距离恰好为0,且纵向速度也为0。
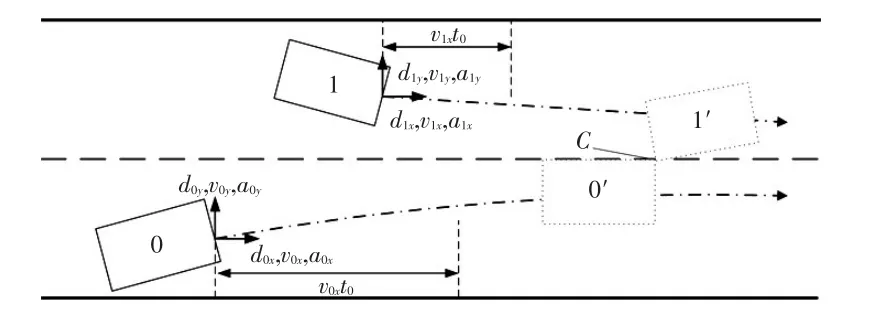
图5 极限行驶工况示意
设车辆0和车辆1的初始速度分别为V0x和V1x,则车辆0和车辆1极限工况下纵向安全距离为:
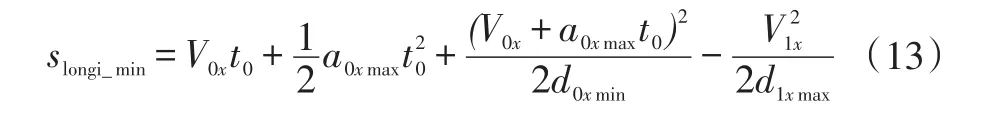
3.2 横向行驶极限工况
假设车辆0与车辆1存在碰撞风险,横向行驶的极限情况是:在采取措施的t0时刻前,均以最大横向加速度aymax加速行驶;在t0后,均以最小横向减速度dymin进行制动,当达到两车接触点C时,横向距离恰好为0,且横向相对速度也为0。
设车辆0、车辆1的初始速度分别为V0y和V1y,则车辆0和车辆1极限工况下横向安全距离为:

综上,两车行驶极限工况下的最小安全距离可以由两车的当前速度、加速度等推导得出,并且不受路面等几何条件的影响。
4 最小安全距离模型的仿真分析
使用红旗H7轿车数据作为本车和目标车模型:车身长度为5.1 m,车身宽度为1.87 m,实测的整车最大加速度a0xmax=5.6 m/s2(百公里平均加速度,峰值为8.7 m/s2),最大减速度d0max=11 m/s2,车道间距d=3.5 m。设本车初始速度为20 m/s,其他车辆初始速度为25 m/s。
4.1 C0与C2的最小安全距离仿真分析
以C0与C2相对速度ΔV=Vx(0)-VC2(0)和相对加速度Δa=aC0-aC2为变量,设道路曲率半径R=300 m,最小安全距离S(0)的变化情况如图6所示,直线道路和弯路上最小安全距离的差值如图7所示。

图6 C0与C2的最小安全距离
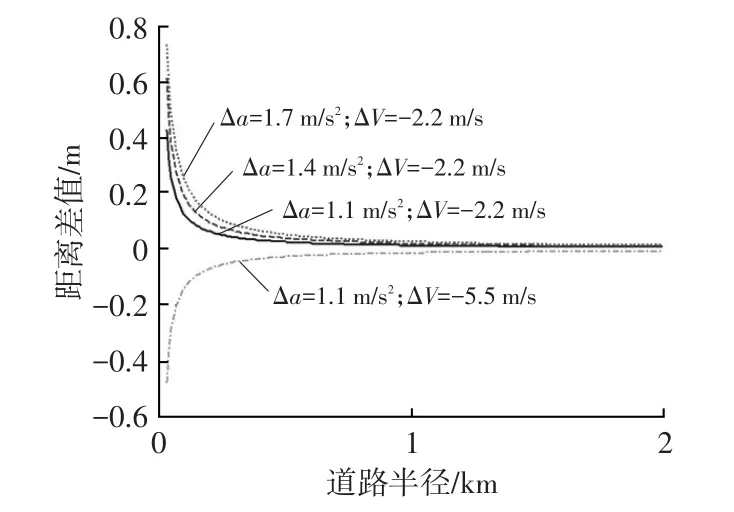
图7 直线道路与弯路最小安全距离的差值
图6中,最小安全距离曲面及其以上空间的各点满足安全换道条件。最小安全距离曲面由两个独立的曲面组成,中间断开处为-3.5 m<S(0)<3.5 m的区域,说明无论ΔV和Δa如何变化,S(0)的取值范围都不会在(-3.5,3.5)之间,这是因为S(0)表示初始时刻C0与C2左前端的最小距离,|S(0)|最小时,即为初始时刻两车并列行驶时,S(0)取值为初始车道与目标车道的间距。
由图7可以看出,直线道路和弯路上|ΔS|随道路半径变化有相同的变化趋势,即在城市道路上:当R较小时,|ΔS|较大,建议直线道路上的最小安全距离不能替代弯路上的最小安全距离,特别是在本车以较大加速度加速或本车初始速度较大时,若用直线道路上的最小安全距离替代弯路上最小安全距离,易发生剐蹭;当R增大时,|ΔS|逐渐减小;R→∞时,道路基本为直线道路,ΔS→0。
4.2 C0与C1的最小安全距离仿真分析
取道路曲率半径R=300 m,图8所示为C0与C1的最小安全距离的变化情况。

图8 C0与C1的最小安全距离
图8中,最小安全距离曲面及其以上空间的各点满足安全换道条件,其他分析与上节相似。
ΔS的变化趋势同C0与C2相似,R较小,或相对速度、相对加速度较大时,ΔS较大,随着R的增大,|ΔS|逐渐减小并趋于零。
4.3 极限行驶工况下最小安全距离分析
根据式(13)计算C0与C1在极限行驶工况下的纵向最小安全距离。本文采用文献[6]中满足正反梯形约束的横摆角加速度模型进行换道轨迹规划,换道时间5 s,车道间距为3.5 m,初始车速为60 km/h,换道后车速为80 km/h,为方便计算,可以认为紧急行动t0时刻前,C0进行匀加速运动,最大加速度a0xmax=1.11 m/s2,C1匀速行驶,车速为60 km/h,实施紧急措施t0时刻起,C1以舒适性最大减速度制动,d1xmax=3 m/s2。通过仿真,获得极限行驶工况下纵向最小安全距离与前车开始紧急操作的时间t0和本车最小制动减速度d0min的关系,如图9所示。
由图9可知,若本车可执行的最小减速度越大,换道开始后,前车采取紧急制动时机越早,即两车相对速度越小,极限工况下的纵向安全距离越短。当本车可执行最小减速度过小时,安全距离过大,不符合自动驾驶车辆对执行器与传感器的需求。仿真结果显示,为避免前车突然紧急制动导致碰撞,本车可执行的最小减速度为2.5 m/s2,换道未开始时,本车车速60 km/h,与前车的纵向最小安全距离为9.259 m,换道结束后,本车车速80 km/h,与前车的纵向最小安全距离为149.6 m。
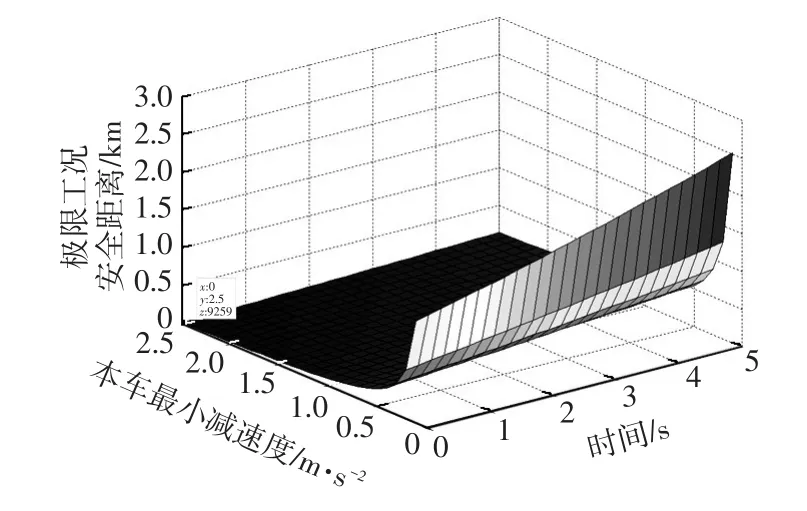
图9 极限工况纵向最小安全距离
在上述情况下,C0与C1纵向最小距离满足要求时,自动换道可不考虑横向最小安全距离。
当C0与C1无纵向相对运动,仅存在横向相对运动的情况下,根据式(14),计算C0与C1极限行驶工况下的横向最小安全距离。文献[6]中,本车C0在换道过程中的最大横向加速为1.12 m/s2,C1初始横向速度为0。为方便计算,可以认为紧急行动t0时刻后,均以最小横向减速度dymin进行制动。通过仿真,获得极限行驶工况下横向最小安全距离与前车紧急操作的开始时间t0和本车最小制动减速度d0min的关系,如图10所示。
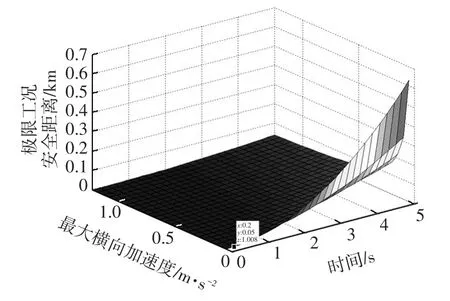
图10 极限工况横向最小安全距离
由图10可知,换道前,两车无横向相对运动关系,横向最小安全距离可不作考虑,换道执行后,若紧急行动后本车可执行的最小减速度越大,换道开始后前车采取紧急制动时机越早,极限工况下的纵向安全距离越短。
5 结束语
本文分别提出了基于弯道特征和极限行驶条件下两种最小安全距离模型,通过模型对比,基于路面特征的最小距离远小于极限行驶条件下的最小安全距离模型。前者主要考虑了当前状态下的两车运动状态和道路形态特征,未考虑车辆动力学的影响,代表车辆在理想车况、道路等条件下,可避免与相邻车辆剐蹭进行安全换道的情况下与其他车辆最小安全距离;后者主要考虑两车极限运动条件,忽略道路形态的影响,代表车辆在最恶劣的路面情况、整车执行状态等情况下,执行换道所需的安全距离,因而导致安全距离较大情况。两种模型为下一代红旗产品提供了思路:可提供两种换道模式供用户选择,即正常型模式(基于弯道工况模型)和保守型模式(基于极限行驶模型),最终的表现为前者的潜在事故风险较后者高,但后者换道的次数明显少于前者,自动驾驶车辆行驶效率降低,可能导致部分激进驾驶用户对自动驾驶的体验较差。
