Simulation of the overtaking maneuver between two ships using the non-linear maneuvering model ＊

Peng Du , A.Ouahsine , K.T.Tran , P.Sergent

1. Laboratoire Roberval, UMR-CNRS 7337 Sorbonne Universités, Université de Technology de Compiègne,Centre de Recherches Royallieu, CS 60319, 60203 Compiègne cedex, France

2. Cerema-134, Rue de Beauvais, CS 60039, 60200 Compiègne cedex, France

Abstract: The overtaking maneuver of two Esso Bernicia 1.9×105 DWT tankers was investigated using the system-based maneuvering method.The Brix model was incorporated to account for the overtaking interactions.Forces/moment acting on the ship hulls and maneuvering motions were analyzed for both ships during the overtaking.The influences of the speed ratio and the passing distance were specially studied.Two fitting formulas for the minimum distance during the overtaking were finally established as functions of the two factors respectively.They can be used to predict the minimum distance during an overtaking maneuver under similar conditions to avoid marine accidents.

Key words: Ship-to-ship interaction, maneuvering, overtaking, draught, yaw

Introduction

When ships move close to each other, the flow field around them will be changed and interactions caused by this approaching will act on the ships involved.Among these interactions, the overtaking maneuver is typical and has attracted much attention of researchers and engineers.When the overtaking happens, the original vessel trajectories and movements will be disturbed and the vessels may become unstable.This brings additional difficulties for maneuvering tasks and can be dangerous if not be properly controlled.A ship being overtaken may turn to the course of other ships.The accelerated fluids between ships will cause a pressure drop and impose attraction forces on the ships around, leading to the approaching or even collision of ships.Thereby understanding the overtaking process can be significant to prevent such marine accidents.

Many studies have been carried out for the overtaking phenomenon and several formulas have been put forward for its calculations[1-3].Brix[1]developed semi-empirical equations to estimate the maximum values for the longitudinal force, lateral force and yaw moment respectively, where the water depth was not considered and the ship length ratio was limited.Vantorre et al.[2]conducted extensive tests of ship-ship interactions in the towing tank in shallow water using four ship models with varied lateral distances, speeds, draughts and water depths.General rules of ship-ship interactions were concluded and formulations predicting the extreme values of interaction forces and moment were proposed based on the experimental data.Varyani[3]developed a generic mathematical model taking a complete set of factors into consideration, including shallow water effect, separation distance, ship length ratio, ship speed ratio, etc.But this model lacked the expression for longitudinal force coefficients.It has also been proven that Varyaniʼs model failed to predict identical forces when identical ships proceeded on parallel courses.

Numerical methods have been used for ship to ship interaction problems.Early methods such as the thin ship theories and slender-body theories[4]introduce limitations for the shipʼs geometry, where real ships are generally not thin or slender enough.Potential-flow theories have been developed for a long time and are still the most important computational fluid dynamics (CFD) methods for ship simulations.Rankine source method[5-6]and 3-D translatingpulsating source method[7]have been utilized for ship-ship interactions in narrow and shallow waters and seakeeping problems.As the most important viscous flow solver for marine applications, Reynolds averaged Navier-Stokes (RANS) method[8-11]is also adopted in recent years.Most of these works studied the ships traveling parallel with constant forward speed.The changes of ship motions under ship-ship interactions were neglected, limited by the numerical techniques and computational capabilities.The solving of the body motion equations and the update of the mesh displacements are extremely timeconsuming.Large mesh numbers have to be designed to obtain good accuracy, and even more meshes have to be used to identify the wave elevations at the free surface area.Compared with direct simulations using CFD methods, system-based maneuvering simulations based on mathematical models are time-saving[12].The kinetic parameters, ship trajectories, yaw and velocity changes, etc.can all be captured in a simpler way.The environmental forces and ship-ship interactions can also be included by incorporating them into the maneuvering equations[13-14].The results can be satisfactory as long as the formulas selected and the parameters provided are accurate enough.It is worth mentioning that the hydrodynamic coefficients used in the system-based method are derived from experiments or CFD.

In this paper, the overtaking phenomenon of two identical ships is investigated using the system-based maneuvering method, and the Brix model is implemented to calculate the overtaking interactions.Extensive simulations are conducted with various speed ratios and passing distances.The hydrodynamic and overtaking forces/moment, ship trajectories, yaw angles, etc.are analyzed to characterize ship maneuvering motions.Formulas for predicting the minimum distances during the overtaking are also proposed to prevent possible maritime accidents.

1.Nonlinear maneuvering equations

Actual ship motions take place in 6-DOF.They can be described using the equations of motion according to the rigid body kinetics.These equations can be expressed in a compact form as[13]

whereMRBis the mass matrix,CRBis the Coriolis and centripetal matrix due to the rotation,vis the velocity vector andτRBis the vector of external forces and moments.

Ship maneuverability refers to the ability of a ship to keep or to change its motion under control actions.For simplicity, the heave, roll and pitch motions are neglected, the ship maneuvering model(Eq.(1)) can then be formulated as a coupled surge-sway-yaw model (Fig.1).This leads to the 3-DOF model given by:

wheremis the mass of the ship,Izis the moment of inertia aboutzaxis, (xG,yG) is the position of the gravity center, (u,v,r) are the linear and angular velocities.(X,Y,N) are the forces and moment acting on the ship, which are always non-dimensionalized during the maneuvering simulations.In this study, their dimensionless forms are calculated using[15]:

wheregandLare the gravitational acceleration and ship length between perpendiculars.

Fig.1 Definition of the coordinate system and kinematic parameters

By taking the midship pointOas the origin(Fig.1), the reduced maneuvering equations can be expressed as:

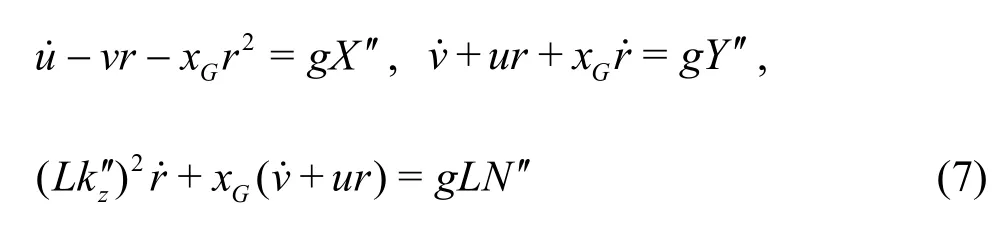
whereTpis the propeller thrust,ζis an additional term for the shallow water effect,cis the flow velocity at the rudder andδis the rudder angle.

Table1 Parameters of the Esso Bernicia 1.9×105DWT tanker

In this study, the Esso Bernicia 1.9×105DWT tanker (Table1) is selected, whose expanded hydrodynamic forces and moment of Eq.(8) can be written as[16-17]:

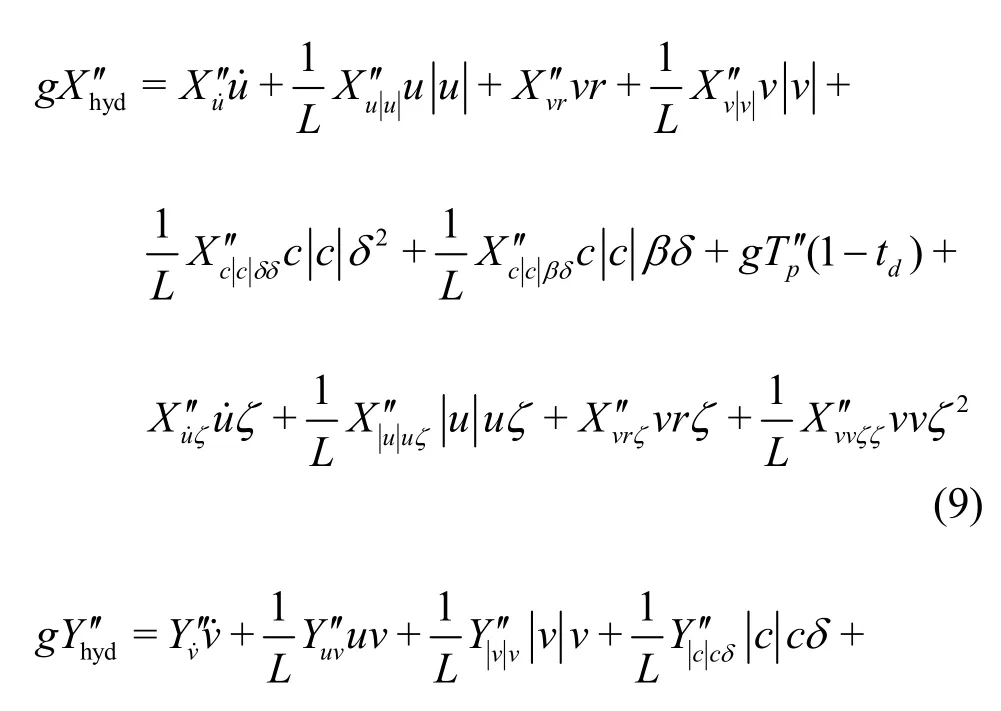
2.Formulation of overtaking models

The ship overtaking models can be incorporated into the maneuvering equations (1) and (7) as:

Fig.2 Schematic presentation of the ship overtaking and coordinate system

Several models[1-3]have been established to formulate the interactions during the ship overtaking(Fig.2) as described in the Introduction.Since this study focuses on the overtaking of two identical ships,the model of Brix[1]will be adopted and incorporated into the maneuvering equations for further investigations.This model can estimate the longitudinal force, lateral force and yaw moment at the same time.It has been shown[18]that the Brix model provides reasonable results, except for the surge force coefficients, which seem underestimated.The equations for the maximum values are as follows:

with the coefficients:

whereLm=1/2(Ls+Lf) is the mean ship length,Tm=1/2(Ts+Tf) is the mean draught andum=1/2(us+uf) is the mean speed, with the subscripts“s” and “f” denoting the slower ship and the faster ship (Fig.2).WhenLf/Ls≤ 1 .5, larger coefficients should be used, and vice versa.yccis the passing distance between two ships.The values in Eq.(14) are valid for a standard passing distanceyccret=0.35Lm.

Then the forces and moment during the overtaking can be calculated as:

where the non-dimensional coefficientsXα,Yα,Nαare functions of the relative ship positionξ=xcc|Lm(Table2).The forces/moment in Eq.(15) will be first non-dimensionalized using Eq.(6) and then incorporated into the maneuvering equations (12).

Table2 Forces and moment coefficients as a function of the relative ship position for the Brix model[1]

Table3 Hydrodynamic coefficients of the Esso Bernicia 1.9×105 DWT tanker[15]

3.Model tests and validations

3.1 Turning circle tests

In this section, the accuracy of the maneuvering equations (9)-(11) is tested and the validation of the system-based maneuvering is done using the turning circle tests.Regarding the hydrodynamic coefficients,in order to reduce the error between the calculated and experimental data, we have adopted the optimized values (see Table3) obtained in our previous study[15],instead of the original values.During the optimization,a sensitivity analysis for the hydrodynamic coefficients is first carried out to select the most significant ones.Then these coefficients are optimized using traditional optimization techniques, such as the sequential quadratic programming (SQP), the Broyden-Fletcher-Goldfarb-Shanno (BFGS) algorithms, etc., according to the experimental trajectories.Detailed procedures can be found in Refs.[15, 19].

Conventionally, the turning circle, zigzag, spiral maneuvers, etc.are performed to evaluate shipʼs controllability and maneuverability.In the present study, the turning circle tests are conducted for preliminary validation.Parameter settings are listed in Table4.

Table4 Simulation parameters of turning circle tests

Fig.3 Comparison between simulated and experimental[20] trajectories in turning circle tests

Figures 3, 4 show the comparisons between computed and experimental data.It can be seen that the simulation predicts correctly the ship trajectory with small deviations.The cumulative difference of ship positions in Fig.3 is less than 10 m.The surge velocity and yaw angle in Fig.4 are also in accordance with the experimental results.

3.2 Ship overtaking tests

Fig.4 Comparison between simulated and experimental[20] surge velocities and yaw angles in turning circle tests

Table5 Simulation parameters for the ship overtaking tests

Tests of the overtaking maneuver are also carried out to confirm the validity of our method.Simulation parameters are selected as shown in Table5.Since the Brix approach is only applicable in deep water, the water depths in our simulations are set to 200 m(h|hd=10.8).The overtaking process of both ships in our simulations is concluded as follows:

When the faster ship catches up with the slower ship (ξ≥ -1,ξ=xcc|Lm), the ship-ship interaction occurs which gives rise to the modification of the trajectories and motions of both ships (Figs.5-7).The interaction forces and moment as functions of the relative ship positionξare recorded as shown in Fig.8.It can be observed that the overall process can be divided into two stages by the position where the two ships move abreast (ξ=0).At this position, the long-itudinal force and yaw moment of the overtaking effect reduce to zero, while the lateral force reaches the maximum value.This attraction will cause an unsafe lateral approaching between the two ships which could cause maritime accidents, if not well controlled.The overtaking effect will also cause the change of hydrodynamic forces and moment.This change tends to resist the overtaking effect and reduce the total forces and moment acting on the ship hull.

Fig.5 (Color online) Ship trajectories during the overtaking maneuver

Fig.6 (Color online) Surge velocities during the overtaking maneuver (ξ= xcc |Lm)

Fig.7 (Color online) Yaw angles during the overtaking maneuver (ξ= xcc |Lm)

Fig.8 (Color online) Overtaking, hydrodynamic and total forces and moment acting on the ships during the overtaking maneuver.(a), (c), (e) correspond with the slower ship, (b), (d), (f) the faster ship.ξ = xcc |Lm

Fig.9 (Color online) Overtaking forces and moments acting on the ship hull for various initial speed ratios.(a), (c), (e) correspond with the slower ship, (b), (d), (f) the faster ship.uf and us are the faster and slower speeds respectively.ξ = xcc |Lm

When the midship section of the faster ship is behind that of the slower ship (ξ＜0), the longitudinal force drags the slower ship and speeds up the faster ship (Fig.6).Velocities of both ships in Fig.6 reach the extreme value whenξ=0 because the longitudinal forces return to zero.The forces/moment here, if not specified, all denote the total ones as shown in Fig.8.The lateral force first repulses and then attracts the slower ship (Fig.8).The repulsion may be caused by the “pushing” of the faster ship transferred by the fluid.At the same time, the pressure drop between the two ships accelerates the water,imposing an attraction force on both ships.With the approaching of the faster ship, the attraction becomes dominant gradually, and reaches the extrema when the two ships move abreast (ξ=0).The lateral force mainly shows an attraction effect for the faster ship at this stage.In Fig.5, it can be seen that the trajectories of the slower and the faster ships are changed by the repulsion and the attraction effect respectively.In fact,according to the experiments of Vantorre[2], the lateral force should include two repulsion stages around bothξ= 1 andξ=-1 for the slower ship.This ignorance is also a drawback of the Brix model.The interaction between the bow of the faster ship and the aft of the slower ship imposes a positive yaw moment on both ships, inducing a “bow-out” effect for the slower ship and a ‘bow-inʼ effect for the faster ship(Fig.7).

When the midship section of the faster ship is in front of the midsection of the slower ship (ξ＞0), the longitudinal forces reverse, showing a drag for the faster ship and a thrust for the slower ship (Fig.6).The lateral forces are mainly an attraction except a final repulsion stage for the faster ship (Fig.5).The yaw moments also reverse, causing the yaw angles of both ships changing to the opposite direction (Fig.7).

According to the work of Vantorre[2], the ships in our work show correct behaviors.However,Vantorreʼs experiments were carried out in shallow water and their ships were fixed with limited motions of surge, heave and pitch.Confinement effects play important roles under these conditions, which makes the forces/moment in their work greater than ours.Therefore, our study can fairly predict the ship motions during the overtaking maneuver.

Table6 Simulation parameters for the cases with various initial speed ratios.uf and us are the faster and slower velocities respectively

4.Results and discussions

When a ship overtakes another, both ships should be controlled keeping a safe distance to avoid marine accidents.During the overtaking maneuver, ship speeds and passing distances are crucial factors.The two parameters are considered respectively to investigate their effects in this study.The minimum distances between the two ships are quantitatively formulated at last.

4.1 Influence of ship speeds

Fig.10 (Color online) Ship trajectories for various initial speed ratios

Fig.11 (Color online) Yaw anglesfor various initialspeed ratios ξ = xcc |Lm

The simulation parameters for this case are shown in Table6.The initial passing distance between the two ships are kept 100 m.The initial speed ratios uf/us=3,4,… ,8 are selected to cover a wide and realistic range, where ufand usare the faster and slower velocities respectively.A speed ratio less than 3 will cause the collision of two ships in our cases.The propeller revolution corresponds with each speed value.The water depth is set to 200 m to guarantee the deep water condition for the Brix model.

The forces/moment during the overtaking are shown in Fig.9.Only the overtaking forces/moment are plotted here for comparison.It can be observed that they increase with the augmentation of the speed ratio, which means that a small speed ratio is beneficial to decrease the overtaking interactions.However, the overtaking period will become relatively long with low speed ratios, which can be observed in Fig.10.When the speed ratio is high, the lateral force will deflect the ships from their original courses at the early stage.Then it will change its sign and drag the ships to the opposite direction.The faster ship is pushed away from the slower ship at last, while the slower ship is dragged towards the faster ship by the suction effect.Both ships turn to the starboard side at first because of the positive yaw moment (Fig.11).When the midsection of the faster ship passes that of the slower ship, the longitudinal force and yaw moment will change their directions.In Fig.11, the heading direction of the faster ship is totally reversed at last.When the speed ratio is too small, the overtaking forces/moment are not able to change the ship motions intensively, which is beneficial to the maneuvering of the ships.Actually, keeping a low speed is a common measurement during an overtaking maneuver.The ship maneuverability does not change dramatically under this condition and the motion change is easy to be counteracted by the rudder action.

For a safe overtaking, the distance between ships should not be too small, otheewise it may lead to the collision.Predicting the minimum distance during the overtaking maneuver is then critical to avoid marine accidents.In this study, the minimum distance is defined as the smallest value between the two trajectories at a certain moment.With our maneuvering simulations in this study, the minimum distances can be extracted and a model can be established as functions of the speed ratio.In Fig.12, the minimum distance increases with the growing of the speed ratio.Because when the speed ratio is large, the overtaking period will become relatively short.The ships will not have enough time to change their motions before they separate from each other.However, when the speed ratio is low, the minimum distance between the two boats appears late.Therefore, although a low speed ratio can significantly reduce the overtaking effect, the interaction duration is also increased, leading to a small minimum distance between ships during the overtaking.Therefore, in real situations, only decelerating the ship is not sufficient when the ships are too close to each other.Proper rudder actions are also needed to limit the ship turning.From the projected data on the “D-ξ” surface, it can be seen that the minimum distance always appears right after the faster ship passes the midsection of the slower ship.This period is then the most dangerous during the overtaking.

Fig.12 (Color online) Influence of the initial speed ratio on the minimum distance betw een ships.ξ = xc c /Lm .Do is the original data of the minimum distanc eas functions of ξ and u f /us .Dp1 and Dp2 aretheprojected data on the “D-u f /u s ” and “D-ξ” surfaces

Table7 Simulation parameters for the cases with different initial passing distances.uf and us are the faster and slower pee pctivy

The relation between the minimum distance and the speed ratio can be observed on the “D-uf/us”surface in Fig.12.The data is projected on this surface and then fitted to establish a formula

whereDis the minimum distance between ships,uf|usis the initial speed ratio.So the minimum distance shows a power law relation with the speed ratio.The coefficient of determination2(R) is 0.9998 (see Fig.12), indicating a good fitness of our data.

4.2 Influence of passing distances

The simulation parameters for this case are shown in Table7.In this case, the initial passing distanceycc, i.e., the lateral distance between the two ships before overtaking happens, is varied from 80-180 m with a constant initial speed ratio3.Other para- meters are kept the same as in the case of speed ratios.

In Fig.13, the overtaking forces/moment can be observed to decrease with the increase of the initial passing distance.With smaller initial passing distances, the large overtaking interactions will make the two ships deviate earlier and more from the original course (Fig.14).Although the trajectories are greatly changed, the overtaking distances keep nearly the same, indicating that compared with the initial passing distance, the speed ratio is a more important factor influencing the time and distance of the overtaking effects.The yaw angles also become larger withsmallerinitialpassingdistances (Fig.15).Dramatic changes can be observed for the faster ship because the ship heading is totally reversed by the yaw moment.And smaller initial passing distance makes this change more obvious.Thereby a large passing distance can reduce the overtaking effects,thus the maneuvering difficulties during the overtaking.

Fig.13 (Color online) Overtaking forces and moments acting on the ship hull for various initial passing distances.(a), (c), (e)correspond with the slower ship, (b), (d), (f) the faster ship.ξ = xcc |Lm

Fig.14 (Color online) Ship trajectories for various initial passing distances: In (a), the trajectories are moved to zero in y direction for comparison

Fig.15 (Color online) Yaw angles for various initial passing distances

As in Section 4.1, the minimum distances between the two ships are also extracted to characterize the effect of the initial passing distance in Fig.16.The minimum distance nearly appears at the same position (ξ=0).A fitting formula between the minimum distance and the initial passing distance is obtained as following

whereyccis the initial passing distance (see Fig.2).It can be seen that the two parameters show a linear relation.The coefficient of determination2(R) is 0.9999.

Fig.16 (Color online) Influence of the initial passing distance on the minimum distance between ships

5.Conclusions

The overtaking m5aneuver of two identical ships(Esso Bernicia 1.9×10 DWT tanker) was investigated by using the system-based maneuvering simulation and by incorporating the Brix model into the maneuvering equations.Maneuvering motions of both the faster and slower ships during the overtaking were successfully simulated, including the trajectories, yaw angles, interaction forces/moment, etc.The results showed that the longitudinal force and yaw moment changed their directions at the positionξ=xcc|Lm=0, while the lateral force reached its maximum at this position.The hydrodynamic interactions tend to resist the changes induced by the overtaking effects.But the overtaking interactions were more dominant.

Particular attention has been given to the influences of the speed ratio and the shipsʼ passing distance, because of their importance to the safety during the overtaking maneuver.Six initial speed ratios and passing distances were designed in this study.Small speed ratios and large passing distances were found to be beneficial to reduce the overtaking interactions.However, the overtaking duration will become relatively long.A speed ratio less than 3 will cause the collision of two ships in our cases.Rudder action should be executed to counteract this effect under this condition.Two fitting formulas of the minimum distance between the two ships were established as functions of the two factors respectively.The minimum distance showed a power law relation with the initial speed ratio, and a linear relation with the initial passing distance.According to the formulas,the minimum distance during the overtaking can then be predicted under similar conditions, which can be used to avoid marine accidents.