多级压裂水平井试井理论及产能评价

李 月，纪大伟，王 杰

（东北石油大学石油工程学院，黑龙江大庆163318）

随着工业的迅猛发展，对石油需求量的不断增加[1]，相对于水平井，直井开发过程中注水注驱油剂难度大、采收率较低[2-4]。因此，采用水平井进行生产[5]，为了使水平井增产，常采用压裂技术以保证裂缝与油层的充分接触，形成油气水渗流通道，从而使原油高效产出，因此对水平井压裂后的产能评价十分重要。

目前，国内外对油藏产能评价方面的研究相对较少，主要根据油气渗流理论、高等数学等知识，采用模拟法和解析法应用于产能评价[6-7]。模拟法主要包括数值模拟法和物理模拟法。数值模拟法主要针对气液两相流来研究水平井产能，现有的数值模型中对压裂水平井产能的预测和评价不够准确，需要进行深入的研究。物理模拟法通过建立物理模型，但是其模型较为理想化，不能更好地描述油藏复杂的储层环境[8]。解析法主要针对稳定单相流，利用数学理论，在Darcy公式的基础上，通过Green函数、点源函数、Laplace变换[9]和傅立叶变换，推导出压裂水平井的产能计算公式[10-12]。但是解析法误差较大，多用于求解简单情况的问题，应用范围不大，且目前适用于油藏的水平井产能公式并不适用于气藏。为此，本文通过建立多级压裂水平井试井分析模型，利用多级压裂水平井试井解释软件，快速、准确的对压裂水平井进行产能评价，为油田的高效开发提供依据。

1 理论基础

1.1 井筒储集和表皮效应考虑方法

受天然气所处的压力环境影响，气井在进行试井时，描述气层压力变化的偏微分方程演化成为压力的非线性方程，很难求出解析解。为此引入拟压力代替压力作为微分方程的变量，从而在形式上使气体微分方程与油水层关于压力的微分方程保持一致，以简化求解方程的过程。拟压力的表达式为式（1）：

式中，p为地层压力，MPa；p0为任意选取的参考压力点，通常取p0=0 MPa；ψ(p)为气体拟压力，MPa/MPa⋅s；μ(p)为地层气体黏度，MPa ⋅s；Z(p)为真实气体偏差系数，无量纲。

引入井筒储集和表皮效应到裂缝系统的Laplace空间不稳定压力公式[13]，即需要在Laplace空间推导一个新的压裂水平井系统解释模型时，可以先不考虑井筒储集效应和表皮效应，在不稳定压力公式推导出来后，加入井筒储集和表皮效应，使井筒引起的不稳定压力反应可以单独使用，便于试井解释模型的建立和组合分析。

对于压裂水平井，当考虑井筒井底储集和表皮效应时，不能使用传统的有效井径模型。

当不考虑表皮效应时，开始生产时t=0 h，应用Duhamel褶积定理，无量纲井底压降为式（2）：

对式（2）进行Laplace变换可以写成式（3）：

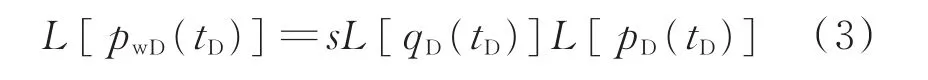
对式（3）进一步推导得到式（4）：

当考虑井筒储集效应时，无量纲产量qD的表达式如式（5）所示：

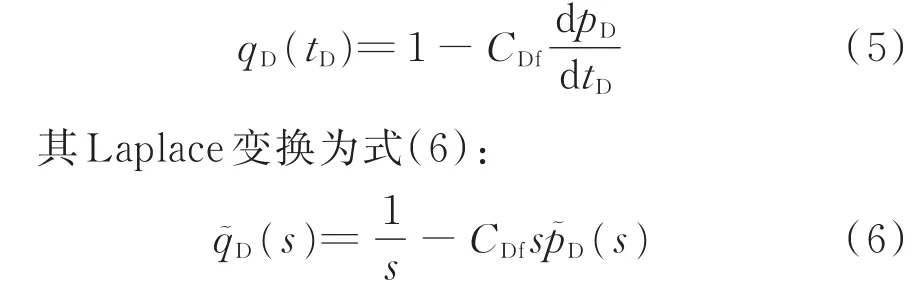
当考虑表皮系数时，对定产量压力响应，加上表皮系数，Laplace变换为：

将式（6）、（7）代入井底压力无量纲表达式（4）中，得到式（8）：

式中，pD为无量纲拟压力；tD为无量纲时间；qD为无量纲产量；CDf为无量纲井筒存储系数；S为表皮系数。

绘制无量纲拟压力及其导数曲线拟合图版，如图1所示。

图1 无限大油藏1条裂缝试井解释图版Fig.1 Interpretation chart of 1 fractured well test in infinite r eservoir

1.2 无限大油藏水平井多裂缝系统

1.2.1 物理模型 假设油藏无限大，水平井内压裂多条裂缝，且沿井筒方向压裂多条完全贯穿油层的垂直裂缝，仅在裂缝与井的交汇处产生压降，水平井仅在裂缝处射孔，物理模型如图2所示。图2中，n为裂缝条数，条；f1为井筒；xf为x方向条带源的宽度，m；yf1为y方向条带源的宽度，m；D为两条裂缝之间的距离，m。

图2 多裂缝压裂水平井物理模型示意图Fig2 Multi-fracture fracturing horizontal well physical model schematic

1.2.2 数学模型 首先采用Newman乘积方法求出相应的空间或平面点源解析式，然后在汇源分布区域内对此点源解析式进行积分，最后可得到问题的解[14-15]。对于无限大油藏单裂缝二维源函数，可用x方向条带封闭地层中宽为2 xf的条带源、y方向条带封闭地层中直线源两个瞬时源函数的乘积给出。

x方向条带源为式（10）：

根据Newman乘积，得出沿y方向产生的多裂缝直线源的二维源函数解析式为式（12）：

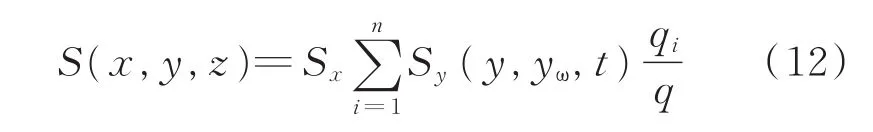
对式（12）进行积分，可得多级压裂水平井系统的压降表达式为式（13）：

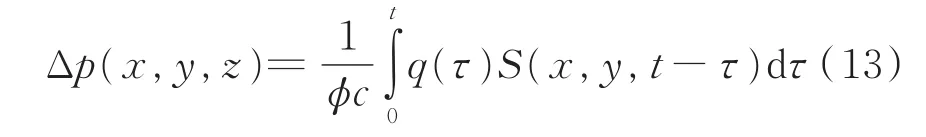
假设流体在水平井井筒与裂缝之间流动为无限导流，由于水平井内裂缝与井筒相连接，所以水平井井筒压降与裂缝处产生压降相同。再由水平井定产归一条件得式（14）方程组：

对式（14）进行求解可以得到井底压力及各裂缝沿井筒的流量分布。

2 实例应用

水平井X一共压裂4条裂缝，裂缝参数如表1所示。该水平井渗透率1.2×10-3μm2，井筒表皮系数0，井筒储存系数2.3，原始地层压力30 MPa，有效厚度5 m，孔隙度0.17，油井半径0.1 m，压缩系数0.000 2，体积系数 1.1。

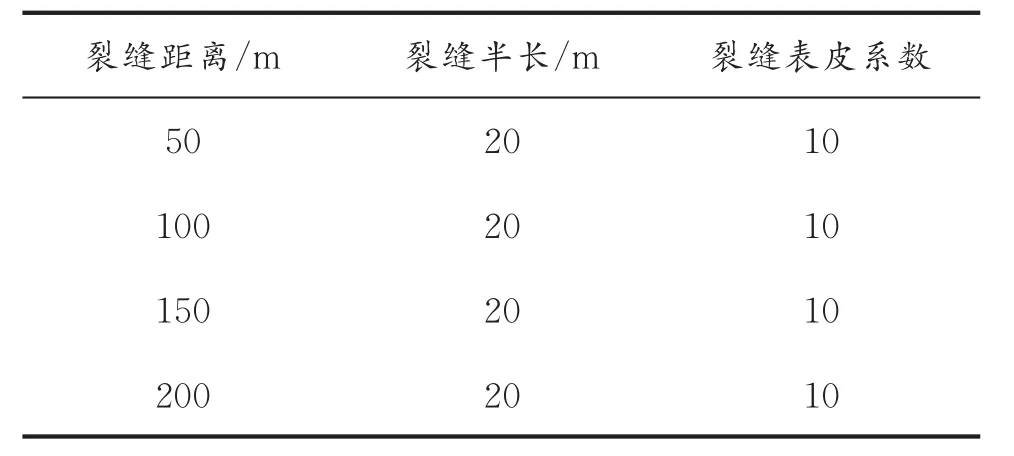
表1 裂缝参数Table1 Fracture parameters

基于上述原理，将耿文爽等[16]研制的多级压裂水平井试井解释软件转入产能评价模块，该模块包括基本参数、裂缝参数输入和计算模块三部分。输入参数后，绘制出对应的IPR曲线或产量递减曲线，如图3所示。

在表1方案的基础上，采用单因素变量法研究裂缝变长对压裂水平井产能的影响，如图4所示。裂缝间距不变，仍为50 m，设计方案如表2所示。

在其它参数不变的情况下，将图4与图3进行对比，结果表明，随着裂缝半长增加，压裂水平井产能增加，随着压裂水平井的生产，当压力下降到同一最低点时，由图3（a）可知，生产10 h产量为1.73×105m3/d；由图 4（a）可知，同一压力条件下生产10 h产量为1.87×105m3/d，但是由于裂缝长时成本较高，因此需根据实际情况优选最佳的裂缝长度。

图4 不同裂缝变长条件下不同生产阶段IPR曲线和产量递减趋势曲线Fig.4 IPR cur ve and pr oduction decline tr end cur ve of different pr oduction stages under differ ent cr acks conditions

表2 不同裂缝半长条件下的裂缝参数Table2 Fracture parameters under diffent fracture halflength conditons

在表1方案的基础上，采用单因素变量法研究裂缝表皮系数对压裂水平井产能的影响，如图5所示。其中，裂缝间距不变，仍为50 m，设计方案如表3所示。

通过上述对比方法可知，在其它参数不变的情况下，在生产能力相同时，随着裂缝表皮系数的增大，压裂水平井压降和产能均变化不明显，这是由于裂缝附近储层渗透能力越差，裂缝表皮系数对压力波传播范围内储层平均渗透能力的影响减弱，导致产能变化不明显。

图5 不同裂缝表皮系数条件下不同生产阶段IPR曲线和产量递减趋势曲线Fig.5 IPR cur ve and pr oduction decline tr end cur ve of different production stages under different cr ack skin factor conditions

表3 不同裂缝表皮系数条件下的裂缝参数Table3 Fractur e par ameter s under diffent cr ack skin factor

3 结 论

（1）应用多级压裂水平井试井解释及产能评价软件，计算出不同生产阶段下产量随井底流压的变化曲线，以及不同井底流压下产量随生产时间的变化曲线，通过这种方法能够对水平井不同生产阶段进行产能预测评价。

（2）通过对比同一生产阶段的IPR曲线和产量递减曲线可知裂缝距离、裂缝半长、裂缝表皮系数对水平井产能的影响的大小，结果表明，裂缝半长对产能影响远大于裂缝距离和裂缝表皮系数对产能的影响。