Halbach阵列双转子永磁电机磁场分析与转矩计算

2018-10-25高起兴井立兵罗正豪

微特电机 2018年11期

高起兴，王冲，井立兵，罗正豪

(1.三峡大学，宜昌 443002;2.燕山大学电力电子节能与传动控制河北省重点实验室,秦皇岛 066004)

0 引言

内、外双转子永磁电机具有单输入电端口和两个独立机械输出口，具备结构小、效率高、寿命长等优点,常被用于风力发电，电动汽车，水下航行器等领域[1-5]。然而，永磁电机的自身特性决定了其气隙磁场并非理想的波形分布，永磁电机感应电势和输出转矩性能的优劣较大程度上取决于气隙磁密的分布[6-10]；而双转子永磁电机具有双气隙结构，其内部气隙磁通分布更复杂，转矩波动更严重，因此，双层气隙磁通密度波形的好坏对电机性能的影响更为明显[11]。

与传统径向充磁磁体相比，理想的Halbach磁体生成的气隙磁场正弦度较高，谐波分量较小;同时，Halbach磁体磁场可以增强一侧磁密，减弱另一侧磁密,提高了电机的运行效率，减小了漏磁,降低了铁耗[12-13],这个特点使其非常适用于双转子电机双层永磁体结构。本文在文献[14-15]基础上，将双转子永磁电机永磁体分块，并进行有序Halbach排列，进而用有限元法分析、计算该电机内、外侧气隙磁密及转矩脉动。结果表明，与径向充磁相比，Halbach阵列双转子永磁电机气隙磁密正弦度高，谐波分量小，转矩脉动大大降低。

1 Halbach阵列计算方法及磁场分布

Halbach阵列原理是将不同充磁方向的磁铁按照一定规律排列,使气隙磁场可以按照正弦分布,主要分为内磁场和外磁场。理想Halbach阵列的整个气隙磁场呈现正弦分布[16-17]。

Halbach磁体的充磁方向按下式变化[18]：

θm=(1±p)θ

(1)

式中：p是极对数；“+”表示磁极为内极式；“-”表示磁体为外极式；θ是磁化矢量和θ=0之间的夹角，如图1所示。因此在极坐标下磁矢量的分布可表示：

M=Mrer+Mθeθ

(2)

式中：Mr=Mcos(pθ),Mθ=±Msin(pθ)，M为磁化矢量。

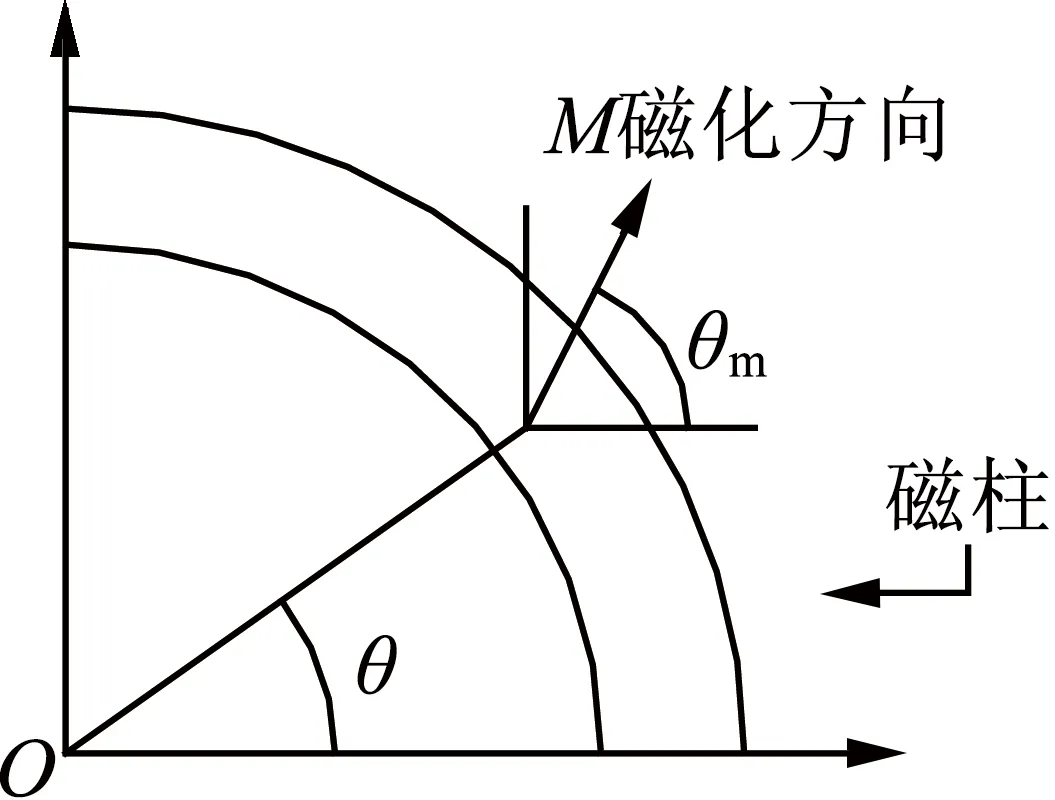
图1 θm和θ之间的关系

Halbach阵列磁体组成的内磁极电机气隙磁密表达式如下[19]：

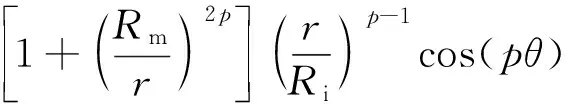
(3)

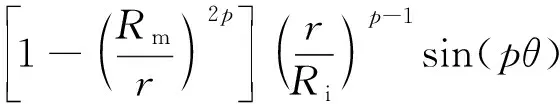
(4)

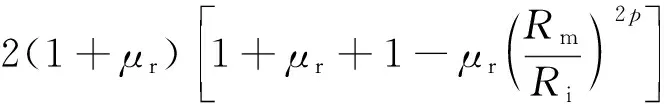
(5)

式中：μr为磁导率；Rm为转子铁心半径；Ri和Ro分别为Halbach阵列永磁体的内外半径。

Halbach阵列形成的磁场一侧磁通较密集，另一侧磁通较零散,显然磁自屏蔽特性使电机的运行更加高效[20]。图2是利用Ansoft计算的双转子永磁电机内、外转子永磁体每极4段Halbach阵列排列方式和产生的磁场示意图，内、外转子永磁体Halbach阵列排列方向相反，从而使内转子产生磁场外侧密集，内侧零散；外转子与其相反。

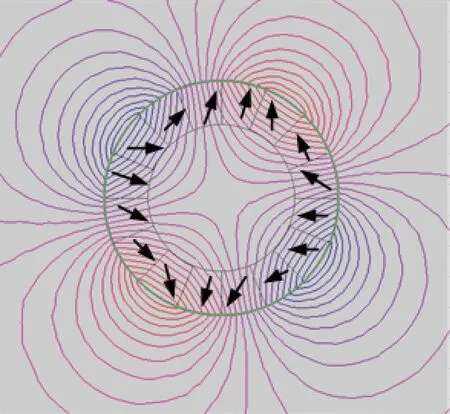
(a) 内转子磁场分布

(b) 外转子磁场分布

2 有限元分析

本文利用Maxwell软件对Halbach阵列永磁电机进行了有限元分析，电机参数如表1所列。

图3为该复合电机二维剖面图。可以看出，电机内转子与中间定子组成“内电机部分”，外转子与中间定子组成“外电机部分”，双转子电机由内、外电机复合而成，因此能够达到减小体积、降低质量和成本，加大输出转矩的效果。内、外转子同速异向旋转，并且，为了削弱由内、外转子永磁之间相互吸引和排斥的转矩，本文采用在定子铁心轭部中间引入厚度为2.5 mm的隔磁环[3]，如图4所示，由于隔磁环的存在，电机内、外部分磁路上相互独立，而在电路上相互耦合。

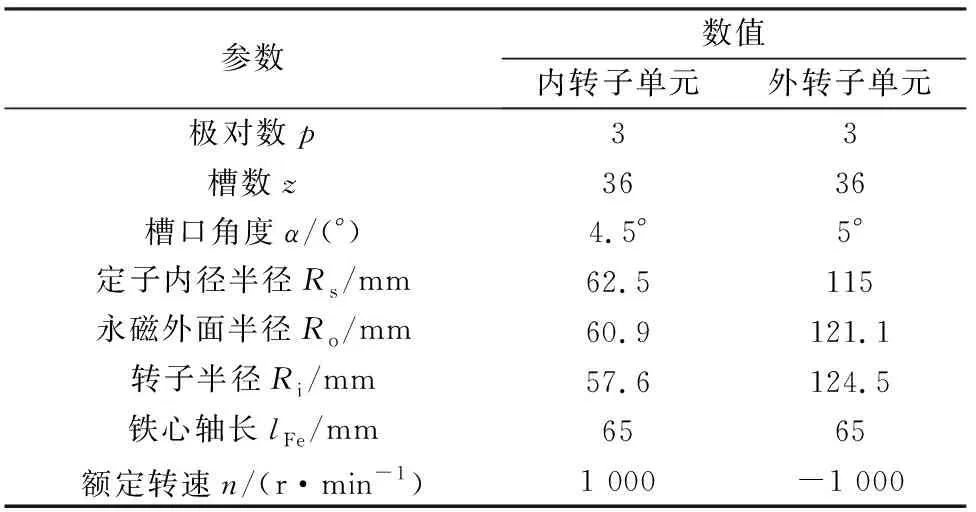
表1 电机模型参数

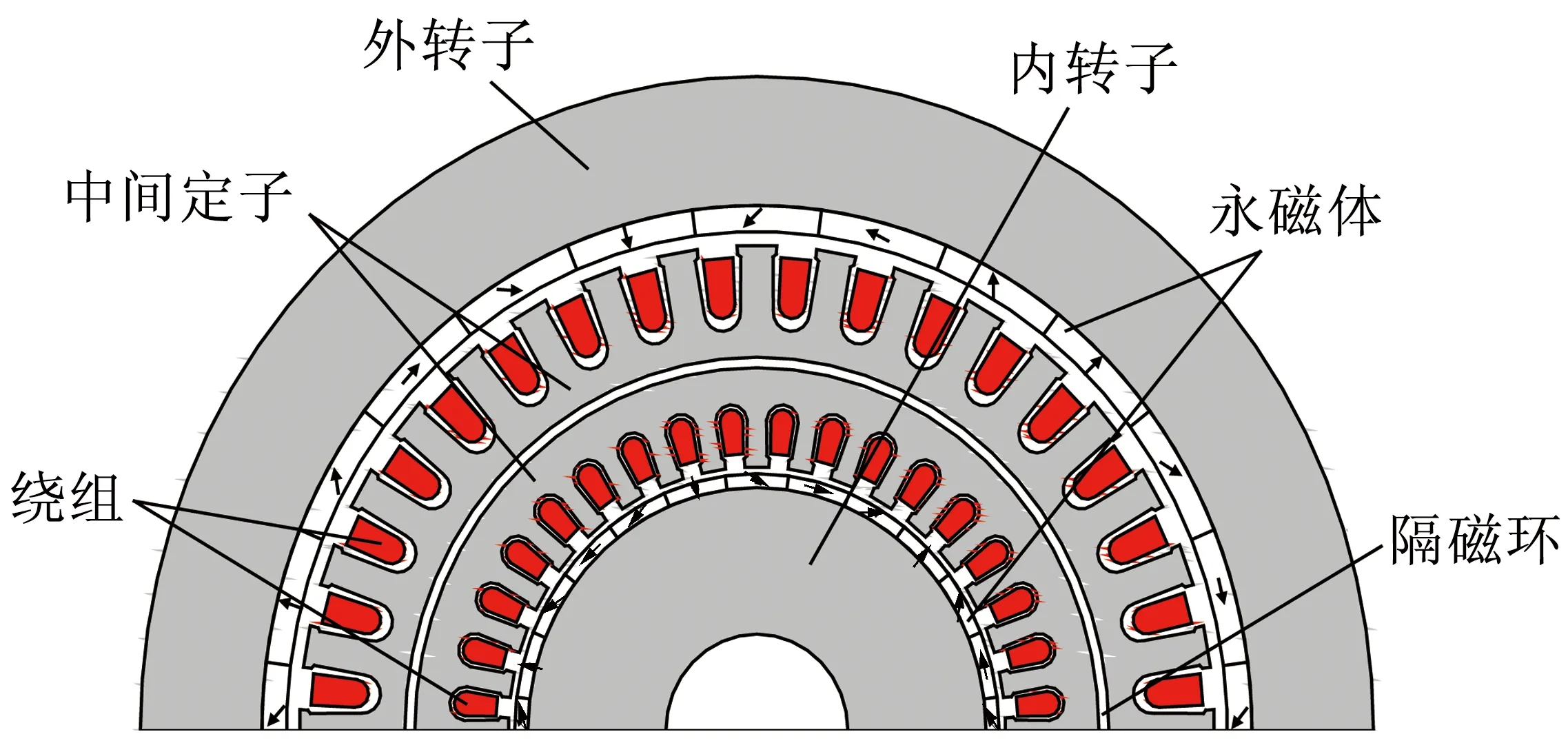
图3 电机剖面图

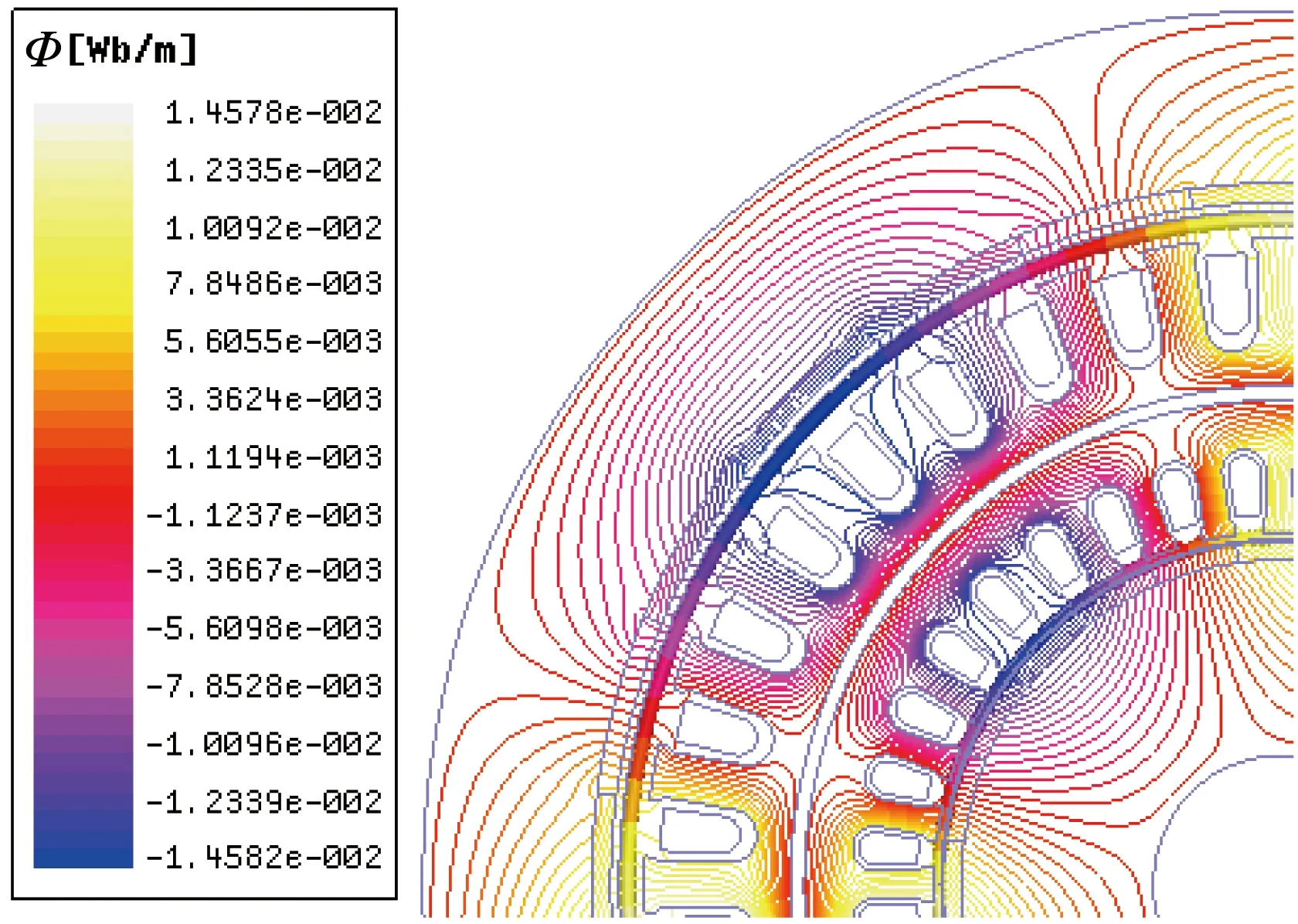
图4 磁力线分布

2.1 径向磁密比较分析

对于永磁电机，气隙磁通密度波形直接影响电机每极磁通量，进而影响电机的噪声和工作特性，所以，电机的气隙磁密波形正弦程度越高则效果越理想。本文对双转子永磁电机每极分4段，充磁角度如图3所示。将Halbach充磁与径向充磁电机的径向磁密波形进行比较，如图5所示。

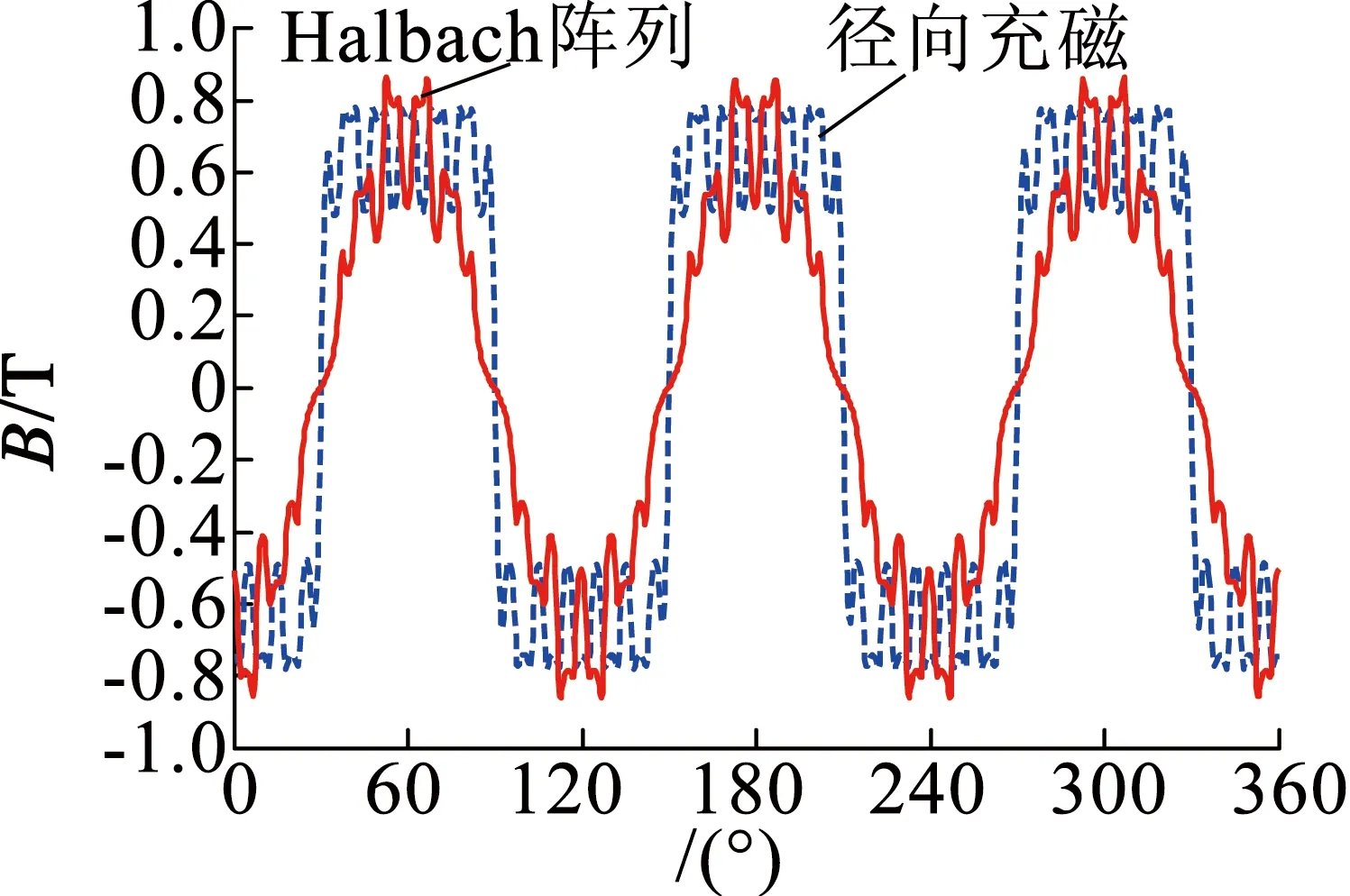
图5 内层径向气隙磁密波形图

对于电机内层径向气隙磁密，从图5可以看出，Halbach阵列产生的气隙磁密波形正弦程度明显更高。由表2算出， Halbach充磁谐波分量比例远小于径向充磁的谐波分量，THD值由40.79%优化到23.04%。

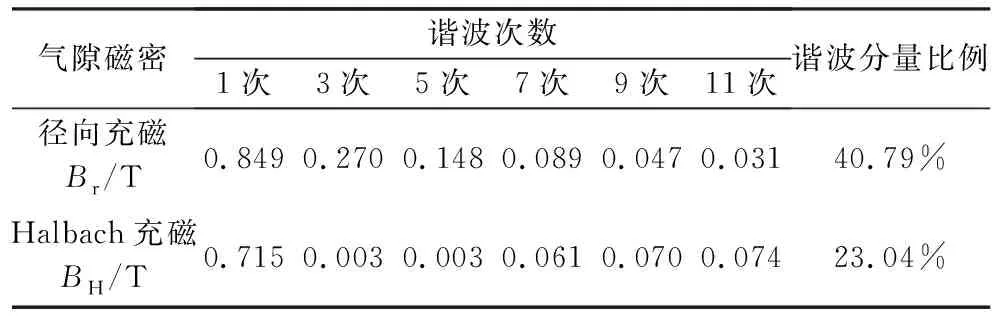
表2 内层气隙谐波分析

如图6所示，Halbach阵列的外层气隙磁密基波幅值更高，正弦程度更好。由表3得，对于双转子电机外侧径向磁密，Halbach充磁谐波分量远小于传统径向充磁，THD值由40.87%优化到25.19%。这表明，对于同尺寸的双转子永磁电机，每极4段 Halbach永磁阵列能大大提高电机的力能密度，减少损耗。

图6 外层径向气隙磁密波形

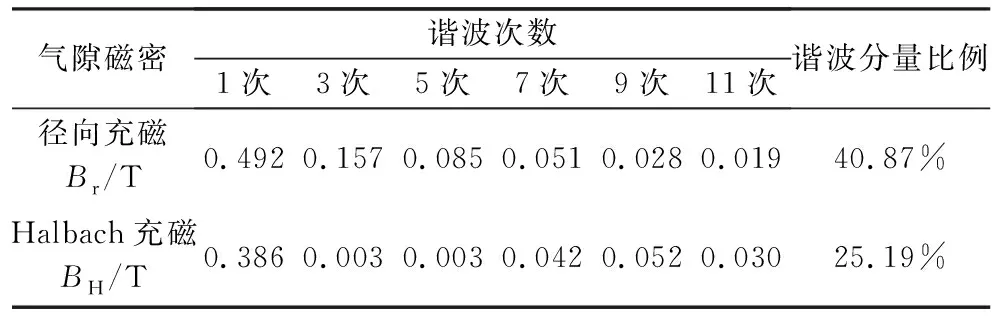
表2 外层气隙谐波分析

2.2 齿槽转矩比较分析

齿槽转矩存在于永磁电机中，会造成电机系统的振动和噪声，影响系统的控制精度，因此研究齿槽转矩的产生机理、削弱措施就显得尤为重要。永磁体和齿槽之间的吸引力产生了齿槽转矩，永磁电机齿槽转矩随齿和磁极的位置改变而呈周期性的变化。电机齿槽转矩公式如下：

(6)

式中：α为转子转角(电角度);W为气隙磁场的总能量;p为极对数。W可以表示：

(7)

为了验证Halbach阵列双转子永磁电机能有效减小齿槽转矩，本文以6极36槽双转子永磁电机为例进行分析。具体方法：保证电机内、外转子同速异向旋转，将电枢绕组电流设为零，以模拟绕组开路的情况，然后在其他条件不变的情况下，将永磁体的充磁方式由径向充磁改换为Halbach阵列充磁，最后将Ansoft有限元模型计算出来的两种充磁方式下的齿槽转矩进行比较。图7、图8是Halbach阵列和径向充磁齿槽转矩波形比较图。

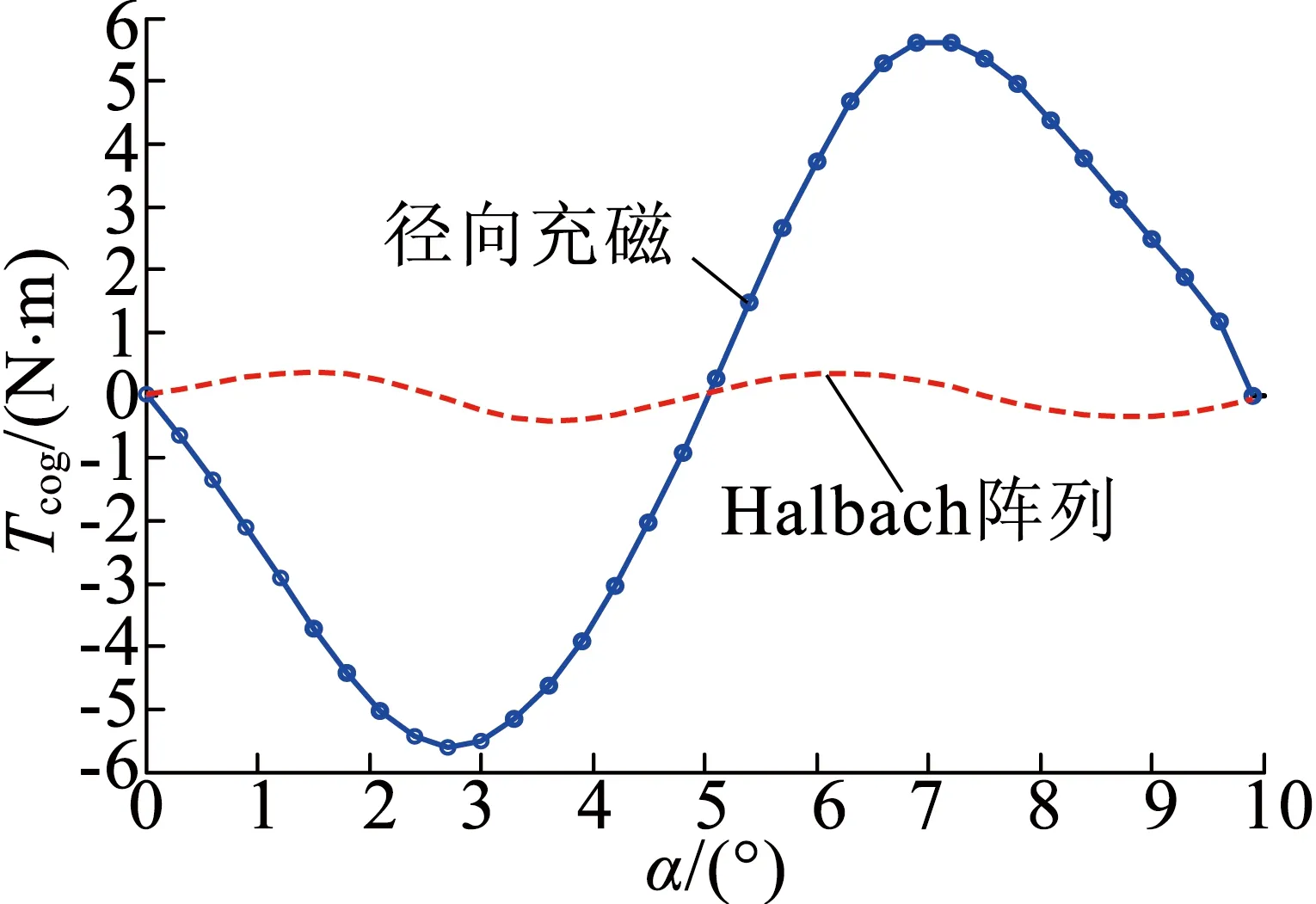
图7 内转子齿槽转矩

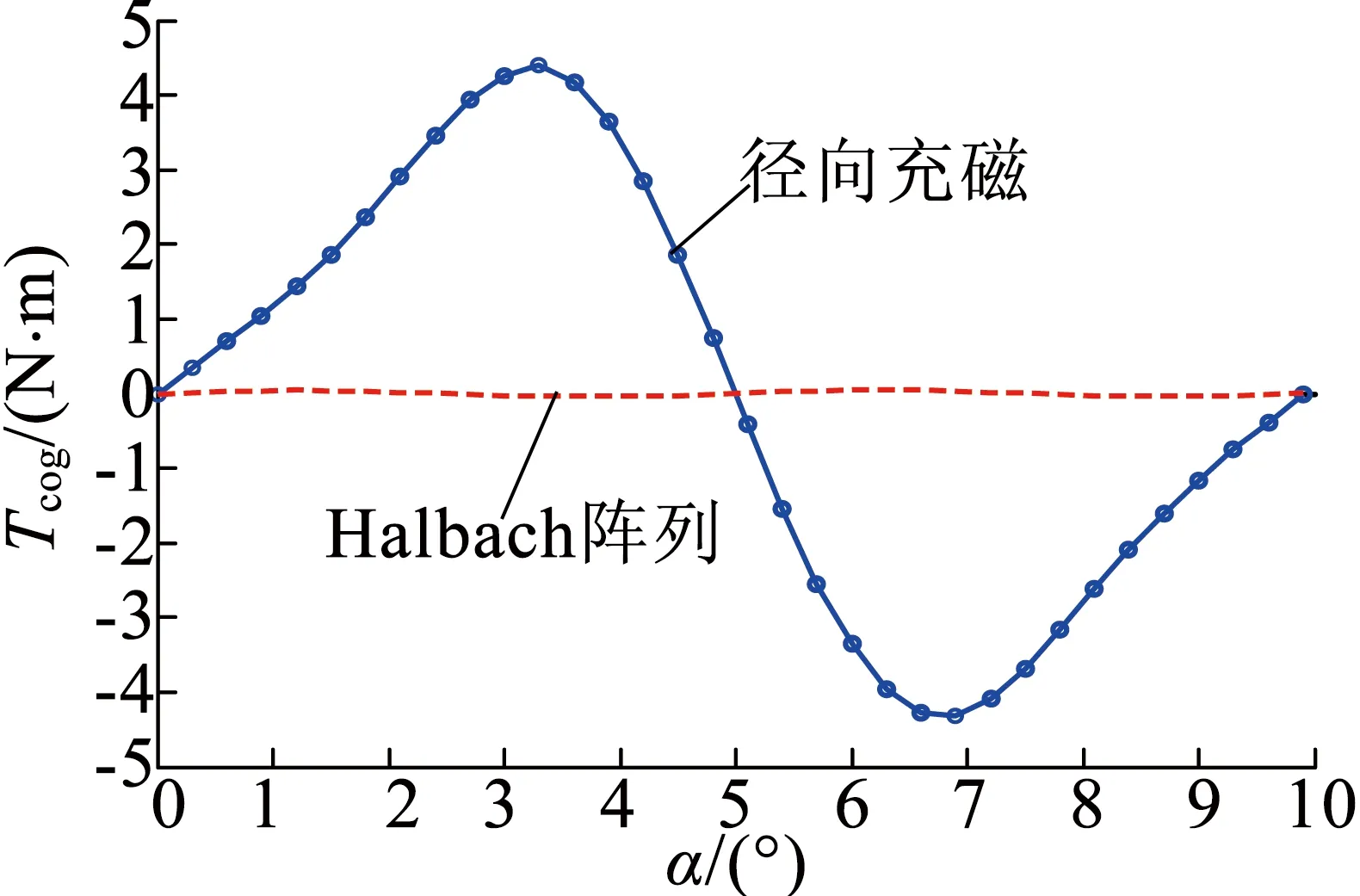
图8 外转子齿槽转矩

图7、图8显示，内转子电机中，径向充磁和Halbach阵列充磁的齿槽转矩分别为5.6 N·m和0.367 N·m;外转子电机中，径向充磁和Halbach阵列充磁的齿槽转矩分别为4.4 N·m和0.044 N·m。因此得出，无论对于双转子电机的内转子还是外转子，Halbach阵列方式充磁对齿槽转矩削弱效果都十分明显。

2.3 输出转矩脉动比较分析

本文以最大转矩平均值Tam和最小转矩波动kT作为优化目标。其中最大转矩平均值Tam是指在额定的电枢电流和功率角δ对应最大转矩/电流比的情况下一个电周期内的平均转矩，转矩波动系数kT定义如下:

(8)

在求解电机模型瞬态场输出转矩时，给三相绕组加载电流激励源，方程式如下：

(9)

电机内、外转子均同速异向运行，永磁体在径向充磁和Halbach阵列下的输出转矩对比如图9和图10所示。

通过计算得电机内转子永磁体在径向充磁情况下的转矩波动系数为36.46%，平均转矩为13 N·m；在Halbach阵列情况下内转子转矩波动系数为6.87%，平均转矩为11.93 N·m。电机外转子永磁体在径向充磁情况下的转矩波动系数为40.73%，平均转矩为-13.97 N·m；在Halbach阵列情况下外转子转矩波动系数为3.45%，平均转矩为-12.73 N·m。由计算结果可看出，与原始模型相比，优化后的电机内、外转子转矩脉动明显降低，电机运行稳定性大大提升。