基于弹性供应链的节点替代策略研究*

闫 妍， 吕 珊

(沈阳工业大学 管理学院， 沈阳 110870)

近些年，各种自然灾害和人为事件的发生使得生产企业的供应链时常发生中断[1]。美国“911”事件发生之后，所有到达美国的航运、空运全部暂停，很多生产企业的原材料供应全部中断；台湾“921”地震之后，台积电、联电等生产电子芯片和核心电子元件的生产企业关闭，给全球IT业造成了巨大的连锁影响，苹果公司不得不推迟新品发售，经济损失难以估计[2]；日本海啸发生后，东南沿海一带的半导体生产企业全部停工，由于日本芯片产品占全球芯片市场的五分之一，导致了全球范围内电子产品的闪存芯片供应短缺且价格大幅上涨。除此之外，飞利浦公司的大火、中国的SARS也给生产制造业带来了一系列的连锁反应和经济损失，供应链的中断问题和弹性应急策略成为了学术界近年来关注的热点问题[3-4]。

一、文献综述

供应链中断的时有发生使广大学者转向供应链修复问题的研究[5]。修复可以提高供应链的鲁棒性、柔性、抗扰动性和弹性[6]。其中，供应链的弹性是将力学中的弹性概念引入到供应链管理当中去，它是供应链的动态演化能力，是指“供应链受到突发事件的冲击之后，快速地恢复到原来功能的能力[7-8]。”弹性大的供应链具有抗干扰性强、受到打击之后恢复快的特点，是我们构建和修复供应链的目标。关于供应链的弹性国内外学者已经进行了一些研究，分别集中在供应链的弹性演化机理、供应链的弹性评估、供应链的弹性优化和供应链的弹性控制四个方面[9-10]。在供应链的弹性控制方面：杨锋等从汶川地震的道路选址能力入手，运用多目标决策方法寻求救援能力和应急成本之间的平衡[11]。许波桅等构建了运作成本模型，通过合理设置系统参数来获得弹性和成本的平衡[12]。Aviral等考虑了风险容忍度、各种生产成本，构建了混合整数规划模型，为平衡供应链效率和鲁棒性两个方面给出了应急方案[13]。吴中和等设计了供应链协调机制，考虑了信息不对称情况下的偏差成本，指出当突发事件发生时，通过调整最优订货量和批发价格来实现新的协调[14]。

在前人研究的基础之上，笔者在供应链弹性控制的范围内，提出了针对突发事件恢复供应链能力的节点替代新策略。该策略通过启用备用节点、替换供应链中的瘫痪节点，在新供应链网络中计算运输成本、启动成本、惩罚成本等，构建混合整数规划模型，计算出启用不同数量节点对应的最小成本并提出物流调度方案，在客户需求被满足时寻求弹性和成本的平衡。

二、模型构建

1. 问题描述

图1是一个五层的供应链网络，分别是a、b、c、d、e层。a为供应商层，含有A个供应商；b层为初级制造商层，含有B个制造商；c层为高级制造商层，含有C个制造商；d层为分销商层，含有D个分销商；e层是零售商层，含有E个零售商，零售商直接面向消费者。原材料从a层供应商开始输入整个网络，经过各层级的制造、加工，满足消费者的需求。在图1中，矩形表示网络中的节点，即企业；节点之间的连线表示企业之间存在物流输送，各节点的生产处理能力有最高限制。在网络运行过程中，由于存在自然灾害和人为灾难的可能性，网络中的某个节点可能突然中断生产。这时，中断的企业将生产任务迅速转移到远距离甚至海外的分厂或同类型的企业进行代加工，以便快速地满足市场需求，为企业重建争取时间。本文采用的应急策略便是在企业中断时快速选择替代生产企业，考虑生产能力、运输距离等综合因素，在成本限制的条件下，尽可能满足社会对该种商品的需求，维持该行业的物价稳定和供给需求均衡，给出应急的优化配置方案，为供应链的弹性应急管理提供数学依据。

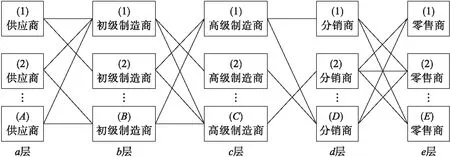
图1 供应链网络结构

2. 模型建立

(1) 模型假设。假设图1是一个5层的制造型供应链网络，每层分别含有A、B、C、D、E个节点。在该供应链网络中，每一层的节点功能相同，分别是供应原材料、制造、分销、零售等。原材料从供应商处进入网络，依次到达每一层，完成该层的功能，不允许跨层级跳跃。由于地震、洪水等不可抗力因素的影响，b层第二个节点企业生产中断。为满足用户需求，该企业需要从同类型企业X、Y、Z中选择一个或多个进行替代生产。

(2) 参数确定。cb为b层制造商的单位生产成本，cc为c层制造商的单位生产成本，cX、cY、cZ分别为企业X、Y、Z的单位生产成本；Labij为a层第i个供应商到b层第j个制造商之间的距离，Lbcij为b层第i个供应商到c层第j个制造商之间的距离，Lcdij为c层第i个供应商到d层第j个制造商之间的距离，Ldeij为d层第i个供应商到e层第j个制造商之间的距离；LXci为X企业c层第i个制造商之间的距离，LYci为Y企业c层第i个制造商之间的距离，LZci为Z企业c层第i个制造商之间的距离；p为各企业单位运输成本；lai、lbi、lci、ldi、lei分别为a、b、c、d、e层节点最大能力约束；Kbi为b层第i个制造商的缺货单位惩罚成本；m为用户需求。

(3) 决策变量确定。Qabij为a层第i个制造商到b层第j个制造商之间的物流量，Qbcij为b层第i个制造商到c层第j个制造商之间的物流量，Qcdij为c层第i个制造商到d层第j个制造商之间的物流量，Qdeij为d层第i个制造商到e层第j个制造商之间的物流量；QXci为X企业到c层第i个制造商之间的物流量；QYci为Y企业到c层第i个制造商之间的物流量，QZci为Z企业到c层第i个制造商之间的物流量。WXci、WYci、WZci分别为X、Y、Z企业和c层第i个制造商之间是否存在物流量，是取值为1，否取值为0。

(4) 目标函数和约束情况。考虑到制造型企业中成本的重要性，笔者提供了以供应链总成本为目标的替代节点选择及运行方案。供应链的总成本由三部分组成：生产成本、运输成本和缺货惩罚成本，目标函数对三项成本之和求最小值。其中生产成本为b、c层制造商及X、Y、Z企业的生产成本之和，表示为

(1)

运输成本是原网络中各路径运输成本与新增节点路径运输成本之和，表示为

(2)

缺货惩罚成本为b层第二个节点向c层所有节点供货量的惩罚成本总和，表示为

(3)

所以总成本的目标函数为

(4)

约束条件为：

① 物流平衡约束。供应链各层之间的物流量总和需要达到平衡，即

b层物流平衡约束为

(5)

c层物流平衡约束为

(6)

d层物流平衡约束为

(7)

③ 非零约束。供应链各节点之间显然要满足非零约束Qabij、Qbcij、Qcdij、Qdeij≥0；QXci、QYci、QZci≥0。

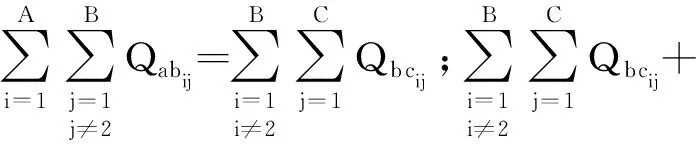
三、计算结果

为求解上述混合整数规划问题，使用WebSphere ILOG CPLEX12.7.1进行求解。CPLEX软件能提供灵活的高性能优化程序，解决线性规划、二次方程规划、二次方程约束规划和混合整型规划问题。运行计算机配置为：CPU i7-8550U，内存8 G，硬盘256 G固态。

以上程序均已对大量例子进行反复测算，计算结果均为满意结果，由于篇幅受限，本文给出小规模算例。

在图1所示的网络中，为计算简便，假设每层各有3个节点，网络共有15个节点。该网络生产的产品，消费者的总需求是8 000 t，各企业的生产成本、最高处理能力、单位生产成本和运输距离等数据已知，详见表1～3所示。

表1 各企业初始能力相关数据

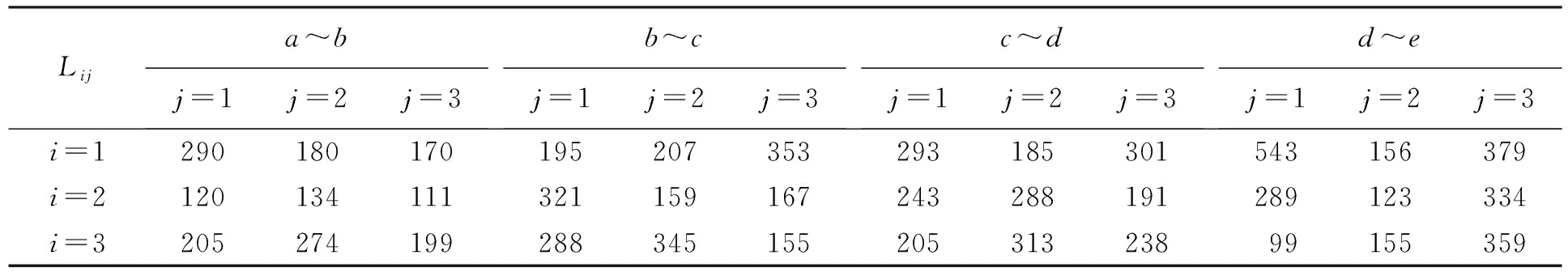
表2 各节点之间的距离 km

表3 各替代节点初始能力数据

本算例使用CPLEX12.7.1对规划模型进行求解，计算结果详见表4、5。该应急方案的最小成本为79 526 843元，各节点之间的最优物流量详见表4，其中0表示两节点之间无物流运输。在替代节点的选择上，该方案在Y企业中选择了节点1和节点2(即i=1和i=2)，在Z企业中选择了节点2，其他节点没有选择。替代节点与功能相同的原网络节点的物流量见表5，该应急方案满足了消费者需求，提高了供应链中断的弹性应急能力，最大程度地降低了节点中断带来的损失。

表4 网络应急调度方案(目标函数值为79 526 843元) t

表5 替代节点选择方案 t

四、结 语

从弹性角度对供应链进行优化和控制是供应链危机管理中的新视角，其强调供应链的迅速恢复，满足消费需求，维持市场稳定。本文基于供应链弹性，提出了应对供应链节点意外中断的替代节点选择方案，通过寻找同类型同功能节点替换中断节点，以求快速恢复供应网络的功能和运行。该方案给出了最小成本情况下资源的最优配置方案，提供了替代节点的合理选择，提出了新网络的应急物流调度方案，使消费者需求得到了快速的满足，最大程度地弥补了节点中断带来的损失，给供应链应急管理提供了一条新途径。