基于GARCH模型的我国创业板市场风险度量*
2018-10-25宋永辉
宋永辉, 陈 晨
(沈阳工业大学 经济学院, 沈阳 110870)
对于一个国家的资本市场来说,创业板市场无疑是不可缺少的重要部分,其主要意义在于为成长中的中小企业提供融资渠道和退出机制。国际上成熟的创业板市场已经比较完善,具有丰富的操作经验,而我国的创业板市场还存在一些缺陷与不足。无论对于创业板本身或暴露于创业板的主体而言,对风险的认识都是必不可少的。
一、文献综述

Neil(2016)的研究采用极值理论的方法估计GARCH模型的残差,度量了存在异方差特性的金融时间序列的尾部风险[7]。Ramazan(2015)对极值理论、GARCH族、历史模拟法等方法进行了比较分析[8]。Samit和Prateek(2017)利用条件极值理论(EVT)构建GARCH模型,并且进行了动态的预测能力模型与独立的GARCH模型的比较[9]。
二、我国创业板市场现状
我国的创业板市场成立于2009年10月,自成立以来,在不断暴露出问题的同时也不断地发展与完善。截至2017年7月12日,创业板市场从2009年的28家上市公司扩展到656家上市公司。2009—2017年中国创业板市场基本数据如表1所示。
由表1可以看出,2009年12月—2017年7月,我国创业板的上市公司数量、总发行股本(百万股)、总流通股本(百万股)都在不断地增长。创业板上市公司市价总值已经从2009年创业板刚成立时的1 610亿元连续增加到约49 780亿元,可见其规模不断扩大。但是在规模不断扩大的同时,其各个指标的增速并不一致。2009—2017年总发行股本和总流通股本一直保持着匀速稳定增长的状态,而市价总值和流通市值则在2009—2015年保持增长,但在2015—2017年有下降的趋势。
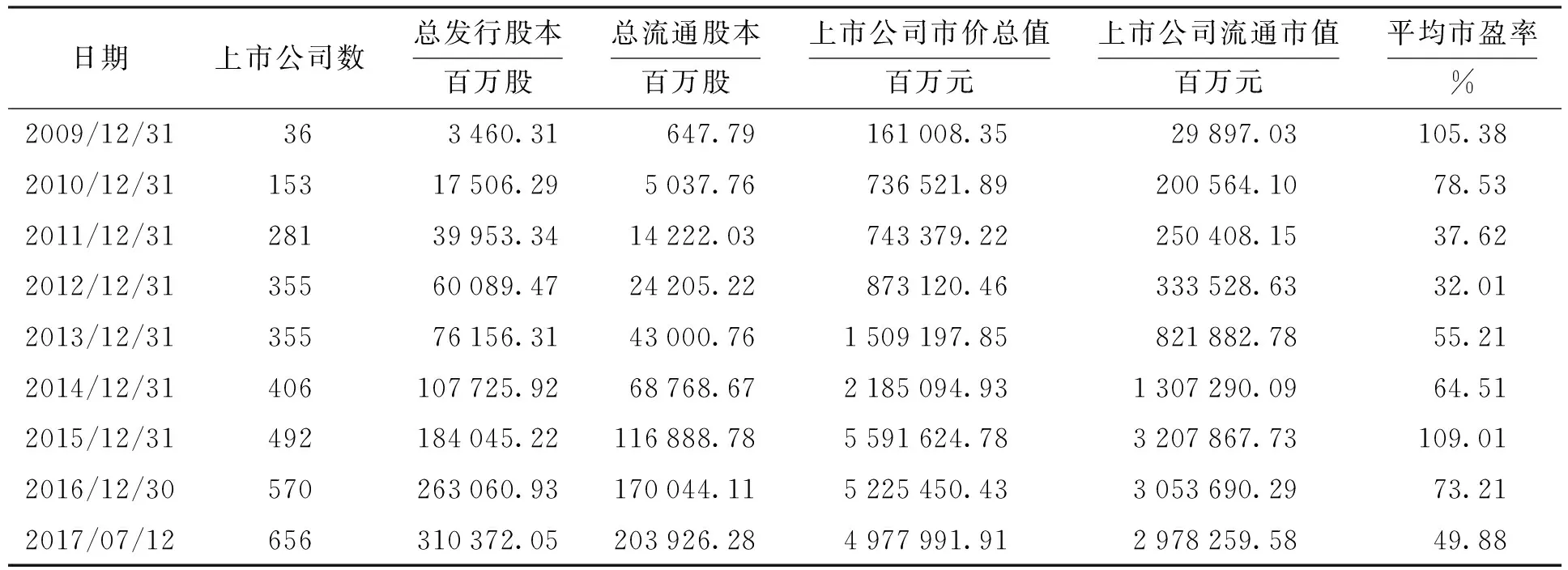
表1 2009—2017年中国创业板市场基本数据
创业板的增长态势值得鼓励,但在市盈率走高的背后却是高估值与高业绩增长水平的背离。在创业板市场,投资者们在高收益的引导下脱离基本的理论知识与分析,意识不到高风险的存在,盲目地抱着投机的心态一心想牟取暴利。因此,投资者对创业板市场进行冷静理性的分析、识别投资的利弊、保持冷静与谨慎是非常有必要的[10]。
三、GARCH-VAR模型
1. GARCH模型
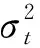
一般的GARCH模型可以表示为
(1)
(2)
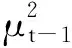
与波动的聚集效应相同:伴随着较大的波动后可能是更大的波动,较小的波动后伴随着更小的波动。Garch(p,q)模型是ARCH模型的扩展,因此都具备这一特点[12]。GARCH模型在描述高阶且计算量不大时优于ARCH模型,因而具有比ARCH更强的适用性。
2. VAR模型
1993年7月G30集团在一个报告中提到用“风险价值系统”来评估金融风险,这份报告是在研究金融衍生工具的基础上提出的。之后Morgan推算出了计算VAR的风险模型用以衡量风险[13]。2004年发布的新巴塞尔协议中进一步主张用VAR模型对商业银行面临的风险进行综合管理[14]。目前,国际金融机构已经广泛采用VAR作为衡量金融法风险的指标。
VAR的基本定义:在正常的市场条件下和给定的持有期内,某一金融资产或证券组合在未来特定一段持有期内的最大可能损失[15]。统计学公式表示为
Prob(ΔPΔt≤VAR)=θ
(3)
式中:ΔP为金融资产在持有期Δt的价值损失额;VAR为给定置信水平θ下的在险价值,即可能的损失上限;θ为给定的置信水平。在确定持有期和置信水平的情况下可以计算出资产或资产组合最大可能的预期损失,也就是VAR值。
四、实证分析
1. 数据的选取
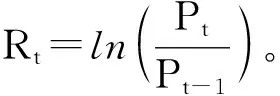
2. 数据的基本分析
(1) 数据的统计特征。数据的基本统计特征如表2所示。由表2可知,创业板综合指数日对数收益率均值为0.001 078,偏度为-0.740 38,左偏,峰度为5.134 497。数据在服从正态分布时,通常偏度为0,峰度为3,因此可以看出创业板综指日对数收益率有显著的尖峰厚尾特征,不服从正态分布。

表2 数据的基本统计特征
(2) 单位根检验。遵循AIC和SC最小原则,对创业板日对数收益率进行ADF单位根检验,结果如表3所示。由表3可知,ADF检验值为-30.210 53,P值为0.000 0,小于5%显著性的临界值,故拒绝序列不平稳的原假设,创业板综指的日对数收益率序列是平稳的序列。

表3 ADF检验结果
(3) 自相关检验。对创业板综合指数进行自相关检验,结果如表4所示。通过Eviews系统分析总结出创业板综合指数36阶滞后的AC值和PAC值。P值接近零,高阶后等于零,可见数据之间不存在明显的自相关性,也就是说创业板日对数收益率之间基本不存在自相关。
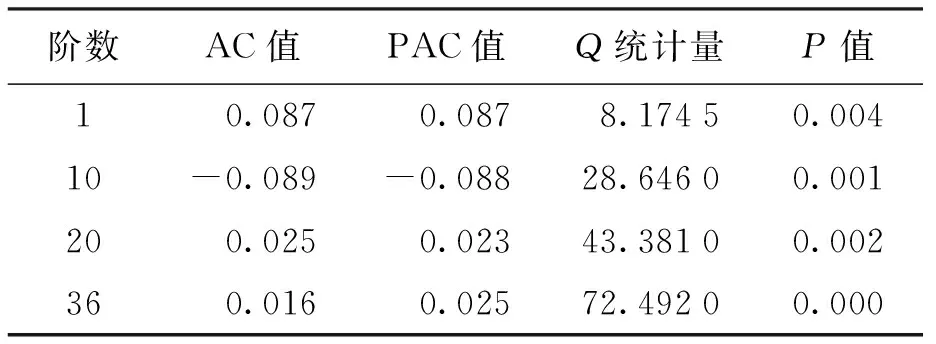
表4 自相关检验结果
(4) 正态分布检验。Q-Q图是最常用的视觉检测是否服从正态分布的常规方法,在数据满足正态分布时,它的Q-Q散点图会是一条直线。根据自相关检验结果绘制数据的Q-Q散点图,得出Q-Q散点图两边有凸起,中间弯曲凹陷,因此明显看出创业板综指日对数收益率是不服从正态分布的。
(5) LM异方差检验。创业板综指日对数收益率的波动集中在(-0.08,0.08),但在这个区间内价格波动较大,时高时低,有时激烈波动,有时平缓,可以看出其更容易在较大的波动后出现更大的波动,较小的波动幅度后随之而来的是更小的波动幅度,因此创业板综指日对数收益率存在显著的集聚性效应。
对创业板综指的残差平方进行自相关检验,自相关与偏相关系数AC和PAC显著不为零,Q统计量显著,因此拒绝不存在异方差的原假设,我国创业板市场综指的日对数收益率有明显的异方差性。
对数据进行ARCH效应检验,结果如表5所示。由表4可知,P值为零,也就是χ2分布的伴随概率P为0,创业板综指存在ARCH效应,拒绝不存在ARCH效应的原假设。
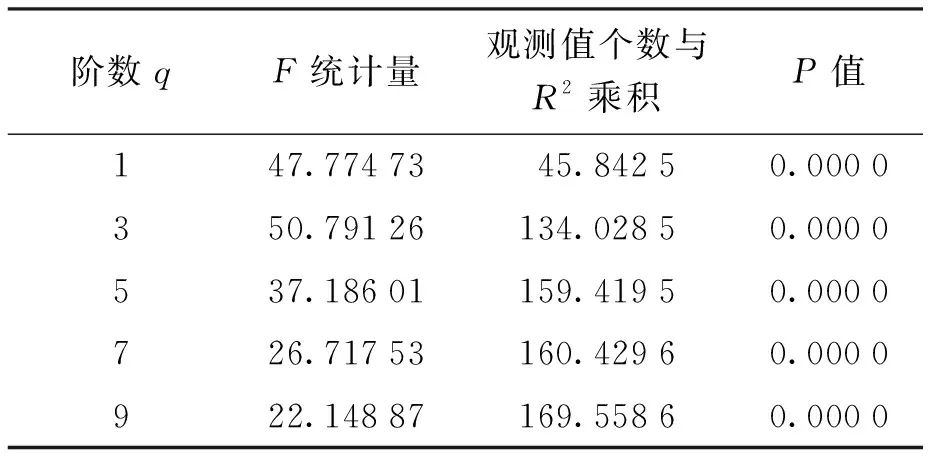
表5 ARCH效应检验结果
3. GARCH-VAR模型的建立
对数据进行ADF单位根检验、正态分布检验、自相关检验和异方差性检验后,可以判断出创业板综合指数日对数收益率是平稳的,在不满足正态分布的同时不存在自相关性,存在异方差并具有ARCH效应。因此,设收益方程为一般的均值回归方程,即rt=μ+σt,其中,μ为均值,σt为均值方程的残差。由于数列存在明显的异方差性,遵循AIC最小原则,经过反复的测试得出滞后阶数(p,q)为(1,1)时AIC值取到最小,所以本文模型均为GARCH(1,1)类模型。
(1) 基于正态分布的GARCH族模型参数及VAR检验值。每个模型对应两行内容,第一行为模型参数值,第二行为Z检验值(见表6)。由表6可知,模型参数在5%的显著性水平下都是显著的。因为常数项不影响效果的估计,故没有残留明显的异方差现象。这说明模型可以较好地拟合创业板综合指数日对数收益率的异方差现象。EGARCH模型的非对称项系数γ1=-0.004 779显著小于零,根据指数模型的对数性质,可以得出利空消息带给创业板市场的波动比等量的利好消息更大,创业板市场存在明显杠杆效应的结论。
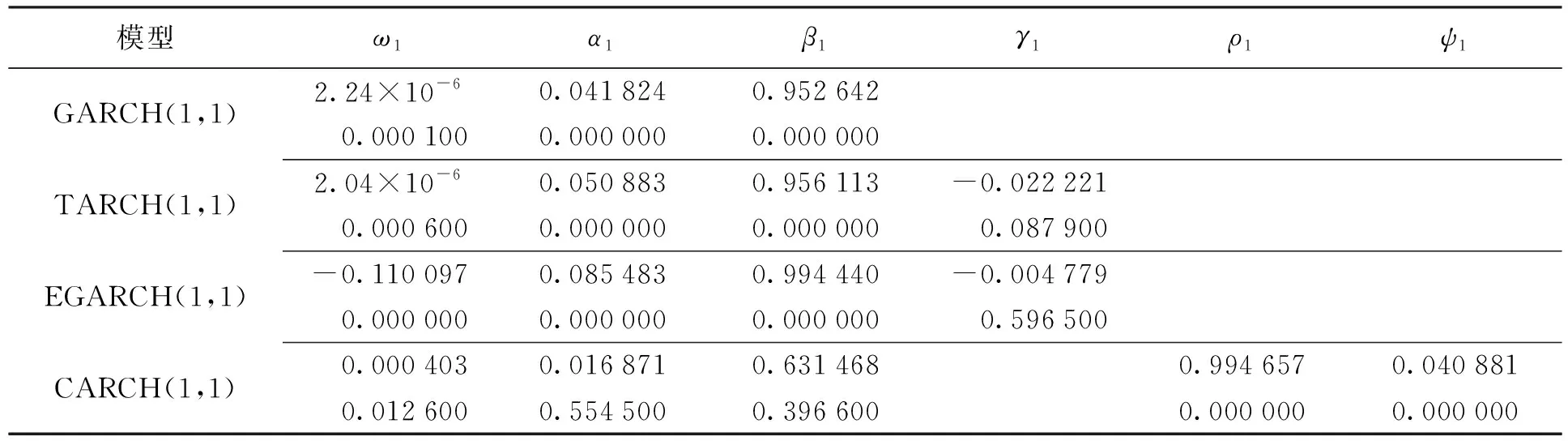
表6 基于正态分布的GARCH类模型参数值及Z值
注:ω为c值,α为RESID(-1)2值,β为GARCH(-1)值,γ为RESID(-1)2与RESID(-1)<0值的乘积,ρ为C(3)值,ψ为C(4)值,下同。
基于GARCH模型参数,计算得到VAR的统计特征值及Kupiec检验结果(见表7)。由表7可知,在95%和99%置信水平下,通过正态分布GARCH类模型得出的VAR均值差别不大,而最大值和最小值的差别却比较大。由表7可知,LR检验的结果:在显著水平为5%的情况下,TARCH(1,1)和CARCH(1,1)模型的LR检验值显著小于3.41,也就是TARCH(1,1)、CARCH(1,1)模型通过了LR检验,相对于没有通过检验的模型结果更加准确。在1%的显著水平下,GARCH(1,1)模型和EGARCH(1,1)模型LR检验的结果小于6.635,所以这两类模型都通过了检验,即GARCH(1,1)和EGARCH(1,1)模型下计算VAR检验值得到的结果较准确。
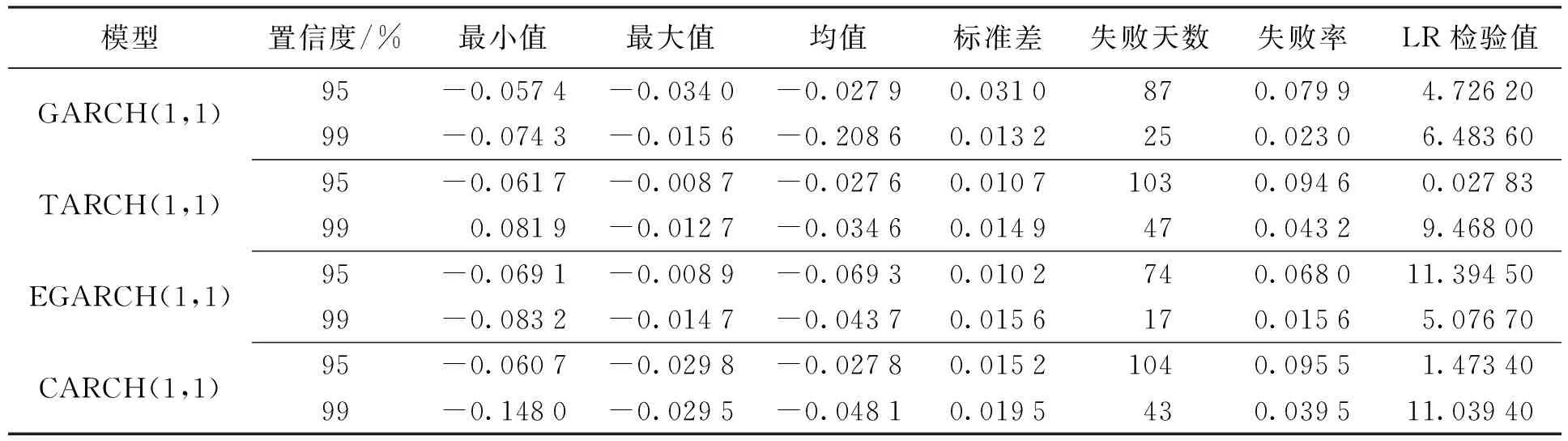
表7 基于正态分布的GARCH类模型VAR返回检验值
(2) 基于T分布的GARCH族模型参数及VAR检验值。模型参数在5%的显著性水平下结果均较为显著,检验残差的LM效果估计和残差检验异方差性见表8、9,结果表明没有残留明显的异方差现象,因此模型可以较好地拟合创业板综合指数日对数收益率的异方差现象,并且从参数估值结果可以看出创业板指数存在明显的非对称效应。
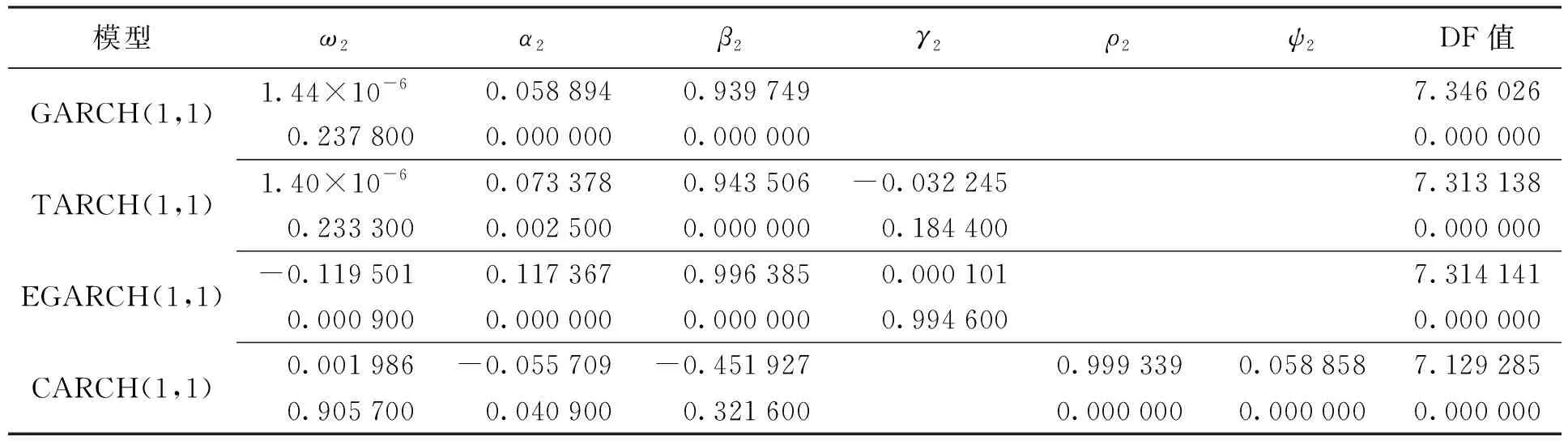
表8 基于T分布的GARCH类模型参数值及Z值
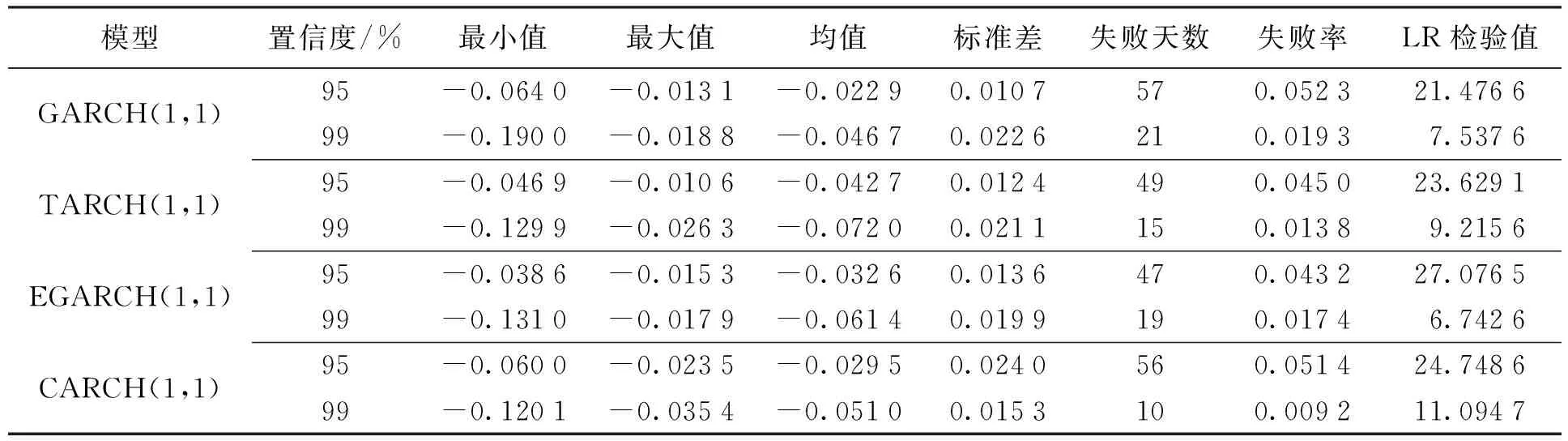
表9 基于T分布的GARCH类模型VAR返回检验值
由表9可知,在95%和99%置信水平下,各种计算出的VAR均值之间差距较最大值与最小值之间差距大。在5%的显著水平下GARCH(1,1)、EGARCH(1,1)、TARCH(1,1)、CARCH(1,1)模型的LR检验值均大于3.841;在1%的显著水平下,模型的LR检验值均大于6.635,所以,在显著性水平为1%和5%时都要拒绝原假设。可见,基于T分布的创业板综合指数计算出的VAR值过于保守,存在着风险被缩小的可能。综合而言,在T分布假设下,根据创业板综合指数日收益率各种GARCH类模型计算的参数值和Z检验结果,得出结论:创业板综合指数日收益率在服从T分布时是不合理的。
(3) 基于GED分布的GARCH族模型参数及VAR检验值。检验残差的LM效果估计和残差检验异方差性见表10、11,同样没有残留明显的异方差现象,因此模型可以较好地拟合创业板综合指数日对数收益率的异方差现象,创业板指数存在明显的非对称效应。GED分布下各模型估值结果的尾部参数即V值在1.45上下波动,因此,相较于其他分布,GED分布可以更好地刻画创业板指数日对数收益率数据的厚尾特征。
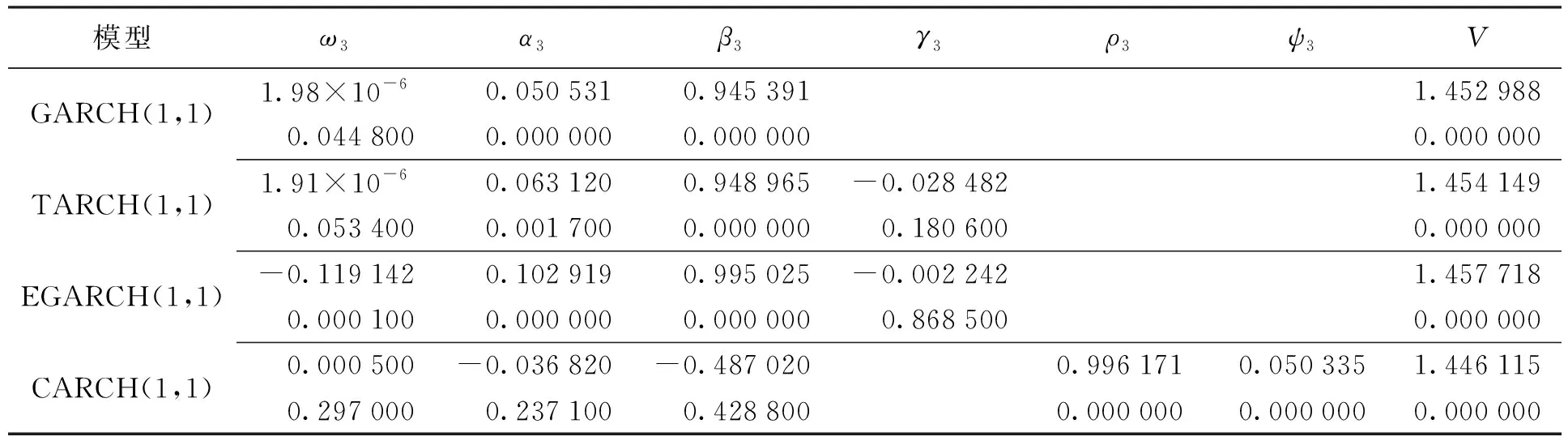
表10 基于GED分布的GARCH类模型参数值及Z值
注:V为GED PARAMETER值。
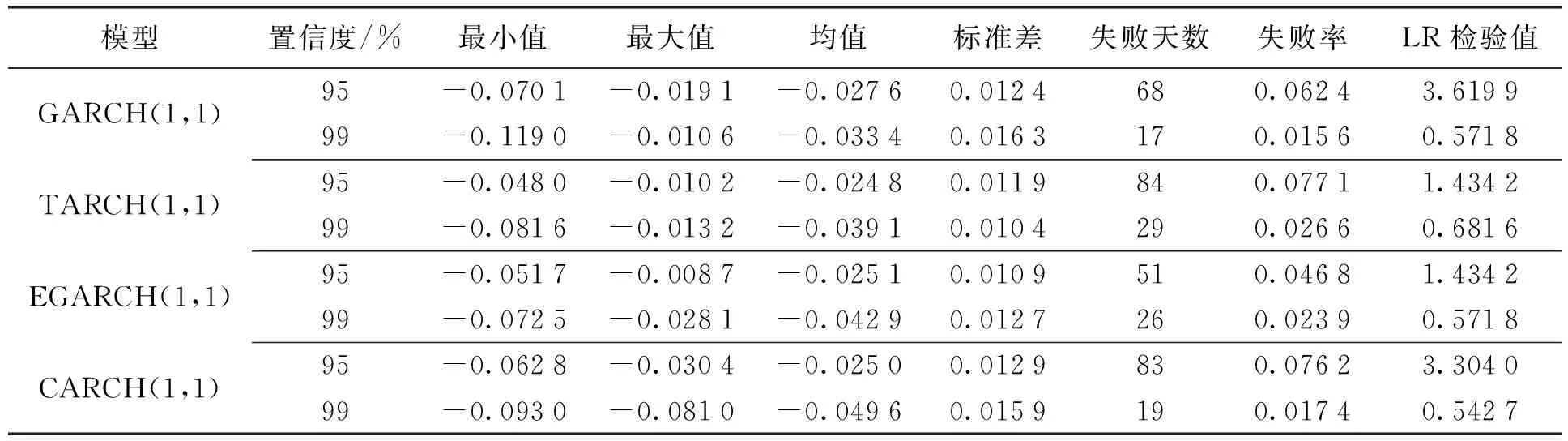
表11 基于GED分布的GARCH类模型VAR返回检验值
由表11可知,基于GED分布与基于正态分布假设的估计的结果比较相似,检验残差的LM效应,结果显示残差不再有显著的异方差现象,GED分布下的模型较好地拟合了数据的异方差现象。在5%的显著水平下,GARCH(1,1)模型、EGARCH(1,1)模型、TARCH(1,1)模型、CARCH(1,1)的LR检验值均小于3.841,可见4个模型全部通过了LR检验,意味着在GED分布下GARCH类模型得出的VAR值结果都比较精确。而在显著性为l%的情况下,LR检验值远小于6.635。所以,在两种置信水平下,GARCH(1,1)模型、EGARCH(1,1)模型、TARCH(1,1)模型、CARCH(1,1)模型都能够比较好地拟合创业板市场风险。
五、结 论
选取中国创业板市场综合指数,分别在正态分布、T分布、GED分布假设下,运用GARCH类模型计算VAR值并进行Kupiec检验,对创业板市场风险进行度量。对比分析不同显著性水平下的计算结果,得出以下结论:
第一,分析创业板块日收盘价对数收益率序列的统计特征,得出创业板综指日对数收益率有显著的尖峰厚尾特征,不服从正态分布,且其波动呈现出聚集性和持久性。
第二,正态分布下采用TARCH(1,1)模型和CARCH(1,1)模型计算VAR值时得到的结果较准确,而基于T分布的创业板综合指数计算出的VAR值过于保守,存在着风险被缩小的可能。只有GED分布在两种显著性水平下都能够很好地拟合数据,在GED分布下计算得出的VAR值的结果相对科学、精度高。四类GARCH模型计算得到的VAR值、失败率、失败天数、VAR标准差的差距都不大,从而可以看出模型种类并不是VAR值结果的决定性因素。
第三,创业板市场存在明显的杠杆效应即波动的非对称性,从模型参数可以看出利空消息带给创业板市场的波动比等量的利好消息更大,即负的冲击带来的波动大于正的冲击。
第四,在实际的投资决策过程中,投资者应选择适当的GARCH类模型才能更好地规避风险。投资者在创业板市场进行投资选择时,可以利用VAR进行风险评估和预测,根据理论基础选择投资观念,根据分析来实时更新投资策略。研究表明,VAR值随着置信水平的不同而有所不同,设定置信水平越高,风险价值VAR值也就越准确,也就意味着投资者可以在更准确地意识到风险的基础上有更大可能避免风险带来的损失。同时,创业板市场的杠杆效应也提醒投资者理性投资,不要盲目跟风。所以,投资者要根据实际情况为自己量身定制投资方案,及时更新投资方法和策略,灵活投资,这样才能保证风险和收益的最佳分配。
