基于QS算法的改进算法QS_I

李莉

（福州职业技术学院信息技术工程系，福州 350100）

0 引言

在当今大数据时代，数据信息量在迅速膨大，如何快速准确地找到特定的信息是大数据领域研究的重点。不管是生物信息领域、航海领域、金融领域、文学领域还是计算机领域，文本都是必不可少的信息组成元素，模式匹配算法不仅应用在模式识别领域，也广泛应用于文本挖掘、网络入侵检测系统（NIDS）等领域，所以寻找精确而有效的模式匹配算法已成为研究的焦点之一[1-2]。

本文研究的算法是基于字符比较的单模式匹配算法。BM（Boyer-Moore）算法[3]是经典的单模式匹配算法，基于BM算法的改进算法有BMH算法[4]、QS算法[5]、FQS算法[6]等，I_BMH2C算法[7]和QSP算法[8]是基于QS算法提出的两种改进算法。本文在QS算法基础上提出一种新的改进算法 QS_I（QS Improvement）算法，并将QS_I算法与QS算法、I_BMH2C算法和QSP算法的性能做了对比，理论与实验均证明QS_I算法的性能均高于 QS、I_BMH2C、QSP 算法。

1 相关算法分析

本文中的文本以T=T[0...n-1]表示，长度为n；模式串以P=P[0...m-1]表示，长度为m；且满足条件n>=m。按照单模式匹配算法的定义，找出文本T中所有匹配的模式串P的起始位置j:T[j]=P[0],T[j+1]=P[1]......T[j+m-1]=P[m-1]。

1.1 QS算法

Horspool在1980年提出改进与简化BM算法BMH算法[4]，1990年Sunday在BMH算法的基础上提出新的改进算法BMHS算法，简称QS算法[5]。QS算法的改进思路：预处理部分只引用坏字符跳跃规则进行匹配，在当前匹配窗口出现不匹配时，模式串必然右移，末字符的下一字符（T[j+m]）是下次匹配窗口的处理对象，使用字符T[j+m]决定模式串当前的右移量，若字符T[j+m]未在模式P中出现时，窗口右移量为m+1，大于BM算法的最大右移量m。QS算法预处理部分的坏字符规则略有改进，公式如下：

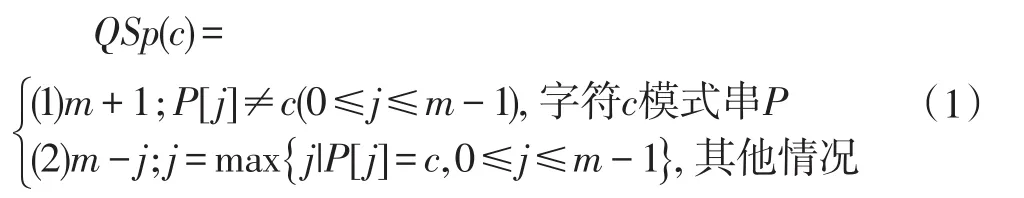
以文本串T=“DCBDADBCDBDCCADCCBADACDC”和模式串P=“CBADACDC”为例，匹配过程如表1所示。预处理后得到数组QBCp的值为：QBCp[A,B,C,D]=[4,7,1,2]。

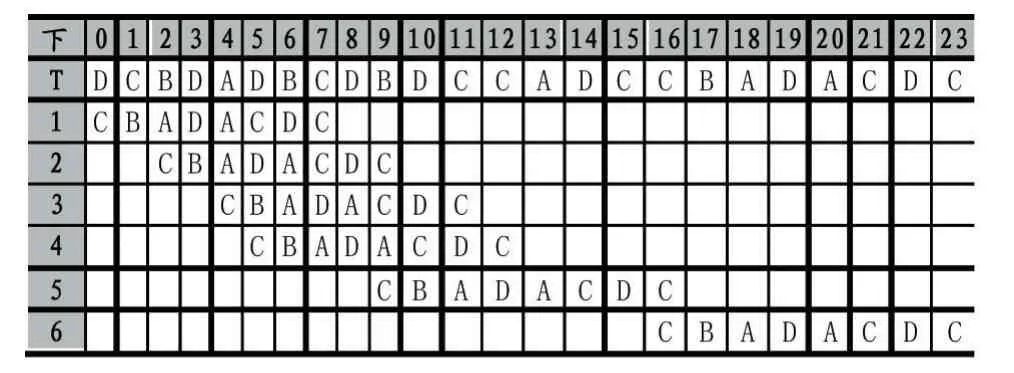
表1 QS匹配过程

1.2 I_BMH 2 C算法和QSP算法

2014年王艳霞在BMH2C算法[9]的基础上提出一种改进算法——I_BMH2C算法[7]，BMH2C算法使用末字符（T[j+m-1]）和下一字符（T[j+m]）两个字符作为子串来决定右移量，但BMH2C算法并没有考虑双字符在模式串中重复出现的情况。I_BMH2C算法的改进思路：分析双字符在模式串中出现0次、1次和1次以上三种情况，利用两个右移数组和一个模式串预处理数组，在匹配过程中通过判断字符T[k+2]与模式串预处理数组中相应字符是否相等，再选择右移数组之一的对应值作为当前窗口的右移量[9]。

2016年LI结合BMH2C算法和I_BMH2C算法的不足之处，提出一种改进算法——QSP算法[8]，QSP算法预处理部分只从单字符的角度进行考虑，找出模式串中出现1次以上的单字符，计算出这些字符的跳转期望值差，得到最大差值和相应字符P[maxPos]，并修改第二跳转数组的值；在匹配部分先比较P[maxPos]和T[j+maxPos]，再选择相应的跳转数组进行右移。

I_BMH2C算法分析T[j+m-1]和T[j+m]双子字符和T[k+2]字符，在预处理部分计算复杂度高，双字符在模式串中出现1次以上的情况比单字符重复出现的概率低，每次右移量并不能最大优化，QSP算法的运行效率明显高于I_BMH2C算法。QSP算法在匹配阶段，先只匹配P[maxPos]和T[j+maxPos]，不是与文本一一进行比较，在相等的情况下，ESi的值如果大于QS预处理规则的距离，窗口的右移量将得到提升，但QSP算法窗口最大右移量只为m+1，与QS算法的最大右移量一致，QSP算法的最坏时间复杂度为O(n*m),最好的时间复杂度为O(n/m)。综上所述，以上两种改进算法都有待进一步提升[10-11]。

2 QS_I算法

2.1 QS_I算法思路

QSP算法的运行效率比QS算法好，但QSP算法的最大右移量只为m+1，具有一定的局限性。本文结合QSP算法的不足之处，提出一种新的改进算法QS_I算法，QS_I算法是基于模式串单字符的QS改进算法，它的改进之处在于预处理考虑模式串中重复出现的单字符，计算出所有单字符距离前部分最近出现同样字符的距离，获取距离最远的单字符p[pfi]（下文用P_WORD表示）、此字符在模式串中的位置pfi值和模式串初步右移量SHIFT_1，在匹配阶段只用模式串的单字符P_WORD与相应的文本字符（T[j+pfi]）进行对比，两字符不匹配，预测模式串初步移动SHIFT_1距离后模式串和文本依旧不匹配，再根据跳转数组shift决定模式串第二次右移的距离为shift[s[j+SHIFT_1+m]，QS_I算法的最大右移量为m+1+SHIFT_1，大于QSP算法。

QS_I算法分为预处理阶段和匹配阶段两部分，QS_I算法的流程图如图1：

图1 QS_I算法流程图

2.2 预处理阶段

QS_I算法的预处理部分结合QS算法的预处理，并作相应的改进，预处理部分得到的是距离最远的单字符P_WORD的位置pfi值、模式串初步右移量SHIFT_1和shift数组。shift数组仍采用QS算法的预处理规则(公式1)，shift数组在QS_I算法中的作用是计算模式串末字符对应文本位置的下一个字符的跳转距离；QS_I算法预处理的改进部分体现在得到P_WORD值的过程中，整体分析模式串，计算出所有单字符距离前期最近出现同样字符的距离，比较得出最大的距离SHIFT_1值和单字符P_WORD的位置pfi值。预处理部分算法的时间复杂度为O(m*m)。

预处理过程的主要改进伪代码如下：

int ds=-1,SHIFT_1=0,flag=0;

int pfi=m-1;//默认是模式串的末字符

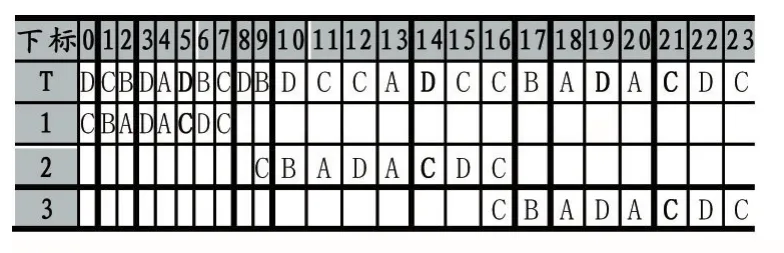
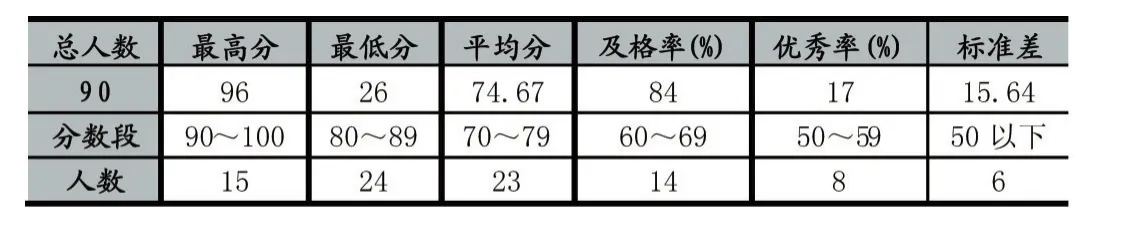
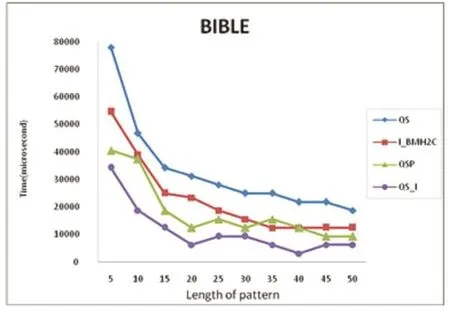
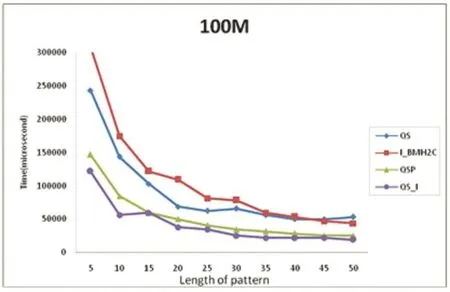
for(i=1;i

{

for(j=0;j

{

if(x[j]==x[i])//找最右边出现的同样字符

{

ds=i-j;//计算单字符距离前部分最近出现同样字符的距离

}

}

if(ds>=SHIFT_1)//比较得出最大的距离SHIFT_1值和单字符P_WORD的位置pfi值

{SHIFT_1=ds;

flag=1;

pfi=i;

}

ds=-1;//重置ds

}

同样以模式串P=“CBADACDC”为例,引用公式（1）计算得出shift数组的值为：shift[A,B,C,D]=[4,7,1,2]。引用上面的伪代码进行计算，得出相应的值为P_WORD=P[5]='C'，pfi=5,SHIFT_1=5-0=5,计算过程如表2所示：

表2 QS_I预处理过程

2.3 匹配阶段

QS_I算法的匹配阶段分为两个步骤，具体核心代码如下：

int SHIFT_1=preQs_IBc(p,m);//计算模式串初步的右移量

char PM_WORD=p[pfi];//模式串中间字符

while(j

{

//1.模式串的单字符P_WORD与相应的文本字符

（T[j+pfi]）不相等

while(T[j+pfi]!=P_WORD)

{

//指针j右移距离=初步的移动距离+再次的右移量

j=j+SHIFT_1+shift[T[j+SHIFT_1+m]];

if(j>n-m)

{

return

}

}

//2.两字符若相等，则引用QS算法匹配过程

compare P[0…,m-1]and T[j,…j+m-1]

if all matched then do

output j

end if

j=j+shift1[T[j+m]];//指针j的距离直接引用QS算法规则计算

}

匹配阶段的改进思路：先直接比较模式串单字符P_WORD与相对应的文本字符T[j+pfi]，若两字符不等，且字符P_WORD距离左边SHIFT_1的距离又重复出现，那么模式串移动SHIFT_1后，模式串显然不匹配当前对应的文本字符串，再引用shift数组，计算相对应的文本下一字符(T[j+SHIFT_1+m])的右移量SHIFT_2（shift[T[j+SHIFT_1+m]]），指针j跳转距离为SHIFT_1+SHIFT_2；单字符P_WORD没有在模式串前部分出现过，SHIFT_1=0，SHIFT_2=T[j+SHIFT_1+m]=T[j+m]，表示直接引用QS规则进行右移。若两字符相等，说明在当前指针j位置，存在全匹配的可能性，再进行一一比较。

在匹配过程中，QS_I算法的最坏搜索时间复杂度为O(m*n)，最好时间复杂度为O(m/n)[12]。

同样以文本串 T=“DCBDADBCDBDCCADCCBA⁃DACDC”和模式串P=“CBADACDC”为例，预处理后得到的值为 pfi=5，P_WORD='C'，SHIFT_1=5，数组 shift的值为：shift[A,B,C,D]=[4,7,1,2]。

匹配过程如表3所示。

表3 QS_I匹配过程

如表3所示，在第一次匹配窗口中，文本指针j=0,因为 P[5]≠T[0+5]即'D'!='C'，所以 j=j+SHIFT_1+shift[T[j+SHIFT_1+m]]=0+5+shift[T[13]]=5+4=9;在第二次匹配窗口中，P[5]≠T[9+5]，j=9+5+shift[9+5+8]=14+2=16；在第三次匹配窗口中，P[5]=T[16+5]，则进入搜索全匹配模式串阶段，并找到一个全匹配模式串P，输出当前指针j=16。

QSP算法的匹配过程如表4所示：

表4 QSP匹配过程

图2 bible文本运行时间图

从表1、表3、表4可以看出，QS算法、QSP算法和QS_I算法的匹配窗口次数分别是6次、5次和3次，QS_I算法的比较窗口次数明显低于QS算法和QSP算法的窗口次数。通过以下的实验证明QS_I算法的匹配效率确实高于QS算法和QSP算法。

3 实验结果

本文针对QS算法、I_BMH2C算法、QSP算法和QS_I算法进行对比实验分析。算法是在Visual C++6.0编译器上实现，并运行在CPU为Intel 2.30GHz，内存为4GB的计算机上，算法采用C语言实现。

本文实验的文本是bible.txt和100M128.txt，bible.txt文本来源于坎特伯雷语料（http://corpus.canterbury.ac.nz/），字符集大小分别为 63，100M128.txt是随机生成的100MB大小的文本，字符集大小为128。实验随机构建长度为m(5<=m<=50)模式串，长度间隔为5，每组测试的次数为10次取平均值，执行上述算法程序，统计出模式串不同长度时各算法的运行时间。

四种算法的运行时间图如下：

图3 100M文本运行时间图

从图2和图3的运行时间图可以看出，在字符集不大于128时，QS_I算法的运行时间明显低于QS算法、I_BMH2C算法和QSP算法，说明在此区域中，QS_I算法窗口平均右移量高于其他三个算法。QS_I算法预处理和匹配阶段的计算复杂度比I_BMH2C算法和QSP算法简单，在匹配阶段先只用模式串单字符P_WORD和文本字符T[j+pfi]进行比较，若不匹配可右移SHIFT_1+SHIFT_2两步，若两字符相等再引用QS匹配规则，所以QS_I算法的最大右移量为m+1+SHIFT_1。

4 结语

本文通过分析QS算法、I_BMH2C算法、QSP算法,并在QS算法的基础上提出一种改进算法——QS_I算法，QS_I算法不仅用单字符考虑当前窗口不匹配的可能性，还预测下次窗口移动的距离，模式串最大右移量为m+1+SHIFT_1，通过实验证明在字符集不大于128时，QS_I算法的运行效率明显高于其他算法。综上所述，QS_I算法提高了匹配效率，具有一定的应用前景。