基于改进Dijkstra算法的燃气应急模拟演练研究
2018-10-24谈亦豪王亚慧
谈亦豪 王亚慧
摘 要: 针对燃气突发事件应急处置中,应急处置人员需第一时间到达现场,城市道路最短路径搜索则是应急处置人员第一时间到达现场的关键,但考虑到实际路况较为复杂,若只提供一条最优路径,可能会因为临时交通管制等其他因素造成该条路段无法通行。通过引入时间权值及邻接矩阵及改进的Dijkstra算法进行最优路径搜索,为应急处置人员提供多条最短路径,并使用Anylogic软件对燃气突发事件泄漏事故应急处置情况进行模拟仿真,验证了Anylogic软件在燃气突发事件应急处置仿真评估应用的可行性。
关键词: 燃气突发事件; 应急处置; Dijkstra算法; 最优路径; Anylogic; 时间权值; 邻接矩阵
中图分类号: TN913.1?34 文献标识码: A 文章编号: 1004?373X(2018)20?0018?06
Abstract: During the emergency disposal of the gas emergency incident, the emergency disposal personnel need to arrive at the spot at the first time, and the shortest path search of the urban road is the key for the emergency disposal personnel to arrive at the spot at the first time. However, in consideration of the complexity of the actual road condition, if only one optimal path is provided, it is likely that this road section is not passable due to temporary traffic control or other factors. The optimal path search is conducted by introducing the time weight, adjacency matrix, and improved Dijkstra algorithm, so as to provide multiple shortest paths for emergency disposal personnel. The Anylogic software is adopted to conduct the emergency disposal simulation for the leakage accident of the gas emergency incident. The feasibility of applying the Anylogic software in the simulation evaluation for emergency disposal of gas emergency incidents is verified.
Keywords: gas emergency incident; emergency disposal; Dijkstra algorithm; optimal path; Anylogic; time weight; adjacency matrix
0 引 言
近年来我国发生重大及其以上的燃气安全事故数起,成为燃气行业面临的严重问题,当事故发生时,第一时间的应急处置则显得尤为重要。燃气应急处置人员能否在接到报警的第一时间赶到现场则是应急处置的关键。如今的城市交通道路路况复杂,以时间最短为目标可能存在多条最优路径,但基于目前燃气应急处置状况,基本上只提供一条最优路径,这往往会造成当所提供的最优路径因为临时的交通管制等其他原因而无法通行时,燃气应急处置人员无法快速地选择其余最优路径。所以为了避免上述情况的发生及综合城市交通道路实际情况,本文提出采用改进的Dijkstra最短路径搜索算法,为燃气应急处置人员提供多条最短路径,使燃氣处置人员可根据实时的道路状况进行最佳选择,在最短时间内到达事故现场,为应急处置争取黄金时间。同时也使用Anylogic软件对燃气突发事件泄漏事故应急处置进行仿真模拟,验证了Anylogic软件在燃气突发事件应急处置仿真评估应用的可行性。
1 Dijkstra最短路径算法
路径规划的核心是最短路径算法,研究最短路径的算法很多,如启发式搜索算法、神经网络方法、基于遗传算法、蚁群算法等的最短路径搜索。传统的最短路径搜索算法主要有Floyd算法和Dijkstra算法等。
Dijkstra算法是典型的单源最短路径算法,用于计算一个节点到其他所有节点的最短路径。它的主要特点一是以起始点为中心向外层层层扩展,直至扩展到终点;二是有代表性的最短路径算法,有较高的应用价值[1]。Dijkstra算法又称为双标号法。所谓双标号,就是对图中的点[vi]赋予两个标号[Pvi,λi]:第一个标号[Pvi]表示从起点[v1]到[vi]的最短路径长度;第二个标号[λi]表示在[v1]到[vi]的最短路径上[vi]前面一个邻接点的下标,即用来表示路径,从而可对终点到起始点进行反向追踪,找到[v1]到[vn]的最短路径。下面是Dijkstra算法的内容:
2 改进Dijkstra算法
在分析Dijkstra算法的基础上,可以看出Dijkstra算法默认为最短路径上某个顶点只有一个前置邻接点。但实际上,最短路径上某个顶点可能有多个邻接点,从源点出发到某一顶点之间,可能存在多条权重相同的最短路径。采用Dijkstra算法的改进,以解决多条路径最短问题。
2.1 邻接矩阵
为了更好地实现Dijkstra算法,用邻接矩阵表示无向带权图,设无向带权图[G1=V,E](见图1),顶点[V]的集合为[V=V1,V2,…,V5],边长[E=E1,E2,…,E6],则称5阶方阵为无向带权图的邻接矩阵如图2所示。
鄰接矩阵反映的是顶点与顶点之间的关系,矩阵的每个元素表示顶点之间边的权重。如果矩阵元素[aij]为[∞],那么说明两个顶点之间没有边直接相连;如果矩阵元素[aij]为一个正整数[ωij],那么说明两个顶点之间有一条边,边的权重为[ωij];如果矩阵元素[aij]为0,则说明邻接矩阵主对角线上元素全为0。
采用邻接矩阵表示带权图较为直观,并且Dijkstra算法需要多次修改顶点最短路径长度,用邻接矩阵表示带权图,矩阵中的元素也容易修改。
2.2 算法改进
本文采用的Dijkstra改进算法为文献[2]中提出的方法,主要解决了Dijkstra算法中多条最短路径问题与多邻接点问题,算法设计及改进如下:
1) 初始化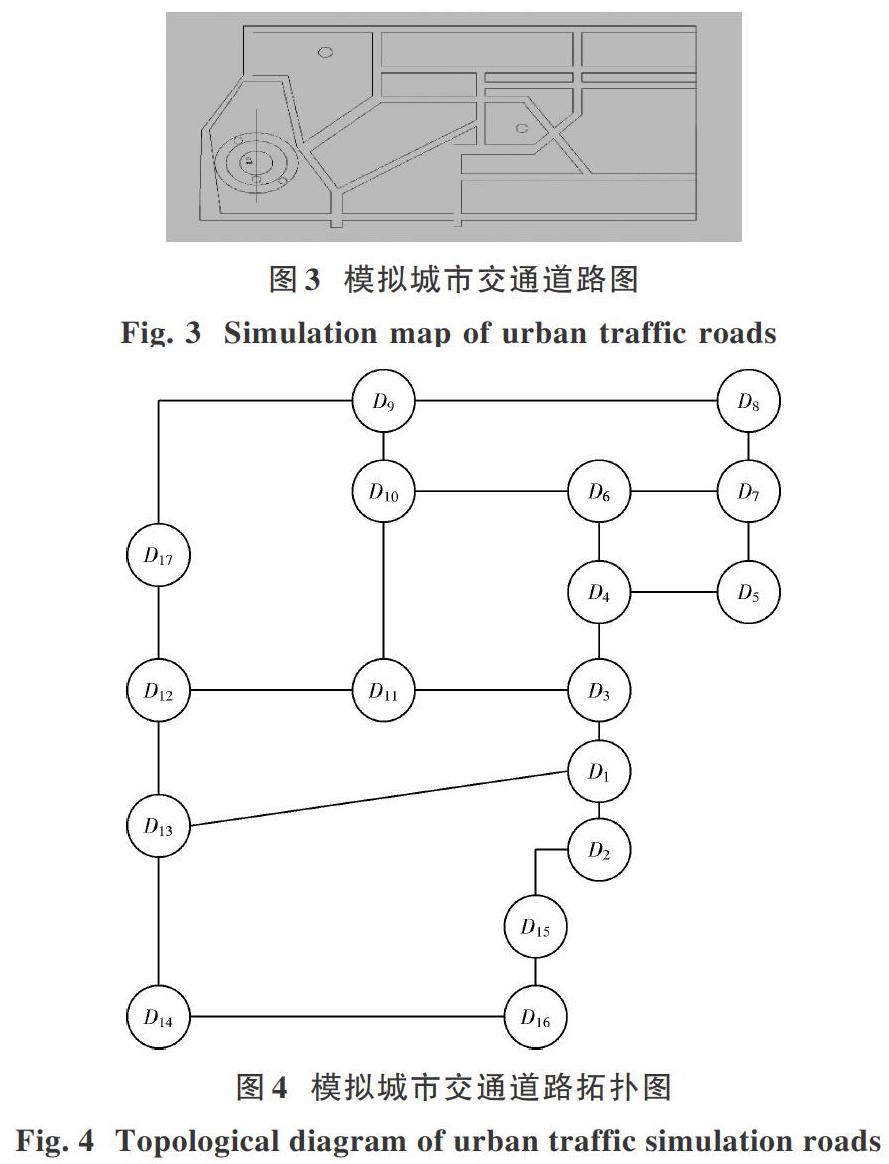
对所有顶点进行编号,并构造邻接矩阵。将起始点设定永久性标号(p标号),其余顶点都不是永久性标号。根据起始点,求起始点邻接点的最短路径,前面的邻接点及其个数。
2) 求下一个永久性标号(p标号)的顶点
通过邻接矩阵,找到没有永久性标号、最短路径长度最小的顶点v。如果顶点v的最短路径长度为无穷大,退出算法,否则,将顶点v设定永久性标号(p标号)。通过顶点v以及邻接矩阵,求顶点v的邻接点x的最短路径长度以及前面邻接点及其个数。如果起始点经过顶点v到邻接点x的路径长度小于邻接点x现有的最短路径长度,那么顶点x的最短路径长度为起始点经过顶点v再到顶点x的路径长度。
3) 求下一个永久性标号(p标号)的顶点,如果所有顶点都有永久性标号,退出程序[2],否则转步骤2)。
3 城市交通道路模型的构建
城市动态交通路径选择系统分为两个部分:其一是建立城市交通路径拓扑结构;其二是建立城市交通道路路径选择的数学模型。因实验时间等条件限制,模拟部分城市交通道路图,抽象出城市交通拓扑结构。模拟城市交通道路图如图3所示。
假设模拟城市交通道路图中道路相关信息,每条道路的相关信息主要包括:设计车速、路段名称、路段长度、道路的拥堵系数(用0和1来表示,0表示道路正常通行,1表示道路完全拥堵,无法通行)。本文采用路段长度与路段行驶时间相结合的选择路段的权值,若两个节点不连通,则两节点间距离为∞,本文采用∞来表示。其对应的路径拓扑结构如图4所示。其中节点表示交叉路口;单实线表示道路路段。
权值是道路某些特征属性的量化表示。因为权值是Dijkstra算法计算最短路径的依据,寻找最短路径即起点到终点之间的消耗最低,所以权值的确定是算法精确度的关键。本文设定每个路段来回方向上对应的权值相等,即每一条边都有且仅有一个权值。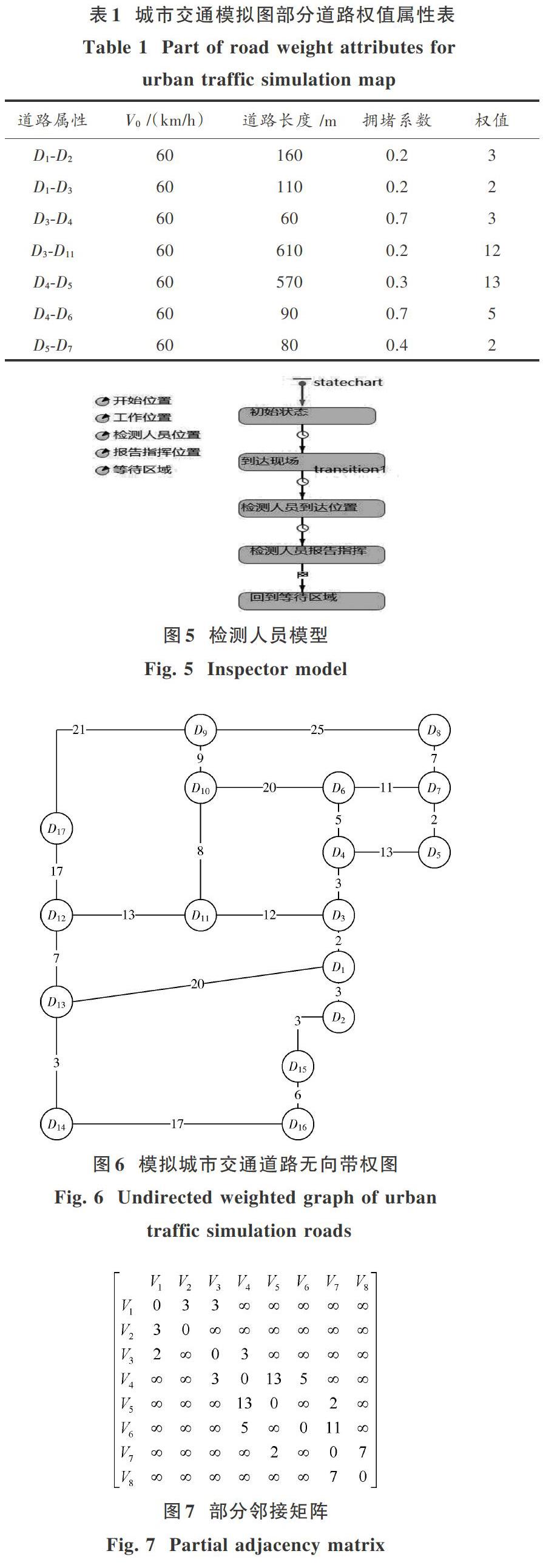
传统的Dijkstra算法中,权值仅表示2个节点之间的距离。由于城市交通道路,因受道路条件、道路绕行距离、交通条件的影响,使得不同的交通路径中,尽管车辆行驶的距离相同,所需的时间还是有一定差异的。所以通过城市交通道路的距离长短来判断是否是最优路径的方法不准确。本文主要解决燃气突发事件应急处置中的路径优化,是指应急处置人员在接到调度中心的指挥调度,由大队所在地赶往事故现场这一段路的路径优化过程。这个问题与一般路径优化问题不同的是需要考虑实际的路况环境,如道路拥堵程度、行车速度等。并且从应急的角度来讲,本文的最优路径搜索以时间最短为目标。故本文对权值的设定进行改进,以到达时间最短为准则,在考虑最优路径时,结合道路的距离、拥堵系数等确定权值,使最优路径搜索结果为时间最短的路径。经过调研研究发现,在排除突发事件影响的条件下,城市主干道路的每日拥堵情况类似,拟定在下列拥堵条件下进行算法实现。设定[QDi?Dj][i,j=1,2,…,17]表示道路[CDi?Dji,j=1,2,…,17](以下简写为道路C)的权值,[YDi?Dj][i,j=1,2,…,17]表示道路C的拥堵系数, [LDi?Dj][i,j=1,2,…,17]表示道路C的路径长度,[VDi?Dj][i,j=1,2,…,17]表示车辆的实际行驶速度,车辆行驶速度结合实际情况,假定每辆车正常行驶速度[V0]为60 km/h,则在不同的道路拥堵情况下,车辆行驶的速度公式为:
通过上述道路权值确定公式,确定模拟的城市交通道路图部分道路权值如表1所示。
4 Anylogic建模分析
4.1 应急抢修大队
应急抢修大队包含一般燃气突发事件应急处置所涉及的必需人员及车辆设备,其中包括指挥、控边、控压、泄漏点排查、泄漏检测、管线定位、管线修复、防腐层修复、土方作业、环境浓度监测几类人员。应急抢修大队当收到调度中心的抢修任务单时,需携带必要的抢修物资、车辆赶赴现场进行抢修。
4.2 燃气泄漏应急处置流程
燃气泄漏应急处置过程中主要包括以下几个步骤:浓度检测及环境监测、管道控压、控边及疏散、查漏定位、开挖亮管、制定方案、作业修复、收尾恢复等处置步骤。
4.3 Anylogic建模
在Anylogic中,对应急抢修大队应急处置模式进行建模分析,验证应急抢修大队应急处置模式的可行性。
根据燃气泄漏应急处置流程,将参与应急处置的人员及物资都分别用一个Agent代表,利用Agent理论对抢修流程进行建模,从而在Anylogic平台上搭建基于Multi?Agent的燃气泄漏应急处置模型。以检测定位人员模型建立为例,概括模型建立过程。建立检测定位人员模型,首先需明确在燃气泄漏应急处置流程中检测人员的职责及标准动作。职责及标准动作如下:
1) 接到抢修任务单后,跟随应急抢修大队赶赴事故现场;
2) 对现场泄漏位置的管线进行定位检测,确定管线信息;
3) 将检测结果报告指挥员;
4) 回到现场等待区域。
在Anylogic平台中,以城市交通道路图为背景,确定检测人员的行动位置,再以状态图的形式对检测人员进行建模,检测人员模型见图5。
5 Anylogic实验仿真
5.1 Anylogic中实现Dijkstra算法
为了验证Dijkstra最优路径算法在燃气泄漏应急处置中的有效性,在Anylogic平台上通过Java语言实现Dijkstra算法。以图3的城市交通模拟图为实验场景,假设D1为应急抢修大队所在地,D12为事故现场所在地。其中道路权值已经计算完成。 图6为城市交通道路无向带权图。
由图6可以清楚地看到每条道路的权值,可以看到道路D8?D9,D6?D10权值较大,是通过道路所用时间较长的路段。为了更好地研究和编程实现Dijkstra算法,用邻接矩阵表示图6城市交通道路无向带权图。图7是用邻接矩阵表示城市交通道路无向带权图的部分邻接矩阵。
运行最优路径算法起始顶点为D1,目标顶点为D12,得出两条最优路径,分别为:D1?D13?D12;D1?D3?D11?D12。
5.2 Anylogic燃气泄漏应急处置模拟演练
将燃气泄漏应急处置流程利用Anylogic平台进行模拟演练,验证了应急抢修大队及Anylogic软件在燃气突发事件应急处置仿真评估应用的可行性,并为燃气突发事件应急处置标准化工作提供支持。
Anylogic中燃气泄漏应急模拟演练的城市交通地图即为图3模拟城市交通地图。图8为Anglogic软件中进行燃气泄漏应急处置模拟的3D视图。
6 实验结果分析
在Anylogic软件中,以城市交通道路模拟图为背景,建立交通道路模型。根据道路长度、拥堵系数等参数确定道路的权值属性。确定属性后将城市交通道路图转换为无向带权图,并用邻接矩阵表示无向带权图。将邻接矩阵编入改进的Dijkatra算法程序中,在Anylogic软件中实现改进的Dijkstra算法。
在Anylogic中实现改进的Dijkstra算法,得出以下两条权值相同的最短路径,分别是:D1?D13?D12;D1?D3?D11?D12。图9中紫色所标示的为两条权值相同的最短路径。
为燃气应急处置人员提供了两条最优路径,当D1?D3?D11?D12其中一段道路因临时交通管制或其余突发状况造成道路较平常拥堵时,此时通过此段道路就要花费比平时要多的时间,这样燃气应急处置人员可根据实时路况选择最佳道路即D1?D13?D12出行。图10为Anylogic软件运行中燃气应急处置人员结合实际路况后沿着最优路径出发。
在Anylogic中运行改进的Dijkstra算法,得到两条权值相同的最优路径,而传统的Dijkstra算法默认一个最短路径上只有一个前置邻接点,只能得出一条最短路径的结果,若是遇到上述情况,则无法再给出其余最短路径结果。
在Anylogic软件中对应急抢修大队到达现场后的处置进行了模拟演练,证明了燃气泄漏应急处置流程的可行性,也验证了Anylogic软件在燃气突发事件应急处置仿真评估应用的可行性。具体抢修过程如图11所示。
7 结 论
针对燃气泄漏应急处置最优路径及基于Anylogic燃气泄漏应急处置模拟仿真,本文建立模拟城市交通道路的数学模型。引入时间权值及邻接矩阵的方法,采用对传统Dijkstra算法的改进,为燃气应急处置人员提供多条权值相同的最短路径,并利用改进后的Dijkstra算法结合燃气泄漏应急处置仿真模拟演练进行验证,规划了燃气应急处置人员到达事故现场前的多条最优路径。可以使燃气应急处置人员结合当时的路况情形进行最优路径的选择,同时验证了Anylogic在燃气突发事件应急处置仿真评估应用的可行性。
参考文献
[1] 袁琳,王渊,孙建芸,等.基于权值的Dijkstra停车路径规划算法的优化与实现[J].湖北大学学报(自然科学版),2017,39(3):279?284.
YUAN Lin, WANG Yuan, SUN Jianyun, et al. Optimizing Dijkstra algorithm design and accomplishment for parking routing programming based on weight calculation [J]. Journal of Hubei University (Natural science), 2017, 39(3): 279?284.
[2] 王树西,李安渝.Dijkstra算法中的多邻接点与多条最短路径问题[J].计算机科学,2014,41(6):217?224.
WANG Shuxi, LI Anyu. Multi?adjacent?vertexes and multi?shortest?paths problem of Dijkstra algorithm [J]. Computer science, 2014, 41(6): 217?224.
[3] 王宏.集装箱海铁联运最优路径算法设计与仿真[D].北京:北京交通大学,2017.
WANG Hong. Design and simulation of optimal path algorithm for container sea?rail transport [D]. Beijing: Beijing Jiaotong University, 2017.
[4] 段汝东,侯至群,朱大明.基于Java的Dijkstra最短路径算法实现[J].价值工程,2016,35(21):208?210.
DUAN Rudong, HOU Zhiqun, ZHU Daming. Implementation of Dijkstra shortest path algorithm based on Java [J]. Value engineering 2016, 35(21): 208?210.
[5] 闫倩.燃氣维抢修中的模拟演练和辅助决策关键因素及其相关性研究[D].北京:北京建筑大学,2015.
YAN Qian. Study on key factors and correlation of simulation drilling and aided decision?making in gas dimension rush repair [D]. Beijing: Beijing University of Civil Engineering and Architecture, 2015.
[6] 张旭凤.第三方物流企业配送网络演化规律及路径优化研究[D].北京:北京工业大学,2012.
ZHANG Xufeng. Research on evolution law and path optimization of distribution network of third party logistics enterprises [D]. Beijing: Beijing University of Technology, 2012.
[7] 刘超.燃气输配应急管理模拟系统研究[D].北京:北京建筑大学,2014.
LIU Chao. Study on emergency management simulation system for gas transmission and distribution [D]. Beijing: Beijing University of Civil Engineering and Architecture, 2014.
[8] MCNALLY P, MINYARD E. Emergency preparedness for oil and gas exploration and production [C]// Proceedings of SPE E&P; Health, Safety, Security and Environmental Conference. Denver: Society of Petroleum Engineers, 2015: 1?6.
[9] TERESCO J D. A Dijkstra′s algorithm shortest path assignment using the Google maps API: poster session [J]. Journal of computing sciences in colleges, 2010, 25(6): 253?255.
[10] 詹淑慧,杨光.城镇燃气安全管理[M].北京:中国建筑工业出版社,2007:60?66.
ZHAN Shuhui, YANG Guang. Safety management of town gas [M]. Beijing: China Architecture & Building Press, 2007: 60?66.
