防渗墙参数变化对坝坡稳定性的影响研究
2018-10-24吕良健
吕良健
(上饶市科信水利水电勘察设计咨询有限公司,江西上饶 334000)
0 引言
土石坝,作为水利工程中最为悠久的一种坝型,经过多年的发展,筑坝技术有了很大的提高,但是目前仍常发生大坝失事事故,主要原因为:地震、洪水漫顶、坝体渗漏及滑坡。其中滑坡和坝体渗漏是主要因素,均是因为水的因素。渗漏问题即是坝体内部发生开裂现象,在上游水压的作用下逐步发生扩展然后导致溃坝;而影响库岸边坡稳定性失稳破坏的重要因素是水作用,水不仅会软化岩土体,而且水的渗流作用会影响边坡内的渗流场变化,并随之影响岸坡的稳定性[1-2]。
对于病险水库,大部分都是因为渗漏问题进而需要进行加固,防渗墙是最可靠和有效的防渗措施,因而得到了广泛应用。对于覆盖层较厚的坝体,采用混凝土防渗墙作为防渗体更是一种经济有效的处理方式。如何合理地选择防渗墙的形式,以及对防渗墙应力变形分析,是工程中亟需解决的问题[3-10]。
目前,有限元分析已应用于土石坝及混凝土防渗墙的应力变形分析。陈剑等[3]从结构型式和接触面参数对防渗墙应力变形进行了分析;蒋定国等[4]研究认为“泥皮”在风化砂体和墙体之间起接触面作用,且摩擦系数很小;孙明权等[5]分析了不同的墙端约束形式、不同强度基岩及坝体材料对防渗墙应力变形的影响;马晓华等[6]研究了正常水位下防渗墙的应力和变形随坝体土料和防渗墙弹性模量变化而变化的规律,周爱兆等[7]通过4种不同接触面下混凝土防渗墙的受力变形特征得出了不同接触面单元对墙体应力变形计算结果的影响规律。
防渗墙的几何参数、材料参数对坝体稳定性均会有所影响,因此,如何合理选择防渗墙的厚度、如何合理选择混凝土防渗墙的计算参数,如何做到对其应力变形状态演变规律的掌握,无疑是此类工程设计所需要解决的关键问题。鉴于此,基于有限元数值模拟,对不同弹性模量、心墙厚度以及心墙位置的防渗墙坝体进行分析。
1 模型的建立及模型参数
在水库蓄水、大气降雨等不利因素作用下,某土石坝坝坡处于欠稳定~不稳定状态,可能产生滑移型、剥蚀侵蚀型破坏,产生塌岸破坏在所难免。因此,开展该段库岸的治理工作十分必要。
对研究区勘察资料进行整理,选取库岸的某个典型断面进行分析,对土石坝坝坡进行适当简化,坝坡简化结构图如图1所示。

图1 坝坡简化结构图
所研究的土石坝坝坡为带混凝土防渗墙的坝体,依据相关试验以及规范[11],对岩土体相关物理参数进行经验取值,表1为坝坡相关的物理力学参数。

表1 坝坡相关物理力学参数
利用Phase2有限元软件,对带混凝土防渗墙的坝体进行渗流和稳定性分析。
2 混凝土防渗墙参数渗流分析
2.1 渗流分析
对建立防渗墙前后的坝坡进行渗流分析,坝体孔压示意图见图2。

图2 坝体孔压示意图
从图2中可以看出,坝体中建有混凝土防渗墙后,孔压发生了明显的变化。建立防渗墙前,坝体的浸润线从上游坡面到下游坡面为一条直线,建立防渗墙后,坝体的浸润线在防渗墙处发生了突变,坝体上游的孔压几乎没有变化,浸润线也没有明显变化,但坝体下游土体孔压减小,浸润线也相应的降低。从孔压示意图中可以看出,建立防渗墙后下游坝体的浸润线明显降低,必然会对坝体稳定性产生影响。
2.2 应力分析
利用Phase2对建立防渗墙前后的坝坡进行应力分析,图3为竖向应力云图。

图3 坝体竖向应力云图
从图3中可以看出,建立防渗墙前,坝坡的竖向应力几乎为对称分布,建立防渗墙后,上下游坝坡的竖向应力有明显差异,但总体应力大小相差较小,最大应力均在坝坡底部,对中部岩土体的应力无明显影响。
3 防渗墙参数变化
3.1 弹性模量变化
混凝土防渗心墙的弹性模量变化,会对其刚度及扰度产生影响,分别对不同弹性模量情况下的土石坝进行分析,弹性模量为:35,25,15,1 GPa。表2为应力变形汇总表,因篇幅有限,只列举了弹性模量为15 GPa情况下位移及主应力分析图,见图4。
从表2和图5中可以看出,对于刚性的防渗心墙,随着弹性模量发生变化时,土石坝的水平位移和竖向位移变化很小,因此弹性模量对坝体的位移影响很小。对于不同弹性模量的防渗心墙,随着防渗心墙高度的增加,第一主应力和第三主应力的绝对值均呈现先增大后减小的趋势,说明防渗墙以受压为主。防渗心墙的弹性模量在15~25 GPa之间时,其应力水平较稳定,防渗墙结构较安全。
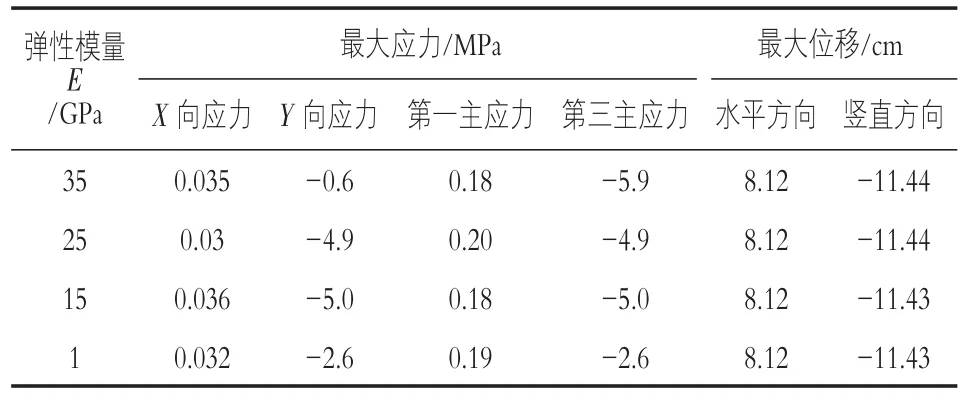
表2 不同弹性模量下坝体计算结果
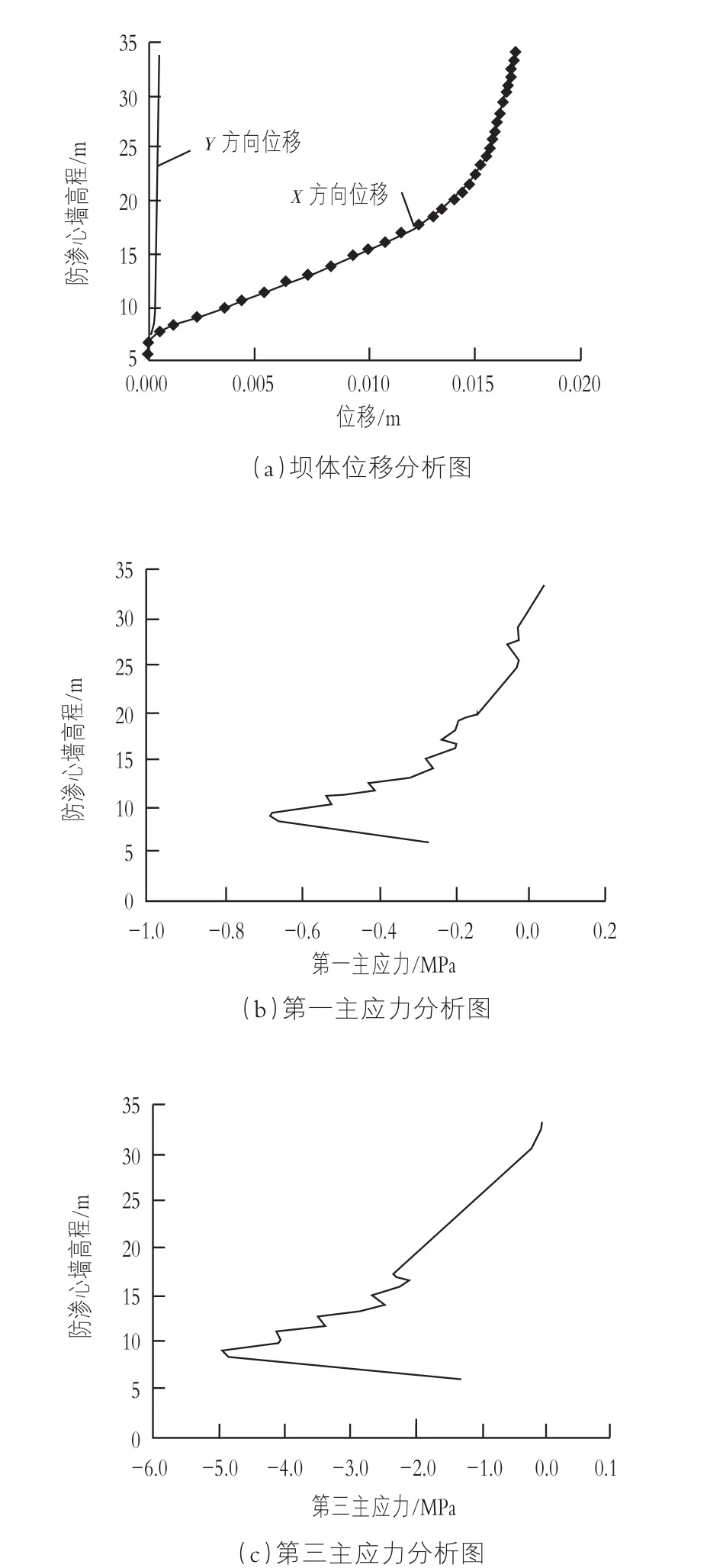
图4 弹性模量为15 kPa时坝体位移及主应力分析图
3.2 厚度变化
分别对不同厚度的混凝土防渗心墙对土石坝的影响进行分析,厚度为:40,60,80,100 cm,表3为应力变形汇总表,因篇幅有限,只列举了弹性模量为60 cm情况下位移及主应力分析图,图5为位移及主应力分析图。
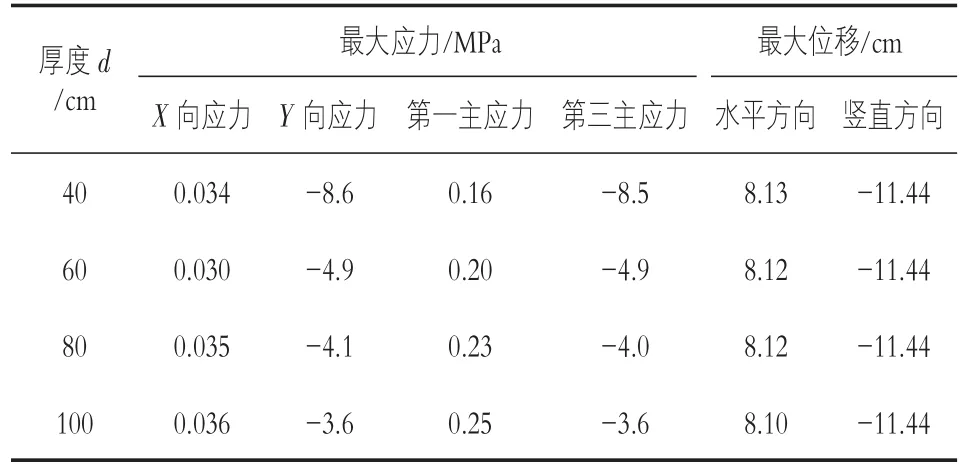
表3 防渗心墙不同厚度情况下坝体计算结果
从表3和图5中可以看出,随着混凝土防渗墙厚度发生变化时,土石坝的水平位移和竖向位移变化很小。防渗心墙的厚度越大,第一主应力越大,第三主应力的绝对值越小,随着防渗心墙高程的增加,第一主应力和第三主应力的绝对值呈现先增大后减小的趋势,并且均为负值,说明防渗墙以受压为主。防渗墙的厚度越大,第三主应力绝对值越小,压应力越小,结构相对较安全。
3.3 位置变化
分别对混凝土防渗心墙位置变化对土石坝的影响进行分析,防渗心墙距上游面坝顶的距离L为:2,3.6,6,8 m,表4为应力变形汇总表,因篇幅有限,只列举了防渗心墙距上游坝顶距离为6 m情况下位移及主应力分析图,图6为位移及主应力分析图。
从表4和图6中可以看出,随着防渗心墙位置发生变化时,土石坝的水平位移和竖向位移变化很小。防渗心墙离上游面坝顶距离越远时,第一主应力越大,第三主应力的绝对值越大,随着防渗心墙高度的增加,第一主应力和第三主应力呈波动变化,总体上其绝对值逐渐减小,且均为负值,防渗墙以受压为主。防渗墙的距上游坝顶距离越小,第三主应力绝对值越小,压应力越小,结构相对较安全。
4 结论

图5 厚度为60 cm时坝体位移及主应力分析图
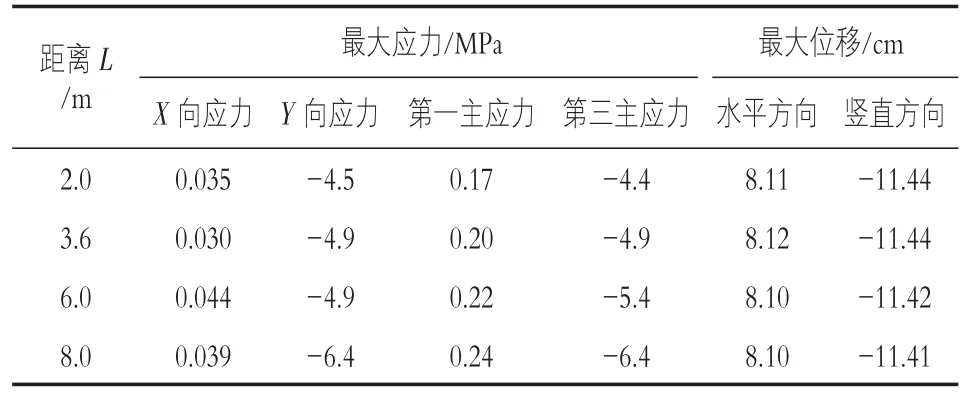
表4 不同防渗心墙位置下坝体计算结果
针对土石坝中常用的防渗心墙,采用有限元数值模拟手段,考虑不同弹性模量、心墙厚度、心墙位置等因素,对某土石坝实例进行了分析,得到以下结论:对于本算例,增加防渗墙的厚度,可以降低防渗墙的应力水平,结构相对更加安全;防渗墙的弹性模量在15~25 GPa之间时,防渗墙不会出现过大的压应力,其应力水平较稳定;防渗墙与上游坝顶面的距离越小,其应力水平相对越低,结构相对越安全。
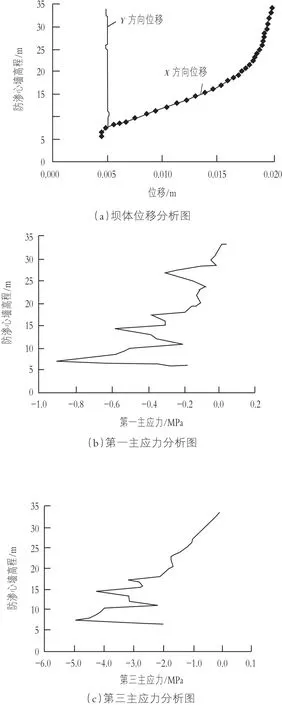
图6 防渗心墙距上游坝顶距离为6 m时坝体位移及主应力分析图
