巧用面积法求线段的和差

任 蕾

等腰三角形是轴对称图形中的“主角”，垂直是两直线特殊的位置关系，当它们遇到一起，会“碰撞”出什么“火花”呢？

【例】如图1，在△ABC中，AB=AC，P为底边BC上的一点，PD⊥AB于点D，PE⊥AC于点E，CF⊥AB于点F，那么PD+PE与CF相等吗？

图1

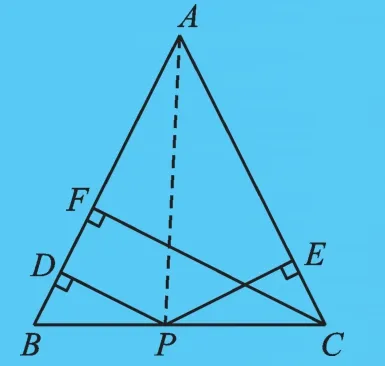
图2

乍一看，PD、PE、CF，这三条线段好像并无关系，怎么办？别慌，先想想题目中的条件能给我们什么帮助：垂直——三条关键线段都跟垂直有关系：垂直又意味着什么呢？对！垂直意味着高，就能求得面积！

显然，以FC为高，AB为底，可以表示△ABC的面积：S△ABC=

PD、PE可以看作哪个三角形的高呢？尝试连接AP，出现△ABP和△APC，它们的面积可以分别表示为：S△ABP=

记住——看见垂直想面积！FC、PD、PE分别出现在三个关系式中.可是，它们之间如何联系起来？显然，△ABP与△APC共同组成了△ABC，有等量关系：S△ABP+S△APC=S△ABC.

总之，看见垂直想面积，面积加减寻等量.我们用这两句口诀，做几个类似的尝试吧.

变式1.如图3，若P点在线段BC的延长线上运动，其他条件不变，你能尝试画出图形并找出PD、PE与CF之间的关系吗？

图3

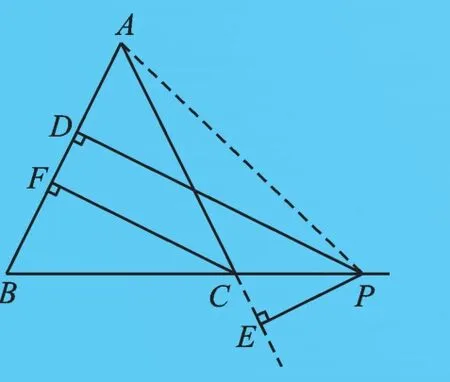
图4

显然，若点P运动到BC的延长线上，如图4，根据S△ABP-S△ACP=S△ABC及AB=AC可得PDPE=CF.

变式2.如果条件改为直线BC，其他条件均不变，PD、PE与CF之间的关系又将是什么呢？

变式3.如果把“等腰三角形”改成“等边三角形”，点P是三角形内任意一点（如图5），已知等边△ABC内任意一点P到各边距离分别为 d1、d2、d3，等边△ABC 的高为 h.你能求出 d1、d2、d3与h之间的关系吗？

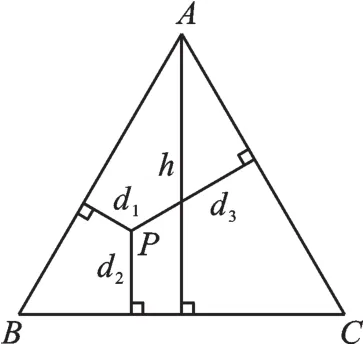
图5

图6

变式4.如果把变式3中的点P改成等边三角形外任意一点（如图6），其他条件都不变，你能求出d1、d2、d3与h之间的关系吗？

在几何问题中巧妙运用“面积法”，把线段关系转化为面积关系来解决问题是常用的思路，聪明的你学会了吗？

参考答案：

变式2.当点P在线段BC上时，同例题；当点P在线段BC延长线上时，同变式1；当点P在线段CB延长线上时，PE-PD=CF.

变式3.h=d1+d2+d3.

变式4.h=d1+d2-d3.