结合SIFT和Delaunay三角网的遥感图像配准算法①

祁 曦, 陈志云

(华东师范大学 计算机科学与软件工程学院, 上海 200062)

随着航空航天技术的不断进步和发展, 遥感影像不断向多时相、多角度及多分辨率方向发展[1]. 越来越多的科研人员开始对高分辨率遥感影像数据处理进行研究[2]. 而遥感影像快速配准就是这些处理中的关键一步. 遥感图像是由不同类型的传感器或从不同角度、不同时间对同一场景拍摄形成的, 所以遥感图像之间会存在几何变形, 给遥感图像处理带来一定的困难. 图像配准就是在对各类遥感数据进行处理之前, 先对两幅或多幅不同类型的图像进行空间几何变换, 使得图像中代表同一位置的对应区域映射到相同坐标下, 而后进行匹配或叠加.

目前主要有两类图像配准方法:一类是基于灰度的配准方法, 另一类是基于特征的配准方法[3]. 基于灰度的配准方法主要是比较两幅图像的灰度相似性, 找出相似度高的区域[4]. 该方法对图像灰度的依赖程度很高, 运算量比较大, 对图像灰度差异大、图像旋转、图像噪声等情况的处理效果不佳[5]. 代表方法有最大互信息法[6]、傅里叶变换[7]等. 基于特征的图像配准方法是匹配两幅图像中的共性显著点, 它大大地降低了计算量, 且由于只关注图像的局部, 所以对图像的灰度变化、遮挡都有较好的不变性[8]. 该方法一般选取遥感影像的点、线、区域等特征, 而其中特征点的提取相对于线、区域特征来说, 既可以保证图像的信息量, 又能降低自身的数据量, 且提取容易, 不易受光照、尺度、旋转等图像变化的影响[9]. 因此基于点特征的方法已成为国内外学者的研究重点. 常用的点特征提取算子有SIFT 算子[10]、Moravec 算子[11]、Harris算子[12]、SURF算子[13]、SUSAN算子[14]等. 其中公认最好的点特征提取算子是Lowe于1999年提出并于2004年改善形成的SIFT算子[10]. 相比于其他算子, SIFT算子具有较好的亮度、尺度、旋转不变性, 且对仿射变换、视角变化、噪声保持一定的稳定性. 但是SIFT算法也有计算量大、实时性差、存在误配点等问题. 樊东昊等人[15]针对SIFT算法提取的特征点数目量大且正确匹配点率不高的问题, 提出了一种基于区域选择和SIFT的配准算法, 避免提取冗余特征点, 提高正确匹配率且加快配准速度. 冷成财等人[8]针对基于SIFT算法的遥感影像配准过程中产生误配点且遗漏正确匹配点的问题, 提出了一种改进的SIFT配准算法, 即SODCSIFT算法, 提高正确匹配点对数量且提升配准精度. 李孚煜等人[16]则对基于SIFT的遥感图像配准算法进行了总结概述, 并对各类算法的优缺点进行了详述.

对高分辨率遥感影像来说, 地物细节信息更加丰富, 因此易受拍摄角度、时相等影响, 比如建筑物等,在传感器从不同角度拍摄时, 该物体形状、位置以及阴影区域等会发生不同程度的变化. 由于建筑物的高度变化和阴影区域的不同, 会影响特征点的准确提取和有效匹配, 容易出现误匹配点, 降低图像的配准精度[17].同时为了消除高分辨率影像中的局部几何变形, 也需要提取恰当数量且均匀分布的特征点. 马旭燕等人[18]针对高分辨遥感影像中控制点数目多且分布不均的问题, 提出了SIFT和MSER(极大稳定区域)结合图像分块的配准算法, 剔除冗余特征点且改善特征点分布的均匀性. 程国华等人[19]针对遥感影像本身匹配方法单一且特征点分布不均的问题, 在改进Harris算子的基础上, 结合分块迭代剔除策略和小三角形面元TIN, 完成了影像配准.

针对高分辨率遥感图像数据量大且易出现误配点的问题, 本文提出了一种基于SIFT和Delaunay三角网的高分辨率遥感图像配准方法. 下文首先介绍了SIFT算法、图像分块和Delaunay三角剖分的原理, 然后描述了高分辨率遥感图像配准改进算法的具体步骤,之后对配准实验结果进行分析并得出结论, 最后对本文算法进行总结和展望.

1 相关术语

1.1 SIFT配准原理

SITF算法是由David G. Lowe于1999年提出, 并在2004年加以完善. Lowe将尺度的概念引入到SIFT算法中, 利用SIFT方法检测图像特征点的实质就是在不同尺度空间上查找特征点, 这些特征点对应的就是不同尺寸的地物[17]. 而在高分辨影像中, 往往就是较小尺寸的地物会容易发生变化, 如房屋、汽车等等, 因此为了减少这些小尺寸地物对特征点提取的影响, 那么就要分尺寸的对图像中的地物进行分析.SIFT配准方法主要分为四步:尺度空间的建立, 尺度空间中提取关键点, 生成特征点描述子, 特征点匹配.

(1) 尺度空间的构建:SIFT算法用函数L(x,y,σ)来表示图像的尺度空间, 用函数I(x,y)表示遥感图像, 则尺度空间就是由图像I(x,y)和高斯函数G(x,y,σ)卷积生成的, 公式为:

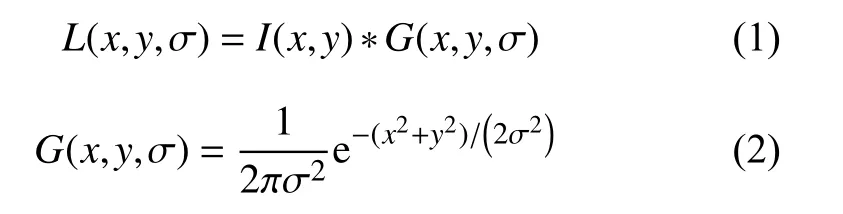
其中, *指的是在x方向和y方向上进行卷积操作, σ表示尺度空间坐标.

为了检测稳定特征点的位置, SIFT算法用DOG尺度空间来代替LOG尺度函数. 通过对两幅相邻高斯尺度空间图像相减, 得到DOG尺度空间, 该尺度空间的计算公式如下:

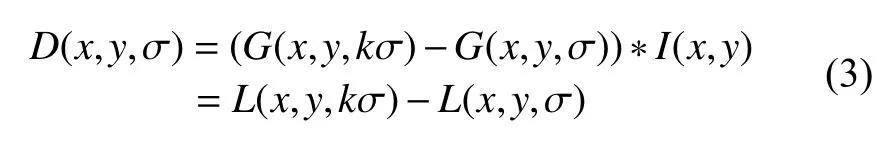
(2) 尺度空间中提取特征点:尺度空间中的所有检测点都与其同尺度相邻的8个点和上下尺度各相邻的9个点进行比较, 只保留局部极值点. 之后去除其中不好的关键点, 通过子像元插值和剔除对比度低的点以及不稳定的边缘响应点来对精化检测到的关键点.

(3) 生成特征点描述子:在以关键点为中心的邻域窗口内采样, 计算邻域内各像元的梯度幅值和梯度方向, 并用梯度方向直方图来统计邻域内像元的梯度方向, 则关键点的主方向就是直方图的峰值. 之后将坐标轴旋转为特征点的方向, 以确保旋转不变性, 然后对特征点周围区域进行分块, 分为 4 ×4个子区域, 对每个块内的梯度方向进行统计, 得到8个方向的梯度方向直方图, 最终形成128维的SIFT特征向量.

(4) 特征点匹配:使用欧氏距离来判断两幅图像特征点的相似性. 在匹配过程中, SIFT算法使用的是Kdtree算法, 即找出待配准图像中与参考图像特征点A距离最近的点B和距离次近的点C, 将最近邻和次近邻距离相比, 若比值小于给定的阈值, 则认为匹配正确, 特征点A与B是一对匹配点.

1.2 图像分块策略

在提取特征点之前对图像进行分块处理, 有助于改善特征点提取的均匀性, 对图像进行分块有两种方式:

(1) 第一种方式是预先设定图像块的边长, 然后对整幅图像分块. 适用于块数未知的情况.

(2) 第二种方式是预先设定好划分的块数, 根据块数来对整幅图像进行分块. 通常可划分 2 ×2、4×4 8×8等.

本文采用的就是第一种方式, 定义划分的子块图像大小为n1×n2, 而这些划分的子块图像之间有一小部分是重叠的, 因为SIFT没有办法提取图像边缘的特征点, 重叠区域的宽度定义为oval.

1.3 Delaunay三角形相似函数

现在的三角形剖分技术已日趋成熟, 因为其构建的三角网灵活性大且能较好逼近边界, 所以广泛应用于测绘学、地质学、地理学和图像学等领域中.Delaunay三角形剖分就是其中一项比较重要的三角形剖分技术[20]. Delaunay三角形剖分有最大化最小角和空外接圆两个特性, 可以有效的避免常规三角剖分所带来的病态三角形的问题.

三角网的构建一般有三个算法:分治算法、三角形生长法和逐点插入算法. 由于三角网生长法搜索效率低, 不适合海量数据的搜索建网, 分治算法效率很高但会占用大量内存, 而逐点插入算法实现简单且占用内存较少, 因此成为本文构建三角网的首选算法[20].

构建完三角网之后, 就要对三角形进行相似度比较, 以确定相互匹配的特征点[20]. 假设需要判断相似性的两个三角形分别为 ∆ABC和∆A′B′C′, 其中A、B、C和A′、B′、C′分别为对应的点对. 还假设两个三角形之间的相似度为I, 三个对应角度之间的相似度分别为Ia、Ib和Ic, 角A的值为a, 角A′的值为a′, 则角A和角A′的相似度公式为:

在这里, σ =a/6.

之后再分别求另两对内角的相似度Ib和Ic, 则∆ABC和∆A′B′C′为:

之后定义参数s, 把该参数作为判断两个三角形是否相似的标准, 即如果计算出的两个三角形的相似度I≥s, 则这两个三边形是相似三角形, 否则两个三角形并不相似.

算法对三角网中的所有三角形进行相似度计算,并构造一个相似度矩阵D, 从中寻找相似度大于等于参数s的元素, 则该元素所对应的三角形对就是相匹配的三角形, 以此得到精确匹配点对.

2 高分辨率遥感图像配准改进算法

2.1 算法思路

本文配准算法的具体步骤如下:

(1) 对图像降采样后利用SIFT算法对图像进行粗配准. 因为单幅高分辨率图像的数据量很大, 所以从图像上提取的特征点数目很多, 如果直接利用这些特征点进行配准的话, 会增加计算量, 影响配准速度, 还容易造成误匹配, 从而降低配准精度. 因此, 在进行配准之前, 先对图像进行降采样处理, 然后利用SIFT算法提取两幅降采样图像的特征点. 通过对SIFT算法进行分析发现, 该算法中低尺度层的特征点往往对应的是高分辨率图像中较小尺寸地物, 比如城市区域中的建筑物等, 由于尺寸较小的地物在高分辨率图像中容易发生变化, 所以这类特征点的提取一般容易出现错误;而算法中的高尺度层的特征点则对应的是一些尺寸比较大的地方, 比如说大面积的草坪、广场等等, 这类特征点一般比较稳定, 不会轻易的就发生变化[17]. 所以本文在进行粗配准时, 选用的就是这些比较稳定的特征点. 首先在进行SIFT尺度空间构建时, 把第三组及其以上尺度空间的特征点作为该尺度空间的高尺度特征点, 其它尺度空间的特征点作为该尺度空间的低尺度特征点. 选择高尺度空间的特征点进行特征匹配工作,寻找待配准图像中与参考图像中特征点的距离最近与次近的特征点, 求得最近距离与次近距离的比值, 并将该值与给定阈值进行比较来得到匹配点对. 最后使用这些匹配点求得仿射变换模型, 对图像进行几何校正,完成图像粗配准.

(2) 在图像分块的基础上提取特征点, 并完成初始匹配. 在上一步之后, 得到了待精配准图像和基准图像,之后对这两幅图像进行精配准工作. 首先对两幅图像进行分块, 因为之前已对图像进行了粗配准, 所以此处对应位置的子块图像构成一组图像子块对, 之后分别对各组图像子块对进行特征点提取和匹配工作. 在这里使用的是SIFT算法对子块图像提取特征点, 完成初始匹配工作, 得到初始匹配点对.

(3) 构建Delaunay三角网, 利用三角形相似函数获得精确匹配点对. 首先使用逐点插入算法进行Delaunay三角形剖分, 得到三角形网. 之后针对三角形网使用三角形相似函数来度量三角网中所有三角形对之间的相似度, 构建相似度矩阵, 从中选取相似度大于等于判断标准s的三角形对作为候选三角形对, 该三角形对所对应的顶点对就是精确匹配点对. 本文对这一步的改进之处在于求解三角形对之间相似性时, 不需要计算整幅图像三角形之间的相似度, 而是利用第二步的图像分块, 分别在子图像上构建三角网, 然后计算一组图像子块对之间的三角形相似度矩阵这样可以大大减少计算量, 提高匹配效率. 最后得到了每组子图像对之间的精确匹配点对, 然后把这些子图像匹配点对的坐标转化为分块之前图像中点的坐标, 以便之后进行整幅图像的精配准.

(4) 在获得精确匹配点对之后, 进行仿射模型变换,求解空间变换模型, 对图像进行几何校正, 完成最终的图像配准.

根据上述算法步骤, 总结算法具体流程如图1所示.

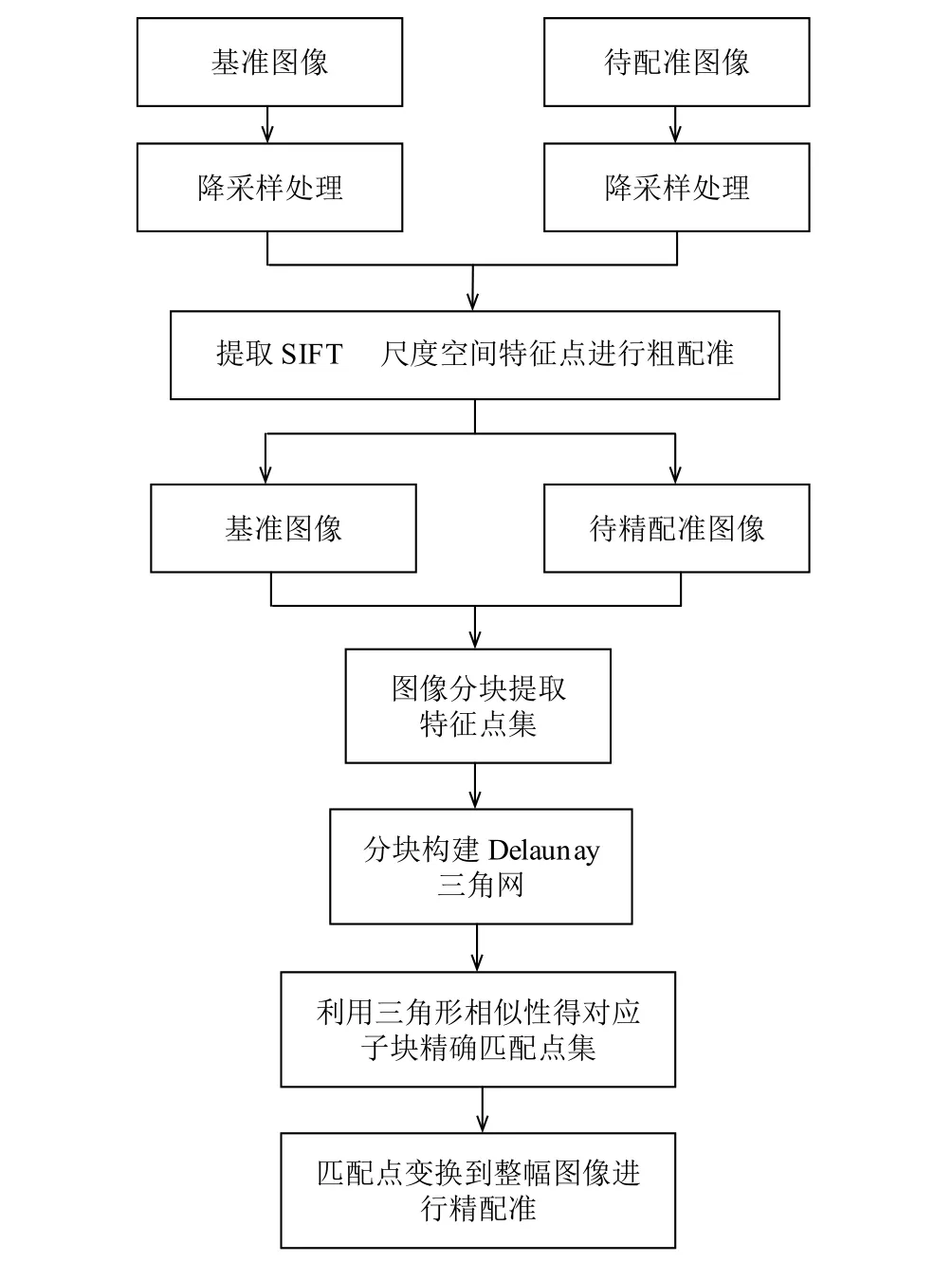
图1 改进算法流程图

2.2 评价标准

本文采用CMR和RMSE作为评价指标对配准精确度进行描述.

其中, 公式(7)中,N是参与匹配的特征点个数,n是正确匹配点个数, 则CMR求得的是正确匹配点率.CMR越大, 正确匹配点率越高, 那么用该匹配点对求得的转换模型就越精确, 配准精度也就越高. 公式(8)、(9)、(10)中,t11、t12、t21、t22、tx和ty分别是求得的仿射变换模型的参数;(x1i,y1i)是基准图像的特征点坐标, (x2i,y2i)是与基准图像相对应的待精配准图像特征点坐标, 而(x1i′,y1i′)是待精配准图像图像的特征点进行仿射变换后求得的点坐标. 那么RMSE公式的含义就是利用求得的转换模型参数, 计算待精配准图像坐标经过准换后的坐标值, 并将其与基准图像的坐标值进行比较, 求两者的标准误差来评价配准的精确度. 在这里用RMSE来衡量配准精度,RMSE的值越小, 配准精度越高.

3 配准实验结果及分析

3.1 实验数据和实验环境

本文的实验数据是由三组城市区域遥感卫星图像组成, 第一组是OVS-1A/B卫星于2017拍摄的美国达拉斯市区遥感影像, 全色图像分辨率为1.98米, 多光谱图像分辨率也为1.98米, 图像大小为3396× 2644. 第二组是lUtraCam-D卫星于2005年拍摄的伊朗首都德黑兰的两幅RGB图, 两幅图像的大小都为1256× 1278.第三组图像也是由lUtraCam-D卫星于2005年拍摄的伊朗首都德黑兰的两幅RGB图, 两幅图像大小为1161× 1169. 图2是本文实验数据图.

本实验是在Windows 10操作系统的运行环境中完成的, 计算机配置是Intel(R)Core(TM) i5-7200U 2.50 GHz CPU, 内存8 GB, 使用Matlab 2013a软件实现编程运行.

3.2 实验结果及分析

3.2.1 实验分析过程

本文针对以下几个问题进行了对比实验:

首先针对三组图像, 分别使用SIFT算法和本文算法提取特征点, 比较两种方法提取特征点数目的不同.分析本文算法与SIFT, 得出两种方法在计算量上的差异.

其次针对三角形相似度判断标准s的合适取值问题, 对s不同取值下获得的正确匹配点率进行实验对比, 找出恰当的参数大小.

再次针对匹配阶段获得精确匹配点对的问题, 对Delaunay三角形剖分和传统方法使用的RANSAC(随机采样一致性)算法进行对比实验, 分析两种算法的正确匹配点率, 得出最佳匹配算法.

最后对本文改进算法和传统SIFT算法的配准精度进行评价, 显示最终的配准效果图.

图2 实验数据图

3.2.2 实验对比结果

首先是对图像提取特征点的工作. 对三组图像分别用传统SIFT算法和本文算法提取特征点, 比较两种算法在特征点提取上的不同. 图3(a)是第一组遥感图像分别使用SIFT和本文算法提取特征点图;图3(b)是第二组图像分别使用SIFT和本文算法提取的特征点图;图3(c)是第三组图像分别使用SIFT和本文算法提取的特征点图. 从图中可以看出, 传统SIFT算法提取的特征点数目过多, 三组图像提取的特征点数分别是5546、1088和760个特征点;而使用本文算法对三组图像提取特征点数目分别为2559、719、521. 通过比较分析可以得出, 本文算法确实大大减少了提取的特征点数目, 减少了计算量, 降低了计算复杂度.

实验中, 本文使用的分块大小是n1=512,n2=424, 预留边界的大小是15%的分块大小. 在三角形相似度计算中, 对参数s的设定进行了试验分析, 分析结果如表1.

从表1中可以看出, 参数s的适合大小是0.75. 本文不同参数提取的特征点数目相差不大, 但是当参数大于0.75时, 正确匹配点率虽然会高, 但是正确匹配点的数目是逐渐减少的, 当参数小于0.75时, 会提取出较多的错误匹配点, 所以选择了一个恰当的参数0.75.

表1 使用不同参数s的匹配结果

其次在特征点匹配工作上, 本文利用三角形相似度度量的方法与RANSAC算法进行了对比实验, 结果如图4和图5所示, 图4(a)是对第一组图像使用传统SIFT算法使用RANSAC算法之后得到的精确匹配点,图4(b)是它的连线图. 而图5是本文算法中, 使用RANSAC算法和Delaunay三角形剖分得到的精确匹配点的对比图. 图5(a)和(b)是第一组和第三组图像得到的待精配准图像与基准图像, 图5(c)和(d)是本文算法对第一组和第三组图像分块子图像使用RANSAC算法后的匹配点图, 图5(e)和(f)是对第一组和第三组图像相同的子图像对使用Delauany三角剖分构建了的三角网图像, 图5(g)和(h)是对第一组和第三组图像进行三角形相似度度量得到的精确匹配点. 可以看出, 本文算法使用Delaunay三角剖分进行精确匹配后,误匹配点的数目减少了, 且正确匹配点数目比RANSAC算法得到的正确匹配点数目多. 表2、表3分别是第一和第三组图像在提取精确匹配点时, 使用RANSAC算法和Delaunay三角形剖分得到的精确匹配点结果对比.

图4 使用传统SIFT算法得到的匹配点及其连线图

图5 使用RANSAC和Delaunay三角剖分分别进行匹配点配对的效果图

表2 第一组图像使用RANSAC和Delaunay方法提取正确匹配点对比

表3 第三组图像使用RANSAC和Delaunay方法提取正确匹配点对比

从表中可以看出, 使用Delaunay三角形剖分提取的精确匹配点数目多且减少了误匹配点的数目.

最后计算SIFT算法和本文算法的RMSE和CMR,可以得到, 第一组图像使用SIFT算法的正确匹配点率为91.33%, 本文算法的正确匹配点率为97.48%;第三组图像使用SIFT算法的正确匹配点率为81.25%, 本文算法的正确匹配点率为93.18%, 说明本文算法的正确匹配点率高于传统SIFT算法. 而第一组图像使用本文算法的RMSE为1.76, 传统SIFT算法得到的RMSE为3.15;第三组图像使用本文算法的RMSE为1.28, 传统SIFT算法得到的RMSE为2.56, 说明本文算法的配准精度高于传统SIFT算法. 表4、表5分别为第一组和第三组图像使用SIFT算法和本文算法的RMSE、CMR以及运行时间的对比. 从表中可以看出,本文算法运行时间比SIFT较小. 图6是本文最终配准结果图.

表4 第一组图像本文方法与SIFT方法的精度评价

表5 第三组图像本文方法与SIFT方法的精度评价

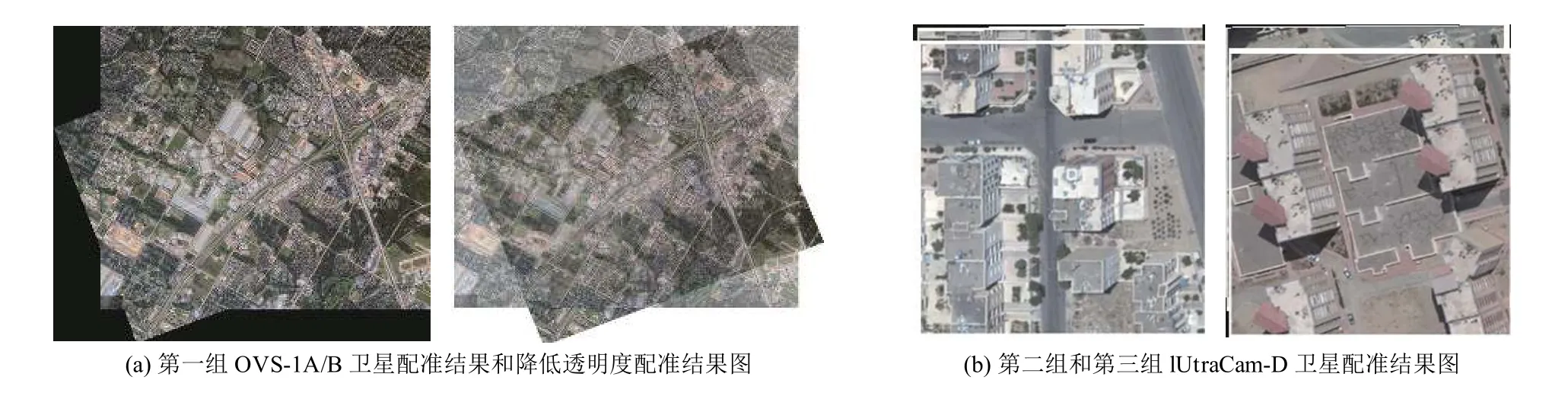
图6 配准结果图

4 结论与展望

针对高分辨率遥感图像配准中图像本身数据量过大且存在误匹配点的问题, 本文提出了一种基于SIFT和Delaunay三角网的高分辨率遥感图像配准方法, 该方法分为粗配准和精配准两个阶段. 为了降低高分辨率遥感图像本身的数据量, 在进行配准工作之前采用降采样方法处理两幅图像. 之后仅提取高尺度空间下的SIFT特征点用于粗配准. 之后进入精配准阶段,为了提取均匀分布的特征点, 本文引入了图像分块策略, 对待精配准图像进行图像分块. 之后对每幅子块图像提取特征点并构建Delaunay三角网, 利用三角形相似函数求得精确匹配点对, 然后将得到的子匹配点对坐标转化为分块之前图像中点的坐标, 以便进行整幅图像的精配准工作. 从实验中可以看出, 该算法提取的特征点是减少的, 且算法的正确匹配点率要大于传统SIFT算法得到的正确匹配点率, 因此, 本文算法配准精度更高. 但是受实验数据的限制, 本文只是针对城市建筑物区域遥感卫星像进行实验, 并未对非城市建筑物图像或其他类别图像进行实验, 且算法速率也有待于进一步优化.