侧壁悬挂雷达多维隔振平台性能仿真及实验

董迎晖,方 辉，黄 宵

(1.合肥工业大学 机械工程学院,合肥 230000；2.中国电子科技集团 第三十八集团,合肥 230000)

机载雷达的精度和工作能力直接影响到飞机性能。飞机发动机以及飞机起飞、降落和正常巡航时的自身、外界等原因引起的机身振动对机载雷达的影响越来越被人们重视，如何减少振动对机载雷达的危害已成为机载设备隔振领域的一个重要研究方向。

目前，对于隔振技术研究方向可以分为三种类型：主动隔振式、被动隔振式以及主被动隔振一体化[1]。其目的均是通过隔振装置减少“振源”对设备的振动影响[2]。金属橡胶隔振器[3]、空气弹簧隔振器[4]均具有较好的隔振效果。但是，不适宜用在侧壁式机载雷达隔振。被动隔振相对于其他两种隔振类型，具有结构简单、无需额外供能和较高的可靠性等优点，对于载机具有很大的优势。传统的被动隔振对于侧壁式机载雷达多维隔振无法有效地满足其多维隔振的要求。因此，隔振维度由单一维度逐步发展到多维隔振[5]，隔振器由线性发展到非线性隔振器[6]。目前的被动隔振技术研究方向主要集中在阻尼技术和隔振器设计与应用上。

近年来，不少学者将多维隔振和并联机构结合在一起进行研究并取得了显著的成果。美国弹道防御组织[7]针对红外望远镜设计了振动隔离抑制系统VISS，有效减少振动对望远镜的影响，提高了望远镜的成像质量；于大国，马履中等人[8]将基于Stewart结构的多维被动隔振装置应用于车辆隔振中，获得了良好的隔振效果；2004年马履中教授在《多维减振平台主体机构的分析研究》[9]提出的将多自由度并联机构作为基础结合弹性阻尼元件进行隔振的设想较好地解决了多自由度隔振问题。王晓雷，杨庆俊等人[10]提出一种采用8作动器的多维隔振平台，相比较于传统的6杆Stewart机构[11]，8杆机构具有更好的失效保护能力，董迎晖等人提出一种8杆机载雷达多维隔振平台具有失效隔振性能[12]。

基于并联机构的被动隔振技术的研究成果虽然较多，但大多用于地面隔振且位姿是垂直于地面，对于侧壁悬挂式安装方式以及航空环境下隔振性能还仍需要做进一步的分析研究。本文为了满足航空航天环境下侧壁悬挂式多维雷达隔振要求，设计了一种基于并联机构的被动隔振平台，满足机载雷达在航空航天环境下的隔振要求。

1 侧壁悬挂雷达多维隔振平台设计

1.1 隔振平台设计参数及要求

某型号雷达阵面面积为1 372 mm×500 mm、质量为110 kg、雷达与机舱壁之间最大距离为350 mm、固有频率为110 Hz；被动隔振平台雷达端允许安装区域为1 372 mm×500 mm的矩形、机舱壁端允许安装区域为1 372 mm×586 mm的矩形，矩形区域厚均为50 mm。

隔振平台一端以10°倾角侧壁式安装在载机侧壁，另一端连接雷达。该隔振平台在承载侧壁式雷达自重实现隔振的目的时，对隔振杆中的隔振器提出拉压双向隔振的要求。同时，在侧壁式安装于载机时要具有六维隔振能力，隔振平台的机构需要具有6自由度，实现多维隔振的要求。

1.2 隔振平台结构设计及自由度计算

基于1.1中已知隔振平台设计参数及要求，侧壁式多维隔振平台采用8杆并联机构，在每根杆中串联双向金属弹簧阻尼隔振器。隔振平台机构简图如图1所示。

8杆并联机构中的每根杆均有两个球副和一个移动副组成。两个球副均通过TBS关节轴承来实现转动；移动副是处在两个球副之间，通过串联在每根隔振杆中的双向弹簧隔振器实现移动。

隔振平台单根隔振杆的结构示意图，如图2所示。

由螺旋理论，运动支链中每个球副用三个轴线相互垂直的转动副代替，则支链在初始位置的运动螺旋可表示为公式（1）所示。

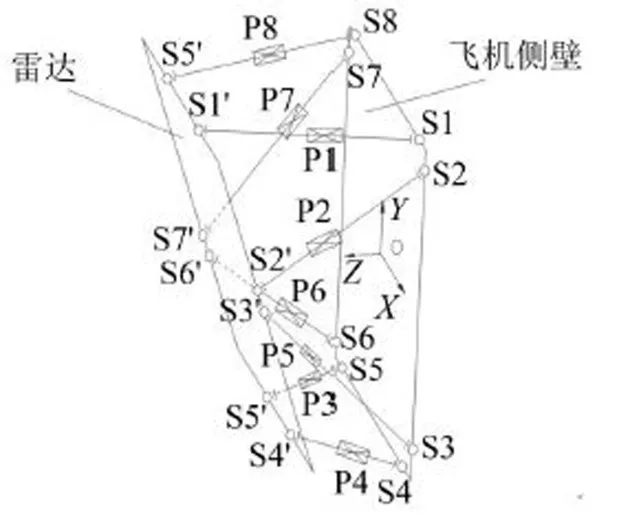
图1 侧壁式隔振平台机构简图

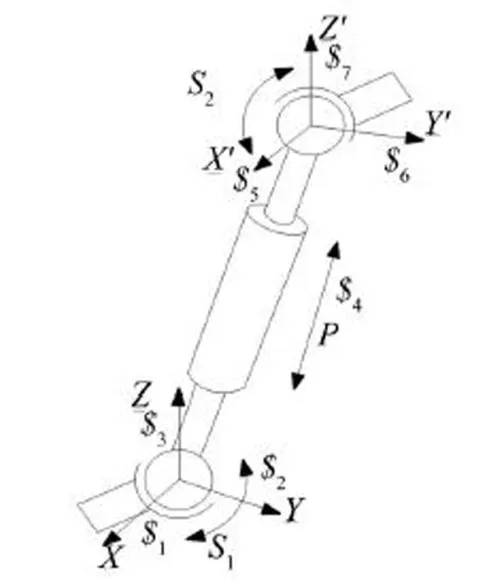
图2 隔振杆示意图

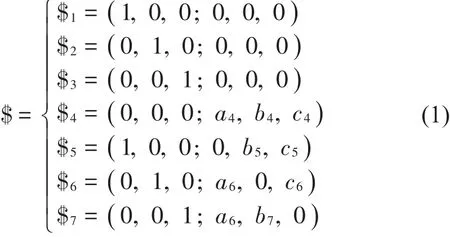
该支链的运动螺旋系线性相关，且秩为6，所以该支链的反螺旋系不存在；隔振平台整体机构不产生公共约束，即λ=0，则机构阶数d为6；每一条支链中都含有一个局部自由度，整个机构共含有8个局部自由度。

根据修正的Kutzbach-Grubler自由度计算公式。

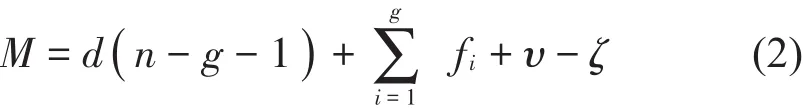
其中：d表示机构的阶数，n为构件数，g为运动副数，fi为第i个运动副自由度数，υ为并联机构附加冗余约束，ζ为机构中存在的局部自由度。

由式（1）和式（2）可知M=（18-24-1）+56-8=6，即8杆并联隔振机构的自由度数为6。

1.3 侧壁悬挂隔振器设计

由1.1节隔振平台以10°倾角侧壁式安装在载机侧壁可知，要求隔振平台在承载悬挂雷达自重条件下实现隔振。因此，这就需要平台中耗能元件隔振器具有双向减振的功能，即在预应力为受拉（或受压）条件下仍可实现隔振。我们设计了一种双向弹簧隔振器，如图3所示。

图3 双向弹簧隔振器

单个隔振器的重量为1.06 kg、外观尺寸为150 mm×50 mm×50 mm、最大拉压行程设计为10 mm、刚度和阻尼值依据平台隔振性能要求分别选择350 N/mm和3.5 Ns/mm（传递率小于等于1.995倍）。

2 隔振平台仿真分析

2.1 隔振平台仿真建模

ADAMS是优秀的机械动力学分析软件，其ADAMS/view模块和ADAMS/vibration振动仿真分析模块应用较为广泛。在view模块里，对已完成的三维模型添加约束、材质等信息。其结果如图4所示。

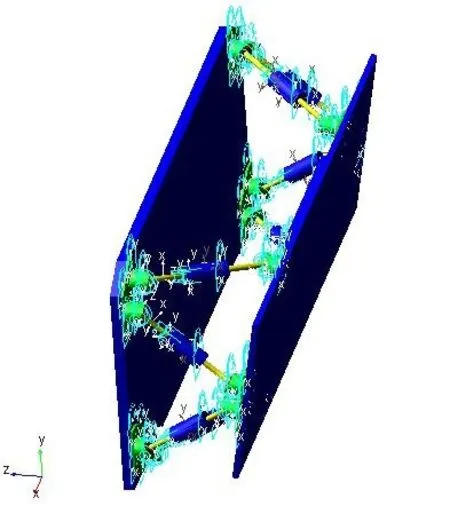
图4 三维仿真模型图

2.2 正弦扫频仿真

利用Adams/vibration模块对隔振平台进行受迫振动仿真，分析其隔振性能。在模拟飞机侧壁板的质心处建立6个输入、激励值为3 g正弦加速度激励输入通道；在模拟雷达板中间四点隔振杆连接处（建立四个marker点）和其质心处建立6个方向的输出通道。

设隔振系统的状态空间表达式为

其中：x为线性模型的状态矢量；

u=[Input_Channel_1,Input_Channel_2,Input_Channel_3,Input_Channel_4,Input_Channel_5,Input_Channel_6]T；

y= [Output_Channel_1,Output_Channel_2 ,Output_Channel_3, Output_Channel_4, Output_Channel_5,Output_Channe l_6]T；[A,B,C,D]为模型的状态矩阵，由ADAMS软件计算并定义。

拉普拉斯变换可得式（5）和式（6）。

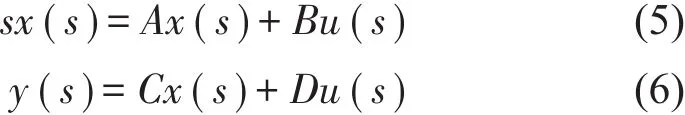
由式（5）和式（6）可以得到仿真模型在状态空间中的传递函数为

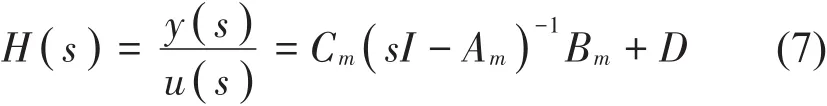
式（7）即为隔振平台的对应输入通道和输出通道的振动传递率函数。

频率-传递率曲线图结果，如图5所示。

2.3 半正弦冲击仿真

利用ADAMS/view模块，分析隔振平台缓冲性能。在模拟飞机侧壁板的质心处设置激励为16 g/11 ms的半正弦脉冲激励；在模拟雷达板的质心处和模拟雷达板中间四点隔振杆连接处（建立4个Marker点）测量其响应。仿真结果，如图6所示。

2.4 仿真结果分析

由曲线图5和图6，提取模拟雷达板质心处仿真峰值数据，可得表格1仿真数据。

由表1和图5、图6可知：①传递率峰值小于1.995倍，隔振平台侧壁多维隔振性能满足设计要求；②除Y移动方向的传递率峰值曲线响应一致性差外，X、Z方向均有较好的响应一致性；③受制于当前的实验仪器水平以及GJB150.16-2009喷气式飞机，只考察三个移动方向的隔振性能。

3 隔振平台实验研究

3.1 隔振平台振动实验

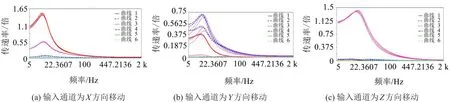
图5 扫频仿真传递率曲线图

定制实验隔振平台零部件，完成实验样机搭建。振动实验设备为某公司的DC系列通用型电动振动台，具体使用型号为DC-10000-100。振动实验三个方向，如图7所示。

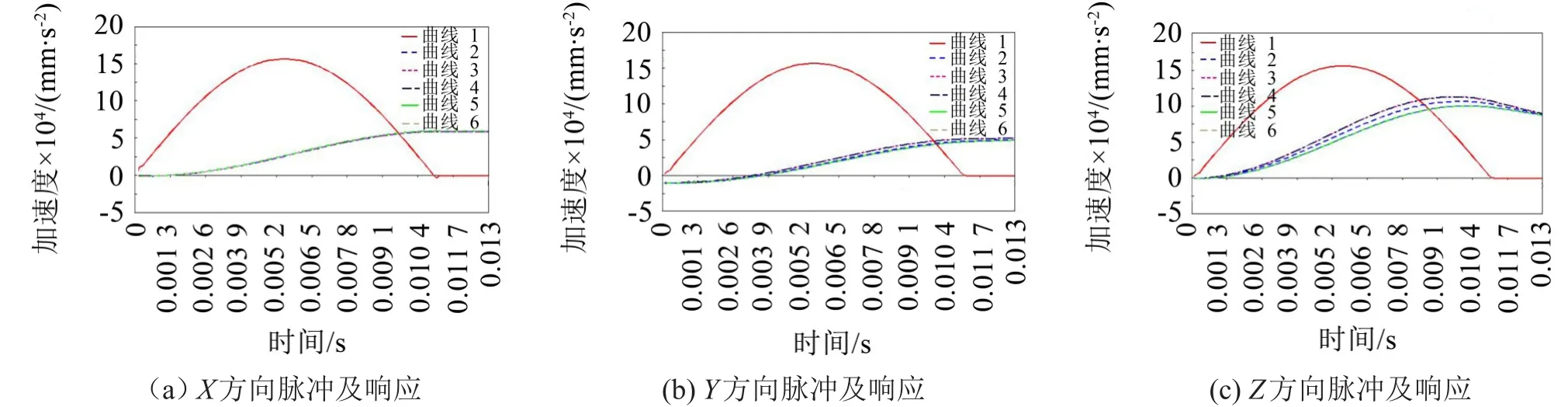
图6 冲击仿真响应曲线图

表1 振动仿真数据

图7 振动实验坐标轴指向

实验时，激励传感器贴在隔振杆输入端连接处附近，响应传感器贴合位置同仿真测量点。其扫频实验和冲击实验为按顺序同一个方向先后依次实验。扫频实验激励值如图8中B曲线所示，冲击实验激励值为16 g/11 ms的半正弦脉冲激励。

实验结果如图9所示，其中，扫频时，横坐标表示频率Hz。纵坐标表示重力加速度g；冲击时，横坐标表示时间ms，纵坐标表示重力加速度g。

3.2 隔振平台仿真和实验数据分析

通过对图9三个方向的振动实验数据处理，可以得出如表2所示实验数据。其中，传递率峰值为第一个峰值最值数据。

由表2和图9可知：

（1）三个方向振动实验除Y向扫频传递率峰值最大值大于1.995倍外，其余均满足隔振性能设计要求；

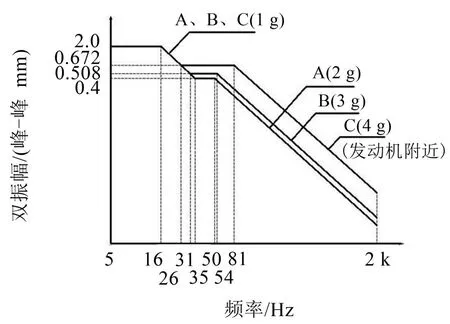
图8 功能振动试验曲线

（2）出现响应曲线不一致现象主要与定制双向隔振器刚度和阻尼的不完全一致有关；

（3）高频响应部分出现毛刺与高频模态有关。

4 结语

本文对侧壁式多维8杆并联被动隔振平台的隔振性能进行了三个移动方向隔振性能仿真和振动实验。

（1）从仿真结果角度，该仿真模型具有很好的隔振性能。

表2 振动实验数据结果

（2）除了Y向扫频实验传递率峰值最大值略大于1.995外，其余传递率峰值均小于1.995倍（6 dB）满足预期设计要求。说明该隔振平台具备较好的隔振性能，减少振动和冲击对侧壁式模拟雷达板的影响。

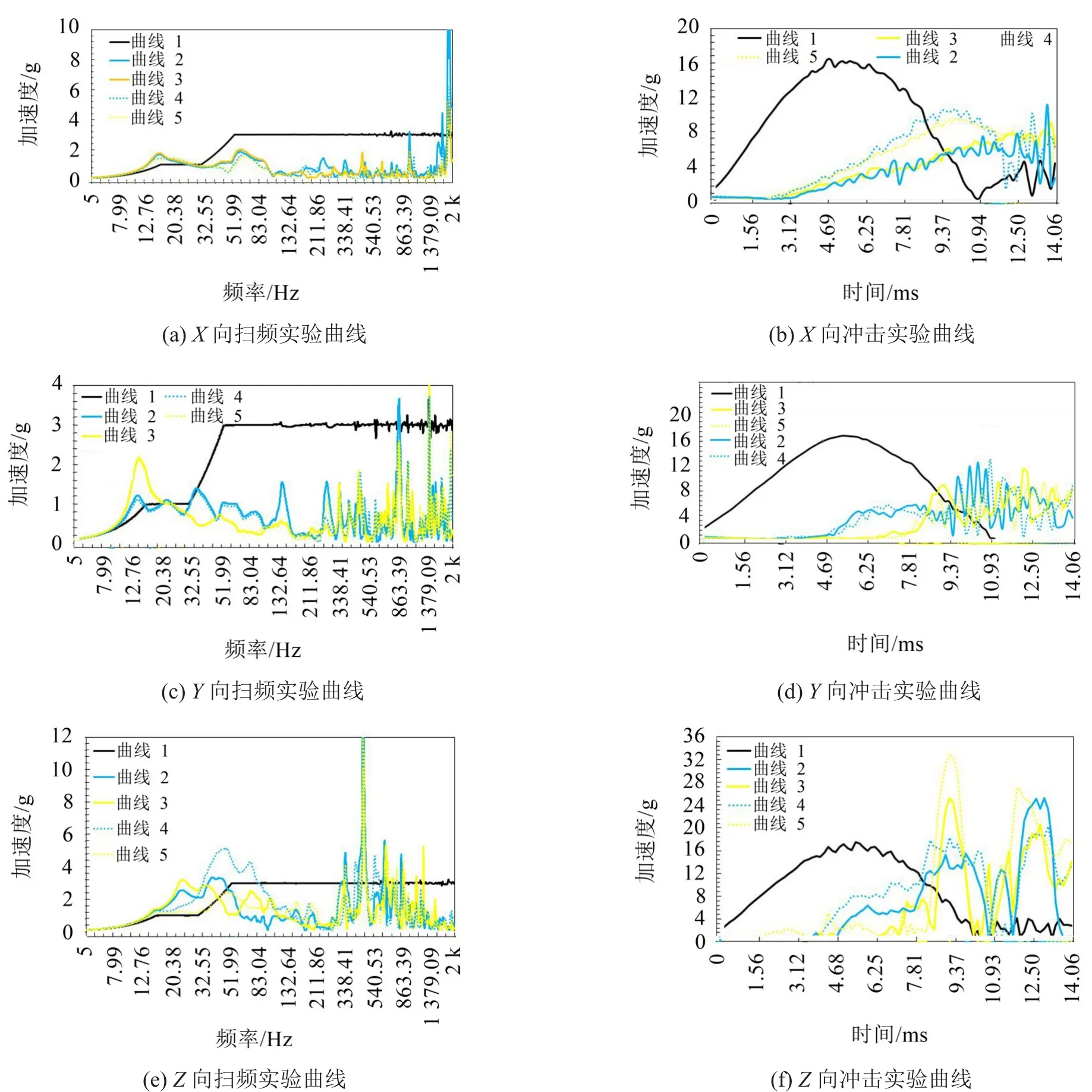
图9 扫频、冲击实验曲线

（3）由于振动实验只能测试三个移动方向的减振情况，对于三个转动方向的减振情况还有待于进一步研究。