矩形脉冲激励下悬挂减振系统易损件冲击特性
2018-10-23周园园陈安军
周园园,陈安军,2
(1.江南大学 机械工程学院,江苏 无锡 214122;2.国家轻工业包装制品质量监督检测中心,江苏 无锡 214122)
振动与冲击是产品运输过程中损伤的2个主要动力学因素,产品的包装结构设计对其防护具有重要的意义。悬挂系统通过上下8根弹簧将包装件悬吊于包装容器内,适用于低脆值精密仪器的减振防护[1]。针对单自由度悬挂系统,徐筱[2]研究了系统的跌落冲击响应特性,得到了产品的最大位移、最大加速度、冲击持续时间并分别与线性缓冲包装系统对比分析;王惠明等[3]以橡胶作为缓冲材料的悬挂系统为研究对象,建立系统非线性动力学方程,利用4阶龙格-库塔数值分析方法对方程求解,定量分析了系统参数对加速度和位移时间响应历程的影响;吴晓等[4–5]建立了悬挂系统的竖向振动控制方程,研究了系统竖向固有振动问题,讨论了悬挂系统的弹簧倾角、竖向振幅等对系统自振特性的影响,并建立了基础位移作用下该系统的非线性固有振动方程,采用L-P法推导出了系统固有振动的近似解,讨论了基础位移激励频率、激励振幅、悬挂弹簧倾角对系统固有振动特性的影响;王蕾等[6–10]建立了悬挂式弹簧缓冲包装系统的数学模型,讨论了相关参数对系统振动特性、冲击响应和跌落冲击响应的影响;宋爽等[11–15]以悬挂式弹簧缓冲系统作为研究对象,用变分迭代理论分析系统跌落冲击条件下的动力学特性及影响因素。现有悬挂系统的研究基于单自由度系统,李辉等[16]以考虑易损件悬挂系统为对象,建立2自由度系统动力学模型,但研究的是系统易损件跌落冲击特性,典型脉冲激励下系统易损件冲击特性及其影响因素的分析有待进一步拓展。
本文以考虑易损件2自由度悬挂系统为研究对象,建立矩形脉冲激励下系统无量纲动力学方程。利用4阶龙格-库塔数值分析方法对动力学方程进行求解,讨论系统悬挂角、频率比、主体与基础连接部阻尼比以及无量纲脉冲幅值等参数对易损件冲击响应特性的影响规律,进而为悬挂系统的设计提供理论参考。
1 动力学方程及其无量纲化
考虑易损件2自由度悬挂系统模型如图1所示,易损件和包装件主体的质量分别记为m1、m2,主体与易损件间阻尼系数记为c1,主体与基础连接部间阻尼系数记为c2,弹簧未变形时的原长及悬挂角分别记为l0和ϕ0,主体与易损件间连接刚度记为k1,8根悬挂弹簧的刚度记为k2。

图1 2自由度悬挂系统模型
以竖直向下为正,静平衡位置为坐标原点,参考文献[6–16],考虑易损件2自由度悬挂系统有阻尼动力学方程
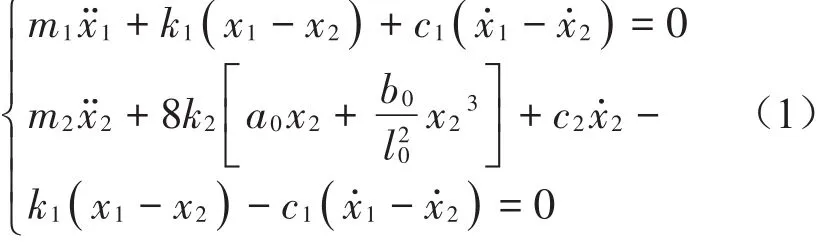
分别为易损件、主体速度;分别为易损件、主体加速度。
设系统受基础矩形脉冲激励,其数学表达式为
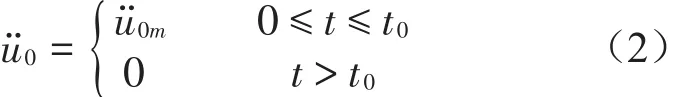
式中:t0为脉冲宽度,ü0m为脉冲幅值。该激励下系统冲击动力学方程为
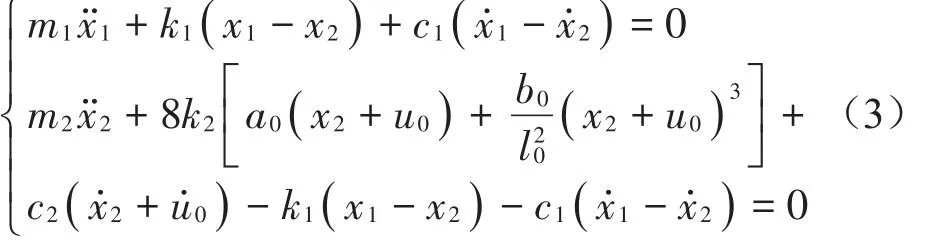
易损件及主体的初始条件分别为x1,2(0)=0,dx1,2(0)/dt=0。
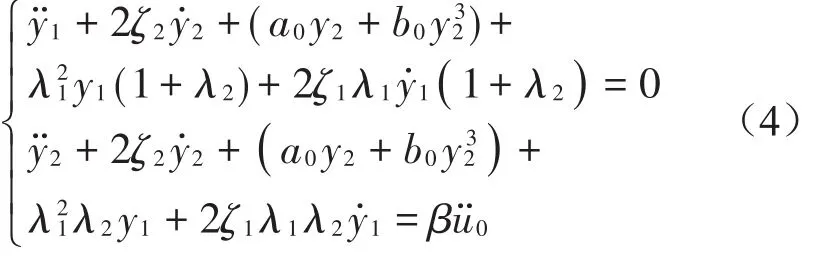
,分别为易损件、主体无量纲加速度。
初始条件变为:y1,2(0)=0,dy1,2(0)/dτ=0。
无量纲矩形脉冲激励数学表达式变为
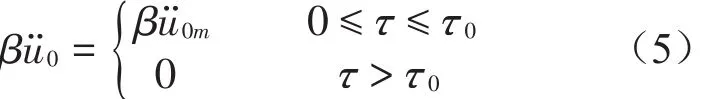
2 易损件位移响应
2.1 绝对位移响应
记易损件无量纲绝对位移为X1=y2-y1,取,不同系统悬挂角(ϕ0取60°,70°,80°,90°)易损件绝对位移响应如图 2(a)所示;取λ2=0.01,ϕ0=60°,ζ1=ζ2=0,βü0m=0.1,不同频率比(λ1取0.5,1,3,5,7)易损件绝对位移响应如图2(b)所示;取λ1=3,λ2=0.01,ϕ0=60°,ζ1=0,βü0m=0.1,不同阻尼比(ζ2取0.01,0.05,0.1,0.2)易损件绝对位移响应如图2(c)所示;取λ1=3,λ2=0.01,ϕ0=60°,ζ1=ζ2=0,不同无量纲脉冲幅值(βü0m取0.01,0.05,0.1,0.2)易损件绝对位移响应如图2(d)所示。
2.2 相对位移响应
记易损件无量纲相对位移为X2=y1,相关参数的选取同2.1,系统悬挂角、频率比、阻尼比、无量纲脉冲幅值对易损件相对位移的影响如图3所示。
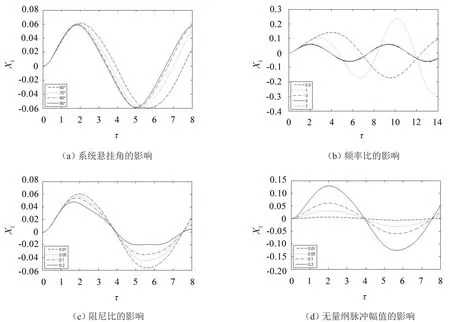
图2 易损件绝对位移响应
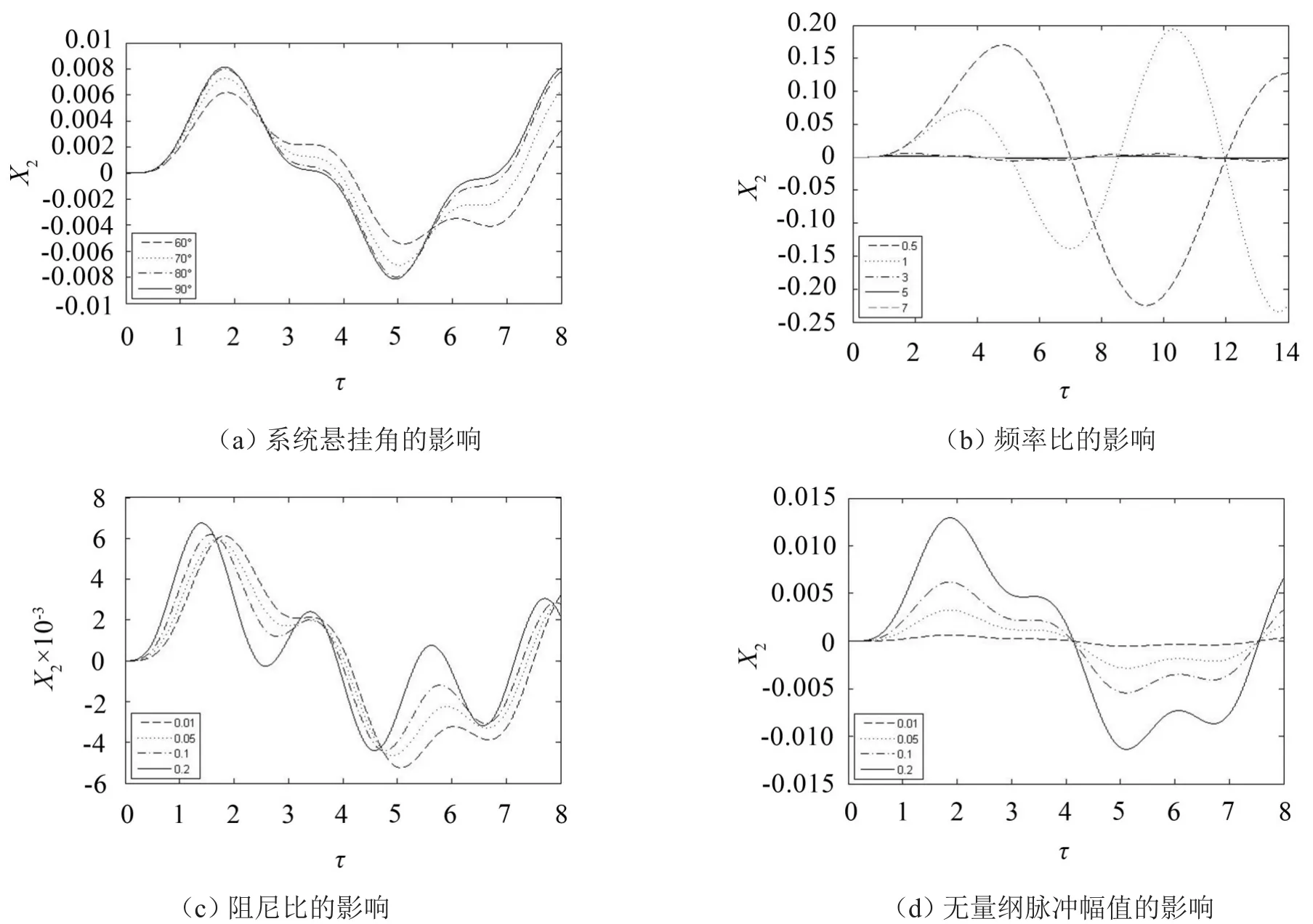
图3 易损件相对位移响应
3 易损件加速度响应
记易损件加速度为X3=ÿ2-ÿ1-βü0m,相关参数的选取同2.1,系统悬挂角、频率比、阻尼比、无量纲脉冲幅值对易损件相对位移的影响如图4所示。
4 易损件冲击响应影响因素分析
(1)系统悬挂角的影响。与线性系统(ϕ0=90°)相比,无阻尼条件下,随系统悬挂角的减小,易损件无量纲绝对位移幅值增加,相对位移幅值减少,加速度幅值减少,响应周期延长,其减振效果优于线性系统。
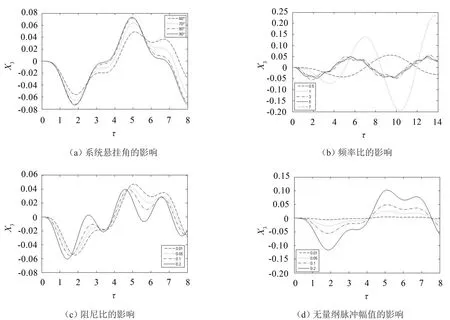
图4 易损件加速度响应
(2)频率比的影响。给定脉冲幅值、质量比及悬挂角条件下,无阻尼条件下,易损件位移及加速度响应对低频率比敏感,且当频率比λ1在1的附近时,易损件响应幅值变化显著,存在内共振现象。
(3)阻尼比的影响。矩形脉冲激励下,给定系统悬挂角、频率比以及质量比,易损件位移响应对主体与基础连接部阻尼比敏感,增加阻尼比可有效抑制易损件绝对位移响应幅值;随响应时间的增加,阻尼比抑制响应幅值效果更加明显。
(4)无量纲脉冲幅值的影响。无阻尼条件下,给定系统悬挂角、频率比以及质量比,易损件响应随无量纲脉冲幅值的增加而增加。
5 结语
在矩形脉冲激励作用下,考虑易损件2自由度悬挂系统冲击动力特性分析表明:易损件响应对频率比、主体与基础连接部阻尼比以及脉冲幅值较为敏感。较低频率比,易损件响应幅值变化显著,系统设计时选择较高频率比(建议λ1>5)能有效的降低响应幅值,提高系统抗冲击能力;增加基础与连接部阻尼比,能有效抑制易损件响应幅值;易损件响应随无量纲脉冲幅值的增加而增加,其幅值βü0m与系统特征参数β=T2/l0有关,可以通过改变悬挂弹簧长度l0获得较佳的减振效果。系统悬挂角ϕ0对易损件响应周期的影响较为显著,随悬挂角减少易损件响应周期延长,相对位移及加速度响应幅值减少,表现出较好的减振特性。
