货物批发价格关于包装成本的讨论
2018-10-23谷佳怡保定市第一中学
谷佳怡 保定市第一中学
我们从研究商品的批发价格着手,批发价格是这几种成本加商人的各种各样利润加价之和[1]。因为利润加价通常是用百分比表示额,本次讨论中把利润加价比例用常数表示,例如加价10%就以1.10乘常数表示。
计入批发价格中的主要成本是:生产该产品的成本:a;包装该产品的成本:b;运输该产品的成本:c;包装材料的成本:d;本文将在下面的模型中依次分别考虑这些成本。
有理由假设生产成本a与所生产的货物量成正比,记为a∝w,读作“a与重量w成正比”。
包装成本b取决于包装需要多长时间、封包要多长时间以及装箱备运要多长时间。第一部分时间大致与体积成比例,从而对于体积在一定范围内的包装,后两部分时间或许大抵相同。于是对于某些正的常数f和g,
运输成本c可能同时取决于重量和体积。因为体积与装满的包的重量成正比,所以c∝w。
包装用材料的成本d较为复杂。为了便于建立模型,我们假设d忽略不计。
根据以上分析,每件包装的成本取决于它的重量和体积。如果我们所考虑包装的变动范围不太大的话,有理由假设各种体积的包装所用的包装材料相同。所以每件包装所消耗的材料量与所覆盖的表面积成正比,取决于是摊平后运输还是成型后运输。所以包装品供应者为每件包装品所付的成本是都是常数,其中s是表面积。
现在由比例来论证[2]把一切都化为一个自变量—重量。假设各种包装品在几何形状上是大致相似的。体积几乎与线性尺度的立方成正比,表面积几乎与线性尺度的平方成正比:

于是,每千克的批发成本是:
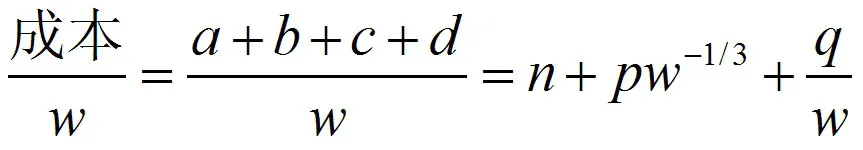
n,p,q为正数。因此看出,当包装增大时,每千克的成本下降。
因为每千克的成本价表达式中含有三个常数,所以对于一种产品,就得有多于三对的重量和成本的值。但是这是难以得到的,因为可用于某种产品的不同规格的包装只有有限几种。因此我们需要另一种不同的方法。每千克的成本下降速度为:
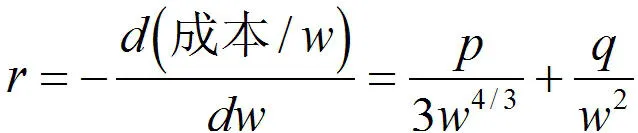
这是w的减函数。因此当包装比较大时,每千克的节省率增加的比较慢。我们也可以计算总节省率:
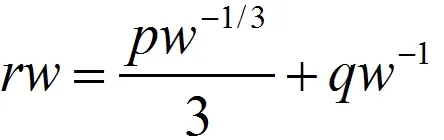
它也是w的减函数。
用户不见得了解这点,我们可用比较简单的措辞作类每千克的成本下降公式的说明:
购买预先包装好的产品时,把小型包装的包装规格增大一倍每千克所节省的价值,倾向于比大型的包装规格增大一倍所节省的价值高。
只要取,每千克的批发成本公式在w和2w的值之差,并验证这个差是w的减函数,便可以证明这点。我们说“倾向于”,是因为这个模型粗糙。
这次预测似乎在很大的程度上依赖于每千克的批发成本公式的精确形式,但实际上像这样的定性预测往往是很可靠的。如果我们对这个模型有更认真的要求,称心的还是从更一般的模型来推出这些预测,但是我不知道该怎么去做到这一点,并且觉得这问题也不值得去多费精力。
上面的讨论是关于批发价格的。关于零售价格又怎么样呢?零售商的成本取决于批发价、销售成本与仓库成本。同上面一样,后两种成本具有形式Hw+M。如果批发商把他的价格定位他的成本加一固定百分数,那么我们又得到形式如每千克的批发成本公式的方程,因而上面的得到的结论也适用于零售价格。
总的来说,我们讨论的问题与包装成本模型有关,由每千克的批发成本公式所得出的结论“大包装每千克的成本比较低”与本问题的真实结果不大一值,但是这只是一个粗略的模型,因为我们不能计算导数,只能算差分,所以我们不能检验方程每千克的成本下降速度公式。而且,将包装量加倍的法则也经常无法得到检验,因为制造商总是按各种各样的规格来包装产品。我们希望有一个形式上更加灵活的加倍法则。其实用有限差分[3]的方法可以得出“r是w的减函数”这一论断。
