M序列信号在主动声纳中的性能研究

吴一飞 李玉伟

（1.上海船舶电子设备研究所 上海 201108）（2.海军驻上海地区水声导航系统军事代表室 上海 201108）

1 引言

水下环境背景通常可以归分为两类：噪声限制背景、混响限制背景。在高斯白噪声限制背景下，对于任意的发射信号而言，获得最大信噪比的最佳检测器是匹配滤波器，并且可以通过加强发射信号的源级来有效地提高信噪比。而在浅海环境中，海底混响限制成为主要的背景，混响信号和发射信号之间存在较大的相似性，匹配滤波或者单方面地加强发射信号的声源级并不能有效地提高信混比。然而海底混响可以看作是海底静止目标的反射波在接收处的叠加，跟水下其他运动目标的反射波相比较，其回波频谱并没有发生频偏，所以在混响背景中对回波进行处理时需要对拷贝信号进行多组频率偏移，以此来达到对发生了频偏的目标回波部分完全匹配的目的，获得多普勒处理增益。但是并非所有的发射信号都适用于混响背景中探测水下运动目标，特别是诸如蛙人之类的慢速小目标，它们的目标强度弱、运动速度慢［10～11］，回波更加容易淹没在混响中，因此所选用的发射信号必须具有高敏感的多普勒特性（速度分辨力），同时还应兼具良好的距离分辨力。在主动声纳探测中常用的波形设计大体可以归为三大类［1］：CW信号、FM信号、伪随机（PN）信号［1］。其他形式的波形可认为是在这三类波形基础上的扩展。

CW脉冲的带宽B和周期T相互限制成反比例关系，长CW脉冲在具有良好的速度分辨力的同时却由于损失了带宽而导致时延分辨力较差［12］。在CW信号基础上设计的波形主要还包括SFM信号和Cox comb信号，这两种信号主要也是针对混响背景，通过拓展信号带宽来提高探测性能，但是时延分辨力并没有显著提高。FM信号的带宽和周期可以单独调节，因而对于相同的速度分辨力，却有着比CW信号优良的时延分辨力，此类信号主要有LFM信号和HFM信号，但是这两种信号的多普勒容限高，对微小的速度变化并不敏感。文中主要选择第三类伪随机信号进行分析，通过具有伪随机性的M序列对CW信号进行编码，在保证其多普勒敏感特性的同时拓宽频带，使其同时兼具优越的速度-时延分辨力［8～9］。

2 M序列信号设计和抗混响能力分析

2.1 M序列信号产生机理及特性分析

伪随机序列（Pseudo Noise，PN）是一个1和0的码序列，它的自相关函数具有与白噪声自相关函数相似的性质，到目前为止，最为大家熟知的二进制PN码序列是最大长度移位寄存器序列，即M序列。一个M序列的长度为P=2m-1，可由一个m级的带有线性反馈的移位寄存器产生。这个序列是周期的，周期为P。每个周期内有2m-1个1和2m-1-1个0的序列［2］。文章将｛0，1｝的二进制M序列映射为｛1，-1｝的相应序列来对CW信号进行相位直扩。

假设某一M序列每个码元宽度为τ，则第k个码元编码CW信号的时域表达式可以写成［2］：

式中，fc为CW信号的中心频率，ψ为信号的初始相位。编码后信号的带宽B与子脉冲带宽相近：B=1/τ。

图1分析了M序列的多普勒敏感性。其中码元宽度τ=0.1ms，信号中心频率fc=60kHz，-3dB处信号带宽为10kHz；取码长为P=1023，则编码持续时间为T=102.3ms，相应的频偏df=1/T=9.8Hz。当回波由于目标运动引起频偏超过df时，回波信号和发射信号相关性下降。图中分别选取了相对速度v=｛0，0.1，0.15，0.5｝m/s的四组回波信号与发射信号进行互相关处理，图中可见随着相对速度的增大，发射信号与回波之间的互相关程度降低。

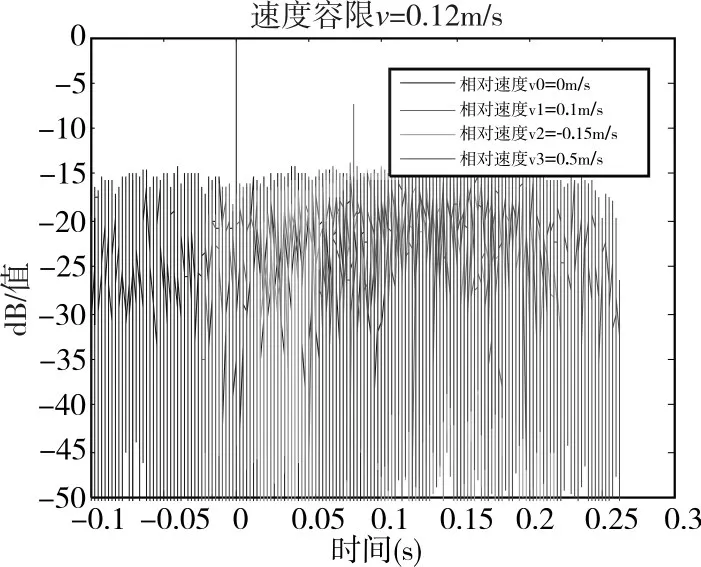
图1 M序列信号多普勒敏感性分析

2.2 抗混响能力参考指标

为了统一比较不同的发射波形的探测性能，本文采用模糊图结合Q函数的分析方法。模糊图是信号回波和拷贝信号组的关于时延和速度的整体输出，反映了目标距离和速度的分辨能力。根据研究目的的不同，可将其分为自模糊图和互模糊图函数。其中自模糊图反映了单个信号周期内回波与其同周期内拷贝信号的匹配效果。函数表达式为［1］

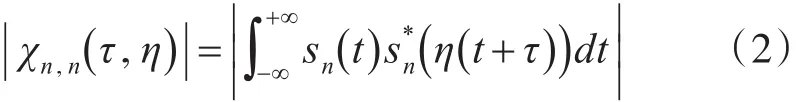
式中，sn(t)为第n个周期内的发射信号，(η (t +τ)) 为回波信号的共轭，τ为时延，η为多普勒伸缩因子，在数学上相当于对信号进行重采样，定义：

式中，v为目标相对于声纳平台的径向速度，c为水中声速。

对自模糊度图的物理意义进一步扩展来描述单个周期信号与不同周期内拷贝信号的匹配效果，即为互模糊图。函数定义为［1］

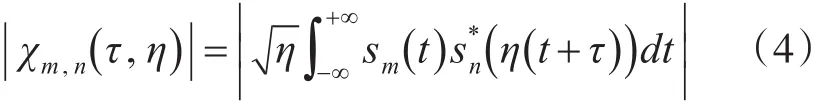
我们希望同一周期内信号自相关性尽量高，不同周期外信号互相关性尽量低。混响限制背景下考察某一波形检测能力的另外一个指标是Q函数，Q函数定义为［1］

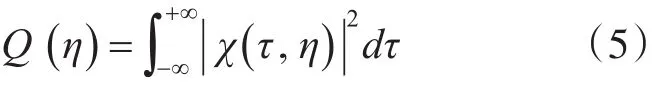
由上式可知Q函数可以理解为信号的模糊函数在某个频率点的横截面上的模平方在时间轴上的积分，由此可近似为混响在该点上的能量分布［4］。所以，当频点（速度点）上的Q值越小，说明该点聚集的能量越弱。

图2、图3给出了CW信号、LFM信号、M序列编码CW信号的自模糊度和Q函数对比图。由图2可见M序列编码CW信号的-3dB模糊图的时间宽度约为0.6τ=0.06ms，速度宽度约为0.12m/s，与理论值相符。相对未编码之前的CW而言，由于信号频谱的扩宽，使得匹配能量在带宽范围内得到平均而下降［3］，下降的能量级为

ΔD=10·lg（P）=30.1dB（图 3（a））。

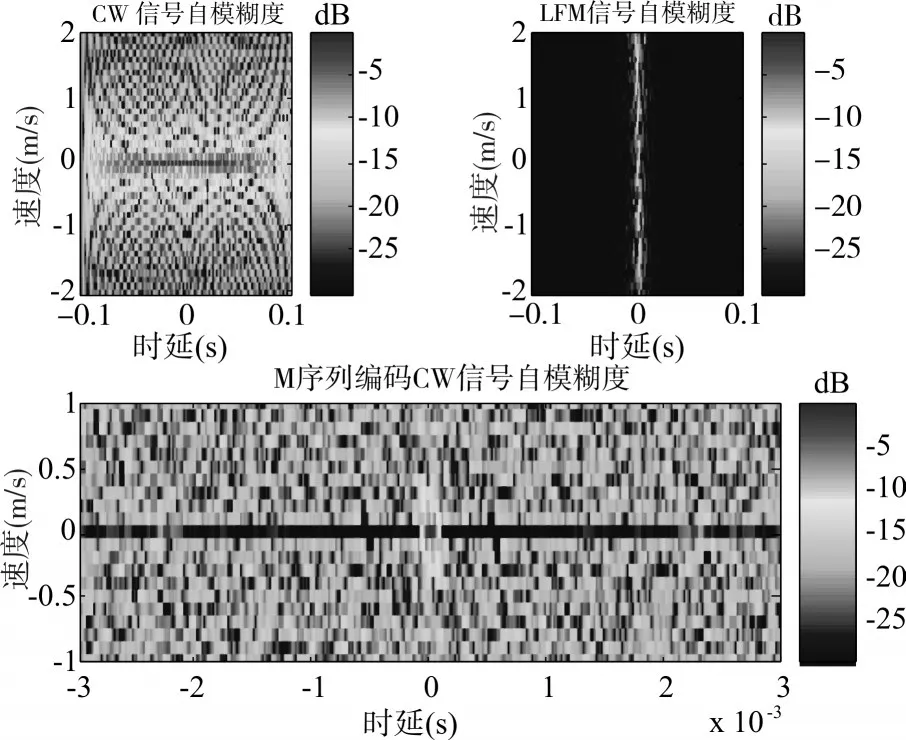
图2三类信号模糊图分析

图3 （b）中给出了M序列信号加窗前后的对比分析。加上128阶的汉明窗虽然可以有效地压制信号的旁瓣，但是对于能量聚集的宽度并没有明显的改变，这是因为加窗只是改变信号的边缘特性，并没有影响子码宽度以及信号长度。

3 Matlab仿真实验设计及结果分析

本次仿真实验中首先根据文献［5］～［7］中提出的方法建立海底混响模型。考虑海底为淤泥砂砾混合物质，海底反射强度取海试经验值S=-27dB；海深H=20m，发射、接收换能器之间距离L=1m，置于海深h=10m处；设想一个等效的理想指向性图案，声纳方位角束宽为pi/6，开角内有均匀的单位响应，在此开角外响应为零；以开始发射信号的时刻为时间轴原点。步骤设置如下：

Step1：P=1023，τ=0.1ms，Tsig=102.3ms。发射信号中心频率fc=60kHz，混响信号时域波形、幅频曲线分别如图4（a）、4（b）所示。可见每发射单个脉冲信号，混响持续时间约为0.8s。混响信号的频谱特性与发射信号相似。

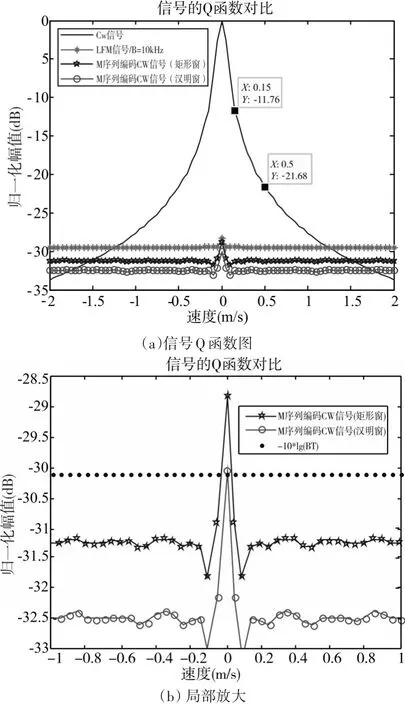
图3 M序列信号Q函数分析

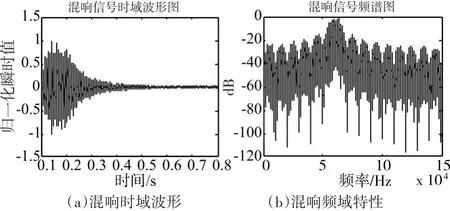
图4 M序列信号混响时频域特性

Step2：信号脉冲重复发射周期TPAS=1s，重复发射20次。水下目标参数及其他如下：

目标1：TS1=-20dB，距离声纳平台R1=90m，以v1=0.15m/s的速度靠近声纳平台。

目标2：TS2=-20dB，距离声纳平台R2=300m，以v2=-0.5m/s的速度远离声纳平台。

Step3：不考虑直达声的影响，忽略背景噪声，在0.1s之后开始采集数据，回波信号时域波形如图5所示。

Step4：采用CW信号、LFM信号、M序列编码CW信号三种波形重复step2、step3。

Step5：对以上三种回波各自进行互模糊度和Q函数分析。其中CW信号如图6（a）、6（b）；LFM信号如图6（c）、6（d）；M序列信号如图6（e）、6（f）所示：

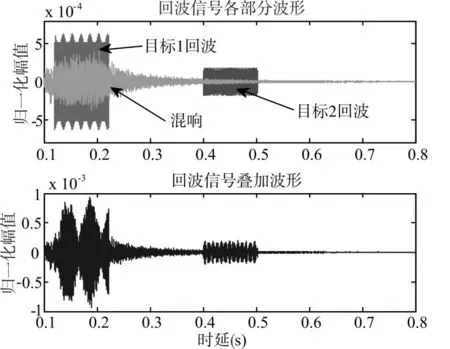
图5 回波信号时域波形

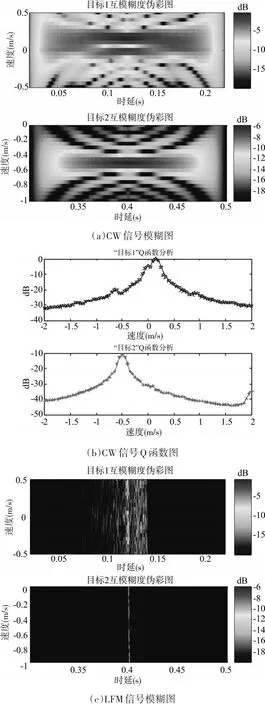
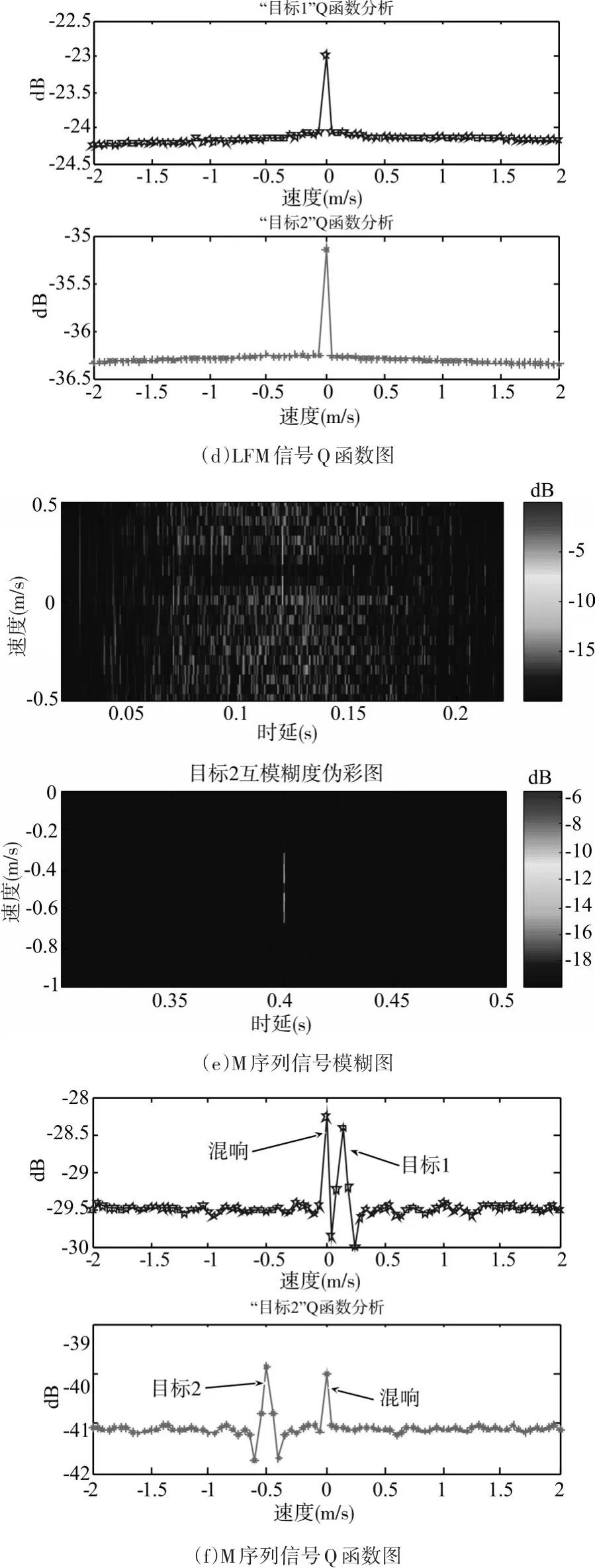
图8 回波信号处理结果

为了方便对比，图6（b）、6（d）、6（f）分别以图6（b）中峰值为参考进行了能量归一化。

对CW信号而言，由于混响带较宽，目标1在零多普勒区域附近微小的速度变化并没有跳出混响带，混响对回波的干扰比较严重。由图3（a）可知，相对于速度v1=0.15m/s处，在速度v2=0.5m/s处混响能量下降约10dB，探测效果较好。但是无论是目标1或者目标2，图6（a）中的时延测量精度都差。

对LFM信号而言，尽管多普勒容限较高导致速度分辨力较差，但是10kHz的带宽对应的时延分辨力为0.1ms，时延测量精度得到保证。

对M序列编码的CW信号而言，0.1ms的时延分辨力和0.12m/s的速度分辨力使其同时兼备CW信号和LFM信号的优点，如图6（e）、6（f）所示，可以看到能量在目标1、目标2的速度处得到良好的聚集。

4 结语

在复杂多变的浅海信道中，海底混响干扰一直是主动声纳探测过程中的一大难题。与发射信号的极大相似性使得在接收信号中难以分离出目标回波和混响信号。文章从模糊度函数以及Q函数的物理意义出发，采用最长伪随机噪声序列M序列对一般的CW信号进行编码，利用目标运动产生的多普勒频偏来对拷贝信号进行匹配，该信号敏感的多普勒特性使其获得较高的处理增益。与传统的CW信号以及LFM信号的比较表明，M序列信号具有更优的速度—时延分辨力，并且通过设计实验仿真得到验证，该信号可应用于混响限制背景中对慢速目标的探测。