试验海区水文参数时间序列的多周期重构预测方法

艾锐峰 程 杰 欧阳军 孙云鹏

（解放军63850部队 白城 137001）

1 引言

在进行海上装备试验时，需要提前掌握海区水文要素（水温、盐度、海面风场、海流、波浪等）的变化规律，从而为试验方案的制定提供决策依据。动力学的气象海洋预报可以提供一定程度的参考［1］，但对部分水文参数（如海水温度）能力有限。目前的处理手段是通过历史数据的统计处理，提供海区水文参数不同时间周期上（年、月、日等）的平均值、方差、最大最小值等统计量作为未来值的估计。由于水文参数影响因素众多、变化机理复杂、空变时变特性，此类估计量作为预测值相对粗糙。

更进一步的分析方法有回归分析、马尔可夫概型分析和时间序列分析等［2］。回归分析通过变量和因变量样本数据的拟合，建立回归模型，利用模型对未来时刻值作预报估计。回归分析需要变量、因变量之间确实存在物理上的关联关系，且需要二者的同步样本值，若只有本要素的时间测量序列，则无法进行回归分析［3］。马尔可夫概型分析以时间序列内部概率分布结构为基础，建立马尔可夫链，通过待分析参数状态的逐步转移，实现对参数时间演变过程的分析与预测［4］。它要求参数序列满足无后效特点，适用场合有限［5］。基于ARIMA模型的时间序列分析方法是一种适用性更好的方法，它只基于待分析参数的历史时间序列数据，建立参数化的模型，实现对未来时刻值的递推预测［6～7］。

一种水文要素受到多种不同效力因素的影响，其最终呈现的时间序列吸收了所有影响因素的作用效应，从而导致其可能是非平稳的时间序列。当利用ARIMA模型分析法进行建模与预测时，虽然通过差分方法可以进行序列的平稳化预处理，但当平稳化程度有限时预测效果下降［8～9］。分析时间序列的影响因子，当单一因子作用时，产生的影响相对确定，且不同的影响因子可以认为作用于不同的尺度上。鉴于此，本文运用小波变换与ARIMA模型分析法，通过时间序列的多周期拆分、建模预测、反向组合的方式，设计了一种基于多周期重构的预测方法。利用海洋浮标测量数据对该方法与传统的ARIMA方法进行对照分析。

2 信号的多尺度分解与ARIMA建模

2.1 基于小波变换的信号多尺度分解原理

对水文参数时间序列的多周期拆分基于小波分析［10］。小波变换通过逐渐精细的取样步长聚焦到信号的细节，从而在时域和频域同时具有良好的局部化性质。它相当于通过不同尺度参数的选择将信号分解到对应的尺度空间上去［11］。

设 f(t)为空间L2(R)上的信号函数，则其小波变换为

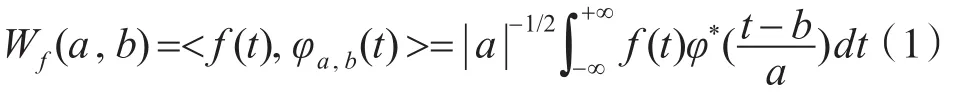
式 （1） 中 φ(t) 为 母 小 波 函 数 ，φa,b(t)= ||a-1/2φ((t-b)/a)是 φ(t)经过伸缩平移变换得到的一系列基函数。其中a为尺度参数（或者伸缩参数），b为平移参数。通过小波逆变换可以重构原信号函数，如式（2）所示：

基于小波变换可以实现对信号的多尺度分解。设{φ (t)j,k}j,k∈Z是正交小波基函数，对应于L2(R)空间的分解。其中，Z为整数。则可以将 f(t)展开为

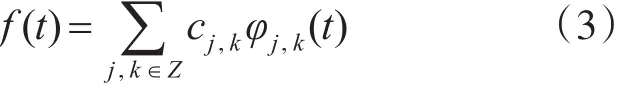
式（3）中 cj,k=＜f(t),φj,k(t)＞ 为小波级数。令，则 fj(t)为信号 f(t)在子空间Vj上的投影。于是可以如图1所示，将信号分解到不同的尺度空间上去。

图1 信号的小波分解示意图

2.2 时间序列的ARIMA建模方法

自回归积分滑动平均模型（Autoregressive Integrated Moving Average Model，ARIMA）分析法是一种利用参数模型对随机分布信号序列进行处理，从而估计出模型参数、建立递推模型、进行数据序列的拟合与预测的方法［6］。其一般步骤：通过差分将非平稳时间序列转换为平稳序列，再经过模型类型识别、模型定阶、模型参数估计建立ARMA模型，然后利用ARMA模型进行历史数据序列的拟合或者对未来值进行递推预测。

设某时间序列为 fn，n=1,2,…,N。若其非平稳，则对其通过差分实现平稳化处理，即令

f′n=fn-fn-1。其 ARMA(P,Q)模型为式（4）所示：

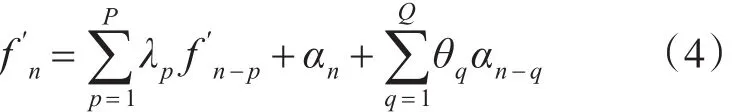
其中，模型参数 λp、θq和白噪声序列 αn的方差为待估计项。通过对序列进行相关性分析［7，8］，判断适用的模型为AR、MA还是ARMA。模型阶次(P,Q)的确定采用AIC准则［8］。模型参数 λp、θq可通过最小二乘法解算得到［9］。

利用建立的ARMA(P,Q)模型可以实现对未来数据的递推预测。设(P,Q)=(2,3)，利用预测。以k=1步预测为例，如式（5）所示，进行递推求解：

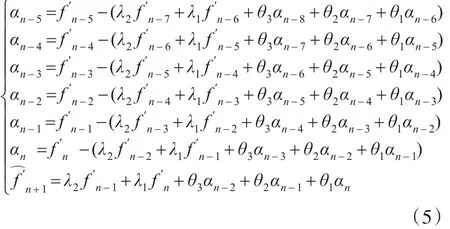
3 时间序列的多周期重构预测方法

3.1 时间序列的多周期重构预测模型

以海面气温或水温为例，设 fn=tn，温度受季节因素影响，温度时间序列tn呈现季节变化的特征。一日当中昼夜太阳辐射变化，温度时间序列tn呈现日变化的特征。同时温度还受到其他各种因素影响［12］。所有这些因素共同作用导致所测量的温度时间序列tn呈现随机性和规律性并存的局面。ARMA模型分析方法可以实现对时间序列的参数化建模，并对未来值进行递推预测。在理论上，当序列是平稳随机序列时，ARMA方法的性能较好；当序列非平稳时，虽然可以通过差分，趋势项剔除的方法对原序列进行平稳化处理，但是平稳化处理后的序列也并非完全平稳。从物理机理上理解，假设tn只受季节变化的影响，则测量值tn为平稳的周期序列，变化周期与季节变化同步；假设tn只受昼夜变化的影响，则tn为平稳的周期序列，变化周期与昼夜变化同步。以此类推，可以假设tn受到m=1,2,…,M个因素影响，单个因素产生的序列ζm,n可以认为是平稳序列，于是所观测的序列tn可以用式（6）表示：

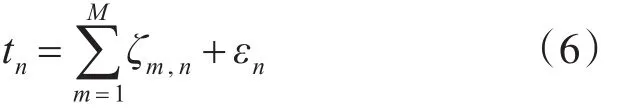
其中εn为剩余其他因素产生的序列。

一般而言，M个影响因素拥有不同的作用时间尺度。基于此假定，设有时间序列xn，n=1,2,…,N，构建如下的时间序列多周期重构预测模型，以实现利用序列xn预测xn+k。

首先令 xn=xm,n，其中m=1,2,…,M 为分解的次数。利用小波变换对xm,n进行分解，得到序列xm,n的细节部分[vm,1,n,vm,2,n,…vm,L,n]和概貌部分sm,n；剔除细节部分，取sm,n作周期为Tm的滑动平均，得到 ym,n；基于ARIMA方法，利用 ym,n建立模型 ARIMA(p,I,q)，利用 ARIMA(p,I,q)递推预测yˆm,n+k。同时，令 zm,n=xm,n-ym,n，对差序列 zm,n做下一步的分解，即令m=m+1，循环操作。最后将分解后的预测序列组合起来重构为最终的预测序列 xˆn+k。

图2 时间序列多周期重构预测模型

3.2 具体的预测方法

下面为具体的预测方法：

令m=1,2,…,M，即共进行M重分解预测操作。

1）取历史数据序列 xn，令 xn=xm,n，m=1，作第一个周期的分解预测操作。首先，运用2.1节的方法，对xm,n进行小波分解，小波分解层数设为L。由分解得到的小波系数[cD1,cD2,…cDL,cA]逆变换得到序列 xm,n的细节部分[vm,1,n,vm,2,n,…vm,L,n]和概貌部分sm,n。

2）剔除细节部分，取sm,n作周期为Tm的滑动平均，得到 ym,n，即

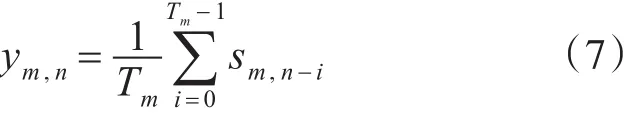
做差序列zm,n=xm,n-ym,n，从而将原序列xm,n分解为主序列 ym,n和差序列zm,n。

3）令 m=m+1，对差序列 zm,n重新进行1）、2）的操作，进行进一步的分解。经过M重分解后，可以将原序列 xn=x1,n分解为 y1,n,y2,n,…,yM,n,zM,n。即式（8）、（9）所示：

4）运用2.2节的方法，对 y1,n,y2,n,…,yM,n,zM,n分别进行ARIMA建模，利用建立的模型ARIMA(p,I,q)分别进行k步递推预测 yˆm,n+k。

5）将预测值组合起来，实现对xn+k的预测，即

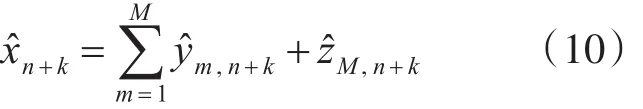
4 数据分析

利用实际数据序列，将所构建的时间序列多周期重构预测方法（下面简称为MTC方法）与直接的ARIMA方法的预测性能进行比较。

按照3.2节的处理步骤，对某海洋浮标站的海面气温测量数据进行分析。浮标站所处位置为（123°E，38°N）。数据采集时间区间为2010年7月28日至2012年7月27日，采样间隔为每小时一次，共计12100个数据。如图3所示，将温度时间序列分为两部分，前20%作为样本进行模型构建，后80%作为模型递推预测效果的比对。

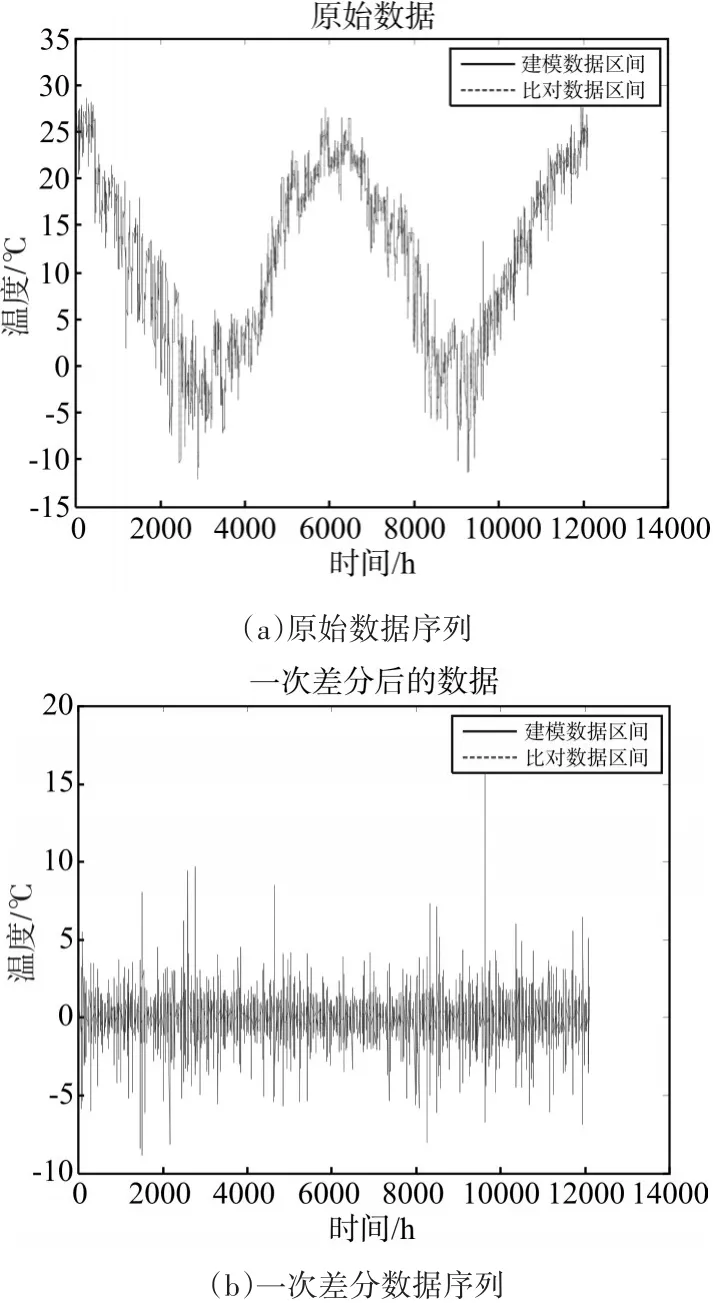
图3 海洋浮标温度测量数据

差分操作可以对数据序列进行平稳化处理，图3（b）为温度数据序列一次差分后的结果。根据MTC方法的处理流程，对温度时间序列进行三重分解即 M=3，滑动平均周期分别为T1=720（月）、T2=168（周）、T1=24（日）。原始序列被分解为X1=Y1+Y2+Y3+Z3。

图4为温度时间序列第一重分解。其中X1为原始数据序列，S1为X1经小波变换剔除细节部分后的序列，将之以周期T1=720滑动平均后的序列为Y1，Z1为X1减去Y1后的差序列。

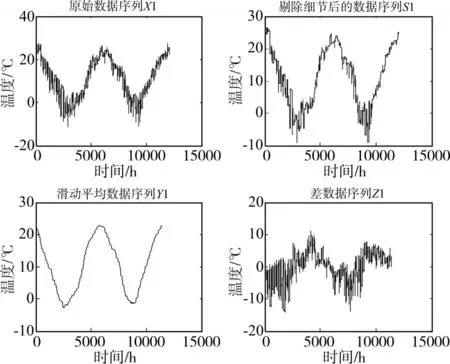
图4 温度时间序列第一重分解

图5 为将第一重分解后的差序列Z1（即X2）继续分解后的处理结果。

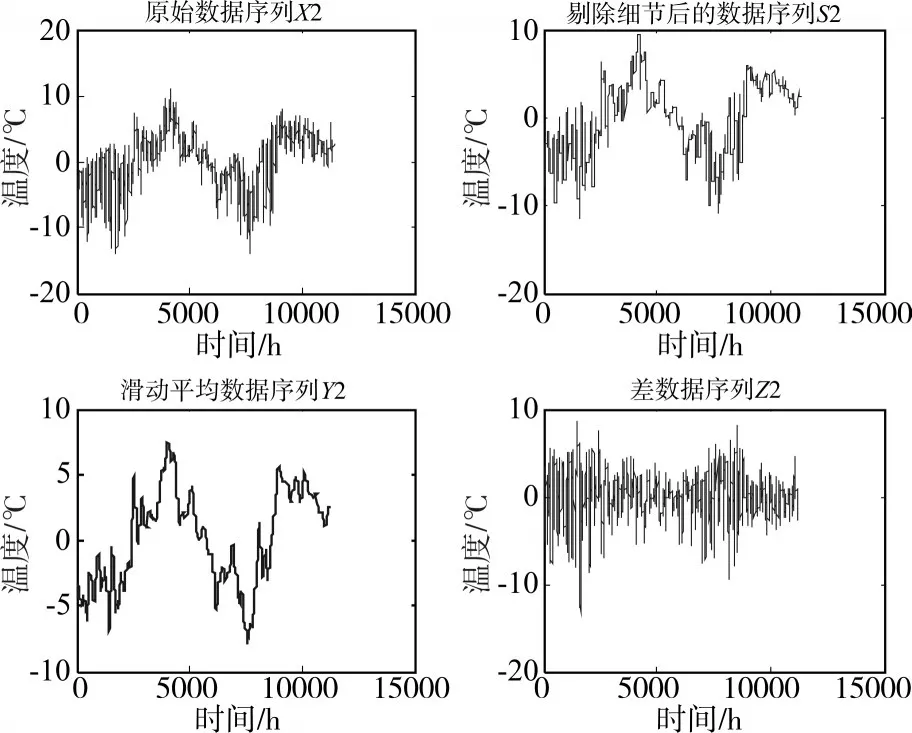
图5 温度时间序列第二重分解

图6 为将第二重分解后的差序列Z2（即X3）继续分解后的处理结果。

根据上面的多周期拆分、再逐一建模递推预测、再反向组合，得到图7（a）的一步递推预测结果，将之与直接ARIMA方法预测结果进行比较。

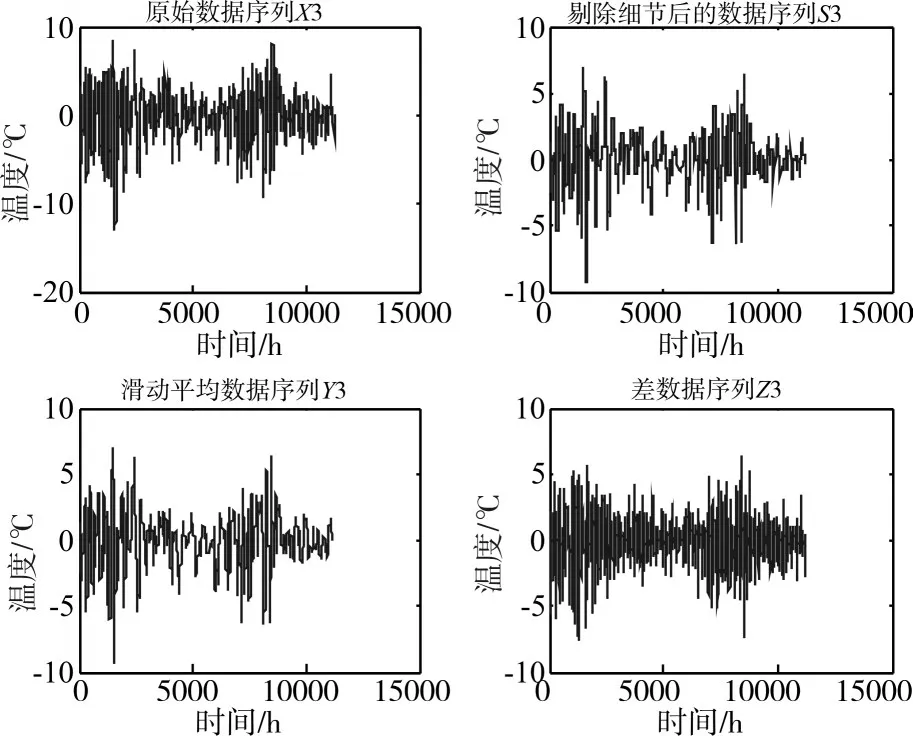
图6 温度时间序列第三重分解

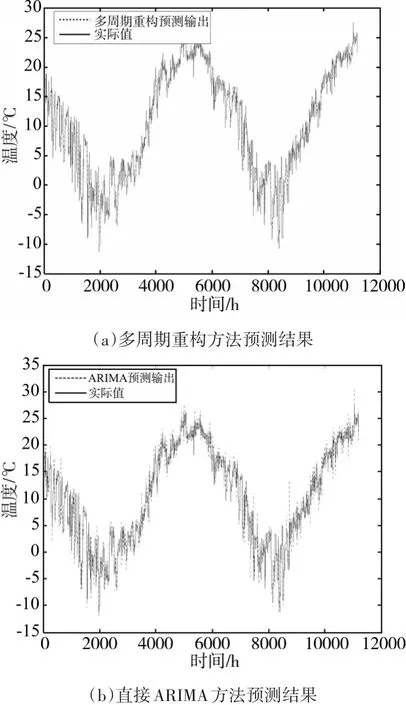
图7 一步递推预测结果

图8 为两种方法的预测误差比较，直接ARIMA方法预测误差的标准差为1.6℃，多周期重构方法预测误差的标准差为0.72℃，性能得到提升。

图8 一步递推预测结果的误差

5 结语

本文通过时间序列影响因子的分析，假定最终的时间序列由一个个单一因子作用下的序列组合而成，且各因子作用于不同的时间尺度。基于此假设，运用小波变换和滑动平均计算对原始序列进行若干周期的层层分解；再运用ARIMA建模方法对分解后的序列分别进行ARIMA模型构建与递推预测，通过预测结果的反向重构实现对原始序列未来值的预测，从而构建了一种时间序列预测的新方法。

实际时间序列数据的建模与预测结果表明，此方法相比直接的ARIMA方法，预测准确度有一定程度的提升。可对试验海区水文参数序列变换采样率，利用此模型对历史数据进行分析，获取海区水文参数的规律及未来时刻的预测值，为试验决策提供参考。另外，在程序计算中发现，分解周期及次数的选择、小波变换分层数的选择均对该方法的预测效果有影响，需要在后续工作中进行深入的分析，研究其与实际水文参数影响因素及作用机理的关联关系，形成相匹配的预测模型；其次，多步预测的效果也有待研究。