包装箱正压环境下航天器总漏率检测技术
2018-10-23杨定魁崔寓淏孟冬辉喻新发马永强
窦 威,杨定魁,崔寓淏,孟冬辉,喻新发,马永强
(北京卫星环境工程研究所,北京 100094)
0 引言
氦质谱非真空累积检漏方法采用密封的航天器包装箱作为示漏氦气收集容器,对被测航天器子系统充入工作压力的高纯氦气,并封入包装箱,通过检漏仪测试包装箱中氦气体积分数的累积变化得到被测航天器子系统的总漏率。
现阶段,该技术是在常压环境下开始累积,在累积过程中,航天器包装箱内、外压力差会受箱体内、外温度和大气压变化影响,可能出现包装箱处于正压或负压的工况。基于此,航天器包装箱需进行结构加强设计,而承载负压的设计会造成航天器包装箱质量的大幅增加。
本文研究在正压环境下利用氦质谱非真空累积检漏方法进行航天器总漏率测试的可行性和测试结果的准确性,判断这一新的检漏方法是否满足航天器总漏率检测的需求,进而为航天器包装箱的减重设计和利用正压环境进行检漏测试的可行性提供参考。
1 工程现状与研究目标
1.1 常压环境下总漏率检测
目前,通常利用航天器包装箱进行示漏气体累积收集,采用氦质谱技术进行常压环境下总漏率检测[1],系统原理如图1所示。
总漏率检测方法如下:
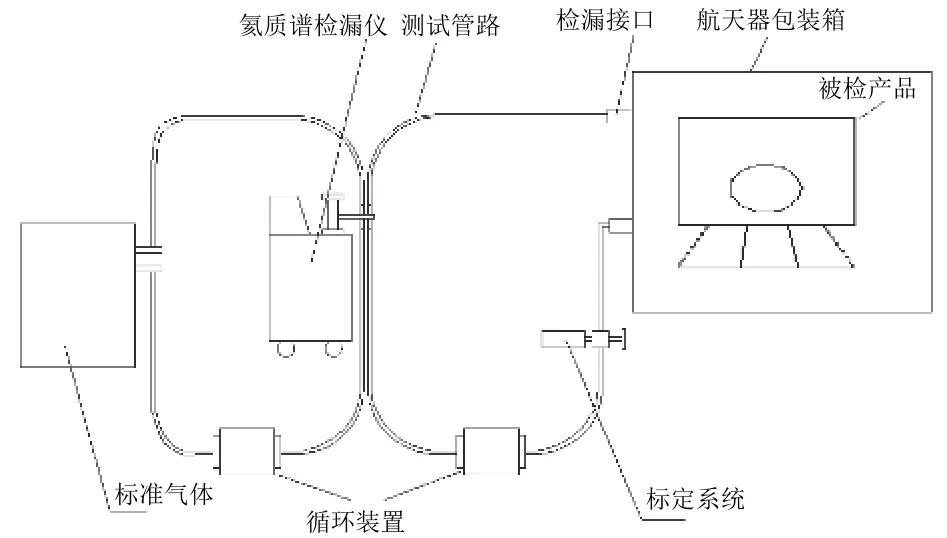
图1 常压环境下航天器总漏率检测系统原理示意Fig. 1 Principle of the total leakage rate testing of spacecraft under ordinary pressure environment
1)以工作压力的氦气作为示漏气体充入航天器子系统中并放入密闭包装箱内;利用包装箱内的风机使其内部气体混合均匀,以标准气体的氦体积分数作为基准值,用检漏仪测量包装箱内的氦体积分数本底值,记为测量初值u1,记录测量时间t1。
2)保持航天器包装箱密封,如果被检系统有泄漏,则包装箱内的氦气体积分数会升高,为测得箱内氦体积分数变化量,需要累积一定时间t(一般为24 h)。
3)通过风机搅拌使包装箱内的气体混合均匀,用与步骤1)相同的测试方法测量包装箱内的氦体积分数,记为终值u2,记录测量时间t2。
4)终值测量结束后,将一定量w(w=PV,即一定体积、一定压力)的氦气放入包装箱中进行标定[2],通过风机搅拌使箱内气体混合均匀后用相同测试方法测量此时包装箱内的氦体积分数,记为样值,记录测量时间。
5)计算被检件的总漏率

在总漏率检测过程中,环境温度变化量很小,在±2 ℃范围内;同时,整个检漏过程中,外界大气压是波动的,24 h内最大值和最小值之差可达3000 Pa。综合温度变化与外界大气压变化,随着检漏累积时间的增长,包装箱内外会产生正或负的压差,根据以往经验,包装箱内外压差的最大量值约为2000 Pa。
1.2 研究目标
为避免出现包装箱负压工况使航天器包装箱在设计时不得不加强结构强度而导致箱体重量过大,改进现有常压总漏率检测方法,在航天器放入包装箱并完成密封后向箱内充入2000 Pa的高纯氮气,创造正压环境,之后再进行初值、终值和样值的测量,这样,在24 h累积的过程中,即使外部大气压不断变化,包装箱内相对外部始终处于正压状态。
由于航天器被检系统多种多样,总漏率要求也各不相同,分布量级较广,我们选取典型漏率量级1×10-4Pa·m3/s进行研究。按照检漏相关标准,检测系统的灵敏度需要优于产品设计指标1个数量级。因此,针对包装箱正压环境下航天器总漏率检漏技术的研究,需以通过校准的漏率为1×10-5Pa·m3/s左右的标准漏孔作为研究和被测对象。通过理论分析研究和试验测试,拟达到以下研究目标:
1)理论分析正压环境下氦质谱总漏率检测技术的可行性(以误差不大于5%作为理论分析边界条件);
2)建立试验系统,对正压和常压环境下氦质谱总漏率检测的结果进行对比,判断2种方法对于校准量值为1×10-5Pa·m3/s左右标准漏孔的实测值偏差是否在±20%以内,以验证正压环境下的总漏率检测方法是否可行。
2 理论分析
包装箱正压环境下进行的航天器总漏率检测方法,相对常压环境检测方法,主要区别为包装箱内初始就存在高于外部2000 Pa的压力,会造成以下影响[4]:
1)包装箱内原有气体和航天器泄漏至箱内的示漏气体存在随压差泄漏出包装箱外的可能[5],从而对测量结果造成影响,因此必须从理论上分析包装箱本体密封性与航天器总漏率测试结果的关系,并给出包装箱密封性需要达到的指标;
2)包装箱内2000 Pa的初始高纯氮气会增加箱内气体的量,对总漏率检测程序中的各个相关测量值和标定过程中的放样(即式(1)中的各个参数)产生何种影响,也需要进行理论分析。
2.1 航天器包装箱本体密封性影响分析
航天器包装箱本身不是绝对密封的,各接口处和密封处均存在微小漏孔,且其内外存在2000 Pa的压差,内部气体比常压时更容易向箱外泄漏。经分析可知,包装箱在24 h内由内部泄漏至外部的气体含有部分初始空气(充入2000 Pa氮气后的混合空气)和部分航天器被测系统中泄漏出的示漏气体。
一般情况下,航天器总漏率检测时包装箱所处环境均在测试厂房内,温度可控,因此我们进行理论分析时视包装箱内温度维持恒定。建立总漏率检测系统模型:设包装箱内部容积为V1,初始阶段箱内的氦气体积分数为大气中氦的体积分数——r0=5×10-6,大气压为P0=1×105Pa,箱内初始压力P1=(105+2000) Pa。为了简化,进行理论分析时,视箱内气体泄漏到箱外的漏率为恒定的Q1,且假设气体由箱内至箱外的泄漏为等比泄漏(任意时刻泄漏出包装箱的气体中氦气体积分数等同当时箱内的氦气体积分数),航天器泄漏漏率为恒定的Q0,任意时刻t包装箱内的氦气体积分数为r,则在初始时刻,包装箱内的氦气绝对量为

随着时间的延长,航天器泄漏出的氦气会造成包装箱内部氦气绝对量的增加,而随压差由包装箱向外泄漏的气体会降低这一增量的速率[6],因此,在某一时刻t,包装箱内的氦气绝对量为
在同一时刻,包装箱内的总的气体量为

通常情况下,航天器在进行高指标检漏前已经过大漏初检,因此其泄漏量会远远小于包装箱内的总的气体量,也远远小于包装箱向外的泄漏量,因此,式(4)中的Q0t可以忽略。综上,在任意时刻t,包装箱内的氦气体积分数为

氦质谱非真空累积检漏法的测试时长为24 h,以目标灵敏度1×10-5Pa·m3/s量级作为目标值,设Q0=1×10-5Pa·m3/s;一般航天器检漏采用的包装箱内部容积在100 m3左右,因此设V1=100 m3;将P1、V1、Q0和r0的数值代入式(5)可得,当Q1=0时,即航天器包装箱完全密封的情况下,24 h后箱内的氦气体积分数r增长为 5.084 7×10-6,增长量 Δr=r−r0为 0.084 7×10-6。
由于包装箱内氦气体积分数的增长是线性的,则24 h后,泄漏出包装箱外的所有气体总和中氦气的体积分数应为24 h时箱内氦气体积分数与大气氦气体积分数之和的一半,即(r+r0)/2。基于理论分析角度,检漏结果需满足误差不大于5%,因此包装箱内氦气体积分数变化量Δr需满足95%×0.084 7×10-6≤Δr≤105%×0.0847×10-6,此时对应的Q1的最大值就是理论上容许的航天器包装箱泄漏率。
依上述数值和方法计算可得,-12.44 Pa·m3/s≤Q1≤11.22 Pa·m3/s,11.22 Pa·m3/s对应的 100 m3包装箱漏率指标为9 694 Pa/24 h,而实际包装箱正压环境下(充入2000 Pa高纯氮气)的泄漏参数均不大于300 Pa/24 h。由此可得出结论:在正压环境下利用航天器包装箱进行总漏率检测时,对检漏过程和结果造成的理论偏差影响远小于5%。
2.2 正压因素影响分析
由式(1)可知,影响航天器总漏率检测的因素主要包括:检漏仪的3个测量值(初值u1、终值u2和样值u3)以及标定过程中的取样和放样量w。u1、u2和u3是包装箱内氦气体积分数的线性反应,因此在对包装箱内充入2000 Pa高纯氮气后,这3个测量值会较常压环境下有所不同,但仅仅是绝对数值的不同,由于测试时包装箱内的环境是相同的,且航天器泄漏氦气的漏率一般是恒定的,所以,(u2−u1)和 (u3−u2)的比值在正压与常压环境下保持不变,不受2000 Pa高纯氮气的影响。对于标定过程中的取样和放样量w,通常标定采用标准容器(容积V),将其内部抽空后,充入一定压力P的氦气,之后通过循环泵放入包装箱内。但由于取样环节是在包装箱外进行,取样的压力是相对于外界大气压的压力,而包装箱内相对已经存在2000 Pa的压差,所以取样量PV放入包装箱内时,受压差影响不会完全进入箱内,实际上的放样量应为(P−2000)V,会对标定造成一定的误差。因此,实际操作中可以将标准容器的容积做得足够小(mL量级),使取样时的氦气压力P处在MPa量级,则可以将上述误差控制在1%内,从而消除其对测量的影响。
2.3 理论分析小结
综合上述理论分析可知:包装箱正压环境下氦质谱非真空累积检漏技术理论可行,在对包装箱密封性和取/放样环节进行有效控制的前提下可满足误差不大于5%的理论可行边界条件。
3 试验系统搭建及验证
将校准漏率为8.8×10-6Pa·m3/s的正压标准漏孔作为模拟被检航天器,利用最小可检漏率为1.0×10-10Pa·m3/s的检漏仪作为测试仪,用一个90 m3的刚性收集容器作为模拟包装箱(在试验前,先通过对收集容器内充入2000 Pa高纯氮气的方式测量收集容器本体的漏率为266 Pa/24 h,满足正压环境下总漏率检测条件),分别在常压和正压环境下进行总漏率检测并对比测得的数据,以验证包装箱正压环境下氦质谱非真空累积检漏技术的可行性。
化学需氧量(COD):450mg/l;生化需氧量(BOD5):200mg/l;悬浮物(SS):300mg/l;氨氮(以 N 计):35mg/l;总氮(以 N 计):50mg/l;总磷(以 P 计):5mg/l。(2)一期设计出水指标
正压和常压环境下的总漏率测量结果如表1所示。根据表1数据进行统计分析可知,正压和常压环境下测得的被测漏孔漏率均围绕真值上下波动(见图2),其中,正压环境数据组中的最大绝对误差为1.1×10-6Pa·m3/s;常压环境数据组中的最大绝对误差为 1.0×10-6Pa·m3/s,2组数据的数值和量级均相当,最大绝对误差基本相同。
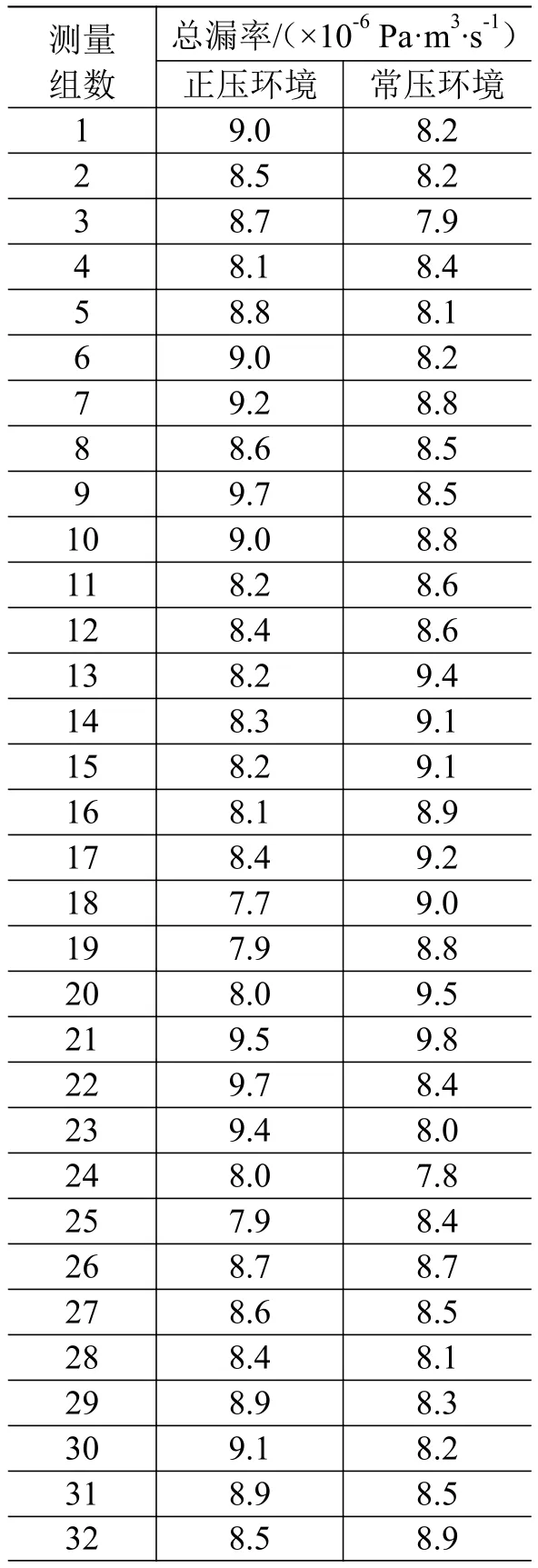
表1 总漏率检测数据对比Table 1 The leakage rate testing by different methods

图2 不同工况漏率对比Fig. 2 Leakage rate testing curves for different pressure environment
根据统计学与误差分析理论对测量数据进行分析,主要包括2组数据的均值、标准偏差、标准不确定度、相对标准不确定度、相对真值标准偏差和均值的相对误差等。具体计算公式如下:
均值为

标准偏差为

其标准不确定度为

相对标准不确定度为

相对真值标准偏差为

均值相对误差为

数据统计分析的结果见表2。2组数据相对标准不确定度均在1%左右,标准偏差均在5×10-7Pa·m3/s左右,2种方法的最大单一测量值的相对误差也均在±20%以内。根据统计学理论,可以得出结论:2组数据的精确度和准确度相当,2种工况下的总漏率测试数值误差均极小。

表2 漏率对比数组统计Table 2 The statistics of leakage test results
4 结论
本文针对常压环境下航天器总漏率检测方法中航天器包装箱无法承受负压的特种工况,提出一种基于正压环境的氦质谱累积检漏技术,并进行理论分析和试验测试。通过综合考虑计算结果和试验结果,得到以下结论:包装箱正压环境下利用氦质谱非真空累积检漏技术进行的航天器总漏率检测,相对真值标准偏差在5×10-7Pa·m3/s左右,测量漏孔漏率相对校准漏孔实际漏率值的测量最大误差在±20%以内,与目前用于航天器总漏率检测的常压环境下氦质谱非真空累积法误差相当。
综上,包装箱正压环境下航天器总漏率检测技术可行,可以满足航天器总漏率检测的需求,能够为航天器包装箱的减重设计提供参考。
