火星表面大气环境下热球风速仪的对流换热模型及试验验证

李西园，侯雅琴，高庆华，张丽娜，王 晶,3

（1. 北京卫星环境工程研究所，北京 100094； 2. 北京航空航天大学 航空科学与工程学院，北京 100191；3. 北京卫星环境工程研究所 可靠性与环境工程技术重点实验室，北京 100094）

0 引言

火星表面大气压力约为700 Pa，主要成分为CO2，温度-120～20 ℃，风速 0～15 m/s。极低气压环境下存在的对流换热使火星表面巡视器面临着与地球和一般航天器轨道空间不同的环境。为了在极端环境下达到热模型修正、早期故障筛除、性能测试等目的，火星巡视器的地面热试验一般需要极端环境叠加风速模拟[1-2]，即在中型空间环境模拟设备内部，通过调温热沉模拟冷黑背景，调温冷板模拟巡视器的地表传热，压力控制系统模拟1400 Pa左右压力环境，通过风机模拟最大15 m/s的风速，并需要对试验中的风速进行实时测量。

目前工业上常用的风速测量手段主要包括动压式、热式和超声式等。动压式风速测量主要包括风杯式、皮托管和五孔探针等形式，其中皮托管和五孔探针已经被广泛应用于低气压风速测量领域。在火星表面压力下，0～15 m/s风速带来的动压仅有0.01～10 Pa，尽管现有微压传感器产品的分辨率可以达到10-3Pa，但其体积、质量往往较大，且无法在低气压下使用，需要使用管路在容器外进行测量，而多点风速、风向的测量将会使系统变得非常复杂[3]。热式风速测量包括热线、热球和热膜等形式，其工作原理是可根据不同风速下传感器探头换热量的不同计算风速[4]。在“Netlander”“海盗号”“小猎犬二号”等火星探测器上均搭载有热式风速仪，部分还具有通过尾迹线测量风向的能力[5-6]。热式风速仪结构简单紧凑、质量小、功耗低、不需要移动部件，但其缺点也很明显：1）传感器对标定的依赖性大，无法通过分析手段获得信号−风速的关联式；2）随着时间推移，传感器阻值等特性变化会引起标定漂移；3）空气温度变化会导致信号的变化，故传感器的测量精度非常依赖于气体温度的测量。目前火星探测器使用的热式风速仪均为定制产品。超声风速测量利用了声波信号在介质中传播速度仅和气体成分及温度相关，而和压力无关的特性。相比热式风速仪，超声风速仪不需要每个都标定，其主要缺点在于超声波在低气压下衰减较大，现有产品往往很难从噪声信号中筛取超声换能器发射的信号，需要设计全新的换能器[7-8]，同时设备体积较大，难以满足多点风速测量的要求。

综上所述，目前在极低气压下，风速测量的主要途径为定制型风速传感器。本文主要针对在低气压下使用现有工业用恒热流热球风速传感器的适用性，采用无量纲数分析方法建立热球风速传感器表面的传热模型，分析传感器在不同压力下的响应特性，并搭建试验系统进行测试验证。

1 热球风速仪对流换热模型

1.1 仿真模型

热球风速探头的核心为陶瓷封装的微小球体，直径约为0.6 mm，球体内部包括热电偶的热端和加热丝，外部包括热电偶的冷端，图1所示为本文使用的热球风速探头的结构。

图1 热球风速探头结构Fig. 1 Structure of hot-bulb anemometer probe

风速测量中，加热丝上的恒定电流产生恒定的功率，此时，热电偶冷端温度可以认为是流体温度，而热端温度为热球温度。当不同速度流体流过热球表面时，对流换热系数的不同导致了球表温度的不同，继而在热电偶冷、热端之间形成热电势差；通过毫伏变送器可以对热电势差进行测量、传输，根据传感器的标定数据可换算出当前的风速。

1.2 无量纲数模型建立

传感器敏感头与周围环境的换热可以分为辐射换热、对流换热及通过引线导热3种，当忽略沿细线上的导热时，在热平衡状态下探头的加热量等于探头的对外换热量之和，

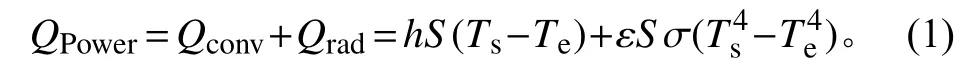
式中：Qpower为传感器敏感头热耗，W；Qconv为通过对流散失的热量，W；Qrad为通过辐射散失的热量，W；h为对流换热系数，W/(m2·K)；S为热球表面积，m2；ε为热球表面发射率；σ为斯忒藩−玻耳兹曼常量，5.67×10-8W/(m2·K4)；Ts、Te分别为热球表面温度和来流气体温度。考虑到敏感头实际与设计尺寸的偏差及引线上损失的热耗时，式(1)可表达为

式中：C1为敏感头上电阻在整个加热回路电阻中的占比；C2为敏感头实际表面积与设计表面积的比值。式(2)可以继续简化为

其中C为常数，包括了C1和C2两项常数的影响，通过数据拟合得到。

式(1)～(3)中的对流换热系数h可由努赛尔数Nu表示，

式中：λ为传热系数，W/(m·K)，随气体压力变化不大；l为特征长度，m；Nu一般可以表示为雷诺数Re的函数。球体表面流动的雷诺数可以表示为

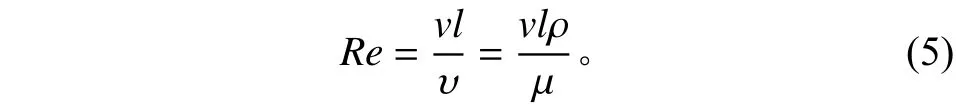
式中：v为气体流速，m/s；l为特征长度，m，取0.000 6 m；υ为气体的运动黏度，m2/s。υ随气体密度ρ变化，故将其转换为动力黏度μ和ρ的比值，其中，动力黏度μ是不随ρ变化的，气体密度ρ可由理想气体状态方程，通过气体压力、温度计算得到。根据计算，常压、0～15 m/s风速下，Re约为20～500；而在 1400 Pa环境下，Re仅为 0.1～2。针对球体表面强制对流Nu−Re经验关联式，Kramers、Whitaker、Yuge、Vilet、Raithby 等学者通过试验，给出了适用于不同范围的表达式[9]，但大多适用于中高雷诺数，在低雷诺数（0.1～10）范围偏差较大，不同经验公式间偏差可达20%[10]。根据统计，Whitaker关联式

在低雷诺数时与试验结果最为接近，其中Pr为流体普朗特数。

若式(4)～(6)中的定性温度均选取热球表面温度Ts与来流气体温度Te的平均值，传热系数λ、动力黏度μ、普朗特数Pr均表示为定性温度的函数，则当来流气体的温度、速度已知时，可通过式(4)～(6)计算敏感头表面对流换热系数h。再将各参数代入式(3)后可求解非线性方程获得热球风速传感器的表面温度。当热电偶的输出信号ΔU与温差ΔT满足ΔU=k×ΔT关系时，即可由ΔT计算得到热电偶输出信号ΔU。本文试验所用热电偶的k约为0.041 mV/℃。

1.3 自然对流与强制对流强度分析

热式风速仪传感器探头表面存在自然对流和强制对流。对于恒热流风速探头而言，自然对流随着探头的表面温度而变化，会给测量带来额外的误差，故测量时应当确保探头表面的强制对流占据主导地位。可根据无量纲数Gr/Re2来判断强制对流或自然对流的主导地位：Gr/Re2＜0.01时强制对流占据主导地位，Gr/Re2＞10时自然对流占据主导地位，Gr/Re2在0.01～10之间时则需要同时考虑这2种对流因素的影响。

式中：Gr为格拉晓夫数；g为重力加速度，m/s2；ΔT为热球与环境气体间的温差，K；av为体胀系数，K-1，其表达式为

其中：ρ为气体密度，kg/m3；P为压力，Pa；T为定性温度，K；R为摩尔气体常数。可见体胀系数与压力无关，即衡量自然对流与强制对流模式占比的无量纲数仅和重力加速度、定性温度、来流气体与热球表面的温差、特征长度、来流速度有关，其中重力加速度、特征长度、来流速度为给定值，温差可通过1.2节方法求解获得，定性温度T取来流气体与热球表面温度的平均值。

2 试验验证

2.1 试验系统及方法

为了对无量纲数模型进行验证，需要在地面建立低气压风速模拟手段。目前对于1400 Pa左右低气压下的风速模拟有旋转、闭式风洞和开式风洞3种基本方法[3]。其中旋转法的基本原理如图2所示，旋转的风速仪穿过流体，流体介质不运动，风速仪与流体介质之间存在相对运动。一般是把悬臂和转台放置于空间环境模拟容器中，容器中充入与使用环境具有相同压力、温度的气体。旋转风速模拟系统具有成本低，结构简单，容器内压力、气体成分稳定的优点。

图2 基于旋转的风速模拟系统组成Fig. 2 Wind speed simulation system based on rotation

本文基于中型空间环境模拟设备搭建了旋转风速模拟系统，见图3。热球风速探头固定于悬臂端部，已知悬臂半径和悬臂转速时可知当前风速，悬臂上安装的12位精度毫伏信号采集器可直接工作于真空环境下，采集分辨率约为0.01 mV，转换为485信号后由转台上的电刷滑环导出，并传送至容器外的计算机存储。传感器的恒定热流施加使用了容器外的程控电源，功率恒为0.08 W。

图3 风速模拟系统实物Fig. 3 Photo of the wind speed simulation system

2.2 试验结果与分析

分别对常压、4×104Pa、1400 Pa下的风速传感探头输出进行了测试。在试验中背景温度与流体温度相同，均为室温。

2.2.1 常压下

图4和图5分别为常压下输出信号与无量纲数方法预测的信号对比（其中拟合常数C≈0.067）及相应风速下的Gr/Re2，其中受限于悬臂在常压下的空气阻力，仅模拟了0～11 m/s风速下的传感器输出。由图可见，在常压下，恒热流式热球风速仪的无量纲数模型与实际输出信号的吻合度非常好，偏差在0.05 mV以内。同时，无量纲数Gr/Re2均＜0.01，即热球风速仪表面强制对流占主导地位。

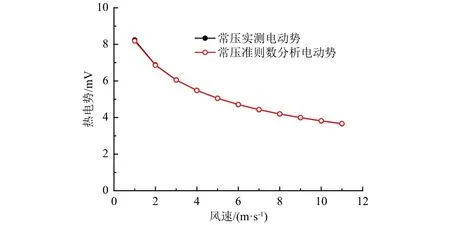
图4 常压下探头输出与无量纲分析对比Fig. 4 Comparison between probe output and dimensional analysis under ambient pressure

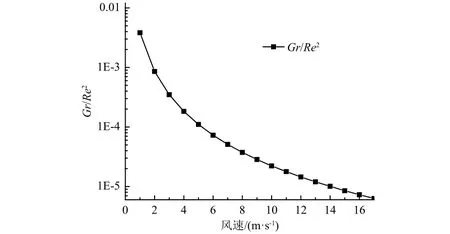
图5 常压不同风速下的Gr/Re2Fig. 5 Gr/Re2 at different wind speeds under ambient pressure

2.2.2 低压下

绘制4×104Pa、1400 Pa下传感器输出与无量纲数模型分析结果的对比（见图6）。在4×104Pa下，二者数值较为接近，但在1400 Pa压力下，分析值与试验输出存在较大的偏差，这与文献[11]中针对热线风速仪的试验结果是一致的，即在极低气压下，Nu−Re关联式会随压力的降低产生较大的偏差。因此，对于低气压下的热式风速仪的适用性研究，需要结合试验数据进行修正。

图6 4×104 Pa与1400 Pa下探头输出与无量纲分析对比Fig. 6 Comparison of probe output and Gr/Re2 analysis under pressures of 4×104 Pa and 1400 Pa

同时，由图6可见，在1400 Pa下，传感器在不同风速下的灵敏度约为0.1～0.2 mV/(m·s-1)；在低气压下进行风速测量试验时，毫伏信号的数据采集器亦应当满足相应的精度要求。此外，由于辐射换热的背景温度相关性，标定环境应该与使用环境具有接近的辐射换热背景，或在传感器表面安装高反射比的风道以降低辐射换热的影响。

根据试验结果计算热球风速探头表面的Gr/Re2，绘制1400 Pa下的Gr/Re2曲线如图7所示。当风速达到1 m/s以上时，无量纲数Gr/Re2恒＜0.01，即强制对流在总对流换热中仍占据主导地位，在这个范围内自然对流不会给测量带来额外的误差。

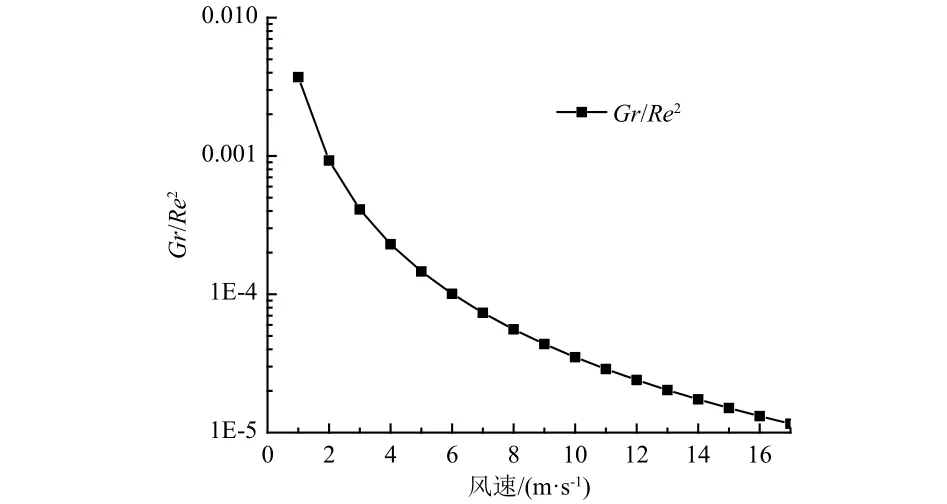
图7 1400 Pa，不同风速下的Gr/Re2Fig. 7 Gr/Re2 at different wind speeds under the pressure of 1400 Pa

3 结论

针对低气压下的风速测量问题，本文使用无量纲数分析方法建立了恒热流热球风速探头的风速−输出信号模型，基于中型空间环境模拟试验设备搭建了旋转式低气压风速标定系统，分别在常压、4×104Pa、1400 Pa的环境下进行了测试。得到了如下结论：

1）常压下的试验表明，本文建立的无量纲数分析模型与试验测试取得了一致的结果，证明了该模型对于评估传感器输出的有效性。

2）4×104Pa下的试验表明，无量纲数模型与试验结果偏差主要集中在低风速范围，在风速为2 m/s以上时，其偏差在10%以内，该模型可用于4×104Pa以上环境的热球风速传感器输出信号预测。

3）1400 Pa下的试验表明，无量纲数分析模型与试验结果存在25%左右的偏差，对于极低气压下的热球风速仪适用性分析，需要结合试验手段进行修正；同时，0.6 mm探头表面仍以强制对流换热为主，探头的灵敏度为0.1～0.2 mV/(m·s-1)，使用更高精度的采集仪器可以满足1400 Pa下的风速测量需求。