基于仿真的应急组织评价方法研究

胡冉曾斌

（海军工程大学 武汉 430034）

1 引言

应急组织是指为了保障群众生命财产安全，维护社会和谐稳定，最大限度地降低突发公共事件造成的损害而建立的统一领导组织。合理的应急组织体制是遭遇外界环境的突发事件时保证组织运行效率的基础。在信息化时代，组织结构中信息的传输与流通发生了巨大的变化，对不同组织结构进行评价，选择合理的、符合信息时代要求的应急组织结构，充分发挥组织合力，最大化实现组织在突发情况下的运行效能，具有重要的现实意义。

国内在这方面已有大量的研究，从学者来看［1］，马丽［2］以结构熵为基础，从信息的角度对组织结构有序度进行评价；代剑环［3］结合AHP、熵值法及模糊综合评价，建立组织发展评价指标体系；苏长亮［4］以熵理论为基础，提出广义信息力的概念，建立有序度评价模型。国外学者Alberts和Hayes［5］介绍了如何通过“扁平化”的分散组织来执行多单元的规划。这些研究主要以有序度熵作为组织结构评判标准，并以静态组织结构作为熵模型的输入参数，而应急组织要求对外界环境变化做出及时反应，静态的有序度熵不能有效地衡量其组织结构的适应性。

为此本文通过探讨应急组织结构中信息的传递模式，建立了阻力熵模型，并通过相应的仿真结果来计算阻力熵，从而在动态环境下评测应急组织系统。

2 阻力熵模型的建立

熵理论在信息论中它是一个随机事件不确定性的度量，对于一个广义的系统来说，熵可以作为状态的混乱性和无序性的度量。在静态环境中，通过信息的不断获取，熵总是在不断减少。

为了定义这种变化，本文将状态空间（P）划分成可行状态（Pf）和不可行状态（Pi）。在状态空间中，Brillouin［6］定义信息 I=log2||P ，且在已经接受信息Im的情况下，存在的可行性状态数量等于：

在Shannon的信息熵中，一条信息的熵等于：

那么对于一个固定不变的状态空间来说，其熵等于：

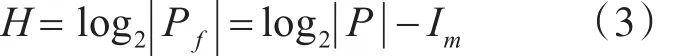
上式显示了在静态世界中熵会随着信息的获取而减小，减小的熵就等于获取信息量的大小。然而在动态环境中，信息的获取所实现的熵的减少可以被由于环境变化引起的熵增所抵消。因此，我们这里提出阻力熵的概念，用Hd表示。即由于外界环境动态变化，这种变化具有不确定性，因此熵增对组织了解环境的状态产生了阻力。由于不可行状态总是会不断转变成可行状态，而这种转变的速率便是形成阻力熵的驱动力。所以我们正式将阻力熵定义为

x表示环境在t时刻的状态。在应急组织中，时间t监测到的应急信息S的价值会随着时间的推移逐渐减少。由于应急组织存在多个监测部门且环境一直处在动态变化中，所以对于某个时间t'＞t，同一个监测部门的第二个检测值S'=(xj,t')的条件熵H(x ( t')|S)将不为零。对于在时间tk=t结束的状态x的k个信息序列S1:k={( xj,tj) }，定义系统在时间t'＞t处的观测值上的阻力熵(Hd)等于

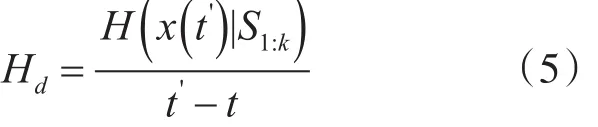
其中，H(x ( t')|S1:k)表明在已知S1:k的条件下，状态x在t'时刻的不确定性。由于阻力熵对信息的影响表现为状态空间中信息量的减少，因此信息I等于

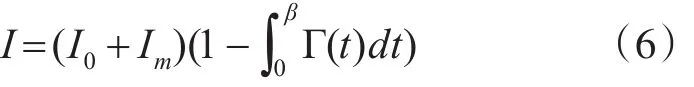
其中，β表示处理信息所需的时间，即计算复杂度。I0是开始处理之前状态空间中存在的信息内容。

3 基于仿真的阻力熵计算

3.1 信息流

为了探索信息在应急组织内的流动传输情况，本文使用几种不同拓扑结构图形G=( )V,E来模拟几种应急组织结构，每个节点v∈V代表组织内不同的部门或人员，每条边e∈E代表了两个部门或人员之间具有传输途径。仿真还在拓扑结构内定义了一组特殊的节点S⊆V，这些节点代表能够不断获取应急信息的监测部门。为了建立阻力熵的模型，本文使用了一个函数，它从to时间开始使信息逐渐发生衰减。

在这个模型中，每个部门总会处于四种状态的一种，SEND、CHECK、COMPUTE和SENSE分别代表部门发送、检查、处理和感知新信息。在SENSE状态下，监测部门i∈S读取一位无初始不确定性的信息，并在当前模拟时间将该信息与时间戳相关联。在本实验中，我们为SENSE状态分配1s的延迟。完成SENSE状态后，部门立即进入COMPUTE状态，其状态的时间长度是要处理的信息量的函数。计算延迟由与监测部门新获得的数据成正比的线性延迟决定，对每个监测部门的计数不超过一次，即只有来自给定检测部门的最近的监测值被处理。此模拟使用参数β来确定和量化处在COMPUTE状态的时间长度。COMPUTE状态完成后，部门进入SEND状态，通过发送已经处理但邻节点尚未收到的信息来与邻节点进行通信。无论发送的信息数量如何，这个通信阶段都需要设定1s的模拟时间，并且与所有的邻节点同时进行通信，而邻节点之间不存在交互。如果i∈S仍有存在数据需要处理，则从SEND状态再次进入SENSE状态，否则，进入CHECK状态。CHECK状态是一个保持状态，其一直保持到有新的信息需要接受。

3.2 控制流

为了模拟各部门在信息交互时的指令与信息流之间的关系，这就限制了组织必须是树型的层次结构，即每一级子部门都从属于上一级部门，每一级的部门都能够处理从下层部门传上来的信息，同时根据信息控制下级的行为。

在这次仿真中，每个部门在任意时间点都处在七个状态中之一：SENSE，SEND_I，REC_I，PROC，SEND_A，REC_A，ACT和HOLD。与上一个相同，监测部门获取一位的信息。如果该部门没有子部门，则该部门在一个单位时间内转成HOLD状态，并尝试与上一级部门进行通信，否则，就转入PROC状态。在SEND_I状态，部门将其从子部门收到的所有检测值发送到上一级部门，而上一级部门必须处在REC_I状态。SEND_I状态结束后，部门将进入PROC状态，而REC_I状态结束后，如果是根节点，并且收到其所有子部门的信息，则将进入PROC。与之对应的是SEND_A和REC_A。在SEND_A状态，上级部门将控制命令传递给所有的监测部门，而接受命令的监测部门必须处在REC_A状态。SEND_A结束后，部门进入HOLD状态；REC_A结束后，如果该部门是监测部门，则转入ACT状态，否则同样进入HOLD。在PROC状态，部门将对其所有子部门增加一个时间步长的延迟，用来表示每个监测的一个时间步长的处理延迟。PROC结束后，监测部门会进入ACT状态，而其他部门则进入HOLD状态。ACT状态需要一个时间步长来表示将控制命令应用监测部门，并且如果部门仍有控制命令需要传递给子部门，则该转换为HOLD，否则，转变为SENSE。在HOLD状态下，上级部门首先在其子部门中查找也处于HOLD状态但尚未接收到其最近控制命令的部门。如果存在这样的子部门，则子部门转换到REC_A，该部门转换到SEND_A。如果没有，且自上一次与上级部门通讯以来，已经获得了子部门的所有信息，那么该部门将向其上一级部门尝试通信，如果是这种情况，则该部门转换到SEND_I，上级部门转换到REC_I。如果上述两个步骤均不导致状态转换，则将保持HOLD状态，直到下一个时间再次尝试通信。

与上一个仿真不同，这次每个部门一次只能同一个邻接部门进行通讯，并且必须等待邻居准备好发起通信。此次仿真中监测部门的数量仍是64个，但部门总数是不同的，从而探求部门数对应急组织结构的影响，且用于评价的指标不再是信息量，而是控制信息的总和。

4 仿真结果及分析

为了验证某些网络拓扑结构在不同阻力熵和复杂度条件下比其他网络拓扑结构表现更好的假设，我们比较了衰减-复杂度(Γ ，β)在5个不同图形中的模拟情况。本实验包含了一个完全连通图，一个二叉树、一个4元树、一个小世界图和一个无标度图。所有模拟的应急组织都有127个部门，其中64个为监测部门。在模拟开始时，每个监测部门只执行一次监测。在本次仿真中使用的主要度量是在给定时间步骤内处理的所有监测信息的总和，其用来表示处理后的信息量。本节以表格的形式给出两种仿真结果。其中表1～5反映的是五种拓扑结构在不同条件下处理信息量的数量。图1反映的是多种树形层次结构在不同阻力熵下产生的控制信息数量。

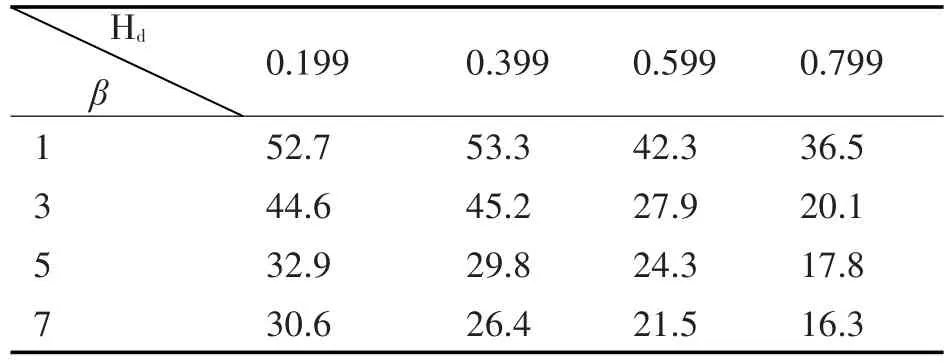
表1 完全图信息量计算结果

表2 二叉树信息量计算结果

表3 （3，3）无标度图信息量计算结果

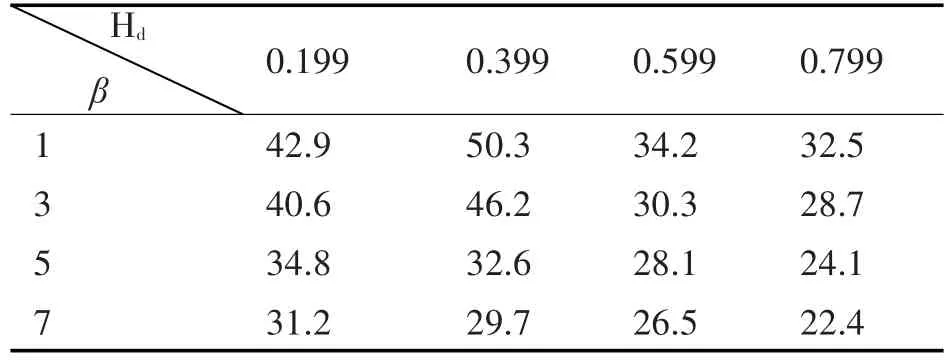
表4 3环+10信息量计算结果

表5 4元树信息量计算结果

由上表可见，当计算复杂度小于1时，完全图结构在任意衰减度下都能处理较多的信息；当计算复杂度在（3，5）区间，阻力熵（0.599，0.799）时，3环+10图可以处理较多的信息；而二叉树和（3，3）无标度图总体而言信息量大小相似，不同情况下相差不大；4元树相较于其他四种结构则表现情况较差。

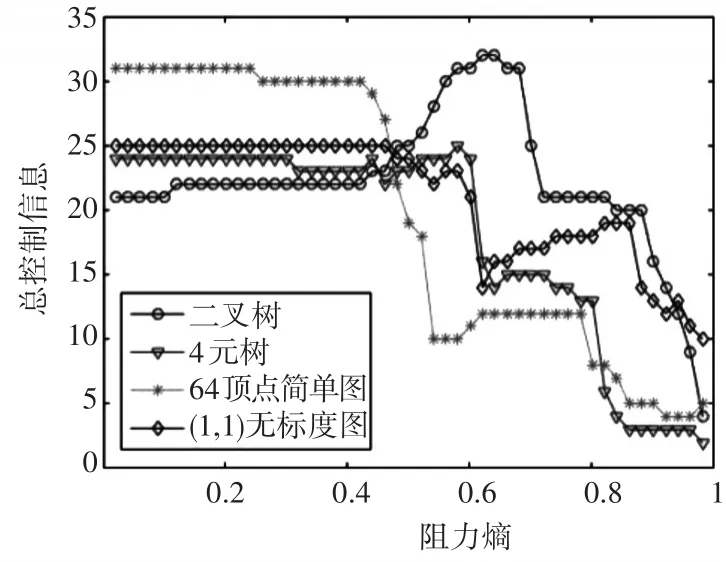
图1 总控制信息量随延迟率的变化

图1 表明，在阻力熵较低时，简单连接且部门数较少的组织结构由于信息传输效率较高，控制信息基于从下层传输的信息较多，从而产生的控制信息也较多，相反的情况发生在阻力熵较高的区域。随着阻力熵的增加，二叉树结构相对于其他拓扑结构总控制信息大幅明显增加。在阻力熵较高的区域，无标度图明显优于其他三种结构。

由仿真结果可见，以完全图结构构成的应急组织在监测到的信息所需计算量较小时，可以有效及时地处理和交互组织获得的信息，然而当阻力熵较高时，各个监测部门信息计算时间过长，导致组织无法及时处理所有的信息，从而造成信息的迟滞和堆积，严重影响应急组织在处突时的效率。像无标度图和二叉树这样的层次结构，在具有一定阻力熵和复杂度的情况下，仍能够较好地处理组织内的信息，但在复杂度较高时，这两种结构都不如小世界网络结构。而类似4元树的层次组织结构因为组织过于冗余，在任何情况下处理信息的能力都不如其他组织结构。

5 结语

本文介绍了一种基于信息论的组织结构评估方法。具体而言，用复杂性和阻力熵来表征组织结构的性能。结果表明，信息量与组织结构确实存在相关性。在实验中发现，用于描述场景的最佳信息量和该场景中用于协调操作的最佳拓扑结构随着场景的信息量度变化而变化。特别是，对于某些信息的特征，二叉树结构优于无尺度的拓扑结构。基于这些结果，我们可以说，一个应急组织用来影响指挥和控制的结构应该随着情况的变化而变化，而信息理论指标可以用作选择组织结构的标准。