战场侦察数据在频域上的异常分析

叶青张剑

（武汉数字工程研究所 武汉 430205）

1 引言

随着军队信息化程度的不断提高，各种武器装备、通信系统、指挥控制系统、情报处理系统都向数字化方式转变，指挥员将面对全方位、多兵种、复杂环境下的高科技战争［1］。因此，如何处理大量战场信息，给指挥员提供可靠、有用的战场信息，帮助指挥员进行正确、有效的决策，成为取得战场优势的关键［2］。从信息优势转化为决策优势进而提高战斗力，就需要对战场信息进行快速、精准的处理。

2 侦察数据在频域上的异常分析

2.1 异常分析的意义

战场上在长期对远距离域进行观察和监控后，获得了大量的数据，通过对这些数据的分析处理可以形成一种易于指挥员理解并能辅助其决策的电磁环境的表达方式。它包括辐射源目标态势、装备用频状态、电磁环境信息，它们可以为电子对抗、频谱管控、航路规划等指控功能提供准确的数据支撑，同时能为指挥员提供丰富且便于理解的信息表现形式，使其更好地认清和理解战场电磁环境［3］。

在现代战争中，电磁频谱是极其重要的战争资源，它影响甚至决定着战争的进程和结局。电磁频谱是电磁信号在频域的表现形态，它将信号在时间域中的波形转变为频率域的频谱，进而可以对信号的信息作定量解释［4］。电磁频谱是唯一能支持机动作战、分散作战和高强度作战的重要媒质，被称为与地面、海洋、空间和太空并存的第五维战场，所以，对战场进行频域分析是十分必要的［5］。为了能够及时准确地发现战场上地方电磁环境的突发变化并进行分析处理，达到预警敌方战略的变化效果，就需要对电磁频谱数据的异常变化进行分析。

本文选取通过侦察获取到的数据中的战场固定区域内十一个频段上目标数量的变化进行异常分析。

2.2 异常数据监测算法

聚类分析是一种重要的异常数据检测方法，它利用相似性度量，把样本集组织成若干个有意义的子集，相似度较高的样本归为一类，相似度较小或不相似的样本则在不同的类中［6］。通过这样的划分，可战场固定区域内十一个频段上目标数量样本集中的正常数据和异常数据区分开来。当前的聚类算法大多采用距离作为样本间的相似性度量，这是一种样本间的模糊关系、反映样本间的相似程度［7］。

经典的K均值聚类算法采用欧式距离度量不同样本间的相似程度。一般来说，对于两个n维向量X和Y，用欧式距离计算它们的距离：

但是，欧氏距离将样本的不同属性（即各指标或各变量）之间的差别等同对待，算法对于向量不同下标之间的关联性和相似性没有考虑，这一点有时不能满足实际要求。因为对于一个目标的频段变化，跨度大与跨度小所代表的实际意义，是有很大差别的，而通过欧式距离所算出的结果是一致的，这就导致结果产生了很大的偏差［8］。所以，针对上述缺点，本文对K-means聚类算法进行改进，将欧氏距离用二次型距离替代，以适应我们所研究的场景。

2.2.1 K-means聚类算法

K-means算法又叫K-平均或K均值算法，是一种使用最广泛的聚类算法。它将各个聚类子集内的所有数据样本的均值作为该聚类的代表点，算法的主要思想是通过迭代过程把数据集划分为不同的类别，使得评价聚类性能的测度函数达到最优，从而使生成的每个聚类内紧凑，聚类间独立［9］。

算法的计算流程：首先从n个数据对象任意选择k个对象作为初始聚类中心；而对于所剩下其它对象，则根据它们与这些聚类中心的相似度（距离），分别将它们分配给与其最相似的（聚类中心所代表的）聚类；然后再计算每个所获新聚类的聚类中心（该聚类中所有对象的均值）；不断重复这一过程直到标准测度函数开始收敛为止。一般都采用均方差作为标准测度函数［10］。

2.2.2 基于二次型距离的K-means聚类算法

二次型距离源于统计学领域的Mahalanobis距离［11］，其计算公式为

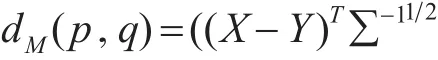
其中，X和Y为两个n维向量，∑为向量各元素之间距离的协方差矩阵，要求逆矩阵存在。我们通常利用一个相关矩阵A来取代∑的逆矩阵，来反映向量中各元素之间的相关程度。A中的元素计算如下：

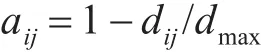
其中，dij为直方图第i个子区间与第j个子区间之间的空间距离，即dij= ||i-j，dmax=max(dij)，此时，上式变为二次型距离的标准形式：

特别的，当相似度矩阵为n阶单位矩阵时，二次型距离即转化为欧氏距离的平方，因为此时除对角线外的元素均为零，即不存在元素之间的相似性关系。

根据十一个频段（HF，VHF，UHF，L，S，C，X，Ku，K，Ka，mm）的分类构造相似性矩阵：

这种计算方式考虑了直方图元素之间的相似性，可以让结果更符合我们对直方图距离的直观感受。

2.3 异常值检测

2.3.1 选取数据集

为了判断所要检测的当天数据是否异常，我们需要可以参照的数据来进行对比，也就是历史数据。但是历史数据每天不断产生，比较庞杂，这些数据中大多为正常数据，但是也可能存在异常数据，所以需要先将这些数据进行处理，筛选出可用于训练的数据。此时采用基于二次型距离的K-MEANS聚类算法，得到可用的数据集。

由于战场的形势是在不断变化的，选取过长的时间周期的数据进行处理可能产生较大的误差，所以我们将待检测数据前30天的数据作为一个周期。为了提高对比数据的合理性，将一天24小时的数据分为12段，统计从0点开始，每两个小时段中各个频段中的目标数量，将这30个数据作为一组数据集，从而得到一共12组数据集。

2.3.2 数据处理

通过基于二次型距离的K-MEANS聚类算法分别处理这12组数据。

在处理之前，需要先选取k值。针对K-means聚类算法需要事先给出k的初始值这一问题，考虑到只需要区分数据是否为异常，故可以将k的值固定设为2，仅将数据划分为正常聚类和异常聚类。这样既解决了每次执行算法都要进行赋值的麻烦，又避免了算法重复执行来选取最优k值时不必要的时间花销，从而简化算法，减少能量消耗，提高效率。

然后开始数据处理。

第一步：通过改进后的K-means聚类算法进行分簇，分簇之后，得到正常值簇和异常值簇两个簇，获取正常值簇的簇心C。

第二步：计算所有数据与正常值簇的簇心之间的二次型距离：

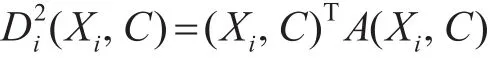
其中，Xi表示第i个数据。

第三步，计算平均距离：

其中n表示数据的总数。

第四步：比较数据集中所有数据与簇心之间的二次型距离，若某个数据与簇心之间的二次型距离大于当前的平均距离，即

那么将该数据点归入疑似异常点集。

第五步：计算该聚类内全部数据点到簇心距离标准差：

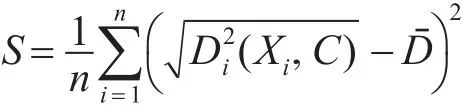
第六步：比较所有疑似异常点到簇心的距离跟平均距离之差与该聚类内全部数据点到簇心距离标准差S的1.67倍（取置信区间为90%），如果大于后者，即

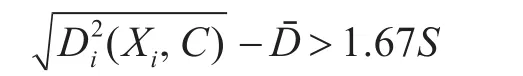
则认为该数据为异常数据［12］。

第七步：检测待测数据是否为异常值。计算待测数据与正常值簇心之间的二次型距离，根据第四步、第五步和第六步的步骤，判断此待测数据是否异常。

3 仿真分析

本文所有实验均在Matlab平台上进行。

设定在一个固定域内，将连续30天的侦察数据分12组共360个样本数据通过2.3.2节所述方法进行处理，仿真结果如表1所示。

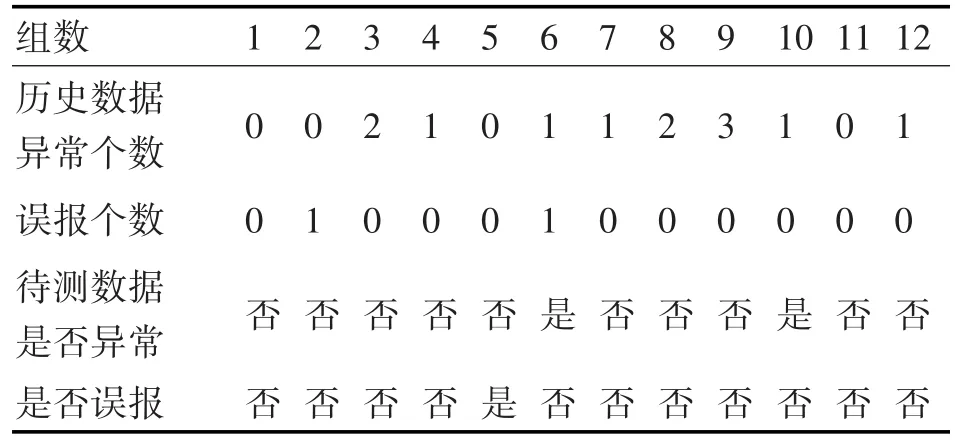
表1 仿真结果

仿真结果符合预期，说明通过本文所述方法，良好地分析出战场固定区域内24小时各个时间段中各频段上目标数量变化的异常情况。

4 结语

针对战场在对远距离域进行观察和监控后，获得大量数据在频域上的异常数据分析处理问题，提出了一种将二次型距离与K-means聚类算法相结合的改进的K-means聚类算法以适用于我们所研究的场景。该方法表明通过数据分析计算后，良好地分析出战场固定区域内24小时各个时间段中各频段上目标数量变化的异常情况，以达到预警的效果。然而在样本数量较大时，聚类计算速度受到影响。因此如何改进计算方法以提高计算速度和减小误差，今后仍应该继续深入研究。