基于时频联合的信号检测算法性能分析及应用
2018-10-23李越岭丁兆贵
李越岭 丁兆贵
(中国船舶重工集团公司第七二三研究所 扬州 225101)
1 引言
现代复杂电子环境中,雷达信号往往淹没在各类噪声中,这增大了传统电子侦察设备对其检测的难度,因此如何在强噪声背景中有效检测出微弱雷达信号已经成为现今电子战重要研究课题之一[1]。
经典和常用的雷达信号检测方法一般有时域相关检测算法和基于频域的FFT算法。时域相关检测算法可实时处理雷达信号,但对雷达信号的信噪比要求较高,当信噪比下降时系统的检测性能会急剧下降,很难保证较高的检测概率;频域FFT算法进行FFT运算,不仅无法准确判断雷达信号的起始和结束时刻,而且也无法保证信号的实时检测要求,而到达时间和脉冲宽度这两个参数对于未知雷达信号的识别和分选具有重要的意义[2~3]。因此,必须采用一些新技术和新方法来改善检测系统的输入信噪比,然后再利用改进的检测算法在强噪声背景中提取出有用信号,从而完成低信噪比环境下的信号检测。
本文介绍的低信噪比检测算法是将频域FFT算法和自相关算法结合起来的一种联合信号检测算法,在低信噪比情况下,能以较大概率检测到信号,并能精确地估计出信号的起始时刻和脉冲的宽度,最终将截获数据送往后续的信号处理,进行雷达信号脉内和脉间分析。
2 低信噪比信号检测的理论分析
2.1 窗函数的设计及加窗前后性能比较
在工程中,对雷达信号进行加窗是有效提高信噪比的处理方式。因为实际环境中雷达信号是非平稳的,直接用单个离散傅里叶变换在频域中对整个雷达信号进行描述会产生错误的结果,因此为了得到雷达信号参数的时变本质,可以将整个信号长序列分割成多组较短的信号子序列,每个信号子序列以均匀时间间隔为中心,并分别计算其DFT,这样可以将非平稳信号等效为平稳信号进行处理。为了用一组短信号序列表示非平稳信号x(n),可以将其与一个相对于时间平稳的窗w(n)相乘,并将信号移过该窗,通过加窗得到的子序列的离散时间傅里叶变换称为短时傅里叶变换(STFT)[4]。这里窗函数采用最大平坦窗[5~6]:
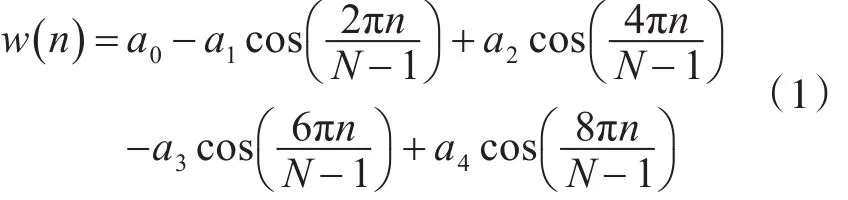
其中 0≤n≤N-1,权重系数如表1所示。
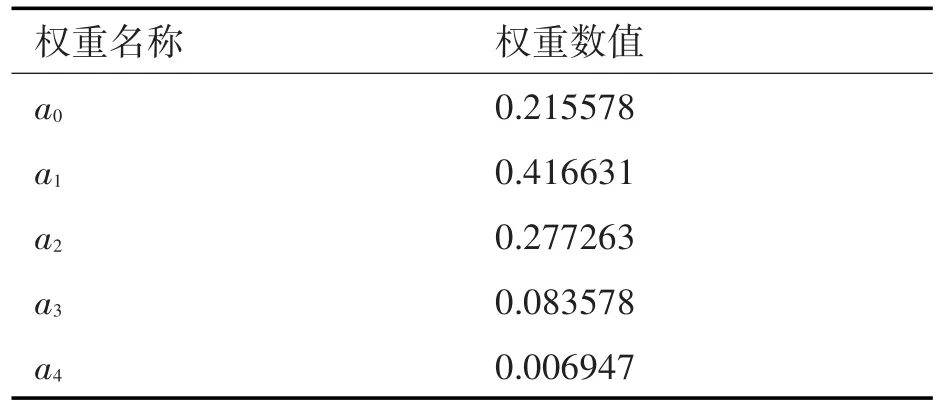
表1 权重系数
最大平坦窗的时频特性曲线如图1所示。

图1 最大平坦窗时频特性曲线
对于短时傅里叶变换(Short Time Fourier Transform,STFT),由于存在时间上的截断,通过加窗可以降低截断带来的影响[7]:

至此,完成加窗操作。图2给出信号加窗前后的对比结果。
从图2可以看出,加窗之后尽管增加了信号频域宽度,但加窗有效抑制其他杂散频点的幅度,进一步降低频域信号的噪底,提高信噪比,从而进一步提升信号检测性能。
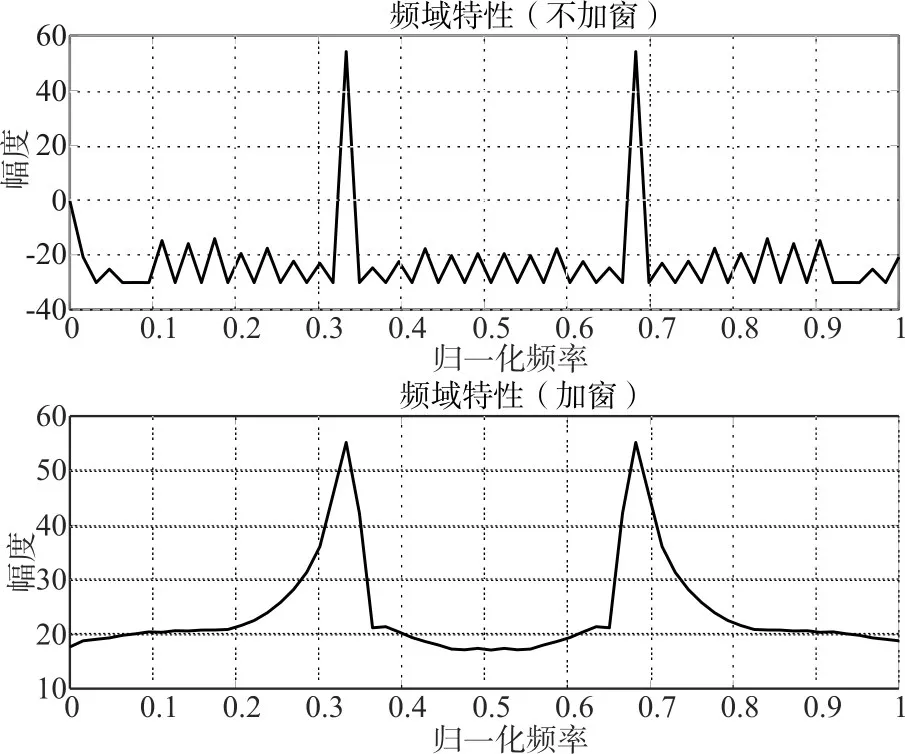
图2 加窗前后频域性能对比
2.2 自相关检测联合的信号检测方法
给出自相关的定义式:
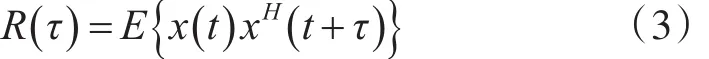
在实际工程应用中,假设信号满足独立同分布,且符合遍历性假设,则自相关表达式可近似表述为[8]
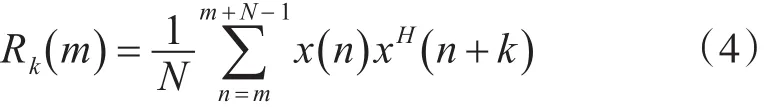
其中k表示相关函数的时间间隔,m表示起始时刻,N表示截取的时间片。令
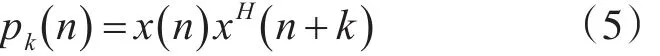
则将pk(n)看作系统输入,Rk(m)看作系统输出,则利用z变换可求出系统响应函数:
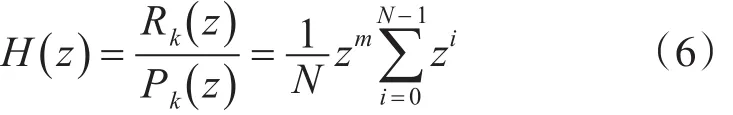
式(6)描述了累加估计自相关函数的系统,式(6)可进一步写为
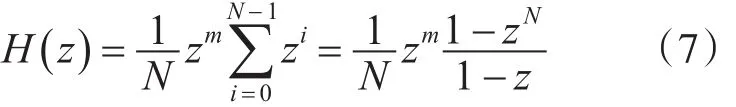
式(7)描述了系统的简化模型:递归模型。将系统响应函数映射到时域,得到
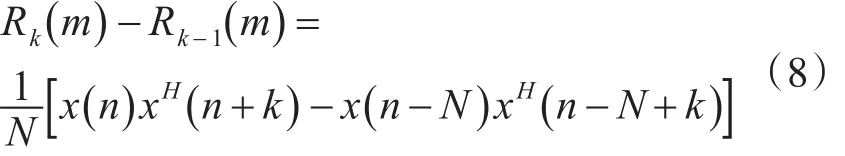
若在工程中采用式(8)的思路进行硬件实现,可进一步降低硬件资源。
2.3 仿真分析
假设信号频率为268.75MHz,信号采样率为400MHz,对应信噪比为SNR=0dB,噪声为高斯白噪声。信号时域波形如图3所示。

图3 原始时域信号波形
传统信号检测,主要在时域进行,图4分别给出时域信号的幅度、自相关之后的幅度。
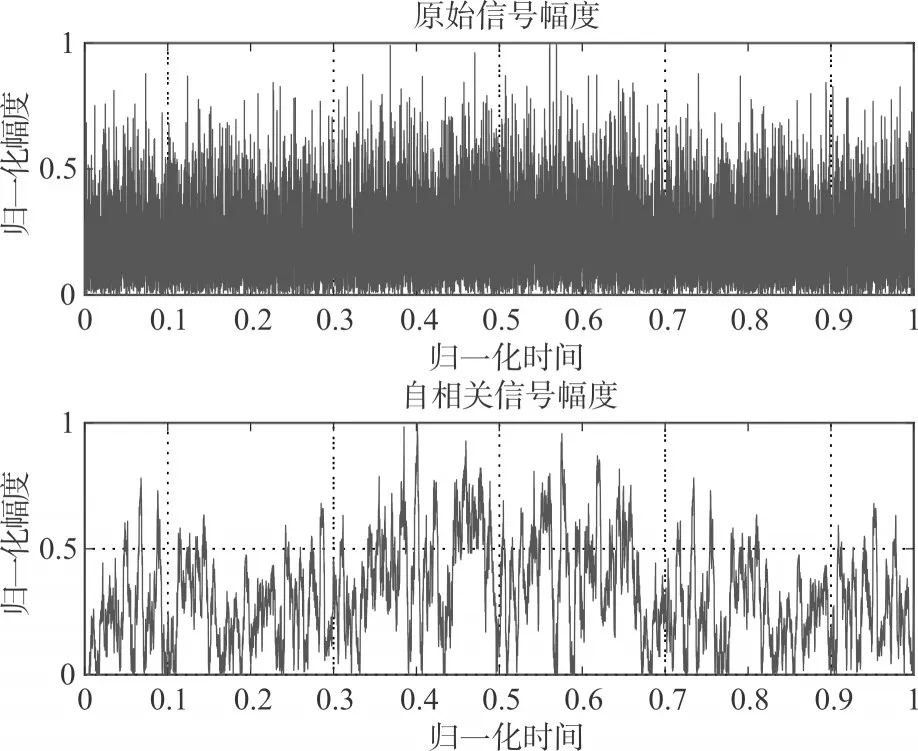
图4 时域自相关前后幅度对比图
从图4可以看出,即使对时域信号进行自相关操作,仍然难以完成信号的有效检测。
现在考虑对信号进行短时傅里叶变换,并检测有效信号频点,提取频域信号。图5给出频域幅度、自相关之后幅度的对比图。
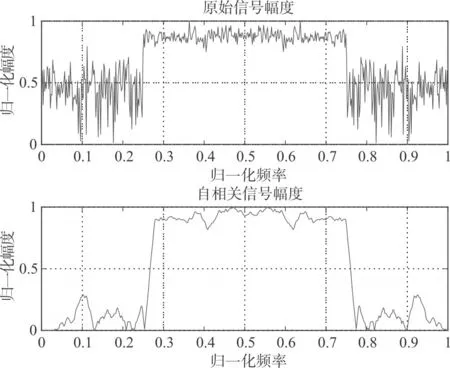
图5 频域自相关前后幅度对比图
分析图5可以看出,频域变换之后信号与噪声有效分离开来,对其进行自相关处理后,信噪比得到了进一步的提升,仿真结果与理论分析一致:频域处理借助了时间的积累特性,在平稳信号环境下,信噪比得到了进一步的提升,从而改善了信号检测的性能[9]。
3 低信噪比信号检测算法的工程实现
3.1 低信噪比信号检测算法的整体架构设计
本文阐述的应用中,数字接收机采样中频带宽100MHz,根据带通采样原理选择4倍带宽的采样时钟[10]。硬件平台中ADC对信号采样后,以400Mbps的数据率传输到FPGA中,FPGA采用多路并行接收的方式将采样数据全部接收后进行流水处理,后端处理整体设计方案如图6所示。
在图中算法首先实现64点FFT处理,为了匹配输入信号数据率和FFT核的处理速率,将信号经过32点滑窗分为4次FFT处理,具体做法是:第0~31点加窗后数据作为第一次FFT的输入,并使用第1个FFT核进行FFT计算,同理,第16~47点加窗后数据是第二次FFT输入,第32~63点加窗后数据是第三次FFT输入,第48~63和下一个第0~15点作为第四次FFT输入。当下一次的第0~31点时,复用第一次第0~31点的加窗结果,并使用第5个FFT核进行FFT处理,依次类推[11~12]。
在完成16个FFT之后,每个FFT的结果自相关处理,最后融合18个检测抽头的检测结果,并将得到的自相关值提取出来。

图6 信号检测整体设计框图
3.2 低信噪比信号检测算法的各模块单元设计
本文阐述的信号检测算法主要包括窗函数单元、FFT单元、相关检测单元、融合选择单元等。窗函数单元主要有窗函数系数设计、加窗运算的实现;FFT单元例化IP核进行FFT运算;相关检测单元主要完成延时相乘、信号积分运算、门限判决;融合选择单元选择过门限通道,提取相关值。
3.2.1 窗函数单元设计
窗函数单元设计主要包含窗函数系数设计、加窗运算。窗函数系数根据式(1)的描述,加窗运算的结构及其实现如图7、图8所示。具体做法是:在计算前将生成的192个抽头系数抽头系数存入FPGA的ROM中,在加窗运算时从ROM中读取窗系数,再与输入的AD数据相乘,根据加窗实现框图对相乘的数据进行延时相加,最后将得到的加窗数据输出,输出公式如下:

其中n取值范围为0~63。
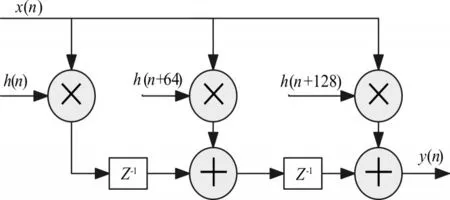
图7 加窗结构图
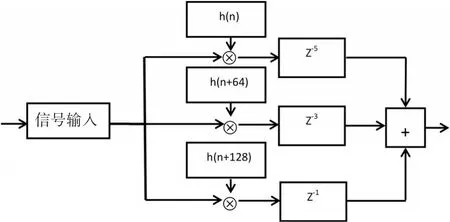
图8 加窗实现框图
3.2.2 FFT单元设计
本设计中输入信号数据点的长度确定为64点,要求以50%的重叠方式对数据点进行FFT运算,即32点滑窗处理。当工作时钟为200MHz时,每16个时钟进行一次FFT运算,时间为80ns,运算16次FFT的总时间为1.28μs,也就是252个时钟周期。使用双通道FFT IP CORE,从开始输入数据到计算结束并完全输出的时间为1.31μs。经过仿真后,从开始输入数据到再次可接收数据的时间约为0.96μs,也就是191个时间周期,仿真后可满足每32个时钟进行一次FFT运算的设计要求,在200MHz工作时钟下,基4的64点FFT核需使用17个DSP资源,FFT核主要参数及资源评估如表2所示[13]。
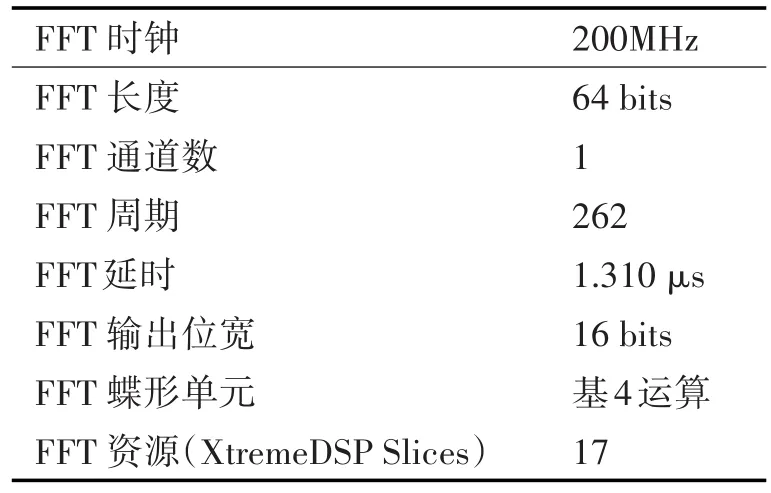
表2 FFT参数及资源评估
3.2.3 相关检测单元设计
对于自相关的硬件实现,这里仍然采用传统的乘加操作,而未利用上文递归实现,理论上二者效果完全等价。相关检测单元主要分三个小模块:
1)延时相乘模块:对输入的信号根据设置的延迟值进行延迟并取共轭,使用复数乘法器进行相乘;
2)积分模块:每16个数据为一组进行相加,再根据配置要求输出相应的积分值;
3)门限判决:将积分输出值取模与双门限值比较,得到检测结果。
延时相乘实现框图及积分实现模块如图9、图10所示,积分长度选择范围如表3所示,可实现16至128级积分可选,本系统采用8个16级积分级联,可根据外部配置命令选择输出。

图10 积分模块实现框图
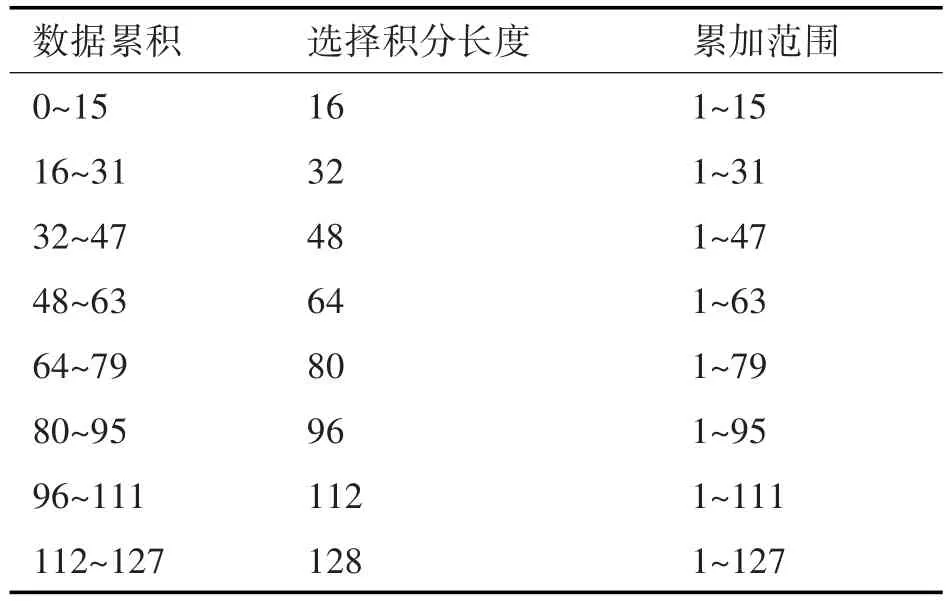
表3 积分选择范围
3.3 工程测试结果
使用本设计中时频联合检测算法,在接收机输入信噪比为-6dBc的情况下,能够有效检测出脉冲宽度在10μs以上的信号,并在某工程样机上得到验证。
4 结语
本文在某工程背景下,提出一种时频联合的检测算法,此算法能够在低信噪比条件下检测出强噪声中的弱雷达信号,并在FPGA中验证了本算法,这为进一步分析和处理此类信号提供了依据,有助于进一步研究。
