典型载波恢复盲均衡算法比较研究

叶利民 宁小玲

（1.海军工程大学研究生院 武汉 430033）（2.海军工程大学兵器工程学院 武汉 430033）

1 引言

不需训练序列的盲均衡算法是一种克服多途效应的有效方法，适用于带宽资源受限的水声信道，近年来一直是研究的热点［1］。传统的CMA算法性能稳定且容易实现，但CMA旨在使幅度代价函数最小化，当有相位错误时，CMA算法也会收敛，却无法完成载波恢复，需经过额外的相位恢复过程来纠正相位误差［2］。文献［3］中提出的修正的常数模算法（MCMA）可在一定程度上进行载波相位补偿，但是MCMA算法还是存在稳态误差大、收敛速度等问题。文献［4］提出了适用于高阶QAM信号的水声信道修正盲均衡算法（Improved MCMA），该算法通过对均衡器权值迭代函数进行修改，从而修正误差控制信号，有效减小对高阶信号的剩余均方误差，提高收敛速度，从而提高水声通信质量。超指数迭代（SEI）算法因具有快速收敛性能而受到重视，为了提高SEI算法的收敛性能和克服相位旋转，文献［5］提出了一种修正的超指数迭代双模盲均衡算法（MSEI+DD）。文献［6］提出了一种改进超指数迭代判决反馈盲均衡算法。该算法基于对修正超指数迭代算法（MSEI）误差函数的分析，提出了一种新的、能够快速收敛的误差函数，并有效提高相位补偿能力。为了进一步提高算法在复杂水声信道的载波恢复和收敛性能，文献［7］提出了一种基于正方形判决带二阶锁相环的修正超指数迭代判决反馈盲均衡算法（SDSEI-DFE-2DPLL）。

本文就均衡输出图、MSE性能分别比较了以上几种载波恢复盲均衡算法的均衡性能。

2 算法原理

盲均衡算法通常分为三大类：Bussgang类盲均衡算法、高阶统计量类盲均衡算法以及非线性均衡器盲均衡算法。其中，Bussgang类盲均衡算法中研究较为广泛的是常数模算法（Constant Modulus Algorithm，CMA），该算法代价函数仅与接收信号的幅值有关，而与相位无关，故不能进行载波恢复［8］。所以，修正的CMA算法（Modified CMA，MCMA）算法得到研究，它对于常模信号或非常信号都具有良好的收敛能力。

2.1 Bussgang类盲均衡算法

盲均衡算法的基带模型图如1所示。

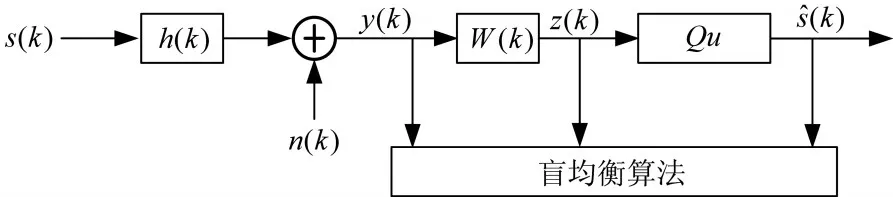
图1 盲均衡算法的基带模型图

CMA算法：

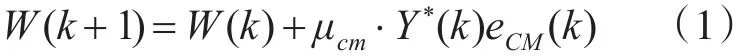
其中：

针对CMA算法存在无法完成载波恢复的问题，文献［3］讨论了一种修正的CMA算法（简称MCMA）。该算法将CM代价函数分为实部和虚部两个部分，对接收信号实、虚部分别处理，提出了一种多模准则，产生了下面的随机梯度算法。

MCMA算法：

其中，下标R、I分别表示相应的实部、虚部分量。算法最常用的 p=2。当 p≥4时，MCMA算法展现出很差的收敛性能。p=2时得到误差函数为

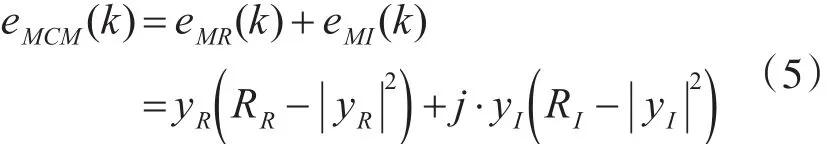
式中：

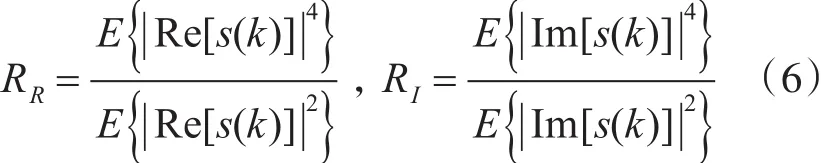
当 p≥4时，MCMA算法展现出很差的收敛性能，这是因为对于一个很小的 y，上式的误差函数变得很小，接近于零，这时算法不能收敛［9］。文献［4］提出了一种适用于高阶QAM信号的水声信道修正盲均衡算法（Improved MCMA）。Improved MCMA算法将CM代价函数分为实部和虚部两个部分，对接收信号实、虚部分别处理，提出了一种多模准则，产生了下面的随机梯度算法：

Improved MCMA算法：

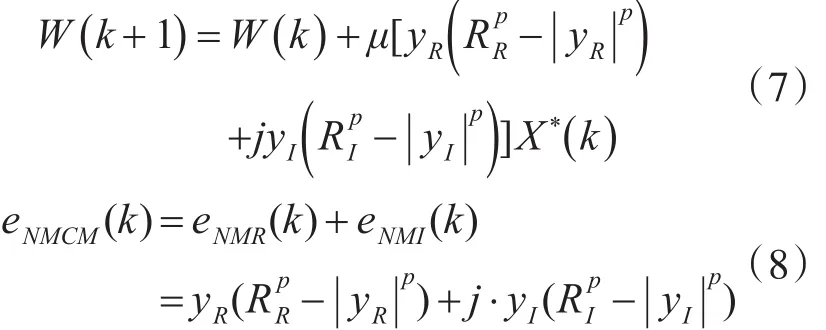
式中：

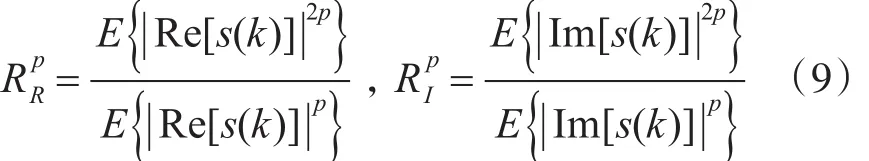
Improved MCMA作为盲均衡算法，不需占用带宽资源，计算量小，且具有和LMS算法相当的收敛性能。

一个普遍的均衡器策略是判决反馈均衡器（Decision-Feedback Equalizer，DFE），在信道失真严重的情况下，DFE因其具有非常良好的时变跟踪性能而被广泛采用［10～11］。所以，在本文的仿真试验中，均采用了基于DFE的均衡算法。

DFE算法的等效基带模型如图2所示。

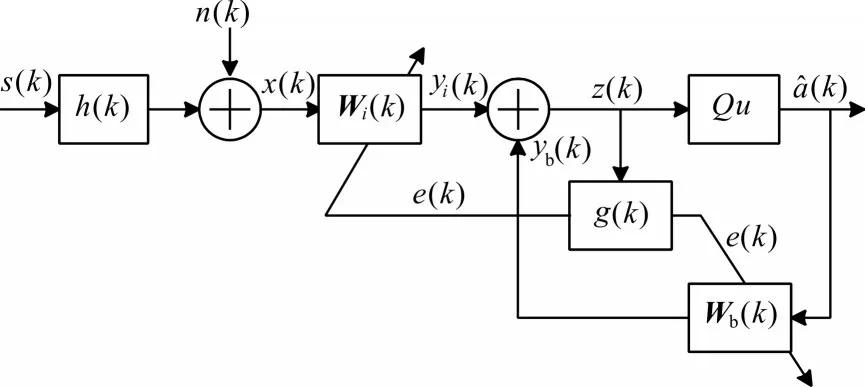
图2 判决反馈均衡器示意图

2.2 高阶统计量类盲均衡算法

基于高阶统计量的盲均衡算法中典型的算法有超指数（Super-Exponential Iteration，SEI）算法，该算法因具有近乎于超指数的收敛速度而在高速的水声通信中得到广泛应用。

SEI算法是在CMA算法上提出来的，由于CMA对相位是盲的，因此，SEI对相位也是盲的，当存在载波相位残余时，剩余的相位起伏会使得均衡器输出星座产生旋转。文献［6］通过借鉴MCMA算法的误差函数，对均衡器输出的实部和虚部分别采用非线性变换，获得一种修正的超指数迭代算法（NMSEI），加快收敛速度，并减小剩余均方误差。

NMSEI-DFE算法：

μ1和 μ2分别表示前向权和反馈权的迭代步长。Q矩阵因子的迭代方程为

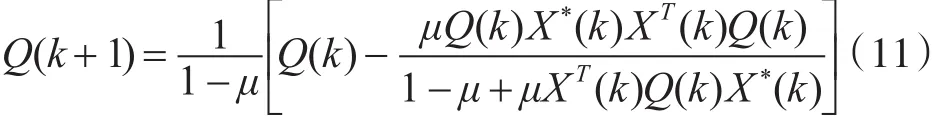
算法的误差项为

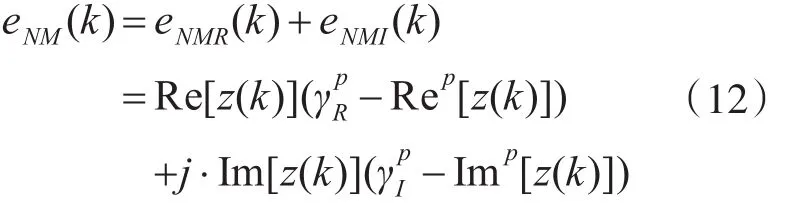
式中：

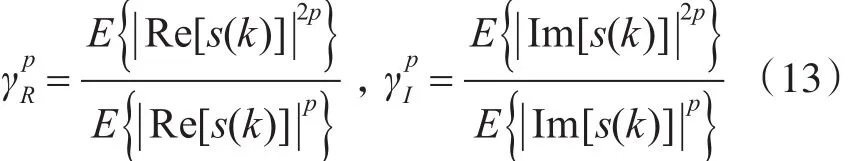
算法最常用的 p=2时，NMSEI-DFE算法为常见的修正超指数迭代算法（MSEI）。MSEI-DFE算法的误差项为

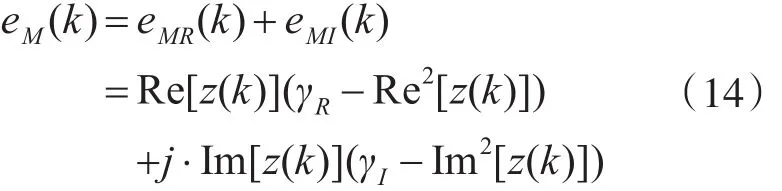
式中：

尽管MSEI算法在载波恢复性能上通过将误差函数分为实部和虚部2个部分，对算法进行了改进，但是，当算法应用于非常模信号（如16QAM）通信系统时，误差信号在任何一个信号点处都不会趋于零，从而使得算法的起伏性较大，收敛速度较慢。为了提高收敛性能，增强算法稳健性，文献［7］提出了Improved MSEI-DFE-DD算法，在收敛阶段采用MSEI-DFE算法，之后根据某一切换准则，切换到基于DD的判决反馈算法。算法的切换门限为M0，判决误差为 De(k)= | z(k)-aˆ(k)| ，具体的操作过程为

当De(k)≤M0时，判决反馈器权向量的迭代过程转换为

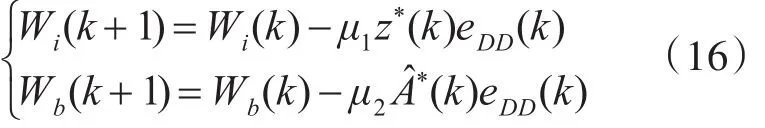
这时，DD算法误差为

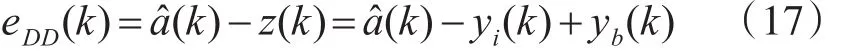
3 算法性能比较与分析

为了检验各种算法在混合相位系统中载波恢复性能，以CMA-DFE、MCMA-DFE、Improved MCMA-DFE、SEI-DFE、MSEI-DFE、NMSEI-DFE 以及NMSEI-DFE-DD算法进行比较。利用文献［12］的深海信道模型进行仿真，基带水声信道冲激响应为 c1= ［0.2443， 0.1183，-0.0455，-0.0905，0.6766，0.6622，-0.1163，0.0756］，该信道的零点分布如图3所示。

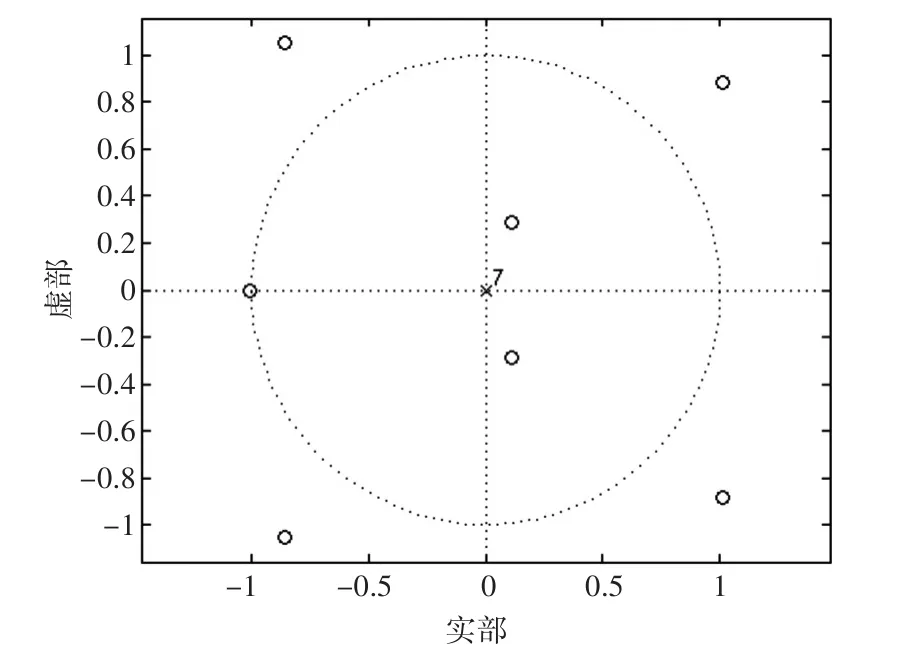
图3 信道的零极点图

由图3可见该信道是一个混合相位系统，有一零点十分接近单位圆，形成了很深的谱零点，因此，其均衡难度较大。在整个仿真过程中，判决反馈均衡器前向权采用中心抽头初始化，而对反馈权采用全零初始化，前馈滤波器权向量长为15，反馈滤波器权向量长为8。Q矩阵的初始值为均衡器一段输入数据的相关矩阵的逆：Q(0)=R-1，矩阵的大小为512。各种算法的参数均设置为：μ=0.001，μ1=0.001，μ2=0.001。

图4给出了在QPSK调制信号、高斯白噪声信噪比SNR=30dB的情况下，各种算法的MSE曲线。从图4（a）可以看出：SEI算法因具有快速收敛性，SEI-DFE算法相比CMA-DFE、MCMA-DFE以及Improved MCMA-DFE的收敛速度快约2000点；而MCMA-DFE和Improved MCMA-DFE相比没有相位纠正的CMA-DFE、SEI-DFE算法，其收敛后的稳态误差要小8 dB。这直接证实图4（b）中文献［6］NMSEI-DFE算法的相位补偿能力和快速收敛性能。

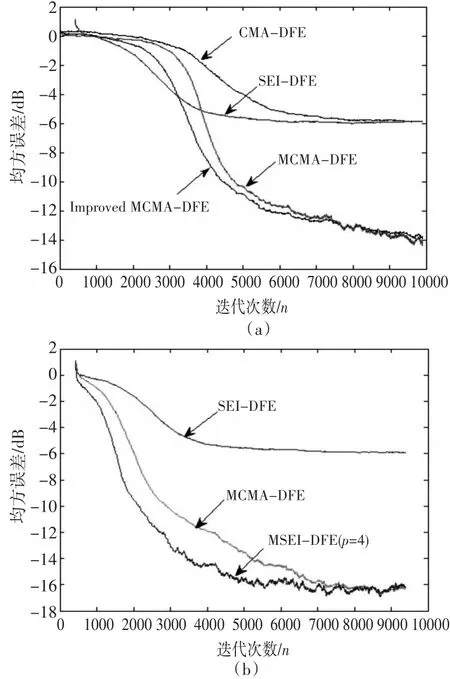
图4 各算法的MSE性能比较（SNR=30dB，QPSK调制信号）

图5 各算法的MSE性能比较（SNR=20dB，16QAM调制信号）

图5 给出了在16QAM调制信号、高斯白噪声信噪比SNR=20dB的情况下，各种算法的MSE曲线。从图5（a）、图5（b）可以看出：采用不同调制信号时，各算法的性能差异呈现相同的特性。采用相位纠正的SEI算法具有更好的收敛性能，且Improved MCMA-DFE和NMSEI-DFE类算法收敛后的稳态误差相同。

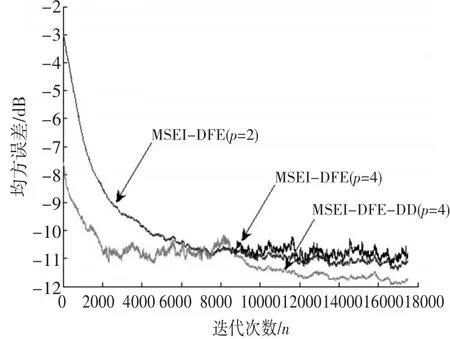
图6 各算法的MSE性能比较（SNR=20dB，QPSK调制信号）

图6 给出了在QPSK调制信号、高斯白噪声信噪比SNR=20dB的情况下，各种算法的MSE曲线。NMSEI-DFE-DD算法是NMSEI-DFE和文献［7］MSEI-DFE-DD算法的结合，在MSEI-DFE-DD算法的基础上提高算法收敛后的稳定性，改善算法的稳态误差性能。从图6可以看出，NMSEI-DFE-DD相比NMSEI-DFE算法的稳态误差小1 dB，且收敛后算法MSE曲线明显稳定一些。

4 结语

论文采用混合相位信道模型、两种调制方式（QPSK和16QAM）对基于DFE结构的典型的Bussgang类盲均衡算法和高阶统计量类盲均衡算法进行了性能比较，鉴于以上各种判决反馈算法在采用不同调制方式下的性能比较，可以得到这样的结论：

1）修正的常数模算法和超指数算法对相位的补偿，相比常数模算法和超指数算法，增强稳态误差和加快收敛；

2）具有载波恢复能力的NMSEI类算法和MCMA类算法收敛后具有相同的稳态误差，但NMSEI类算法收敛速度更快；

3）收敛阶段采用MSEI类算法，收敛稳定后采用判决误差准则切换至DD算法，有助于提高算法收敛后的稳定性，改善算法的稳态误差性能。