惯性原件随机噪声卡尔曼滤波器设计

2018-10-23季凯源熊天武

舰船电子对抗 2018年4期

季凯源,熊天武

(中国船舶重工集团公司第七二三研究所,江苏扬州225101)

0 引言

雷达稳定平台伺服控制中经常采用惯性测量元件(如加速度计、陀螺仪)对平台的姿态信息进行检测,但由于成本以及加工工艺等原因,惯性测量元件的测量精度并不完全满足要求,需要进行数据滤波与补偿。数字滤波无需硬件,采用算法实现,具有可靠性高且通过适当改变滤波算法参数即能调整滤波特性的优点。利用Allan方差法[1]对陀螺仪信号噪声进行分析,主要为零偏不稳定性和速率随机游走噪声等随机误差成分。随机误差常用的滤波方式[2-6]有中值滤波、均值滤波、卡尔曼滤波等。中值滤波与均值滤波不能有效处理参数快速变化的被测量。本文设计基于ARMA模型的卡尔曼滤波器对惯性测量元件信号进行处理,抑制噪声干扰,提高测量精度。

1 卡尔曼滤波基本原理

卡尔曼滤波是一系列递归数学公式的描述,以最小均方误差作为估计最佳准则,提供一种高效可计算的方法来估计过程的状态[7]。

对于离散系统,线性状态方程可以描述为:

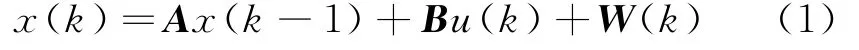
系统实际测量值:

利用系统模型,预测下一时刻系统状态:

卡尔曼滤波包括预估与校正两部分,预估是指根据模型建立当前时刻状态的先验估计,推算当前时刻状态变量及误差协方差的估计值,为下一时刻状态构建先验估计值;校正是指利用预估过程得到的先验估计值对当前时刻测量值进行最优估计,得到最优的滤波值。卡尔曼滤波器设计过程中模型的选取与建立以及模型的精度是关键,直接影响滤波效果[8-12]。

2 ARMA模型

ARMA模型是时间序列分析的一种重要方法,以AR模型(自回归模型)与MA模型(滑动平均模型)为基础构成。

式中:p、q为模型阶次;φt、θt为模型系数。

建立ARMA模型需要随机时间序列是平稳、零均值的,所以对静态的陀螺仪测量信号要进行预处理,去除野值和趋势项,进行平稳性检验、正态性检验,保证该时间序列为平稳的零均值序列,然后再建立模型。

(1)去除趋势项和野值

数据采集过程中,可能是数据采集、传输故障产生的错误数据,部分测量值明显区别于其他数据,需要剔除。

(2)随机误差建模

一个平稳、正态分布的随机序列可以用ARMA(p,q)模型表示:

式中:εi～W(0,σ2);ai＜1(i=1,2,…,p),为自回归系数;bi＜1(i=1,2,…,q),为自回归滑动系数;W(0,σ2)表示均值为零、方差为σ2的离散白噪声序列。

(3)模型阶次确定

ARMA模型阶次选择,采用Box和Jenkins提出的利用序列自相关系数函数与偏相关系数函数方法进行定阶。图1为陀螺仪信号时间序列的自相关系数和非相关性系数函数列表。图1中上下2条横线分别表示自相关系数、偏相关系数的上下界,超出边界的部分表示存在相关关系。

图1 时间序列自相关、偏相关性分析

由图1可知,AR阶次低于3阶,MA阶次低于4阶。因为对于实际随机系统,ARMA模型中AR阶次大于等于 MA阶次,可得模型为AR(1)、AR(2)、ARMA(1,1)、ARMA(2,1)。

利用Eviews软件对各阶次ARMA模型的参数进行计算以及有效性检验,模型参数及检验结果见表1。表中系数有效性检验认为小于5%为系数显著,越小越好;AIC和SBC是选择模型的重要指标,数值越小越好。由表1可以看出,不同阶次的模型AIC与SBC参数有细微差别,但并无本质变化,说明几种阶次的模型精度相差不大。就实际情况而言,模型阶次越低,实现越简单,故此选择AR(1)模型。

表1 模型阶次及其有效性检验

3 基于ARMA模型的卡尔曼滤波器设计

根据Nyquist采样定理,采样频率至少是传感器带宽的2倍才能保证采集信息不失真[15]。对于Allan方差处理,文献[15]提出采样频率至少为陀螺仪带宽的3～6倍才能保证数据处理的准确性。陀螺仪嵌在稳定平台内部,尽量保证在旋转过程中,稳定平台与陀螺仪同轴,这样可以减少系统误差。陀螺仪带宽为40～140 Hz可调,考虑到转速环实际控制周期(1 ms),故采样频率选择2 k Hz,采样时间5小时,静态、动态数据均为实验室室温下采集。

参考相关文献[16]以及陀螺仪数据分析结果,卡尔曼滤波器主要参数选择如表2所示。图2、图3为基于AR(1)模型的卡尔曼滤波实现的滤波效果。

表2 滤波器主要参数

图2中原始数据为实验室室温下陀螺仪静态数据,噪声主要为随机噪声,图2(a)为原始信号与滤波后信号对比图,图2(b)为滤波前后频谱分析对比图,图2(c)为滤波前后Allan方差分析对比图,表3为滤波前后陀螺仪信号噪声系数Allan分析结果。通过滤波前后频谱图、Allan方差分析结果对比均可以看出噪声幅值明显下降,卡尔曼滤波能够较好地滤除陀螺信号中的随机干扰噪声。